Исследовательская работа "Математические аспекты в экологии"

Районная учебно-исследовательская  конференция «Старт в науку»

 

 

Математические аспекты в экологии

Исследовательская работа

 

 

Работу выполнила

Ученица11 класса

Никитченко Инна

 

Руководитель  Баймуканова

Гульнара Тлеуовна

 

                                                  

 

 

 

МБОУ «Юбилейная СОШ»

2015 год

 

Содержание

 

I.Введение

II.Состояние лесов России

III.Математические понятия

Площадь поверхности и объём прямоугольного параллелепипеда

Понятие производной

Задачи оптимизации

IV.Практическая часть

Исследование 1

Исследование 2

Исследование 3

Исследование 4

Анализ  полученных результатов

V.Заключение

Используемая литература

 

 

 

 

 

 

 

 

 

 

 

 

 

I.                  Введение

В последнее время тревогу вызывает состояние лесов России. Они занимают 45 % площади страны и выполняют исключительно важные почвозащитные, водоохранные и климатообразующие функции. В последние годы средства массовой информации, как оппозиционные, так и официальные, публикуют большое количество материалов о лесных пожарах и массовых незаконных вырубках. Негативные последствия уничтожения лесов будут ощущаться на протяжении многих десятилетий. И тем не менее государство не предпринимает мер по выявлению первопричин сложившейся ситуации и кардинальному улучшению охраны лесов.   

В связи с этим возникает острая необходимость решать вопросы рационального использования лесного фонда Земли. Поэтому данная тема исследования является актуальной.

В данной работе раскрыты вопросы состояния лесов в России  и один из возможных путей экономии лесных ресурсов при изготовлении упаковочного материала для чая. При нахождении оптимальных размеров коробок были использованы такие математические понятия как площадь поверхности и объем параллелепипеда, производная функции и задачи оптимизации.      Для исследования были взяты три упаковки  отечественного производителя  от чая «МК», 100г, «Липтон»,100г и «Принцесса Нури».

Перед исследованием был проведен опрос среди учеников  5, 7 и 8 классов. Нужно было ответить на вопросы «Знаете ли вы, откуда берётся материал для изготовления коробок для чая?» и «Знаете ли вы, что с помощью математики можно найти  такие оптимальные размеры коробок, которые позволят сохранить огромный запас древесного материала?». Результаты опроса представлены на диаграммах 1 и 2.

 

 

 

 Вопрос: «Знаете ли Вы, откуда берётся материал для изготовления коробок для чая?»

 

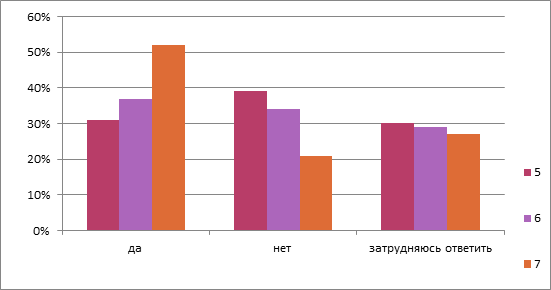
2                   Вопрос: «Знаете ли вы, что с помощью математики можно найти  такие оптимальные размеры коробок, которые позволят сохранить огромный запас древесного материала?»

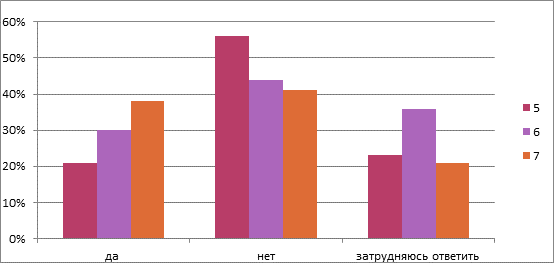
На основании данных опроса можно сделать вывод о том, что большая часть опрошенных сомневаются в том, что с помощью математических расчетов можно сохранить природные ресурсы.

 

Гипотеза:

Действительно ли, что с помощью математики можно подобрать оптимальные размеры коробки.

 

Цель исследования:

Рассмотреть способы нахождения  оптимальных размеров для экономичной упаковки.

 

Задачи работы:

·        Изучить состояние лесов в Росси;

·        Раскрыть математические понятия объема и поверхности прямоугольного параллелепипеда, производной функции и задачи оптимизации.

·        Рассмотреть различные способы экономии затратного материала.

·        Проанализировать полученные результаты вычислений.

 

Объект исследования:

Вопросы экономии и математические понятия объёма, площади поверхности прямоугольного параллелепипеда, производной функции.

 

Предмет исследования:

Упаковки чая «МК», «Липтон», «Принцесса Нури»

Методы исследования:

·        изучение литературы;

·        анкетирование;

·        математическая обработка данных;

·        измерение, вычисление, сравнение и анализ результатов;

·        прогнозирование

·         

II.              Состояние лесов России

Россия обладает самыми большими в мире запасами леса и лесными площадями. На 1993 г. примерная площадь (данные земельного лесного учетов расходятся) покрытых лесом земель составляла около 800 млн.га, а общий запас древесины - 80.7 млрд. куб.м., что составляет соответственно 21.7 и 25.9%% мировых запасов. Превышение второй цифры над первой говорит о том, что Россия располагает более зрелыми и более продуктивными лесами, чем остальные страны мира На нашей территории находится более 26% неосвоенных лесных экосистем мира, благодаря которым в решающей степени обеспечивается устойчивость биосферы и климата планеты и, соответственно, благополучие всех расположенных на ней стран, государств и народов.

Признание мировым сообществом глобальной опасности перехода биосферы в неустойчивое состояние вылилось в заключение соглашений по регулированию выброса парниковых газов.

Вырубка лесов влияет на экологическую обстановку. Особенно это наблюдается в центре Европейской России, в Поволжье и Волго-Вятском районе (см.Рис.).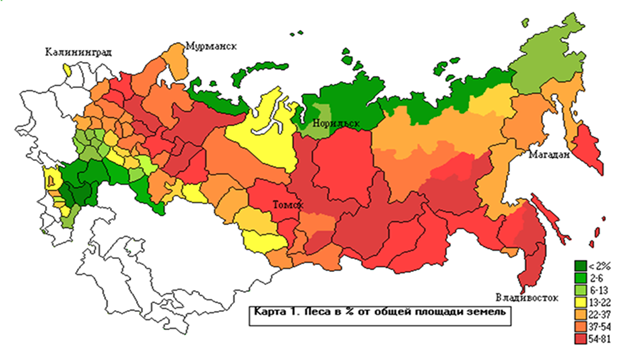

Аномальные погодные условия во многих регионах России и пожары явились причиной гибели лесов на площади 1,3 млн га, однако последствия этих воздействий будут проявляться еще в течение нескольких лет.

 

Сокращение площади лесов.

 

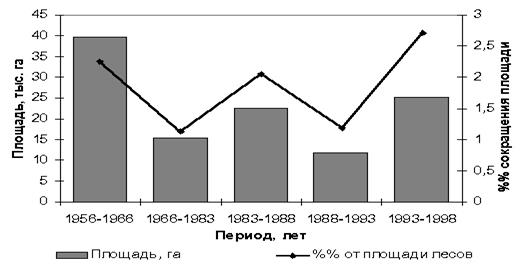
В целях рационального использования  лесных ресурсов можно рассмотрим способ экономии расходного материала при изготовлении упаковок для чая, которые имеют форму прямоугольного параллелепипеда. Такие задачи называются задачами оптимизации, которые решаются с помощью некоторых математических понятий. 

 

III.      Математические понятия

 

Площадь поверхности и объем прямоугольного параллелепипеда

Параллелепипедом называется призма, основание которой параллелограмм. Параллелепипед имеет шесть граней, и все они — параллелограммы. Параллелепипед, четыре боковые грани которого — прямоугольники, называется прямым. Прямой параллелепипед, у которого все шесть граней прямоугольники, называется прямоугольным. Площадь поверхности прямоугольного параллелепипеда равна удвоенной сумме площадей трех граней этого параллелепипеда:

S=2(Sa+Sb+Sc)= 2(ab+ bc+ ac)

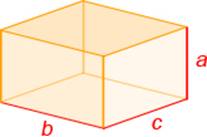(a,b,c - ребра параллелепипеда)

 

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:V= SH= abc(H - высота параллелепипеда, a,b,c - ребра параллелепипеда)

 

Пример 1. (задача из сайта Дмитрия Гущина «Решу ЕГЭ» /http://reshuege.ru) Два ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 2 и 6. Объем па­рал­ле­ле­пи­пе­да равен 48. Най­ди­те тре­тье ребро па­рал­ле­ле­пи­пе­да, вы­хо­дя­щее из той же вер­ши­ны.

Ре­ше­ние.

Объем пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да равен про­из­ве­де­нию его из­ме­ре­ний. По­это­му, если x — ис­ко­мое ребро, то 2  6  x = 48, от­ку­да x = 4.

Ответ: 4.

 

Пример 2. (задача из сайта Дмитрия Гущина «Решу ЕГЭ» /http://reshuege.ru) Два ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 3 и 4. Пло­щадь по­верх­но­сти этого па­рал­ле­ле­пи­пе­да равна 94. Най­ди­те тре­тье ребро, вы­хо­дя­щее из той же вер­ши­ны.

Ре­ше­ние.

Обо­зна­чим из­вест­ные ребра за  и , а не­из­вест­ное за . Пло­щадь по­верх­но­сти па­рал­ле­ле­пи­пе­да вы­ра­жа­ет­ся как . Вы­ра­зим : , от­ку­да не­из­вест­ное ребро

 

.

Ответ: 5.

 

 

 

Понятие производной.

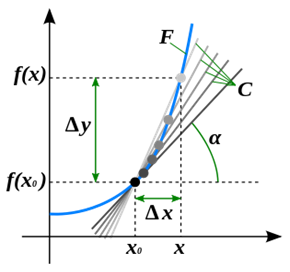
Иллюстрация понятия производной

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

Производная чаще всего определяется через понятия теории пределов.

Производной функции  в точке  называется предел отношения  приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

 

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая. Расстояние Δx = x — x₀устремляется к нулю, в результате секущая переходит в касательную. Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Физический смысл производной. Пусть  — закон прямолинейного движения. Тогда  выражает мгновенную скорость движения в момент времени  Вторая производная выражает мгновенное ускорение в момент времени

Вообще производная функции  в точке  выражает скорость изменения функции в точке , то есть скорость протекания процесса, описанного зависимостью 

 

Задачи оптимизации.

Способы экономии расходного материала решаются с помощью задач оптимизации. Задачи оптимизации - это задачи получения заданного результата при наименьших затратных средств и материалов, или при заданных исходных данных получить наилучший результат.

Например:

Задача №1. Открытый бак с квадратным основанием должен вмещать 32 л воды. При каких размерах на его изготовление уйдет наименьшее количество материала?

Задача №2. Определить размер прямоугольного бассейна данного объема V и глубиной Н, чтобы на его облицовку потребовалось наименьшее количество материала.

Задача №3. При проектировании цеха по переработке плодоовощной продукции планируется строительство нескольких холодильных камер, каждая из которых имеет форму правильной четырехугольной призмы объемом 144 м³. Для облицовки боковых стенок камеры используют материал, цена которого 15 д. е., а для облицовки дна – 20 д. е. за 1 м². При каких размерах холодильной камеры стоимость ее облицовки будет наименьшей?

 

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке [a;b]

1.     Находим область определения функции и проверяем, содержится ли в ней весь отрезок [a;b].

2.     Находим все точки, в которых не существует первая производная и которые содержатся в отрезке [a;b] (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.

3.     Определяем все стационарные точки, попадающие в отрезок [a;b]. Для этого,находим производную функции, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.

4.     Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b.

5.     Из полученных значений функции выбираем наибольшее и наименьшее - они и будут искомыми наибольшим и наименьшим значениями функции соответственно.

 

Решение задачи №1: Пусть a-длинна, b-высота, c-ширина. Объём бака можно вычислить по формуле V= abc, а так как в основании бака находится квадрат, то из этого следует, что длина равна высоте (a=c), то объём бака можно найти так: V=a²b=32

Площадь поверхности открытого бака находится по формуле

S=a²+4ab, где b=32/a² (из формулы V=a²b=32), тогдаS=a²+4×32×a/a²=a²+128/a

S'=2a+(-128/a²)=2a-128/a²

2a-128/a²=0

2a³=128

a³=64

a=4

Сделав проверку знаков производной, убеждаемся в том, что 4 является наименьшим числом.

 

 

 

a=4, из уравнения 4²+b=32находим b: b=2, а c=a=4

Ответ: оптимальные размеры бака 4×4×2  (дм)

 

IV.           Практическая часть

Рассмотрим три коробочки для чая «Липтон»,  «МК, «Принцесса Нури» (100 г). Данные упаковки изготовлены в России.

Я считаю, что если уменьшить расход материала за счет уменьшения размеров коробки, при сохранении объема,  то можно сэкономить расходные материалы.

 

Исследование 1.Измерение ребер коробок, вычисление их объемов и площадей поверхностей.

1)    Упаковка чая «Липтон»,  100 г.

Размеры в см: 10,3×7,6×4,5 без учета припусков на швы.

V₁=352,26 см³

^S₁=2(10,3×7.6+10,3×4,5+7,6×4,5)=317,26 (см²)

2)    Упаковка чая «МК», 100 г.

Размеры в см: 11,6×8,8×3,2  без учета припусков на швы.

V₂=326,656 см³

S₂=2(11,6×8,8+11,6×3,2+8,8×3,2)=334,72(см²)

3)    Упаковка чая «Принцесса Нури», 100 г.

Размеры в см: 11×7,6×4 без учета припусков на швы.

V₃=334,4 см³

S₃=2(11×7,6+11×4+7,6×4)=316 (см²)

Исследование 2. Сравнительный анализ полученных данных.

 

 

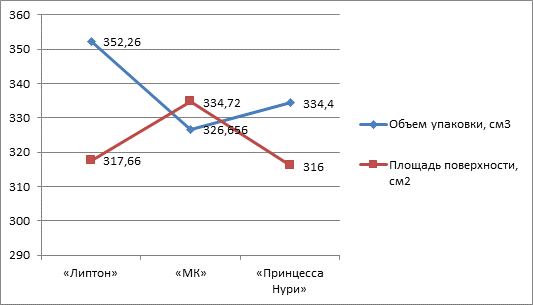
Из графика видно, что наиболее экономичная упаковка от чая «Липтон», так как при наибольшем объеме площадь ее поверхности принимает значение не наибольшее.

Таким образом,  из трех представленных коробок размеры коробки «Липтон» самые экономичные.

 

 

Исследование 3. Вычисление оптимальных размеров для новой упаковки (без использования понятия «производная»).

Найдём отношение наибольшего объема (упаковка «Липтон») к наименьшему (упаковка «МК»).

V₁ /V₂=1,08

Уменьшим поочередно каждую из сторон упаковки «Липтон» в 1,08 раз и вычислим площадь поверхности:

1)    4,5:1,08 = 4,2

получим размеры: 10,3×7,6×4,2

S=2(10,3×7,6 + 7,6×4,2 + 10,3×4,2)=306 (см²)

 

2)    10,3:1,08 = 9,5

получим размеры: 9,5×7,6×4,5

S =2(9,5×7,6 + 7,6×4,5 + 4,5×9,5) =298,3(см²)

 

3)    7,6:1,08 = 7,04

получим размеры: 10,3×7,04×4,5

S = 2(9,5×7,6 + 7,04×4,5 + 4,5×9,5) = 293,26(см²)

 

И так, мы получили при минимально допустимом объеме наименьшая площадь  поверхности упаковки 293,26 см². То есть на 1 коробке можно сэкономить до 24,4 см²расходного материала (317,66 -293,26 = 24,4).

 

Исследование 4.Вычисление оптимальных размеров для новой упаковки с помощью производной (задача на оптимизацию).

1)                    Вычислим значение наименьшей площади коробки «Липтон» при заданном ее объёме 352,26см³.

Возьмём коробку с формой прямоугольного параллелепипеда, в основании которого находится квадрат.

Пусть a-ширина, b-высота, c-длина, тогда

V=abc=352,26; a=c

V=a²b=352,26. Отсюдавыражаемb: b=352.26/a²

Площадь полной поверхности прямоугольного параллелепипеда можно найти по формуле S=2а²+4аb.

Подставляем переменную b, выраженную через объём в уравнение:

S=2а²+4а*(352,26/а²)=2а²+1409,04/а

Далее находим производную от площади и приравняем ее к нулю:

S'=4а+(-1409,04/а²)=4а-1409,04/а²; 4а-1409,04/а²=0

4а³=1409,04

а ³=352,26

а=7,07

Проверяем знаки производной и с помощью прямой убеждаемся, чтоа = 7,07

является наименьшим числом

 

 

 

Подставляем a в выражение b=352.26/a², и вычисляем b:

b =7,05

Подставим данные значения в формулу площади и получим

S=299,34 см².

 

Таким образом, мы получили до 18,32 см²экономии материала с 1 коробки, но при условии, что основание коробки квадратное.

2)           Вычислим значение наименьшей площади поверхности коробки«МК» при  наименьшем заданном ее объёме 326,656 см³.

Возьмём коробку с формой прямоугольного параллелепипеда, в основании которого находится квадрат.

Пусть a-ширина, b-высота, c-длина, тогда

V=abc=326,656; a=c

V=a²b=326,656. Отсюда выражаем b: b=326,656/a²

Площадь полной поверхности прямоугольного параллелепипеда можно найти по формуле S=2а²+4аb.

Подставляем переменную b, выраженную через объём в уравнение:

S=2а²+4а*(326,26/а²)=2а²+1306,624/а

Далее находим производную от площади и приравняем ее к нулю:

S'=4а+(-1306,624/а²)=4а-1306,624/а²; 4а-1306,624/а² = 0

4а³= 1306,624

а ³= 326,26

а= 6,887

Проверяем знаки производной и с помощью прямой убеждаемся что, а = 6,887 является наименьшим числом

 

 

 

Подставляем a в выражение b= 326,656/a², и вычисляем b:

b =6,887

Подставим данные значения в формулу площади и получим

S= 284,58 см².

 

Мы получили до 50,14 см²экономии материала с одной коробки, но при условии, что основание коробки квадратное.

3)                Вычислим значение наименьшей площади поверхности коробки при заданном объёме 334,4см³(«Принцесса Нури»).

Возьмём коробку с формой прямоугольного параллелепипеда, в основании которого находится квадрат.

Пусть a-ширина, b-высота, c-длина, тогда

V=abc=334,4; a=c

V=a²b=334,4. Отсюдавыражаемb:

b=334,4/a²

Площадь полной поверхности прямоугольного параллелепипеда можно найти по формуле S=2а²+4аb.

Подставляем переменную b, выраженную через объём в уравнение:

S=2а²+4а*(334,4/а²)

Далее находим производную от площади, приравняем ее к нулю и найдем а:

а ³= 334,4

а = 6,942.

Проверяем знаки производной и с помощью прямой, убеждаемся что, а = 6,942 является наименьшим числом

 

 

 

и вычисляем b:

b =6,942

Подставим данные значения в формулу площади и получим

S= 289,148 см².

 

Мы получили до 26,8 см ² (316 – 289,148 ≈ 26,8) экономии материала с 1 коробки, но при условии, что основание коробки квадратное .

 

Анализ  полученных результатов

 

 

Из полученной таблицы можно сделать вывод: самая большая экономия наблюдается при изменении  упаковки «МК» - до 50,14 см²с одной коробки.

Чтобы представить объем экономии, рассмотрим пример.

 На 20000 таких коробок затраты уменьшаться около 1000000 см², это соответствует 100 м² картона. 100 м² картона весит  в среднем 20000г или 0,020 т. Так как на 1т уходит в среднем  10 деревьев,  то в нашем случае можно сохранить почти пол дерева.

 

Итак, мы получили экономичную упаковку для чая кубической формы с ребром = 6,887 см и новую упаковку «Липтон» с измененными размерами - 10,3×7,04×4,5 (в см).

Оптимальные размеры экономичной упаковки:

 

Таким образом, наша гипотеза подтвердилась: можно сохранить огромные запасы лесных ресурсов,  если вычислить  оптимальные размеры для изготовления упаковочных коробок.

 

V.               Заключение

Цель работы  достигнута:  используя найденные измерения прямоугольного параллелепипеда можно сократить расход картонного материала. Таким образом, математика вносит большой вклад в решении экологических проблем.

Данное исследование планируется продолжить и полученные размеры предложить производителям коробок. Необходимо еще учесть размеры припусков на швы и стандартные размеры габаритных коробок для перевозки. Маленькие коробочки перевозят в больших картонных коробках, которые имеют определённые стандарты. Обычно только транспортная тара может иметь стандартные размеры коробок – это 600х400х400 и 500х500х500 мм. Что касается потребительской упаковки, то тут стандартные размеры коробок предугадать очень сложно, так как такая упаковка подбирается в зависимости от размеров упаковываемого товара и его веса, а также от количества товара.

Эту работу можно использовать при изучении таких вопросов как прямоугольный параллелепипед по геометрии, производная функции по алгебре и началам анализа в 11 классе, а так же в подготовке к ЕГЭ.

 

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

 

1.                 Алгебра и начала математического анализа. Учебник (профильный уровень) для 10 кл.  Мордкович и . и др., 9-е издание, стереотипное. Издание мнемозина.: М, 2012.

2.                 А так ли хорошо знаком вам объем? // Квант. — 1993. — №1. — С. 40-41.

3.                 Образовательный портал для подготовки к экзаменам «Решу ЕГЭ» http://reshuege.ru/

4.                  Степановских А. С., Охрана окружающей среды, Москва: «Юнити», - 2000, - с.560, с. 186 – 192.

5.                  https://ru.wikipedia.org/wiki

6.                  Алгебра и начала математического анализа. Учебник для 10-11 кл.  Колмогоров А.Н. и др., 17-е изд. - М.: Просвещение, 2008.

7.                  http://www.lesprominform.ru/jarchive/articles/itemshow/2237

8.                  http://window.edu.ru/resource/694/21694

9.                  http://kartonpak.ru/products/347/

10.              http://www.ecosystema.ru/07referats/isp_les.htm

 

11.              Скачано с www.znanio.ru