Исследовательская работа "Знак "пи" "

Муниципальное образовательное учреждение

«Средняя общеобразовательная школа №22»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 «Магическое число π»

 

 

 

 

 

 

 

 

 

 

 

 

 

Выполнила: ученица 9А класса

Каткова Ирина

Учитель математики

Михайлова Л.Б.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г.Иркутск 2011

План работы:

 

1.     Введение

2.     Краткая «биография» числа π

3.     Преданья старины глубокой

4.     Квадратура круга

5.     Дальнейшее постижение числа π

6.     Число е

7.     Эра компьютеров

8.     Красота числа в формулах

9.     Число π и наука о природе

10. Различные способы вычисления числа π

11. Такое разное π

12.  π – клуб или клуб фанатиков числа π

13. Заключение

 

1.     ВВЕДЕНИЕ

 

«Пи-пи-пи-и-и, - пела скрипка, и Ёжик

прикрыл глаза – так ему было хорошо

                                                                            и печально»               

Сергей Козлов, «Весенняя сказка»

 

Гордый Рим трубил победу
       Над твердыней Сиракуз;
  Но трудами Архимеда
        Много больше я горжусь.
         Надо нынче нам заняться,
     Оказать старинке честь,
       Чтобы нам не ошибаться,
                Чтоб окружность верно счесть,
       Надо только постараться
      И запомнить все как есть
    Три — четырнадцать —
пятнадцать — девяносто два и шесть!

С.Бобров

 

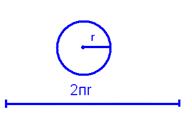Каждый человек компетентен в той области, которую он любит, в которой работает. Однако математика пронизывает все науки без исключения, и каждый из нас должен быть в ней более или менее компетентен. В математике есть удивительное и загадочное число. Это число p.  В последнее время число π стало привлекать людей, далеко не связанных с математикой. Среди бесконечного разнообразия чисел число π пользуется особой славой. О нём пишут  стихи, о нём сочиняют афоризмы, его изображают на полотнах и сегодня во всемирной паутине – компьютерной сети Internet ему посвящают сайты. В школьном курсе математики с числом p мы впервые встречаемся в 6 классе в теме: «Длина окружности и площадь круга». Потом, только в 9 классе мы опять встречаемся с числом p. Особое значение число p имеет в курсе «Алгебры и начал анализа» в 10 классе для измерения угла в радианах, при изучении темы «Тригонометрические функции».

Есть даже математический ребус на тему числа p: разгадав ребус, вы узнаете имя древнегрече­ского философа и математика, которому приписывают открытие важнейших теорем геометрии.

 

На этом школьная жизнь числа p не заканчивается. В старших классах мы встречаемся с этим удивительным числом в курсе физики в таких темах как:

 

 

 

 

1.      Движение тела по окружности:

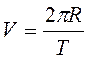  - линейная скорость;

- угловая скорость, n – частота вращения.

2.      Механическое напряжение:

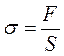 - S – площадь сечения (круга),

3.      Период колебания математического маятника:

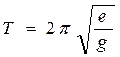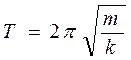 ,  - период колебания груза на пружине

4.      Закон Кулона:

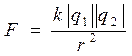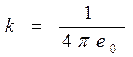 ,  - коэффициент пропорциональности

5.      Формула Томсона

 - период колебаний в колеблющемся контуре.

 

Но любая попытка разобраться со свойствами этого числа выводит нас за школьный курс математики. Вот и я решила побольше узнать о тайнах этого удивительного числа. Я была удивлена, узнав, какие страстные споры, бурные чувства вызывало число π у тех, кто им занимался. Этому числу удавалось в течение тысячелетий держать в плену мысли и чувства не только ученых, но и философов, и художников. История числа π лишний раз убеждает, что мысли тех, кто стремится к решению одной и той же задачи, не остаются изолированными во времени и в пространстве: они «ищут» друг друга и соединяются в единое целое, подобно звукам мелодии, связанным между собой законами гармонии. Когда решение математической задачи получено, его структура часто радует красотой и действует на ум и душу подобно звукам симфонии.

Число π можно сравнивать с кустом великолепных роз: слегка колышущемся на ветру, с прозрачными капельками от только что прошедшего дождя на хрупких стебельках и чудесных цветках, - он находится рядом, его хорошо видно, но приблизиться к нему вплотную , чтобы в полной мере ощутить и осязать все прелести аромата и мягкого шелеста его, невозможно, поскольку располагается он на другом краю пропасти.

Цель моей работы – это как бы краткий визит в мастерскую великого скульптора, называемого математикой через исследование природы числа «ПИ» и выявление его роли в окружающем нас мире.

Поставленная цель предполагает решение следующих задач:

1. Рассмотреть:

-        ситуации возникновения числа p.

-        трансцендентность числа p.

-        некоторые способы вычисления числа p.

-        проблему  квадратуры круга.

2. Провести собственный опыт исследования по вычислению числа p.
3. Раскрыть загадочность числа p.

 

 

2. КРАТКАЯ БИОГРАФИЯ ЧИСЛА π

 

                                                                - Вот и я говорю, - сказал Шалтай-Болтай.

- Все на одно лицо: два глаза,…в середине нос, а под ним – рот.

У всех одно и то же!

Льюис Кэрролл.

«Алиса в Зазеркалье»

 

Хотя число π является лишь одним из бесконечного множества действительных чисел, оно обратило на себя внимание людей еще в те времена, когда они не умели письменно излагать ни своих знаний, ни своих переживаний, ни своих воспоминаний. . Выражая величину отношения между длиной окружности и длиной ее диаметра -  -  оно появлялось во всех расчетах, связанных с площадью круга или длиной окружности. Из этого отношения  следует замечательный вывод: для любой окружности её длина С пропорциональна диаметру d c одним и тем же, не зависящим от окружности,  коэффициентом пропорциональности :

 

 

 

 

3. ПРЕДАНЬЯ СТАРИНЫ ГЛУБОКОЙ

 

- Ур халдеев, - сказал Профессор.

- Большие были умники, любили все круглое и

Знали число π. Оно у них равнялось трём.

Не очень точно, зато легко выучить.

Н.Герн.

«Новые приключения мистера Томпкинса»

 

Поскольку все окружности такие замечательные, что длину каждой из них можно найти, умножив её диаметр на одно и то же число, то чему равно это универсальное число – единый для всех окружностей коэффициент пропорциональности?

Представления о числе π претерпели удивительную эволюцию – от смутных представлений древних, экспериментально – буквально ощупью открывавших количественные закономерности окружающего мира до чрезвычайно глубоких математических теорий современности.

С тех пор как первые натуральные числа 1, 2, 3, … стали неразлучными спутниками человеческой мысли, помогая оценивать количества предметов либо их длины, площади или объемы, люди познакомились и с числом π. Тогда оно еще не обозначалось одной из букв греческого алфавита и его роль играло число 3. Но уже в глубокой древности математики довольно быстро и не без удивления обнаружили, что число 3 не совсем точно выражает то, что теперь известно как число π. К такому выводу они могли прийти только после того, как к ряду натуральных чисел добавились дробные числа.

 

 

Следующая задача содержится в одном из клинописных текстов, содержащихся в Британском музее: «60 длина окружности. 2, на сколько я спустился. Что есть хорда?» Речь в этой задаче идёт о вычислении длины хорды АВ, стрелка которой СD равна 2, причём длина окружности равна 60 (рис.1).

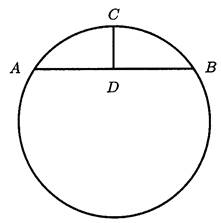
рис.1

 

В переводе на современный язык эта задача может быть сформулирована так: «Отбрось от диаметра его девятую часть и построй квадрат со стороной, равной остальной части, будет он эквивалентен кругу». Из этого следует, что у Ахмеса π  3,1605. Так началась письменная история π.

В Вавилоне в V в. До н.э. пользовались числом 3  3,1215, а в Древней Греции числом ()  3,1462643. В индийских «сутрах» VI – V в. До н.э. имеются правила, из которых вытекает, что π = 3,008. Наиболее древняя формулировка нахождения приблизительного значения отношения длины окружности к диаметру содержится в стихах индийского математика Аршабхата (V – VI в.):

 

Прибавь четыре к сотне и умножь на восемь,

Потом еще шестьдесят две тысячи прибавь,

Как поделить результат на двадцать тысяч,

Тогда откроется тебе значение

Длины окружности к двум радиусам отношенья,

т.е.  =

 

В дошедших до нас с незапамятных времен математических текстах встречаются приближения числа π различной точности. Все их можно охарактеризовать одной фразой: значение для π есть, но из каких соображений оно было получено – неизвестно. Скорее всего, древние тщательно анализировали и сопоставляли результаты измерений окружающих их предметов. Ниже приводятся некоторые сведения о найденных древними математиками приближениях для числа π. Происхождение их неизвестно.

Индусы в V – VI пользовались числом 3,1611, а китайцы – числом   3,1415927; это значение записывалось в виде именованного числа:

3 чжана 1 чи 4 цуня 1 фень 5 ме 9 хао 2 мяо 7 хо.

Долгое время все пользовались значением числа, равным . Но это равенство ошибочное. Предлагаю вам решить следующую головоломку: переложите одну спичку так, чтобы равенство стало верным (рис.2):

 

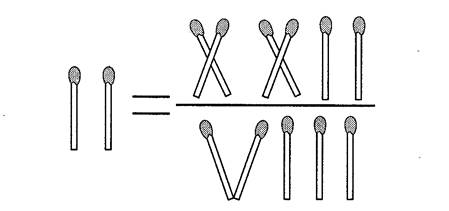
рис.2

 

Оказывается, для решения надо одну из вертикальных спичек в знаменателе следует убрать и сделать из неё «крышечку» в левой части равенства. Таким образом образуется стилизованное изображение буквы π.

В чем причина ошибочного отождествления числа π с дробью ? По всей видимости, причину нужно искать в кривом зеркале популярности великого ученого. На Амом деле Архимеду удалось не только найти это довольно хорошее приближение для числа π, но и, - что гораздо важнее, определить точность этого приближения, то есть указать узкий промежуток числовой оси, которому принадлежит отношение длины окружности к ее диаметру. Архимед получил:  , т.е. π  3,1418.

 

 

В XV веке иранский математик Аль-Каши нашел значение π с 16-ю верными знаками, рассмотрев вписанный и описанный многоугольники с 80.035.168 сторонами.

Андриан Ван Ромен (Бельгия) в XVI в. С помощью 2³⁰-угольников получил 17 верных десятичных знаков.

Голландский вычислитель – Лудольф Ван-Цейлен (1540 – 1610), вычисляя π, дошел до многоугольников с 60 20²⁹ сторонами, и получил 35 верных знаков для π. Ученый обнаружил большое терпение и выдержку, несколько лет затратив на определение числа π. В его часть современники назвали π – «Лудольфово число». Согласно завещанию на его надгробном камне было высечено найденное им значение π.

В 1767 году Аанн Ламберт (немецкий математик) доказал традиционность числа π.

 

 

 

 

 

 

 

 

 

 

 

 

 

4.     КВАДРАТУРА КРУГА

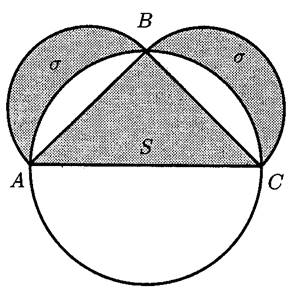Задача о квадратуре круга заключается в следующем: построить квадрат, площадь которого была бы равна площади данного круга. Задача о квадратуре круга – одна из трёх знаменитых задач древности. Она возникла на заре человеческой культуры и её история охватывает период около четырёх тысяч лет. Этой задачей раньше греков занимались вавилоняне и египтяне. Независимо от греков ею занимались китайцы и индийцы. Особенно большое распространение эта задача получила в древней Греции. Древнегреческие учёные стремились задачу о квадратуре круга решить при помощи циркуля и линейки. Показательна в этом отношении работа Гиппократа Хиосского, которому удалось криволинейную фигуру (гиппократовы луночки – рис.3) преобразовать в равновеликий ей многоугольник. Однако, преобразовать круг в равновеликий ему квадрат, Гиппократу так и не удалось, так как он в рассуждениях допустил ошибку.

Окончательный удар всем иллюзиям решить задачу о квадратуре круга при помощи циркуля и линейки был нанесён лишь во второй половине XIX в. Немецкому математику Фердинанду Линдеману в 1882 году удалось, наконец, вполне строго доказать, что задача о квадратуре круга неразрешима при помощи циркуля и линейки и все старания что-нибудь сделать в этом направлении указанными средствами являются совершенно напрасными и ненужными. Вот почему Фердинанда Линдемана называют «победителем числа p», а ещё лучше – «победителем задачи о квадратуре круга». Если бы могли представить p в виде рациональной дроби или корня линейного или квадратного уравнения, то с помощью циркуля и линейки нам нетрудно было бы построить отрезок прямой, длина которого была бы в точности равна половине длины окружности. Отсюда уже совсем просто было бы получить квадратуру круга: для этого достаточно построить прямоугольник, у которого одна сторона равна радиусу окружности, а другая – половине её длины. Площадь такого прямоугольника равна площади круга, а превратить его в равновеликий квадрат легко. Наоборот, если бы задача о квадратуре круга была разрешима, то это бы означало, что мы можем построить отрезок прямой, длина которого была бы в точности равна p. Однако существуют совершенно строгие доказательства трансцендентности числа p и невозможности построения с помощью циркуля и линейки отрезка, длина которого выражается трансцендентным числом.

Предлагались сотни способов приближенного построения p; одно из наиболее точных построений основано на уже упоминавшемся нами приближенном представлении числа p в виде рациональной дроби, найденном китайским астрономом. Проведём в четверти единичного круга несколько линий (рис. 4) так, чтобы отрезок bc был равен 7/8 радиуса, dg- 1/2, отрезок de был параллелен отрезку ас, a df— параллелен отрезку be.

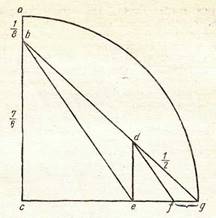
рис. 4

Расстояние fg равно , или 0,1415929… Поскольку , отложим отрезок втрое длиннее радиуса, продолжим его на расстояние fg и получим новый отрезок, длина которого отличается от  p меньше чем на одну миллионную.

Тысячи людей, бившихся над решением задачи о квадратуре круга, были уверены, что им удалось построить отрезок, длина которого в точности равна p, но никто из них не смог превзойти английского философа Томаса Гоббса, в котором высокий интеллект сочетался с глубочайшим невежеством. Во времена Гоббса даже образованного англичанина не обучали математике, поэтому Гоббс до сорока лет не заглядывал в «Начала» Евклида. Впервые в жизни прочитав формулировку теоремы Пифагора, он воскликнул: «Боже, но это невозможно!» Однако затем шаг за шагом он проследил всё доказательство и убедился в его правильности. С тех пор и до конца своей долгой жизни Гоббс с пылом влюбленного все свои помыслы безраздельно отдавал геометрии. «Геометрия чем-то напоминает вино», – писал он позднее. Рассказывают, что, когда у него под рукой не оказывалось более подходящей поверхности, Гоббс имел обыкновение чертить геометрические фигуры у себя на ноге или на простынях.

Если бы Гоббс так и остался любителем, то его последующие годы протекали бы более спокойно, однако чудовищное самомнение привело к тому, что он возомнил себя способным на великие математические открытия. В 1665 году, в возрасте 67 лет, он выпустил в свет на латинском языке книгу под названием «De corpore» («О телах»), в которой, помимо прочего, излагался остроумный метод решения задачи о квадратуре круга. Его метод и в самом деле позволял найти превосходное приближение числа p, но Гоббс считал свой метод точным. Джон Валлис, знаменитый английский математик и специалист по криптографии, изложил ошибки Гоббса в памфлете («Памфлет» - злободневное острое, обычно небольшое сочинение обличительного, политического характера. Так началась самая продолжительная, нелепейшая и бесполезнейшая словесная перепалка, в которой когда–либо участвовали два блестящих ума. Спор длился почти четверть века, обе стороны перемежали в своих публичных выступлениях едкий сарказм грубой бранью.

С небольшими перерывами борьба продолжалась до самой смерти Гоббса, последовавшей на 91-м году жизни. «Мистер Гоббс всегда был далек от мысли бросать кому – нибудь вызов, – писал Гоббс, в одной из своих филиппик (Филиппик – гневная обличительная речь, выступление против кого-л., чего-л. Против Валлиса (и действительно, в отношениях с другими людьми Гоббс был крайне робок), – но, бросив ему вызов, вы убедитесь, что перо его не уступит в остроте вашему. Всё сказанное вами состоит наполовину из брани. Оно ничем не отличается от того зловония, которое испускает старая кляча, если, обкормив её овсом, мы слишком туго затянем подпругу. Я кончил. Я уделил вам достаточно внимания и не намерен возвращаться к этому неприятному для меня занятию вновь…». Мы не будем подробно обсуждать здесь то, что Валлис назвал удивительной «неспособностью» Гоббса «научиться тому, чего он не знает». Достаточно сказать, что Гоббс опубликовал около десятка различных способов решения задачи о квадратуре круга. Одну из главных причин всех затруднений Гоббса понять нетрудно. Он никак не мог привыкнуть к мысли о том, что точки, линии и поверхности можно рассматривать абстрактно как геометрические объекты, размерность которых меньше трех. «По – видимому, он так и ушёл в могилу, – пишет в книге «Ссоры авторов» Исаак Дизраэли, – с твердым убеждением, что поверхности обладают и глубиной, и толщиной, несмотря на все возражения геометров, выслушанные им при жизни». Гоббс представляет собой классический пример человека выдающихся способностей, вступившего в область науки, для которой он плохо подготовлен, и растратившего всю энергию на решение пустых псевдонаучных вопросов.

Итак, задача о квадратуре круга оказалась сложной. Только в 1882 г. Фердинанд Линдеман доказал, что число π трансцендентно, т.е. не является корнем никакого многочлена с целыми коэффициентами. Значит, оно и не квадратично-иррационально, поскольку в противном случае было бы корнем какого-либо многочлена. Так Линдеман наконец поставил точку в проблеме разрешимости посредством циркуля и линейки последней из трех классических задач древности. В память об открытии трансцендентности числа π в зале перед математической аудиторией Мюнхенского университета был установлен бюст Линдемана. На постаменте под его именем изображен круг, пересеченный квадратом равной площади, внутри которого начертана буква π.

 

 

 

 

 

 

5.     ДАЛЬНЕЙШЕЕ ПОСТИЖЕНИЕ ЧИСЛА π

 

Учёным задали вопрос: «Чему равно π?»

Инженер отвечает: «Это приблизительно ».

Физик говорит: «Это 3,14159».

                                                          Математик (после небольшого

              раздумья) : «Это равно π».

 

Одно из простейших выражений для π открыл (середина XVII в.) Джон Валлис (английский математик):

π = 2()

 

А несколько десятилетий спустя великий немецкий философ Готфрид-Вильгельм Лейбниц открыл другую изящную формулу:

π = 4()

 

Самым неутомимым вычислителем π был английский математик Уильям Шенкс (конец XIX в.). Более 20 лет жизни он посвятил вычислению 707 знаков числа π. К сожалению, он ошибся в 520-ом знаке и все последующие цифры неверны. (Ошибку обнаружили лишь в 1945 году). Самое странное в найденных Шенксом 707 знаках p заключается в том, что эти знаки «свысока» смотрят на цифру 7: если каждая из остальных цифр, как и должно быть, встречается среди первых 700 знаков около 70 раз, то семерка появляется лишь 51 раз.

В 1699 году Авраамом Шарпом (1651 – 1742) было установлено рекордное количество для вычисления числа, состоящее из 71 точного десятичного знака числа π. Ученый воспользовался разложением

.

А вот разложение вида  позволило Джону Мэчину вычислить 100 десятичных знаков числа π. Его результат был опубликован в 1706 году У.Джонсоном в работе «Обозрение достижений математики», где впервые зарегистрировано использование буквы π для обозначения отношения длины окружности к диаметру.

Успехи Шенкса и Мэчина окрылили других вычислителей, и они с азартом присоединились к удивительному соревнованию, начатому математиками.

Де Ланьи (1660 – 1734), используя метод Шарпа, в 1719 году вычисляет 127 точных десятичных знаков числа  π . Вскоре Леонард Эйлер другим способом проверил результат Ланьи и обнаружил ошибку в 113 знаке.

В 1794 году Вега указал значение π с точностью до 140 десятичных знаков, из которых точными оказались 136.

В 1841 году Уильям Резерфорд сообщает 208 десятичных знаков. Его результат перепроверил талантливый гамбургский вычислитель Захария Дазе. Дазе показал, что Резерфорд ошибся, начиная со 153 знака.

В 1844 году Дазе довел точность до 205 знаков, из которых 200 были вычислены верно.

В 1847 году Томас Клаузен продвинулся до 250 знаков, из которых 248 были точны.

В 1853 году Резерфорд увеличил совё достижение до 440 десятичных знаков. Рекорд этого года устанавливает Уильям Шенкс – 530 знаков (из них 527 верных). В последующем Шенкс упорно работает над вычислениями новых знаков, доведя их количество до 707, но ошибка в 528 знаке свела на нет все его дальнейшие усилия.

  

6. ЧИСЛО е

 

Дальнейшее постижение числа π стало возможным благодаря его неожиданному «союзнику» - числу е, которое в 1736 году ввел и предложил так обозначать Леонард Эйлер. Число . Оно замечательно во многих отношениях. Для него существуют красивые разложения:  

или такое разложение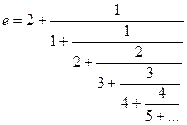

Эйлеру принадлежит изумительная по красоте формула, собирающая в один «букет» примечательные математические константы: . Это тождество было опубликовано Эйлером в 1748 году. Ныне оно высечено над дверью математического отделения парижского Дворца Открытий.

Иррациональные числа π и е оказываются связанными между собой довольно неожиданными зависимостями: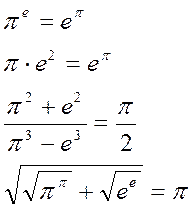

 

 

7. ЭРА КОМПЬЮТЕРОВ

    

Двадцатый век вошел в историю человеческой цивилизации не только своими разрушительными войнами. Он ознаменовался компьютерной революцией. Уже первые проверки на появившихся в 1945 году ЭВМ показали, что Уильям Шенкс в своих расчётах ошибся, начиная с 528 знака, так что весь последующий «хвост» из 180 знаков оказался неверным. С появлением компьютеров темпы погони за точными десятичными знаками числа π резко ускорилось. В 1949 году электронно-вычислительная машина «ЭНИАК», проработав в течение 70 часов, вычислила более 2000 знаков числа p. Позднее с помощью другой вычислительной машины, проработавшей всего лишь 13 минут, были вычислены 3000 знаков p. В 1959 году одна вычислительная машина в Англии и другая во Франции вычислили 10000 десятичных знаков p. В 1961 году машина IBM - 7090 вычислила p с точностью до 100625 знаков. Программа была составлена Дэниэлом Шенксом (не имеющим никакого отношения к Уильяму Шенксу; это лишь одно из тех странных совпадений, которыми изобилует история числа p) и Джоном У. Ренчем младшим. Машинное время составило 8 час 1 мин; ещё 42 мин потребовалось для того, чтобы перевести результат из двоичной в десятичную форму. Вычисление нескольких тысяч знаков p в настоящее время стало популярным средством проверки новых вычислительных машин и обучения молодых программистов. «Загадочное и чудесное p – пишет в своей книге «Что мы знаем о больших числах» Филипп Дж. Девис, – стало чем–то вроде покашливания, которым вычислительные машины прочищают горло».  

В конце прошлого столетия посетители сайта www/cecm/sfu/ca/projects/pihex встречали объявление, приглашающее их принять участие в глобальном проекте «Pi – Hex». Любой житель Земли, подключив свой компьютер к сети Internet, мог стать участником коллективных вычислений отдельных цифр двоичной записи числа «пи». Координатором этого глобального проекта выступил студент университета Симона Фрезера (США) Колин Персивал. В проекте приняло участие около 2000 добровольцев.

Предлагаю краткую хронологию вычислений:

1949 год- 2037 десятичных знаков (Джон фон Нейман, ENIAC),
1958 год- 10000 десятичных знаков (Ф.Женюи, IBM-704),
1961 год- 100000 десятичных знаков (Д.Шенкс, IBM-7090),
1973 год- 10000000 десятичных знаков (Ж.Гийу, М.Буйе, CDC-7600),
1986 год- 29360000 десятичных знаков (Д.Бейли, Cray-2),
1987 год- 134217000 десятичных знаков (Т.Канада, NEC SX2),
1989 год- 1011196691 десятичных знаков (Д.Чудновски и Г.Чудновски, Cray-2+IBM-3040) Они же добились в 1991 году 2260000000 знаков, а в 1994 году - 4044000000 знаков.
Дальнейшие рекорды принадлежат японцу Тамуре Канада: в 1995 году 4294967286 знаков, в 1997 - 51539600000, 2000 -  206.158.430.000 знаков. Суперкомпьютер (проект HINTS - High-performance Numerical Tools & Software для сверхмощных научных и инженерных вычислений.  На сегодняшний день известны первые 1 242 100 000 000 знака.

Остановится ли когда-нибудь удивительная погоня за исчезающими в бесконечности знаками числа? – По-видимому, этот вопрос можно переформулировать так: прекратит ли когда-нибудь свое существование человеческая цивилизация?

А теперь предлагаю всем прикоснуться к вершине достижения человеческого разума, впитавшего знания, энтузиазм и судьбы тысяч математиков-вычислителей за последние 4000 лет. Рассмотрите внимательно, его первые тысячи знаков, проникнитесь поэзией этих цифр, ведь за ними стоят история нашей цивилизации, жизни сотен лучших умов человечества и тайна устройства мироздания. Есть гипотезы, предполагающие, что в числе Пи скрыта любая информация, которая когда либо была или будет доступна людям.

3.
1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 8214808651 3282306647 0938446095 5058223172 5359408128 4811174502 8410270193 8521105559 6446229489 5493038196 4428810975 6659334461 2847564823 3786783165 2712019091 4564856692 3460348610 4543266482 1339360726 0249141273 7245870066 0631558817 4881520920 9628292540 9171536436 7892590360 0113305305 4882046652 1384146951 9415116094 3305727036 5759591953 0921861173 8193261179 3105118548 0744623799 6274956735 1885752724 8912279381 8301194912 9833673362 4406566430 8602139494 6395224737 1907021798 6094370277 0539217176 2931767523 8467481846 7669405132 0005681271 4526356082 7785771342 7577896091 7363717872 1468440901 2249534301 4654958537 1050792279 6892589235 4201995611 2129021960 8640344181 5981362977 4771309960 5187072113 4999999837 2978049951 0597317328 1609631859 5024459455 3469083026 4252230825 3344685035 2619311881 7101000313 7838752886 5875332083 8142061717 7669147303 5982534904 2875546873 1159562863 8823537875 9375195778 1857780532 1712268066 1300192787 6611195909 2164201989 3809525720 1065485863 2788659361 5338182796 8230301952 0353018529 6899577362 2599413891 2497217752 8347913151 5574857242 4541506959 5082953311 6861727855 8890750983 8175463746 4939319255 0604009277 0167113900 9848824012 8583616035 6370766010 4710181942 9555961989 4676783744 9448255379 7747268471 0404753464 6208046684 2590694912 9331367702 8989152104 7521620569 6602405803 8150193511 2533824300 3558764024 7496473263 9141992726 0426992279 6782354781 6360093417 2164121992 4586315030 2861829745 5570674983 8505494588 5869269956 9092721079 7509302955 3211653449 8720275596 0236480665 4991198818 3479775356 6369807426 5425278625 5181841757 4672890977 7727938000 8164706001 6145249192 1300192787 6611195909 2164201989 1732172147 7235014144 1973568548 1613611573 5255213347 5741849468 4385233239 0739414333 4547762416 8625189835 6948556209 9219222184 2725502542 5688767179 0494601653 4668049886 2723279178 6085784383 8279679766 8145410095 3883786360 9506800642 2512520511 7392984896 0841284886 2694560424 1965285022 2106611863 0674427862 2039194945 0471237137 8696095636 4371917287 4677646575 7396241389 0865832645 9958133904 7802759009 9465764078 9512694683 9835259570 9825822620 5224894077 2671947826 8482601476 9909026401 3639443745 5305068203 4962524517 4939965143 1429809190 6592509372 2169646151 5709858387 4105978859 5977297549 8930161753 9284681382 6868386894 2774155991 8559252459 5395943104 9972524680 8459872736 4469584865 3836736222 6260991246 0805124388 4390451244 1365497627 8079771569 1435997700 1296160894 4169486855 5848406353 4220722258 2848864815 8456028506 0168427394 5226746767 8895252138 5225499546 6672782398 6456596116 3548862305 7745649803 5593634568 1743241125 1507606947 9451096596 0940252288 7971089314 5669136867 2287489405 6010150330 8617928680 9208747609 1782493858 9009714909 6759852613 6554978189 3129784821 6829989487 2265880485 7564014270 4775551323 7964145152 3746234364 5428584447 9526586782 1051141354 7357395231 1342716610 2135969536 2314429524 8493718711 0145765403 5902799344 0374200731 0578539062 1983874478 0847848968 3321445713 8687519435 0643021845 3191048481 0053706146 8067491927 8191197939 9520614196 6342875444 0643745123 7181921799 9839101591 9561814675 1426912397 4894090718 6494231961 5679452080 9514655022 5231603881 9301420937 6213785595 6638937787 0830390697 9207734672 2182562599 6615014215 0306803844 7734549202 6054146659 2520149744 2850732518 6660021324 3408819071 0486331734 6496514539 0579626856 1005508106 6587969981 6357473638 4052571459 1028970641 4011097120 6280439039 7595156771 5770042033 7869936007 2305587631 7635942187 3125147120 5329281918 2618612586 7321579198 4148488291 6447060957 5270695722 0917567116 7229109816 9091528017 3506712748 5832228718 3520935396 5725121083 5791513698 8209144421 0067510334 6711031412 6711136990 8658516398 3150197016 5151168517 1437657618 3515565088 4909989859 9823873455 2833163550 7647918535 8932261854 8963213293 3089857064 2046752590 7091548141 6549859461 6371802709 8199430992 4488957571 2828905923 2332609729 9712084433 5732654893 8239119325 9746366730 5836041428 1388303203 8249037589 8524374417 0291327656 1809377344 4030707469 2112019130 2033038019 7621101100 4492932151 6084244485 9637669838 9522868478 3123552658 2131449576 8572624334 4189303968 6426243410 7732269780 2807318915 4411010446 8232527162 0105265227 2111660396 6655730925 4711055785 3763466820 6531098965 2691862056 4769312570 5863566201 8558100729 3606598764 8611791045 3348850346 1136576867 5324944166 8039626579 7877185560 8455296541 2665408530 6143444318 5867697514 5661406800 7002378776 5913440171 2749470420 5622305389 9456131407 1127000407 8547332699 3908145466 4645880797 2708266830 6343285878 5698305235 8089330657 5740679545 7163775254 2021149557 6158140025 0126228594 1302164715 5097925923 0990796547 3761255176 5675135751 7829666454 7791745011 2996148903 0463994713 2962107340 4375189573 5961458901 9389713111 7904297828 5647503203 1986915140 2870808599 0480109412 1472213179 4764777262 2414254854 5403321571 8530614228 8137585043 0633217518 2979866223 7172159160 7716692547 4873898665 4949450114 6540628433 6639379003 9769265672 1463853067 3609657120 9180763832 7166416274 8888007869 2560290228 4721040317 2118608204 1900042296 6171196377 9213375751 1495950156 6049631862 9472654736 4252308177 0367515906 7350235072 8354056704 0386743513 6222247715 8915049530 9844489333 0963408780 7693259939 7805419341 4473774418 4263129860 8099888687 4132604721 5695162396 5864573021 6315981931 9516735381 2974167729 4786724229 2465436680 0980676928 2382806899 6400482435 4037014163 1496589794 0924323789 6907069779 4223625082 2168895738 3798623001 5937764716 5122893578 6015881617 5578297352 3344604281 5126272037 3431465319 7777416031 9906655418 7639792933 4419521541 3418994854 4473456738 3162499341 9131814809 2777710386 3877343177 2075456545 3220777092 1201905166 0962804909 2636019759 8828161332 3166636528 6193266863 3606273567 6303544776 2803504507 7723554710 5859548702 7908143562 4014517180 6246436267 9456127531 8134078330 3362542327 8394497538 2437205835 3114771199 2606381334 6776879695 9703098339 1307710987 0408591337 4641442822 7726346594 7047458784 7787201927 7152807317 6790770715 7213444730 6057007334 9243693113 8350493163 1284042512 1925651798 0694113528 0131470130 4781643788 5185290928 5452011658 3934196562 1349143415 9562586586 5570552690 4965209858 0338507224 2648293972 8584783163 0577775606 8887644624 8246857926 0395352773 4803048029 0058760758 2510474709 1643961362 6760449256 2742042083 2085661190 6254543372 1315359584 5068772460 2901618766 7952406163 4252257719 5429162991 9306455377 9914037340 4328752628 8896399587 9475729174 6426357455 2540790914 5135711136 9410911939 3251910760 2082520261 8798531887 7058429725 9167781314 9699009019 2116971737 2784768472 6860849003 3770242429 1651300500 5168323364 3503895170 2989392233 4517220138 1280696501 1784408745 1960121228 5993716231 3017114448 4640903890 6449544400 6198690754 8516026327 5052983491 8740786680 8818338510 2283345085 0486082503 9302133219 7155184306 3545500766 8282949304 1377655279 3975175461 3953984683 3936383047 4611996653 8581538420 5685338621 8672523340 2830871123 2827892125 0771262946 3229563989 8989358211 6745627010 2183564622 0134967151 8819097303 8119800497 3407239610 3685406643 1939509790 1906996395 5245300545 0580685501 9567302292 1913933918 5680344903 9820595510 0226353536 1920419947 4553859381 0234395544 9597783779 0237421617 2711172364 3435439478 2218185286 2408514006 6604433258 8856986705 4315470696 5747458550 3323233421 0730154594 0516553790 6866273337 9958511562 5784322988 2737231989 8757141595 7811196358 3300594087 3068121602 8764962867 4460477464 9159950549 7374256269 0104903778 1986835938 1465741268 0492564879 8556145372 3478673303 9046883834 3634655379 4986419270 5638729317 4872332083 7601123029 9113679386 2708943879 9362016295 1541337142 4892830722 0126901475 4668476535 7616477379 4675200490 7571555278 1965362132 3926406160 1363581559 0742202020 3187277605 2772190055 6148425551 8792530343 5139844253 2234157623 3610642506 3904975008 6562710953 5919465897 5141310348 2276930624 7435363256 9160781547 8181152843 6679570611 0861533150 4452127473 9245449454 2368288606 1340841486 3776700961 2071512491 4043027253 8607648236 3414334623 5189757664 5216413767 9690314950 1910857598 4423919862 9164219399 4907236234 6468441173 9403265918 4044378051 3338945257 4239950829 6591228508 5558215725 0310712570 1266830240 2929525220 1187267675 6220415420 5161841634 8475651699 9811614101 0029960783 8690929160 3028840026 9104140792 8862150784 2451670908 7000699282 1206604183 7180653556 7252532567 5328612910 4248776182 5829765157 9598470356 2226293486 0034158722 9805349896 5022629174 8788202734 2092222453 3985626476 6914905562 8425039127 5771028402 7998066365 8254889264 8802545661 0172967026 6407655904 2909945681 5065265305 3718294127 0336931378 5178609040 7086671149 6558343434 7693385781 7113864558 7367812301 4587687126 6034891390 9562009939 3610310291 6161528813 8437909904 2317473363 9480457593 1493140529 7634757481 1935670911 0137751721 0080315590 2485309066 9203767192 2033229094 3346768514 2214477379 3937517034 4366199104 0337511173 5471918550 4644902636 5512816228 8244625759 1633303910 7225383742 1821408835 0865739177 1509682887 4782656995 9957449066 1758344137 5223970968 3408005355 9849175417 3818839994 4697486762 6551658276 5848358845 3142775687 9002909517 0283529716 3445621296 4043523117 6006651012 4120065975 5851276178 5838292041 9748442360 8007193045 7618932349 2292796501 9875187212 7267507981 2554709589 0455635792 1221033346 6974992356 3025494780 2490114195 2123828153 0911407907 3860251522 7429958180 7247162591 6685451333 1239480494 7079119153 2673430282 4418604142 6363954800 0448002670 4962482017 9289647669 7583183271 3142517029 6923488962 7668440323 2609275249 6035799646 9256504936 8183609003 2380929345 9588970695 3653494060 3402166544 3755890045 6328822505 4525564056 4482465151 8754711962 1844396582 5337543885 6909411303 1509526179 3780029741 2076651479 3942590298 9695946995 5657612186 5619673378 6236256125 2163208628 6922210327 4889218654 3648022967 8070576561 5144632046 9279068212 0738837781 4233562823 6089632080 6822246801 2248261177 1858963814 0918390367 3672220888 3215137556 0037279839 4004152970 0287830766 7094447456 0134556417 2543709069 7939612257 1429894671 5435784687 8861444581 2314593571 9849225284 7160504922 1242470141 2147805734 5510500801 9086996033 0276347870 8108175450 1193071412 2339086639 3833952942 5786905076 4310063835 1983438934 1596131854 3475464955 6978103829 3097164651 4384070070 7360411237 3599843452 2516105070 2705623526 6012764848 3084076118 3013052793 2054274628 6540360367 4532865105 7065874882 2569815793 6789766974 2205750596 8344086973 5020141020 6723585020 0724522563 2651341055 9240190274 2162484391 4035998953 5394590944 0704691209 1409387001 2645600162 3742880210 9276457931 0657922955 2498872758 46101264836999892256 9596881592 0560010165 5256375678

Эти цифры позаимствованы на http://www.joyofpi.com/pi.htm - одной из страничек, посвященных числу Пи. Там же вы найдете адресс The Joy of Pi миллиона знаков Пи. Но сначала лучше просмотрите 100.000 знаков.

 

В первых 200,000,000,000 десятичных знаках Пи цифры встречались с такой частотой:
'0' : 20000030841;
'1' : 19999914711;
'2' : 20000136978;
'3' : 20000069393
'4' : 19999921691;
'5' : 19999917053;
'6' : 19999881515;
'7' : 19999967594
'8' : 20000291044;
'9' : 19999869180.

8. КРАСОТА ЧИСЛА В ФОРМУЛАХ

 

   На вкус и цвет товарищей нет», - гласит поговорка. И все же, существуют объекты, относимые большинством из нас к категории прекрасных. Среди изящных человеческих творений – не только общепризнанные произведения искусства, к ним без всякого сомнения можно отнести и красивые математические формулы.

 

КОМПОЗИЦИИ АРИАБХАТЫ

 

Индийский математик и астроном 6 века является автором следующих замечательных композиций:

 

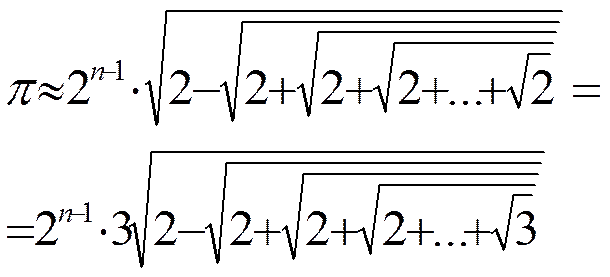
ФОРМУЛА ВАЛЛИСА

 

 

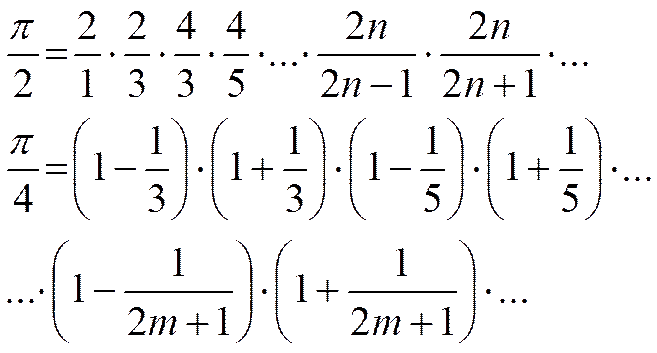
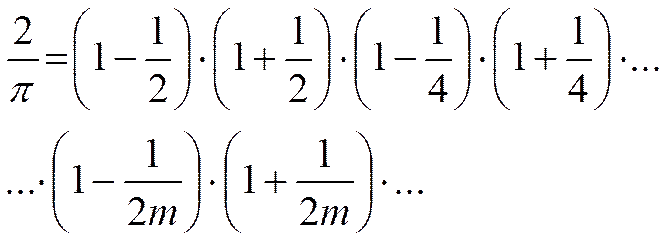
КОНСТРУКЦИЯ БРОУНКЕРА И ДРОБИ ЭЙЛЕРА

 

Любопытное разложение в цепную дробь нашел лорд Уильям Броункер (1620 – 1684) в 1665 году:

 

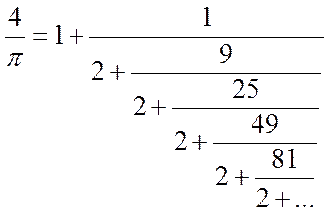
Доказательство этой формулы дал Леонард Эйлер в 1785 году, попутно указав другие цепные дроби, связанные с числом p:

 

 

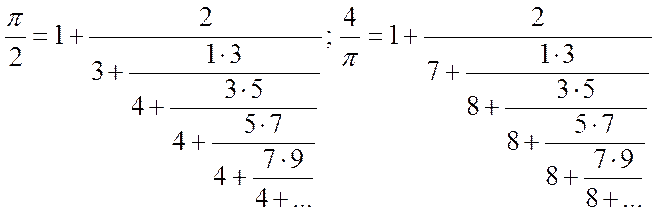
ФОРМУЛЫ ЭЙЛЕРА

 

 

 

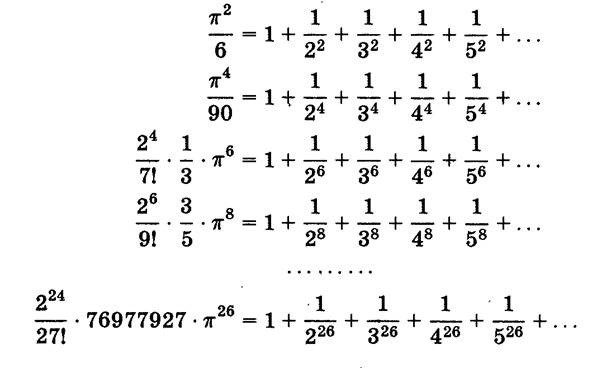
p И ЧИСЛА ФИБОНАЧЧИ

 

Леонардо Пизанский по прозвищу Фибоначчи (сын Боначчи) (1180 – 1240), скорее всего, не подозревал, что одна из задач, опубликованных в его книге «Liber Abacci» (1228), обессмертит его имя. Речь в этой задаче шла о размножающихся кроликах, количество которых образовывает замечательную последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,…Каждый новый член этой последовательности, начиная с третьего, равен сумме двух предыдущих. Последовательность чисел Фибоначчи удивительным образом возникает в самых неожиданных приложениях, и ей посвящена обширная литература. Последовательность чисел Фибоначчи с числом  p роднит формула Д.Х.Лемера:

 

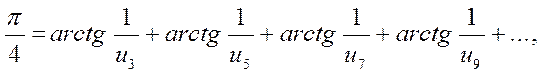
где u _n – числа Фибоначчи.

ФОРМУЛЫ ДЖЕРОМА К.Р.ЛИ

 

 

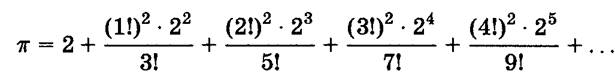
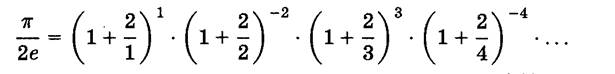
ФОРМУЛА Э.Х.КЛАРКА

 

 

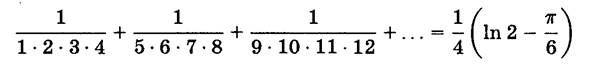
ФОРМУЛА Х.Ф.СЭНДХЕМА

 

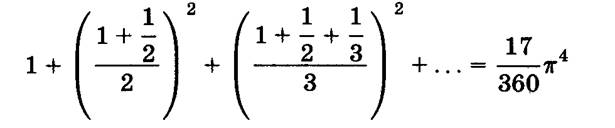
ФОРМУЛА М.БИЛЛЕРА

 

 

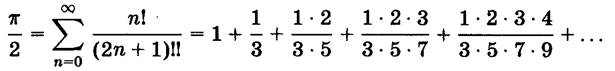
9. ЧИСЛО π И НАУКА О ПРИРОДЕ

 

Число π в физике не менее популярно, чем в математике. Оно возникает при оценке объемов и площадей цилиндрических тел: труб, цистерн, резервуаров; при расчете плотности потока излучения от точечного источника или цилиндрического проводника, при оценке квантовых состояний атома, при вычислении параметров гармонических колебаний и во многих-многих других случаях.

Ниже я приведу несколько задач, решение которых связано с числом π. Все задачи взяты из книги А.В.Жукова «Вездесущее число «пи».

ЗАДАЧА №1  «π – ТЕОРЕМА»

 

Так, свидетельствуя свои симпатии к числу π, физики назвали теорему теории размерностей. Речь в π – теореме идет о построении таких комбинаций размерных физических величин, которые сами, как и число π, являлись бы безразмерными. Всякое соотношение между n размерными величинами, для измерения которых использовано k основных единиц измерения, можно представить в виде соотношения между n ­ k безразмерными комбинациями этих величин.

 

 

ЗАДАЧА №2     «π И МОДЕЛЬ ПАДАЮЩЕГО БУТЕРБРОДА»

 

ЗАДАЧА №3  «ЗАКОН СОХРАНЕНИЯ π»

 

ЗАДАЧА №4 «π И ВНЕЗЕМНЫЕ ЦИВИЛИЗАЦИИ»

«Если я принимаю сигнал π,

мне уже не надо вспоминать,

чему равно это π»

Генри Каттнер

«Маскировка»

 

 

10. РАЗЛИЧНЫЕ СПОСОБЫ ВЫЧИСЛЕНИЯ ЧИСЛА π

Простейшее измерение

Начертим на плотном картоне окружность радиусом R, вырежем получившийся круг и обмотаем вокруг него тонкую нить. Измерив длину l одного полного оборота нити, разделим l на длину диаметра окружности. Получившееся частное будет приближенным значением числа π, т.е. π = . Данный довольно грубый способ дает в обычных условиях приближенное значение числа π с точностью до 1.

Измерение с помощью взвешивания

На месте картона начертим квадрат. Впишем в него круг. Вырежем квадрат. Определим масса картонного квадрата с помощью весов. Вырежем из квадрата круг. Взвесим и его. Зная массы квадрата (m_кв) и вписанного в него круга (m_кр), воспользуемся формулами

m = ρV₃ V = Sh,  где ρ и h - соответственно плотность и толщина картона, S – площадь фигуры.

Рассмотрим равенства: m_кв = ρ * π R² * h.

Отсюда , т.е. π =

Естественно, что в данном случае приближенное значение π зависит от точности взвешивания. Если взвешиваемые картонные фигуры будут довольно большими, то возможно даже на обычных весах получить такие значения масс, которые обеспечат приближение числа π с точностью до 0,1. Суммирование площадей прямоугольников, вписанных в полукруг.

Метод Монте-Карло

Это фактически метод статистических испытаний. Свое экзотическое название получил от города Монте-Карло в княжестве Монако, знаменитого своими игорными домами. Дело в том, что метод требует применения случайных чисел, а одним из простейших приборов, генерирующих случайные числа, может служить рулетка. Впрочем, можно получить случайные числа и при помощи… дождя.

Для опыта приготовим кусок картона, нарисуем на нем квадрат и впишем в квадрат четверть круга. Если такой чертеж некоторое время подержать под дождем, то на его поверхности останутся следы капель. Подсчитаем число следов внутри квадрата и внутри четверти круга. Очевидно, что их отношение будет приближенно равно отношению площадей этих фигур, так как попадание капель в различные места чертежа равновероятно. Пусть N_кр – число капель в кругу, N_кв – число капель в квадрате, тогда:

π  .

 

11. ТАКОЕ РАЗНОЕ π

11.1 «π – ЧЕЛОВЕК»

 

«Пи – Человек» - так называется рассказ современного американского фантаста Альфреда Бестера. Главный герой этого рассказа вел себя странно по отношению к числам. сумму в 57075 долларов 94 цента он выбросил из окна, прокомментировав свой поступок так: «57075 – изумительное число, но 94 цента…Фу! Уродуют весь баланс». В следующий раз он получает сдачу 1997 долларов: «Ух! Выбрасываю шесть долларов из окна и наслаждаюсь оставшимися 1991».

В широком смысле π – человеком можно назвать любого математика. У.У.Сойер в книге «Прелюдия к математике» среди качеств, которыми, по его мнению, должен обладать служитель «царицы наук», на первое место ставит дерзость ума, неординарность мысли и раскрепощенность фантазии.

 

11.2 ЧЕЛОВЕК – ЦИРКУЛЬ

Согласно знаменитому канону Леонардо да Винчи, рост человека принято приравнивать к размаху его рук.

Поэт, писатель и исследователь старины Андрей Чернов полагает это распространенным заблуждением. На самом деле размах рук всегда больше роста человека. По мнению Андрея Чернова, отношение размаха рук человека к его росту равно , где Ф – число Фидия. А раз так, то число π проникает в систему древнерусских саженей – мер длины. Так, например, маховая сажень, равная размаху рук, в  раз больше ростовой сажени (роста). Используя это отношение, Андрей Чернов нашел и другие любопытные пропорции. Например, сажень большая (рост человека с поднятой рукой) так относится к ростовой сажени, как  ; косая великая сажень в  раз больше косой новгородской по трости сажени.

Как известно, системой саженей пользовались древние зодчие, возводя храмы на Руси. В частности, скрывающие число π пропорции содержит староладожская церковь Успения. Например, внутренний размах от западной стены до алтарной аспиды в π раз больше диаметра подкупольного барабана.

 

11.3 ЧИСЛА π И е – ОБЪЕКТЫ ИСКУССТВА

 

Эти числа привлекали внимание московского художника Александра Федоровича Панкина. Ниже приведены некоторые его произведения, героями которых выступают эти математические константы. В основе всех этих композиций лежит единый замысел, выражаюший четкие количественные зависимости. По номинации итальянского журнала «LUXURY Style of life» А.Ф.Панкин получил титул «Александр π».

 

 

11.4 ЧИСЛО π И ЗОЛОТОЕ СЕЧЕНИЕ

 

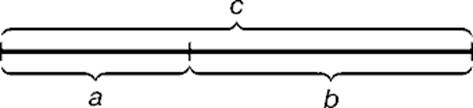
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему

 

a : b= b : c или с : b= b : а.

Свойства золотого сечения описываются уравнением: .

Решение этого уравнения:  .Больший корень этого уравнения часто обозначают буквой Ф – в честь древнегреческого скульптора Фидия., применившего золотую пропорцию при постройке Парфенона. Число Ф обладает интересными свойствами:

 

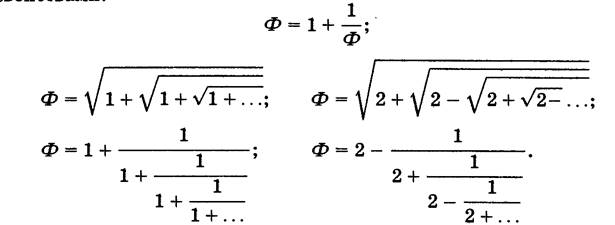
Числа  π и Ф между собой тесно связаны. Эта связь вытекает из того факта, что число Ф равно радиусу окружности, описанной около правильного десятиугольника с длиной стороны 1. О гармоничном союзе констант свидетельствуют и следующие факты:

ü  для величественного памятника пирамиды Хеопса с высокой точностью выполняются следующие соотношения: где L – длина основания, а Н – высота пирамиды

ü  закон роста красивейшей раковины Nautilus описывается уравнение золотой спирали: 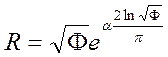, объединяющей в прекрасный букет сразу три (!)  замечательные константы.

 

 

11.5 ЧИСЛО π И СЕРЕБРЯНОЕ СЕЧЕНИЕ

 

По аналогии с золотым сеченим Андрей Чернов предлагает поименовать пропорцию, в основе которой лежит число π. А именно: точка М делит отрезок АВ в пропорции серебряного сечения, если АМ : МВ = π.

 

11.6 «МЕДНЫЙ ВСАДНИК» И СЕРЕБРЯНОЕ СЕЧЕНИЕ

 

К своим архитектурным находкам серебряного сечения А.Чернов добавил литературоведческие. Он заметил, что в поэме А.с.Пушкина «Медный всадник» 477 строк. Если это число разделить на количество строк во второй части поэмы, то получится 3,16 – число, очень близкое к π. «До 3,14 не хватает одной строки» - пишет А.Чернов.

 

 

11.7 π – ЭЗИЯ

 

Для запоминания каких-либо формул или фактов часто обращаются к мнемотехнике – системе способов, облегчающих запоминание. Многим, наверное, известна поговорка для запоминания цветов радуги: «Каждый охотник желает знать, где сидит фазан», первые букв слов в которой совпадают с первыми буквами названий цветов.

В математическом фольклоре также существует множество подобных рифм-помощников.

Три первые цифры числа  p   = 3,14… запомнить совсем несложно. А для запоминания большего числа знаков существуют забавные поговорки и стихи. Например, такие:

 

Нужно только постараться

И запомнить всё как есть:

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

                                                                            С.Бобров. ”Волшебный двурог”

 

Тот, кто выучит это четверостишие, всегда сможет назвать 8 знаков числа  p:

3,1415926…

В следующих фразах знаки числа  p    можно определить по количеству букв в каждом слове:

“Что я знаю о кругах?”   (3,1416 );

“Вот и знаю я число, именуемое Пи. – Молодец!”    ( 3,1415927 );

“Учи и знай в числе известном за цифрой цифру, как удачу примечать”                              ( 3,14159265359 )

             

 Поговорку “ Что я знаю о кругах?” предложил замечательный популяризатор науки Яков Исидорович Перельман.

Учитель одной из московских школ придумал строку:“Это я знаю и помню прекрасно”,

а его ученица сочинила забавное продолжение: “Пи многие знаки мне лишни, напрасны”.

А так выглядит 101 знак числа “ пи” без округления:            

 

3, 14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230

78164 06286 20899 86280 34825 34211 70679.

 

 

11.8 π – ШАРАДЫ

 

Догадайтесь, какие слова здесь зашифрованы?

1.   π р

2.  

3.   (π  К)

4.  

 

 

 

 

 

 

 

Ответы: пир; надпил; писк; пиво

 

 

11.9. ИНТЕРЕСНЫЕ ФАКТЫ И НЕМНОГО ЮМОРА

 

ü  Двое едут в поезде. Один говорит:

- Странно, колеса круглые, рельсы прямые, откуда стук?

- Как откуда? Колеса-то круглые, а площадь круга пи эк квадрат. Вот квадрат-то и стучит!

ü  Преподавателю одного из вузов страны придумали шутливое прозвище «Пипа». Кличка отражает одну особенность внешнего вида преподавателя. Какую? (Ответ: низкий рост. Злые языки утверждают, что рост «Пипы» равен )

ü  « - Папа, спрашивает сын отца, - почему цыплята пищат «пи-пи-пи», а когда вырастут, то «ко- ко- ко» или «ку- ка-ре-ку»?

- Наверное, потому, что пока они сидели в круглом яйце, они могли рассуждать только о нем и открыли для себя число «пи», а потом у них появились другие интересы»

 

А знаете ли вы, что:

 

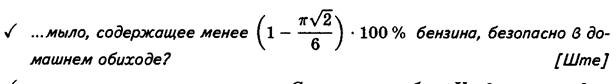
Как считают американские специалисты, это число было открыто вавилонскими магами. Оно использовалось при строительстве знаменитой Вавилонской башни. Однако недостаточно точное исчисление значения Пи привело к краху всего проекта. Возможно, что эта математическая константа лежала в основе строительства легендарного Храма царя Соломона.

 

12. p-Club ИЛИ КЛУБ ФАНАТИКОВ ЧИСЛА p

Существует один из самых необычных праздников – «День числа Пи».

В американском написании эта дата выглядит как 3.14 (3го месяца,14 числа), отсюда и объяснение, почему именно в этот день отмечается этот праздник.

Знаменательно, что праздник числа Пи совпадает с днем рождения одного из наиболее выдающихся физиков современности - Альберта Эйнштейна.

В преддверии самого замечательного праздника, дня числа Пи, отмечаемого, естественно, четырнадцатого числа третьего месяца, позвольте пригласить вас в Пи-клуб (не путать с Пиквикским и клубом любителей пива, хотя членство в них допускается). Кто же является членом самого престижного клуба. Во-первых, конечно, все Петры Ильичи, Пал Иванычи, Пулаты Ибрагимовичи и Пелагеи Иннокентьевны плюс Пироговы, Пилюлькины, Пинхасовы и Писаренки плюс любители пикников с пирожными и пирожков с пивом - они зачисляются автоматически. Так же как и пианисты, пилигримы, писатели и прочие пигмеи, вопрос о пионерах и пиратах пока не решен.

 

Знаменитые «английские круги», образованные полегшими зерновыми, снова дали о себе знать. И весьма впечатляюще. Один из восьми «узоров», обнаруженных в прошлогоднюю полевую страду в Великобритании, а именно июньский, стал известен в глобальном масштабе. Исключительно благодаря зашифрованной в нем информации и энтузиастам, обратившим на нее внимание. Круг-шифровка возник примерно в 130 километрах от Лондона, в графстве Уилтшир (Wiltshire), в местечке Barbury Castle - рядом с полем, на котором расположены останки построек доримской эпохи. На месте события побывала неутомимая исследовательница феномена Люси Прингл, сфотографировала отпечаток с вертолета и разместила снимки на своем сайте. Астрофизик из Северной Каролины (США) Михаэль Рид (Michael Reed), увидев их, понял: узор отнюдь не бессмысленный, как это обычно бывает. Его элементами зашифровано число «пи» - аж 10 знаков!

 

 

13. ЗАКЛЮЧЕНИЕ

 

Мог бы кто-нибудь сегодня удалить число π из мира дел человеческих?

Число π присутствует в чертежах и вычислениях, выполняемых электронными машинами при подготовке и проведении полетов в космос; оно предоставляет необходимое количество десятичных знаков всякий раз, когда они нужны инженерам, рассчитывающим цилиндрические, сферические или конические части машин, физикам и астрономам, когда они проводят приближенные вычисления по формулам, в которых среди фундаментальных постоянных появляется и π, как, например, в формуле для периода колебания маятника, и в тысячах и тысячах других случаев. Куда бы мы ни обратили свой взор, мы видим проворное и трудолюбивое число π: оно заключено и в самом простом колесике, и в самой сложной автоматической машине.

 

СПИСОК  ЛИТЕРАТУРЫ

1. Друянов В. «Загадочная биография Земли», 1989 г.

2. Кымпан Ф. «История числа π». М., «Наука», 1971 г.

3. Энциклопедия для детей. М., «Аванта +», 2002 г.

4. Балк М. «Математика после уроков», М., «Просвещение», 1971 г.

5. Глейзер Г. «История математики в школе», 1982 г.

6. Энциклопедический словарь юного математика.

7. Журнал «Математика в школе» № 4, 1991 г.

8. Журнал «Квант» № 3, 1980 г.

http://www.belgorod.fio.ru/studworks/transnumbers/menu_chislo_pi.htm

http://www.rg-rb.de/ch&k/2000/30/05.shtml

            http://mathc.chat.ru/hist/pihist.htm

В Сети много страниц, посвященных вычислению Пи, отмечу лишь, что на http://www.cs.unb.ca/~alopez-o/math-faq/mathtext/node12.html   расположена программа, написанная Диком Т. Винтером (Dik T. Winter at CWI) на Си всего 160-ю символами, но вычисляющая 800 знаков Пи!

На http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibpi.html   лежит статья о связи чисел Фибоначчи с числом Пи

 

Страница http://www.algonet.se/~eliasb/pi/binpi.html   посвящена представлению цифр числа Пи в двоичной форме. Там же можно найти невероятные картины, сформированные этими двоичными числами

 

Если вы хотите узнать, с какой цифры числа Пи встречается дата вашего рождения, то зайдите на http://www.facade.com/legacy/amiinpi/ введите дату (сначала месяц, потом день) и получите ответ, можете использовать его для паролей :)

Интересные адреса на русском языке:
История вычисления числа Пи и алгоритмы этих вычислений
И здесь тоже, но чуть другие материалы.
Перечень курьезных законов, в штате Индиана Пи=4
Стишок для запоминания цифр числа Пи   и его обсуждение Знатоками на Волге
Занимательные штучки, связанные с числом Пи, в том числе и фильм про него.
О фильме про число Пи

Ну а если вы зайдете на http://3.14159265358979323846264338327950288419716939937510582097.org/   то откроется поисковик Googl с ссылками на ресурсы о числе Пи

Скачано с www.znanio.ru