Исследовательский проект по теме "Объёмы"

КИРОВСКОЕ ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ АВТОНОМНОЕ УЧРЕЖДЕНИЕ

«ТЕХНИКУМ ПРОМЫШЛЕННОСТИ И НАРОДНЫХ ПРОМЫСЛОВГ. СОВЕТСКА»

 

 

 

 

 

 

 

ОБЪЁМЫ ТЕЛ

 

 

 

 

 

 

 

 

 

Автор: Сухих Сергей

студент группы№ 26,

профессия «Автомеханик»

Руководитель:

Чернова Ирина Николаевна,

преподаватель математики

«Техникум промышленности и

народных промыслов

г. Советска»

 

 

 

Советск, 2018

 

СОДЕРЖАНИЕ

 

1.     Введение.……………………………………………………………………...3

2.     Задача про чайники………………………………………………………...4-5

3.     Из истории объемов тел……….……………………………………………..6

4.     Определение объема и его свойства…………..…………….........................7

5.     Формулы объёмов тел вращения и многогранников…………………...8-12

6.     Задачи……………………………………………………………….....…13-16

7.     Выводы………………………………………………………………………17

8.     Использованные ресурсы……………………………………………….......17

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

 

В 2015 году я закончил 9 классов и поступил учиться в «Техникум промышленности и народных промыслов» города Советска. На 2 курсе я начал посещать математический кружок «УМКа», на котором мы занимаемся проектной деятельностью. Нам было предложено много тем, но я остановился на теме «Объемы». Выбор моей темы был неслучайным: дома сломался чайник, и прежде чем купить новый, мне захотелось узнать, какой геометрической формы должен быть чайник, чтобы вода в нем остывала как можно дольше.

Гипотеза 1: процесс остывания воды в чайнике не зависит от формы чайника.

Гипотеза 2: знание формул объёмов тел и многогранников необходимо для решения практических и производственных задач

Предмет исследования: геометрические тела и многогранники их объёмы.

Объект исследования: наука – математика.

Методы исследования: поиск информации, её анализ, отбор, обобщение.

Проектный продукт: презентация и статья (реферат).

Перед собой я поставил цель: обобщить и систематизировать знания по объемам тел и многогранникам и убедиться в практической значимости математики.

Задачи:

1.     Узнать историю объёмов тел.

2.     Систематизировать и обобщить знания по объёмам тел и многогранников.

3.     Показать применение формул объёмов для решения практических задач.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

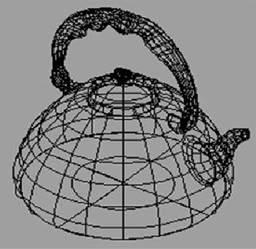
Форма чайника и процесс остывания воды

Задание: какой геометрической формы должен быть чайник, чтобы вода в нем остывала как можно дольше?

Цель: убедиться в практической значимости математики

Известно: чем меньше площадь полной поверхности чайника, тем дольше остывает в нем вода.

Дано: V = 3 л          

Найти: S

Решение:

 R ≈ =  = 0.9

S = 4πR² = 12 × 0.81 ≈ 9.6

S ≈ 9.6 дм²

Дано: V = 3л

Найти: S

Решение:

V = πR³ 3 = 2R³ R ≈  =  = 1.2

S = πR² + 2πR² = 3πR² ≈ 9×1.44 ≈ 13

S ≈ 13 дм²

 

Дано: V = 3л

R = 0.9 дм r = 0.8 дм

Найти: S

Решение:

V = πH(R²+rR+r²) 3 ≈ H × (0.81 + 0.72+0.64) H ≈ ≈ 1.38

l =  ≈  =  ≈ 1.4

S = π × (R + r) × l + πR² + πr² ≈ 3×1.7×1.4+3×0.81+3×0.64≈11.5 дм²

S ≈ 11.5 дм²

 

Дано: V = 3л; H = 2 дм

Найти: S

Решение:

V = πr²HR² =  ≈  = R ≈  ≈ 0.7

S = 2πR² + 2πRH = 2πR × (R + H) ≈ 6 × 0.7 × 2.7 ≈ 11.3

S ≈ 11.3 дм²

 

 

 

 

Сравним полученные результаты

 

Вид чайника	V	S
Шаровой	3л	9,6
Полу-шаровой	3л	13
Цилиндрический	3л	11,3
Конический	3л	11,5

 

Вывод: шаровой чайник остывает медленнее, чем чайник того же объема любой другой формы. Таким образом,  моя гипотеза о том, что процесс остывания воды в чайнике не зависит от формы чайника, не подтвердилась. Но я убедился в практической значимости математики и перешёл к решению следующих поставленных задач, а именно: систематизировать и обобщить знания по объёмам тел и многогранников, применять их к решению практических задач.

 

 

 

 

История создания объемов тел

Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука. Примерно в VI - V вв. до н. э. в Древней Греции в геометрии начался новый этап развития, что объясняется высоким уровнем, которого достигла общественно-политическая и культурная жизнь в греческих государствах.

      В древнеегипетских папирусах, в вавилонских клинописных табличках встречаются правила для определения объема усеченной пирамиды, но не сообщаются правила для вычисления объема полной пирамиды. Определять объем призмы, пирамиды, цилиндра и конуса умели древние греки и до Архимеда. И только он нашел общий метод, позволяющий определить любую площадь или объем. Идеи Архимеда легли в основу интегрального исчисления. Сам Архимед определил с помощью своего метода площади и объемы почти всех тел, которые рассматривались в античной математике. Он вывел, что объем шара, составляет две трети от объема описанного около него цилиндра. Он считал это открытие самым большим своим достижением. Среди замечательных греческих ученых V - IV вв. до н.э., которые разрабатывали теорию объемов, были Демокрит и ЕвдоксКнидский.

       Объем — это вместимость геометрического тела, т. е. части пространства, ограниченной одной или несколькими замкнутыми поверхностями. Вместимость или емкость выражается числом заключающихся в объеме кубических единиц. На Руси в старину использовались в качестве единиц измерения объёма ведро (около 12л), штоф (десятая часть ведра). В США, Англии и других странах используются баррель (около 159л), галлон (около 4л), бушель (около 36л), пинта (от 470 до 568 кубических сантиметров).

Для удобства решения задач, в физике объем принято  измерять в м³. Кубический метр (название говорит само за себя) —  это куб, высота, длина, ширина которого равна 1 метр. В химии, чтобы определить количество веществ в газе, используется молярный объем. До введения метрической системы для измерения малых объемов жидкости применяли унции. Одна унция соответствует 29,573 мл вещества. Широко использовали эту меру в парфюмерной промышленности и аптеках. В мире современных технологий удобно пользоваться онлайн конвертером единиц, он поможет решить задачку по физике, химии, а молодым хозяйкам правильно измерить объём ингредиентов при приготовлении блюда.

 

 

Определение и свойства

Определение:

 

Объемом называется положительная величина, характеризующая часть пространства, занимаемую телом.

 

Свойства:

 

•      Объем тела есть неотрицательное число;

•      Если геометрическое тело составлено из геометрических тел, не имеющих общих внутренних точек, то объем данного тела равен сумме объемов тел его составляющих;

•      Объем куба, ребро которого равно единице измерения длины, равен единице;

•      Равные геометрические тела имеют равные объемы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Объем куба

Объем куба равен кубу длины его ребра.

 

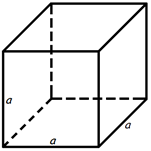
Формула объема куба:V = a³

 

где V - объем куба, 
a - длина ребра куба.

 

Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.

 

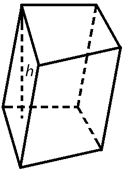
Формула объема призмы:V = S_o h                

 

где V - объем призмы, 
S_o - площадь основания призмы, 
h - высота призмы.

 

 

 

 

 

 

Объем параллелепипеда

Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

 

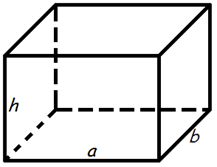
Формула объема прямоугольного параллелепипеда:V = a · b · h

 

 

где V - объем прямоугольного параллелепипеда, 
a - длина, 
b - ширина, 
h - высота.

 

Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.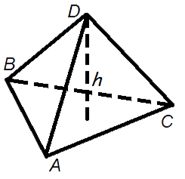

Формула объема пирамиды:

V =	1	So · h
	3

 

 

где V - объем пирамиды, 
S_o - площадь основания пирамиды, 
h - длина высоты пирамиды.

 

 

 

Объем правильного тетраэдра

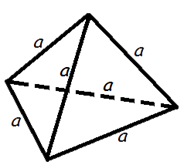
Формула объема правильного тетраэдра:  V =	a3
	12

 

где V - объем правильного тетраэдра, 
a - длина ребра правильного тетраэдра.

 

 

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

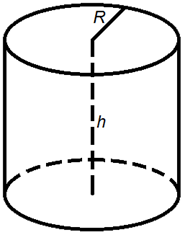
Формулы объема цилиндра:

• V = π R² h
• V = S_o h

 

где V - объем цилиндра, 
S_o - площадь основания цилиндра, 
R - радиус цилиндра, 
h - высота цилиндра, π = 3,141592.

Объем конуса

Объем конуса равен трети от произведения площади его основания на высоту.

 

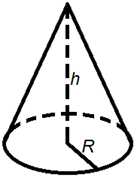
Формулы объема конуса:

V =	1	π R2 h
	3

 

V =	1	So h
	3

 

где V - объем конуса, 
S_o - площадь основания конуса, 
R - радиус основания конуса, 
h - высота конуса, 
π = 3,141592.

 

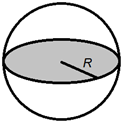
Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

 

Формула объема шара:   V =  4 π R3 3 где V - объем шара,  R - радиус шара, π = 3,141592.

 

Объем усеченной пирамиды

 

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S1(abcde), нижнего основания усеченной пирамиды S2(ABCDE) и средней пропорциональной между ними.

 

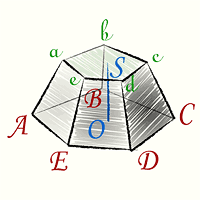
Формула объема усеченной пирамиды:

 

V=h(S1 + + S2 )

 

где S1 – площадь верхнего основания усеченной пирамиды, S2 – площадь нижнего основания усеченной пирамиды, h–высота усеченной пирамиды.

 

 

 

 

 

 

Объем усеченного конуса

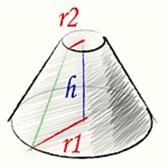
Объем усеченного конуса вычисляется по следующей формуле:

 

V =πh (r₁² + r₁ ×r₂ + r₂² )

 

 

Где r1 – радиус нижнего основания усеченного конуса; r2–радиус верхнего основания усеченного конуса; h – высота усеченного конуса

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачи

 

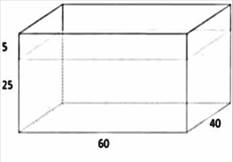
1.     Сколько ведер воды по 8 литров каждое, налито в аквариум, изображенный на рисунке.

 

 

Мы знаем, что 1 литр = 10 куб.дм.

1.      25-5 = 20 (см) – высота налитой воды.

2.      20*40*60 = 48000 (куб. см) – объём воды в аквариуме.
48000 куб. см = 48 куб. дм = 48 литров

3.      48:8 = 6 (вед.) – воды потребуется.

 

Ответ: 6 ведер.

 

 

2.     Классные помещения должны быть рассчитаны так, чтобы на одного учащегося пришлось не менее 6 м³ воздуха. Размера кабинета математики составляют 9*8.7*2.8. Можно ли заниматься в таком помещении 30 студентам, не нарушая санитарные нормы?

V = 2,8∙9∙8,7 = 219,24 м³

219,24/30 = 7,3 м³

Ответ: можно

 

 

3.     Котел имеет форму полушара диаметром 60см. Определите ёмкость котла.

V_м = π * 27 = 36π дм³

V=  = 18πдм³ = 18*3,14 = 56,5

Ответ: 56.5 литров.

 

4.     Объем раствора в гальванической ванне равен 3 куб. м, при этом уровень раствора достигает высоты 75 см. В ванну погрузили деталь, после чего уровень раствора поднялся на 2 см. Найдите объем детали (в куб. м).

 

За основу берется формула 

 

Объем раствора в гальванической ванне можно найти по формуле:

 

Объем детали погруженную  в эту же ванную находим по этой же формуле:

 

Сделаем необходимые преобразования:

Из первой формулы  и подставим во вторую

Ответ: 0,08

 

5.     В цилиндрический сосуд налили 3000 см³ воды. Уровень воды при этом достиг высоты 20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 3 см. Чему равен объем детали? Ответ выразите в см³

 

При решении данной задачи можно воспользоваться  утверждением: Объем налитой воды в сосуд прямо пропорционален уровню ( высоте ) воды в данном сосуде, при условии, что  величина постоянная.

 

3000 см³ – 20 см

   х см³   -   3 см

х = (3000∙3):20

х = 450Ответ:450

 

6.     Коническая куча зерна имеет высоту 2.4м, а окружность основания 20м. Сколько тонн зерна в куче, если масса одного кубометра равна 750кг?Сколько рейсов нужно сделать водителю автомобиля ГАЗ-53-12, чтобы перевезти эту кучу зерно на элеватор, если вместимость кузова  4.5 тонн.

 

Решение:

 

h = 2,4м     С = 20м                                 19,2/4,5 = 4,26 = 5 рейсов

C = 2πr

10 = πr

r =  ≈ 3,2м

V_к = πr²h =  ∙ 3,14 ∙ 3,2² ∙ 2,4 = 25,7м³

25,7 ∙ 750 = 19275кг = 19,275т                         

Ответ: 5 рейсов

 

 

 

7.     Диаметр поршня автомобиля МАЗ равен 130мм, ход поршня Н₁ = 140 мм. Высота камеры сгорания Н₂ = 9мм. Найдите рабочий и полный объём двигателя с 6 цилиндрами.

Дано: двигатель МАЗ

Д = 130 мм, Н₁ = 140 мм,H₂ = 9мм, n = 6

Найти: рабочий объём двигателя V_р

Решение:

V_p=∙ Н₁ ∙n;V_p =  ∙ 13 ∙ 4 = 6898,58см³≈ 6,9дм³ = 6,9л

H = H₁+H₂ = 14 + 0,9 = 14,9см

V_п =  ∙ H ∙ n; V_п =  ∙ 14.9 ∙ 4 = 7906,834см³ = 7.9дм³ = 7.9л

Ответ: V_р = 6,9л; V_п = 7,9л

Умение находить рабочий объём двигателя важно для автослесаря.  Величина рабочего объёма двигателя зависит от диаметра цилиндра и величины хода поршня, влияет на увеличения расхода топлива, а также увеличение  мощности двигателя.

 

 

ВЫВОДЫ

 Объем очень важное математическое понятие, которое постоянно встречается в повседневной жизни. Моя гипотеза о том, что знание формул для нахождения объёмов тел и многогранников необходимо для решения практических задач, подтвердилась. Работая над проектом, я обобщил и систематизировал знания по теме: «Объёмы». Уверен, что это мне пригодится при подготовке к экзамену, а также и в профессиональной деятельности.

 

 

 

 

ИСПОЛЬЗОВАННЫЕ РЕСУРСЫ

 

1.     http://ru.onlinemschool.com/pictures/volume/cube.png

2.     http://www-formula.ru/index.php/2011-09-24-00-37-25

3.     https://uztest.ru/abstracts/?idabstract=216487

4.     https://uztest.ru/abstracts/?idabstract=757154

5.     https://infourok.ru/issledovatelskaya-rabota-na-temu-prakticheskoe-primenenie-obemov-1133430.html

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Скачано с www.znanio.ru