Спецификация

1.      Назначение работы:  определение уровня достижения планируемых результатов освоения обучающимися учебного курса «Алгебра и начала математического анализа» для 11 класса на углубленном уровне.

2.      Документы, определяющие содержание работы:

-Федерального государственного образовательного стандарта среднего общего образования от 18.05.2023 Приказ № 371

-Федеральная рабочая программа среднего общего образования. Математика. Углубленный уровень.

-Положение о формах, периодичности и порядке текущего контроля и промежуточной аттестации обучающихся. 

3.      Форма промежуточной аттестации: итоговая контрольная работа

4. Структура  работы: 2 варианта

Всего в работе 20 заданий, среди них 10 заданий обязательного уровня и 10 заданий повышенного уровня освоения курса, сгруппированных попарно и обозначенных буквами А (базовый уровень) и Б (повышенный уровень).

Таким образом, каждое предметное умение представлено заданием и на базовом, и на углубленном уровне. Это дает обучающемуся возможность выстроить собственную стратегию выполнения работы. В зависимости от уровня подготовки он может в каждом случае выбирать, какие задания он будет выполнять А или Б, конечно же, он может выполнять все задания в любой последовательности, его цель – выполнить как можно больше заданий и набрать как можно больше баллов.

Кодификатор

Табл. 1. Распределение заданий по разделам содержания

План контрольной работы приведен в таблице 2. Сокращения: Б – базовый уровень, П – повышенный уровень.

Табл. 2. План варианта работы

5.      Продолжительность работы: 90 минут

6.      Система оценивания 

Табл. 3. Рекомендации по оцениванию выполнения контрольной работы

7. Ключ к контрольно-измерительным материалам

Итоговая контрольная работа по курсу «Алгебра и начала математического анализа. Углубленный уровень». 11 класс

Вариант 1

1.А) Разложите на простые множители 675.

Б) Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число делилось на 18. В ответе укажите получившееся число.

2.А) Найдите сумму комплексных чисел 𝑧₁ = 1,3 − 2,5𝑖 и  𝑧₂ = −0,5 − 2,3𝑖     Б) Выполните действия:  (3 + 2𝑖) ∙ (2 − 3𝑖) + (3 − 2𝑖)

3.А) Решите неравенство:

Б) Решите неравенство log₂(3х + 1) ≤ log₂(х + 2). В ответ запишите количество целых    решений.

                                                                              2х − у = 1;                                                             ²х ^{+ 2у = 6;}

4.  А) Решите систему уравнений:{5_{х + У = 25.}   Б) Решите систему уравнений: ^{₂х _{− 2у = 2.}

5.  Определите по графику:

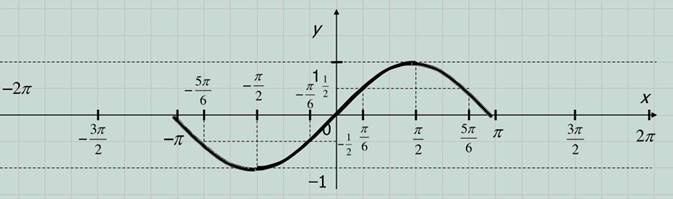
А) промежутки монотонности функции на данной области определения;

Б) все, принадлежащие отрезку [–  π; π] корни уравнения 𝑠𝑖𝑛𝑥 = .

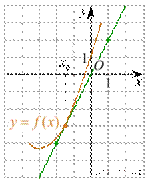
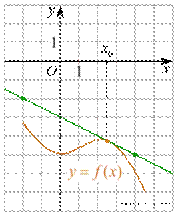
6.А) На рисунке изображён график функции и касательная к нему в точке с абсциссой x0.   Найдите значение производной функции f(x) в точке x0.

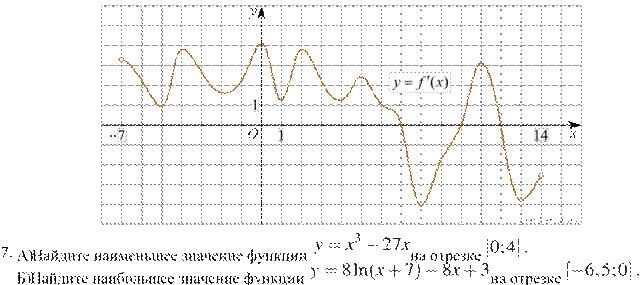
Б) На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14).

Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

8.      А)Найти первообразную функции  в общем виде: у = 4х – 5.

    Б)Найти первообразную функции, график которой проходит через точку М: у = х + 2, М(2; 7). 

9.      А)Вычислить интеграл: .  

    Б)Найти площадь криволинейной трапеции: у = 2х, у = 0, х = 0, х = 2.  

10.  А)Решите уравнение: 𝑎(𝑎 − 3)𝑥 = 𝑎 − 3

Б)При каких значениях параметра а уравнение (𝑎 + 1)𝑥² − (2𝑎 − 3)𝑥 + 𝑎 = 0 имеет два корня?

Итоговая контрольная работа по курсу «Алгебра и начала математического анализа. Углубленный уровень». 11 класс

Вариант 2

1. А) Разложите на простые множители 756.

    Б) Вычеркните в числе 123456 три цифры так, чтобы получившееся трёхзначное число делилось на 27. В ответе укажите получившееся число.

2.А) Найдите сумму комплексных чисел 𝑧₁ = 0,6 − 2,1𝑖 и  𝑧₂ = −4,5 − 1,3𝑖 Б) Выполните действия:(4 + 3𝑖) ∙ (−3𝑖) + (3 − 4𝑖) ∙ (4𝑖)

3.А) Решите неравенство:

   Б) Решите неравенство 3^х+2 - 3^х < 24. В ответ запишите наибольшее целое решение

4.  А) Решите систему уравнений:{х +х у = 1;      Решите систему уравнений:{          3х + 5у = 8;   

                                                                                 2 ^−у = 8. ^Б)                                                        ₃^х − 5^у = ₋2_.

5.  Определите по графику:

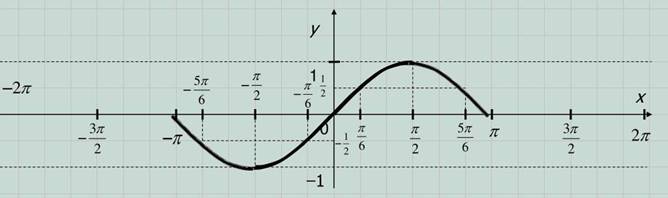
А) промежутки знакопостоянства функции на данной области определения; Б) все, принадлежащие отрезку [–  π; π] корни уравнения 𝑠𝑖𝑛𝑥 = − .

6.А) На рисунке изображён график функции и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

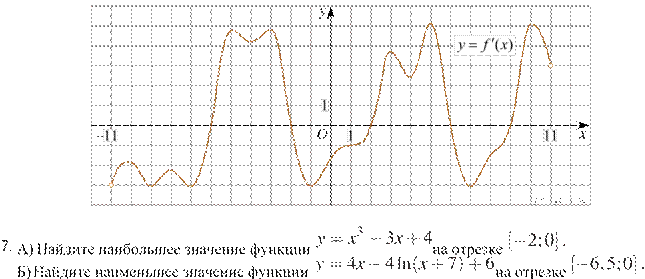
Б) На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11).

Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

8.А) Найти первообразную функции  в общем виде: у = х – 3.

   Б) Найти первообразную функции,  график которой проходит через точку М: у = 1 + 3х, М(2; 9)

9.А) Вычислить интеграл .

   Б) Найти площадь криволинейной трапеции: у = х + 1, у = 0, х = −1 , х = 1.

10.А) Решите уравнение: 2𝑎(𝑎 − 2)𝑥 = 𝑎 − 2

     _Б) При каких значениях параметра а уравнение (𝑎 + 1)𝑥² − (2𝑎 − 3)𝑥 + 𝑎 = 0 не имеет корней?