Из опыта работы. Ассоциации в математике

Ассоциативное мышление на уроках математики

Мышление начинается с удивления.

Аристотель

Невысокий уровень знаний у учеников по математике является одной из главных проблем математического образования в общеобразовательной школе. Чтобы добиться положительного результата, необходимо найти средства и методы обучения, соответствующие особенностям развития детей.

Дело в том, что школьники целиком зависят от определенной ситуации, а это накладывает отпечаток на получаемые знания: в большинстве своем они не систематизируются и ограничиваются личным чувственным опытом.  Известно, что мы запоминаем лишь те события, которые у нас вызвали какие-либо эмоции: удивление, радость, сопереживание, волнение, гнев и другие.

Немаловажную роль для достижения положительного результата играет развитие и формирование мыслительных процессов, развитие памяти.

Т.о. на уроках математики стала использовать приемы  ассоциативного мышления. Формулы, правила легко можно воспроизвести, если построить ассоциативный ряд. Умение правильно и верно составлять ассоциативные связи между словами – залог быстрого запоминания и качественного развития памяти.

Алгебра

Множество чисел

1.     Натуральные числа – натура - можем взять в руки и подсчитать;

2.     Целые числа – цельные – без дробей;

3.     Иррациональные числа – неразумные числа – ускользающие – не знаем  сколько в руках.

4.   Число .

1)   

22 совы скучали

                На больших 7 суках

               22 совы мечтали

               О семи больших мышах,

               О мышах довольно юрких,

               В аккуратных серых шкурках.

2)    3,1415926 (три четырнадцать пятнадцать девяносто два и шесть)

3)    3,1416 (что я знаю о кругах- количество букв в слове)

4)    3,14159265358 (это я знаю и помню прекрасно пи лишние
знаки тут чужды напрасны – количество букв в слове)

Сравнение чисел. Знак неравенства

У знака неравенства на нижней  линии поставить штрих. Получили число 4 – знак меньше, число 7 – знак больше.

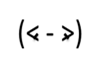
Правила сложения чисел

1.     Знаки одинаковые – складываем, ставим их знак;

2.     Знаки разные – вычитаем, ставим знак большего числа.

Распределительный закон  умножения

·        ab+ac=a(b+c)

Находим солнышко с и выносим его за скобки, на улицу.

·        a(b+c)=ab+ac

Папа а дает фамилию своим детям, когда они выйдут из дома - скобки, то к имени добавляется фамилия а.

Правило раскрытия скобок

Пришел в гости + - добрый знак, знаки в доме – скобке не меняются;

Пришел в гости «−» - зловредный знак, знаки в доме – скобке меняем на противоположные.

Алгоритм решения уравнений

Неизвестные живут слева, известные справа. На ночь идут домой, если переходят через мост - равно – знак меняется, если сидит дома, то знак сохраняется.

Свойства степени

(aⁿ)^m – числа m и n находятся рядом, значит умножаем.

Формулы сокращенного умножения

(а+b)²=a²+2ab+b² – волшебная формула, волшебство – 2ab

Числовые промежутки

(а; b: в числе а – пропасть – точка выколота, дыра (мы не можем ее взять), скобка – круглая – скользкая;

: в числе а – мост - закрашиваем (мы можем зайти на него, взять число),

скобка – квадратная, ручку – рисуем.

Неравенства с модулем

Используем геометрический смысл модуля. Модуль – расстояние от точки 0 до точки с координатой, которое равно а, следовательно мы можем ходить от 0 влево и вправо на а шагов, получим две точки а и –а.

1.   - ходим внутри интервала от  −а до а, получаем двойное неравенство –а<x<a

2.    - ходим вне интервала, получаем два промежутка, следовательно, нужно решить совокупность неравенств

Графики функций

1.     Абсцисса – икс (все звуки шипящие), ордината – игрек (Р-р-ычим)

2.   у= – лежащая ветка параболы.

3.   у=  – галка.

4.     Движение графиков функций. y=f(x+l) +m. Движение по оси х (шипящий – змея, зловредный – перемещаемся с точностью наоборот, l>0 – в минус, l<0- в плюс). Движение по оси у – игрек – Р-родной, все хорошо- m>0 – движение в плюс, m<0- в минус)

5.     Построение кусочной функции

Функция живет только в своем государстве (условие – если), за границу не выезжает.

6.     Возрастающая функция – график поднимается в гору.

7.     Убывающая функция – по графику катимся с горы.

8.      График производной функции – фиксируем точки пересечения графика с осью  х – точки экстремума функции.

Геометрия

Луч

Луч солнца, солнце  – начало - главная точка для нас, название луча начинается с точки начала луча.

Вершина угла АОВ

Точка вершины угла – О – босс, его всегда охраняют, поэтому он находится посередине, охрана А и В  может меняться местами.

Площадь и периметр

Площадь – Красная, солдаты на параде занимают  каждый кирпич, значит нужно найти количество кирпичей, умножить длину на ширину.

Периметр – солдаты охраняют здание по периметру, значит нужно найти длину охраняемой зоны.

Формула площади треугольника

Параллелограмм – главная фигура, треугольник  – его половина,  следовательно, в формуле площади будет коэффициент .

Практика показывает, что ученики через несколько лет после изучения темы, вспоминают ее только через ассоциации. Ученики, у которых развито  ассоциативное мышление, которые сами могут придумывать ассоциации, имеют возможность применить полученные навыки, как  на других предметах, так и в повседневной жизни.