Снигирева Людмила Николаевна магистр по направлению подготовки

 44.04.01 Педагогическое образование  Учитель математики и физики первой квалификационной категории

МКОУ «Лицей №7 имени Шуры Козуб с. Ново-Ивановского» 

Майского муниципального района, КБР

Людмила Снигирева <[email protected]>

Тематическое направление: обучение математике с учетом образовательных потребностей и способностей обучающихся

К ВОПРОСУ О ВЗАИМОДЕЙСТВИИ ОСНОВНОГО И

ДОПОЛНИТЕЛЬНОГО МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ КАК

ЭФФЕКТИВНОЙ РАБОТЫ С ОДАРЕННЫМИ ШКОЛЬНИКАМИ

Аннотация: в данной статье рассматривается вопрос развития одаренных детей через организацию познавательной деятельности на уроках математики путём решения заданий метапредметной направленности. Формирование метапредметных результатов обучения происходит как на уроках математики, так и во вне урочной деятельности. Методологические идеи обновленных образовательных

стандартов позволяют предположить, что именно реализация межпредметных связей в процессе преподавания учебных предметов, в частности математики и физики на уроках математики может создать почву для взаимодействия основного и дополнительного математического образования на уровне познавательного интереса.

Ключевые слова: мотивирующие вопросы, цифровое оборудование, математики, физики, эмоциональный интеллект.

Учитель, работающий в современной школе, должен понимать, какие принципиально новые дидактические подходы к уроку регламентирует Федеральная Основная Образовательная Программа (ФООП). Одной из приоритетных целей стали сохранение глубины и фундаментальности отечественного образования и обеспечение лидирующих позиций России в области фундаментального математического образования … и др. прикладных наук [5]. Дополнительные условиями стандартов рассчитаны на то, что они должны обеспечить единство образовательного пространства России; развитие личностных качеств; единство учебной и воспитательной деятельности; формирование культуры непрерывного образования и саморазвития на протяжении всей жизни; разумное и безопасное использование цифровых технологий [6].

В этой связи духовно-нравственные  позиции  философско-педагогической  концепции ведущих педагогов прошлого таких как В.А. Сухомлинского и К. Д. Ушинского актуальны и особо значимы. В 1947 г  Павлышской «Школе радости», где Сухомлинский В.А. служил директором много лет, считал, что необходимо следующее педагогическое условие: «Воспитание  заключается  в  том,  чтобы  умело,  умно,  мудро, тонко, сердечно прикоснуться к каждой из тысячи граней, найти ту, которая, если ее, как алмаз, шлифовать, засияет неповторимым сиянием человеческого  таланта,  а  это  сияние  принесет  человеку  личное  счастье» [1, с. 14]. Ранее в 1854 г. Ушинский К. Д., инспектор Гатчинского сиротского института,   утверждал, что если возбудить в ребенке искренний интерес ко всему полезному, высшему и нравственному, то это поможет сохранить человеческое достоинство на постоянной основе. [7].

На сегодняшний момент, в рамках национального проекта «Образование»,  действуют центры образования «Точка роста» с целью развития у обучающихся естественно-научной, математической, информационной грамотности, формирования критического и креативного мышления, совершенствования навыков естественно-научной направленности, а также для практической отработки учебного материала по учебным предметам «Математика», «Физика», «Химия», «Биология», «Информатика». Современное техническое и цифровое оборудование центров позволяет развивать внимание ученика используя восприятие всех органов чувств: зрения и слуха с помощью мультимедийных  технологий; обоняния, эстетического вкуса, осязания при использовании цифровой лаборатории самостоятельно. Это великолепные центры «Школы радости» В.А. Сухомлинского и научных идей К. Д.

Ушинского, в которых обучаются одаренные дети. 

Учитывая интересы и запросы обучающихся и их родителей (законных представителей) и данные мониторинговых исследований, следует отметить, что уровень развития интеллектуальных (интерес к окружающей действительности) и творческих способностей (активное использование воображения, фантазии и образного мышления), свободное взаимодействие в коллективе требует определенных методических нововведений и педагогических технологий для роста и развития. В связи с этим, выделим три категории одаренных детей и рассмотрим таблицу 1«Одаренные дети в системе уровневого подхода в обучении».

В таблице 1 учтены три направления требований к результатам изучения математики Концепции развития математического образования в Российской

Федерации [3]. Практическое внедрение основных идей Концепции и обновленных ФГОС ставит перед системой образования проблему формирования эмоционального интеллекта обучающихся в принятых  примерных рабочих программах по каждому предмету  в  разделе  «Метапредметные  результаты».  Под  эмоциональным  интеллектом  понимается  «способность  распознавать  и понимать свои эмоции и эмоции других людей, управлять ими и использовать эмоции для  решения  задач  и  достижения  результатов»  (Д.  Майер,  П.  Сэловей),  т.е.  это способность быть компетентным в человеческих контактах и понимать себя [4].

Познавательный интерес как эмоция получения новой информации лежит в основе позитивного отношения к жизни вообще и к учёбе в частности. Если у человека сформирован такой интерес, то человек активно ищет ответы на вопросы, которые сам себе задаёт. Соответственно,  одним  из  путей  повышения эффективности учебной деятельности могут быть мероприятия по развитию эмоционального  интеллекта  обучающихся,  поскольку  они  более мотивированы  к  учебе  и  выполнению  учебных  заданий. Поэтому система вопросов для развития эмоционального интеллекта позволяет  проводить  занятия  на  уровнях, вызывающих  творческое состояние у  разных  детей,  успевающих  по-разному,  в этом проявится индивидуализация и дифференциация обучения. Таким образом, образовательная задача  взаимодействия основного и дополнительного математического образования состоит в создании условий, провоцирующих детское действие на метапредметном уровне, т.е. за пределами учебного предмета.

Таблица 1.

Классификация «Одаренные дети в системе уровневого подхода в обучении».

Исходя из опыта двадцатилетней работы с одаренными детьми, предлагается следующая методическая система:

1.   Мотивирующие вопросы на уроке.

2.   Проектная деятельность на дополнительных занятиях.

3.   Обобщение темы с применением учебных карт действий.

Приведем пример системы заданий по теме: «Производная» в 10 классе.

1. Как сформировать систему мотивирующих вопросов на уроке.

Одним из условий повышения эффективности учебного процесса и совершенствования качества знаний учащихся является установление и реализация межпредметных связей в процессе преподавания учебных предметов, в частности математики и физики. Взаимосвязь учебных предметов физики и математики отражает взаимосвязь наук физики и математики, которая определяется наличием у них общей предметной области.

Например, в 10 классе производная используется при рассмотрении некоторых вопросов электродинамики. Но особенно широко математика используется в курсе физики 11 класса. Это выражается в систематическом применении производной при изучении колебаний, использовании и закреплении свойств тригонометрических и показательной функций, использовании интегрирования при решении задач (радиоактивный распад, поглощение излучений, и т.п.).

Это не простое применение математики, а развитие и конкретизация её идей и методов на широком естественнонаучном материале. Кроме того, при изучении физики происходит формирование и развитие ряда математических предметных УУД (универсальные учебные действия) как в технике вычислений, так и в области графических и аналитических умений. Пример, такого типового задания на Формирование умения проводить теоретическое исследование «работа с информацией» на уроке 10-11 класса по теме: «Производная», рассмотрен в Приложении 1.

Цель: формирование умения оценивать факты, события, явления и процессы с помощью разных критериев, выделять причинно-следственные связи.

Форма учебно-познавательной деятельности: работа индивидуальная и в группах по 4—5 человек.

Описание задания: учащимся предлагается провести теоретическое исследование. Теоретическое исследование – это формулирование общих закономерностей, позволяющих объяснить ранее открытые факты и эмпирические закономерности.

Материал: текст на карточке.

Мотивирующие вопросы:

Рисунок 1

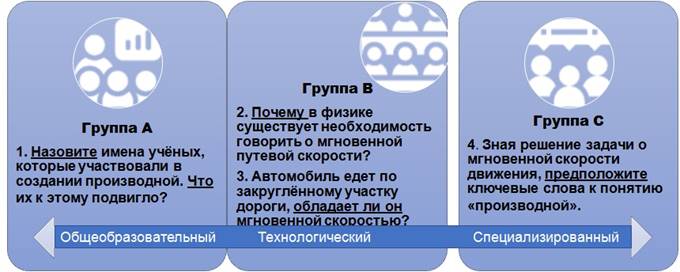
Для того, чтобы ответить на вопросы, учащимся нужно вспомнить (прочитать), что необходимо знать, чтобы понимать производную функции, описать движение тела по закруглённому участку дороги, сравнить две задачи о «разыскании» и определить общие слова к понятию «производной». 

Примечание: задачу можно решать при создании на уроке математике проблемной ситуации (на уроке – изучение нового материала, работая в парах по 2 человека, как и,  при проведении обобщающего урока).

2. Как привлечь одаренных детей к дополнительным занятиям.

Акцент делается не на получение отвлеченных от жизни знаний, а на необходимости познания окружающего мира, подготовке ребенка к различным жизненным ситуациям, на отработке умения находить полезную информацию и применять ее в реальной жизни.

В конце урока учащимся предлагается тема «Мини-проекта» с использованием комплекта «Цифровое оборудование по математике», (см. табл. 2) с мотивирующими вопросами изучения  темы Производной на практическом уровне.

Т.о. главным  является  то,  что  цифровые  лаборатории способны  заменить  огромное  количество  традиционных  приборов.  Процесс получения знаний становится более интегрированным. 

Таблица 2. 

Межпредметный проект.

Проектно-исследовательская деятельность по естественнонаучным и математическим дисциплинам имеет наибольшую эффективность в дополнительном математическом образовании, особенно в форме интегрированных проектов. Поэтому при организации внеурочной деятельности одновременно хорошо спланировать тему изучения экспериментальной работы «Измерение магнитной индукции» (см. Приложение 2). При правильной организации деятельности на уроке такого вида у учащихся развивается любознательность, смекалка, креативное мышление, чувство ответственности и эстетический вкус. Изящно выполненная работа способствует развитию чувства красоты, удовлетворённости от проделанной работы.  

3. Обобщение темы с применением учебных карт действий.

Для урока, на котором проводится обобщение данного вида деятельности и составление обобщённой схемы, необходимы специально подготовленные дидактические материалы. Пример учебной карты действий по созданию понятия о производной через анализ и обобщения накопленных данных в ходе теоретического исследования предложен в Приложении 3[2]. Во первых, это схемы (таблицы) деятельности в конкретных ситуациях, выполнявшиеся учащимися на уроках предварительного этапа освоения деятельности.  Во вторых, поскольку процесс формулирования обобщённых шагов схемы достаточно труден, учащиеся должны получить «подсказки» — россыпь фраз с названием этих шагов. Такая россыпь готовится для каждого ученика и помещается в конверт. Другой вариант – выдать учащимся распечатанную в произвольном порядке россыпь фраз с заданием сделать дома и принести её на урок.

При этом если ребёнок увлечён, то создаётся ситуация успеха, школьник испытывает эмоциональный подъём, радуется собственным познаниям и своей удачи от решения вопроса. Такой вид компетенции особо эффективно развивается, когда организация процесса усвоения этих схем (таблиц деятельности) способствует строгому и систематическому изложению материала и даёт учащимся не только необходимые навыки, но и ясные методологические представления.

Поэтому идеальный урок — тот, на котором учитель направляет, ненавязчиво корректирует работу учащихся, так что у них создается ощущение, что они ведут урок сами.

Несомненно,  что  эмоциональный  компонент  и  мотивация  к  учебной  деятельности  являются  значимыми  критериями  ее  эффективности. Их функция – обеспечение успешности усвоения знаний, умений и навыков на всех этапах развития познавательного интереса к математике как к науке, а именно:

1)                положительным эмоциональным отношением к деятельности, поэтому основой проведения занятий может служить технология деятельностного метода;

2)                наличием познавательной стороны этой эмоции, т.е. радостью познания, которая обеспечивает системное включение ребенка в процесс самостоятельного построения им нового знания и позволяет проводить разноуровневое обучение;

3)                наличие мотива, непосредственно идущего от самой деятельности, используя  интерактивные  методики  (ролевые  игры,  метод проектов,  постановка  эксперимента,  профильные  экскурсии  с «погружением»  в практику тематической области и др.). 

Список литературы

1.     Богуславский  М.В. Абстрактный  гуманизм В.А. Сухомлинского/  М.В.

Богуславский// Свободное воспитание. Вып. 3. – М.: Влади, 1993. – С. 14–17.

2.     Ивашкина Д.А.Эксперимент как метапредметная деятельность: реализация ФГОС на примере курса физики: курс лекций УМП — М.: Педагогический университет «Первое сентября» 2014- 250с

3.     Концепция развития математического образования в Российской Федерации (Утв. Распоряжением Правительства РФ от 24.12.2013 г. № 2506-р). 

4.     Научно-методические рекомендации по формированию эмоционального интеллекта обучающихся  в  образовательной  среде  (основная  школа):  методические рекомендации/  под  общей  и  научной  редакцией  С.В.  Ивановой.  М.:  ФГБНУ  «Институт стратегии развития образования РАО», 2022. 23 с.

5.     Послание Президента Федеральному Собранию Российской Федерации. 1 декабря 2016 г.

6.     Примерная рабочая программа основного общего образования Математика Базовый уровень, Москва 2021г, С.104

7.     Ушинский К. Д. Избранные труды : в 4 кн. / сост., вступ. Ст., примеч. И коммент. Э. Д. Днепрова. Кн. 2. М. : Дрофа, 2005. 

Приложение 1.

Задание «Исторические сведения» Этапы проведения исследования

1.   Формулирование проблемы.

2.   Подготовка к проведению исследования:

- предварительный анализ имеющейся информации, выдвижение гипотез; - отбор материала, который будет использован в исследовании.

3.   Проведение исследования:

- анализ и обобщение результатов исследования.

4.   Изложение результатов исследования, их представление.

5.   Обсуждение, оценка полученных результатов.

Текст.

Дифференциальное исчисление было создано Ньютоном и Лейбницем в конце 17 столетия на основе двух задач:

•              о разыскании касательной к произвольной линии;

•              о разыскании скорости при произвольном законе движения.

Еще раньше понятие производной встречалось в работах итальянского математика Николо Тартальи (около 1500 – 1557гг.) – здесь появилась касательная в ходе изучения вопроса об угле наклона орудия, при котором обеспечивается наибольшая дальность полета снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной.

Посвящает целый трактат о роли производной в математике известный учёный Галилео Галилей. Различные изложения стали встречаться в работах у Декарта, французского математика Роберваля, английского ученого Л.Грегори. Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс.

Мгновенная скорость о разыскании скорости при произвольном законе движения.

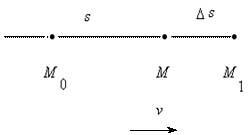
Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M₀ , зависит от времени t , т.е. s есть функция времени t: s = f(t). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M₀, а в некоторый следующий момент t + ∆t оказалась в положении M₁ – на расстоянии s + ∆s от начального положения (см. фото) [3]. Таким образом, за промежуток времени ∆t расстояние s изменилось на величину ∆s. В этом случае говорят, что за промежуток времени ∆t величина s получила приращение ∆s  (изменение «на»).

Отношение  представляет собой среднюю скорость движения точки за время

.

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t. Если, например, тело в начале промежутка ∆t перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t. Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени ∆t. Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при ∆t → 0, как бесконечно малая величина. Этот предел называют скоростью движения в данный момент:

.

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути ∆s к приращению времени ∆t, когда приращение времени стремится к нулю. Так как ∆S = f (t + ∆t) – f(t),

то .

 В жизни, мгновенной скоростью движения автомобиля, является скорость на спидометре в данный момент времени.

Учебные ресурсы  к Приложениям 1-3.

1.     [Электронный ресурс]. Код доступа http://www.cleverstudents.ru

2.     [Электронный ресурс]. Код доступа http://www.krugosvet.ru/images/1012636_image008.gif  

3.     [Электронный ресурс]. Код доступа

http://cdn01.ru/files/users/images/23/2e/232e5e68f95eadc79dee88b42d47f7fe.jpg

4.     Методическое руководство для работы с цифровой лабораторией/ ООО ТД

«Учебное Оборудование L-микро Россия». Москва 2021г.

Приложение 2.

Экспериментальная работа № 4 [4, 15] Измерение магнитной индукции.

Оборудование: датчик напряжения.

Дополнительное оборудование: катушка-моток на платформе, постоянный магнит, компьютер или ноутбук с предустановленным программным обеспечением.

Цель: определить магнитную индукцию катушки при изменении магнитного потока в ней.

Основные сведения. В 1831 г. английский физик Майкл Фарадей установил, что электрический ток в контуре может возникнуть не только при движении проводника в магнитном поле, но и при любом изменении магнитного потока.

Электромагнитная индукция – физическое явление, заключающееся в возникновении электрического тока в замкнутом контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром. Электрический ток, возникающий при электромагнитной индукции, называется индукционным. Направление индукционного тока (так же как и величина ЭДС, в Вольтах) считается положительным, если оно совпадает с выбранным направлением обхода контура, и отрицательным, если оно противоположно этому направлению.

Согласно закону электромагнитной индукции Фарадея–Максвелла:

ЭДС электромагнитной индукции в замкнутом контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром.

ε_i = – Ф^/.

Техника безопасности. Начиная работу, детально ознакомьтесь с заданием и предоставленным оборудованием. Внимательно слушайте и выполняйте все рекомендации педагога. Не используйте приборы без его разрешения.

Порядок проведения работы.

1. Внимательно проанализируйте предоставленные педагогом методические рекомендации. Соберите установку как показано на рисунке.

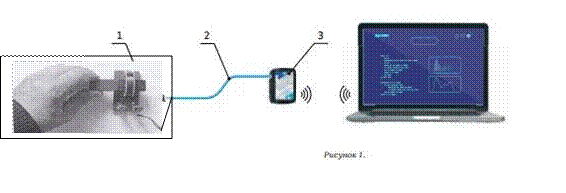
Схема установки:

1     Катушка-моток на платформе с магнитом

2     Соединительные провода

3     Датчик напряжения

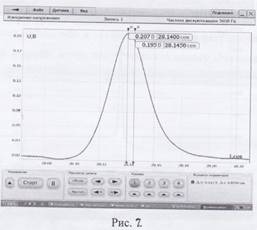
2.     Пример полученного изображения приведен на рис.2.

3.     Таблица результатов.

3.                 Разбейте кривую на 20-30 равных частей. Запишите среднее значение напряжения в каждой части в таблицу.

4.                 Сопротивление катушки 17 Ом. Вычислите значение тока через катушку для каждого выбранного интервала. Запишите в таблицу.

5.                 Количество витков в катушке 250. Вычислите значение заряда, прошедшего через катушку при выдергивании магнита  и значение магнитной индукции B. 

Вопрос.  

Раскройте суть понятия ЭДС электромагнитной индукции, укажите чему равно максимальное значение ЭДС в этом эксперименте.

Приложение   3. 

Учебная карта действий по созданию понятия о производной через анализ и обобщения накопленных данных в ходе теоретического исследования. Методика Ивашкиной Д.А.

15

16

17