
Ф.И.________________________________________________Класс____Дата_______________
Сокращение дробей
|
Правило |
Примеры |
||
|
|
|
|
|
|
1. Разложить числитель и знаменатель на множители: вынести общий множитель за скобки; применить способ группировки слагаемых; применить формулы сокращенного умножения; использовать свойства степеней; другой способ. |
|
ab–bc=b(a–c) a2–2ac+c2=(a–c)2
|
2x+bx–2y–by= =(2x–2y)+(bx–by)= =2(x–y)+b(x–y)= =(x–y)(2+b) 7x–7y=7(x–y)
|
|
2. Зачеркнуть в числителе и знаменателе одинаковые множители в одинаковых степенях. |
|
|
|
|
3. Записать в качестве ответа в числителе и знаменателе не зачеркнутые множители. |
|
|
|
|
Задания: Сократите дробь: |
|||
|
1)
|
|||
|
1)
|
|||
Ф.И.________________________________________________Класс____Дата_______________
Сложение и вычитание дробей
|
Правило |
Примеры |
|
|
|
|
|
|
где P(x), R(x), Q(x) –многочлены и Q(x)¹ 0 |
|
|
|
Задания: Выполните действия: |
||
|
1) |
||
|
1) |
||
Ф.И.________________________________________________Класс____Дата_______________
Умножение дробей
|
Правило |
Примеры |
||
|
|
|
|
|
|
1. Перемножить числитель одной дроби с числителем другой и знаменатель одной дроби со знаменателем другой. |
|
|
|
|
2. Если нужно, сократить получившуюся дробь. |
|
|
|
|
3. Записать ответ. |
|
|
|
|
Задания: Выполните умножение: |
|||
|
1) |
|||
|
|
|||
Деление дробей
|
Правило |
Примеры |
||
|
|
|
|
|
|
1.Представить в виде произведения первой дроби и перевернутой второй дроби. |
|
|
|
|
2. Выполнить умножение получившихся дробей. |
|
|
|
|
3. Записать ответ. |
|
|
|
|
Задания: Выполните деление: |
|||
|
1) |
|||
Ф.И.________________________________________________Класс____Дата_______________
Арифметический квадратный корень
|
Правило |
Примеры |
|
|
|
|
Задания: Найдите значение выражения: |
|
|
1) 6)
|
|
|
1) 6)
|
|
Ф.И.________________________________________________Класс____Дата_______________
Решение неполных квадратных уравнений
|
Правило |
Примеры |
||
|
х2=−9 |
х2=16 |
х2−27=0 |
|
|
Если
а>0, то х= Если а=0, то х=0 Если а<0, то решений нет |
−9<0Þ нет решений |
х= х = ±4 |
х2=27 х=
|
|
Правило |
Примеры |
||
|
Уравнение вида: ах2=0 (a¹0) ах2=0 | : a х2=0 х=0 Ответ: х=0 |
−6х2=0 | :(−6) x2=0 x=0 Ответ: х=0 |
||
|
Уравнение вида: ах2+bx=0 (a¹0) ах2+bx=0 х(ax+b)=0 х=0 или ax+b=0 ax=−b | : a Ответ:
х=0; |
3х2−2х=0 х(3х−2)=0 х=0 или 3х−2=0 3х=2 | :3
х= Ответ: х=0; |
||
|
Уравнение вида: ах2+c=0 (a¹0, c¹0) ах2+c=0 ах2=−c | :a х2= Если
Если
|
2х2+8=0 2х2=-8 | :2 х2=−4 −4<0 Þ нет решений
Ответ: нет решений |
−3х2+27=0 −3х2=−27 | :(−3) х2=9 х=±3
Ответ: х=±3
|
5(х−2)2-45=0 5(х−2)2=45 | :5 (х−2)2=9 x−2=3 x−2=−3 x=5 x= −1
Ответ: х= −1;5 |
1.
![]()
1.
![]()
Ф.И.________________________________________________Класс____Дата_______________
Решение квадратных уравнений по формуле
|
Правило |
Примеры |
|
|
–x(x+7)=(x–2)(x+2) |
х2−6х+9=0 |
|
|
1.
Определить, явл. ли уравнение уравнением вида |
нет |
да |
|
2. Если нужно, раскрыть скобки; привести к общему знаменателю; поделить на число, не равное нулю; привести подобные слагаемые. |
Раскрыть скобки, используя формулу разности квадратов. –x2–7x=x2–4 |
___________ |
|
3.Перенести
все члены получившегося уравнения в левую часть уравнения меняя при этом знак
на противоположный. Привести подобные слагаемые. Т.е. привести уравнение к
виду |
–x2–7x– x2+4=0 –2x2–7x+4=0
|
__________ |
|
4. Выписать коэффициенты уравнения (a, b, c). |
a= –2 b= –7 c=4 |
a=1, b= −6, c=9 |
|
5. Вычислить дискриминант по формуле: D=b2-4ac |
D= b2−4ac=(−7)2−4.(−2).4= =49+32=81 |
D=b2−4ac= =(−6)2−4.1.9= =36−36=0
|
|
6. Если D<0, то решений нет Если
D=0, то Если
D>0, то |
D>0Þ 2 решения
Ответ: x=-4; 0,5 |
D=0Þ Один корень
Ответ: х=3 |
1. х2+3х+2=0 2. х2+4х+4=0 3. 2х2+х+67=0 4. 3х2−24х+45=0 5. 9х2+12х+4=0
Ф.И.________________________________________________Класс____Дата_______________
Площадь прямоугольника, квадрата
|
Формула |
|
||
|
Задание |
Решение |
||
|
Площадь
прямоугольника равна произведению длины и ширины S= a |
Длина прямоугольника равна 28 см, а ширина в 7 раз меньше. Найти площадь прямоугольника. |
1) 28:7=4 см - ширина 2) 4*28=112 см2 - S |
|
|
Длина прямоугольника равна 14 см, а ширина 9 см. Найти площадь прямоугольника. |
14*9=126 см2- S |
||
|
Площадь квадрата равна квадрату его стороны S= a2, где а - сторона квадрата. |
Сторона квадрата равна 6 см. Найти площадь квадрата. |
6*6=62=36 см2 - S |
|
|
Площадь квадрата равна 144 см2. Найти сторону квадрата. |
S=a2 a2=144 a=12 см - сторона 12*12=144 |
||
1. Длина прямоугольника равна 25 см, а ширина в 5 раз меньше. Найти площадь прямоугольника.
2. Длина прямоугольника равна 18 см, а ширина 6 см. Найти площадь прямоугольника.
3. Сторона квадрата равна 8 см. Найти площадь квадрата.
4. Площадь квадрата равна 256 см2. Найти сторону квадрата.
Ф.И.________________________________________________Класс____Дата_______________
Площадь треугольника, параллелограмма
|
Формула |
|
||
|
Задание |
Решение |
||
|
Площадь параллелограмма равна произведению основания на высоту S=
|
Основание параллелограмма равно 10 см, высота 4 см. Найти площадь параллелограмма |
10*4=40 см2 - S |
|
|
Одна из сторон параллелограмма равна 12 см, а опущенная на нее высота равна 10. Найти площадь параллелограмма |
12*10=120 см2- S |
||
|
Площадь треугольника равна половине произведения основания на высоту S= |
Основание треугольника равно 8 см, а высота равна 4 см. Найти площадь треугольника. |
|
|
|
В прямоугольном треугольнике катеты равны 5 см и 4 см. Найти площадь треугольника. |
|
||
1. Основание параллелограмма равно 12 см, высота 6 см. Найти площадь параллелограмма.
2. Одна из сторон параллелограмма равна 15 см, а опущенная на нее высота равна 8. Найти площадь параллелограмма.
3. Основание треугольника равно 14 см, а высота равна 6 см. Найти площадь треугольника.
4. В прямоугольном треугольнике катеты равны 9 см и 8 см. Найти площадь треугольника.
Ф.И.__________________________________________Класс____Дата_______________
Площадь трапеции
|
Формула |
|
||
|
Задание |
Решение |
||
|
Площадь трапеции равна половине суммы оснований на высоту S= |
Основание трапеции равны 7 и 21 см, а высота равна 12 см. Найти площадь трапеции. |
|
|
|
|
Первое основание 4, второе основание 8, высота 3
|
||
|
|||
1. Основание трапеции равны 5 и 21 см, а высота равна 24 см. Найти площадь трапеции.
2. Основание трапеции равны 4 и 32 см, а высота равна 15 см. Найти площадь трапеции.
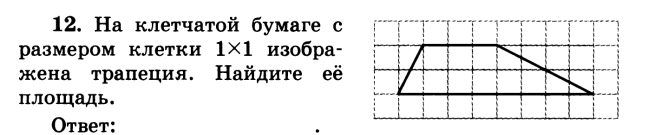
3.
Ф.И.________________________________________________Класс____Дата_______________
Решение линейных уравнений
ПРИМЕР:
2-3(2х+2)=5-4х
Раскрываем скобки:
2-6х-6=5-4х
Переносим неизвестные влево, известные вправо (при переносе меняем знак на противоположный)
-6х+4х=5-2+6
-2х=9
х=9:(-2)
х=-4,5
1) 5-2х=11-7(х+2) 2) 3х+5+(х+5)=1-х+4 3) -х-2+3(х-3)=3(4-х)-3
4). 10(х-9)=7 5). -9(8-9х)=4х+5 6). 1-5х=-6х+8
Ф.И.________________________________________________Класс____Дата_______________
Решение задач по теме:"Параллелограмм"
ПРИМЕР:
1). Диагональ ВД параллелограмма АВСД образует с его сторонами углы равные 65 и 50 градусов. Найдите меньший угол параллелограмма.
Решение: Угол В и угол Д - это тупые углы параллелограмма, найдем их
угол В=65+50=115 градусов. Сумма углов в параллелограмме 360 градусов. Найдем острые углы
угол А и угол С = 360-(115+115)=360-230=130 градусов; 130:2=65 градусов угол А.
Ответ 65.
2). Один угол параллелограмма в 2 раза больше другого. Найдите меньший угол.
Решение: Пусть х - первый угол параллелограмма, второй угол 2х. Составим уравнение:
х+х+2х+2х=360
6х=360
х=60 градусов (меньший угол параллелограмма)
№ 1. Диагональ АС параллелограмма АВСД образует с его сторонами углы, равные 30 и 45 градусов. Найдите больший угол параллелограмма.
№ 2. Диагональ ВД параллелограмма АВСД образует с его сторонами углы равные 50 и 85 градусов. Найдите меньший угол параллелограмма.
№ 3. Диагональ АС параллелограмма АВСД образует с его сторонами углы, равные 30 и 35 градусов. Найдите больший угол параллелограмма.
№ 4. Один угол параллелограмма в 4 раза больше другого. Найдите меньший угол.
Ф.И.________________________________________________Класс____Дата_______________
Решение задач по теме:"Трапеция"
ПРИМЕР:
1. Найдите больший угол равнобедренной трапеции АВСД, если диагональ АС образует с основанием АД и боковой стороной АВ углы, равные 30 и 45 градусов.
Решение: Углы А и С - острые, углы В и Д - тупые. Найдем острый угол А=30+45=75 градусов.
Сумма острых углов равна 75+75=150 градусов.
Найдем тупые углы (360-150):2=210:2=105 градусов.
Ответ 105 градусов.
2. Сумма двух углов равнобедренной трапеции равна 140 градусов. Найдите больший угол трапеции.
Решение: (360-140):2=220:2=110 градусов больший угол.
№ 1. Найдите больший угол равнобедренной трапеции АВСД, если диагональ АС образует с основанием АД и боковой стороной АВ углы, равные 40 и 55 градусов.
№ 2. Сумма двух углов равнобедренной трапеции равна 220 градусов. Найдите меньший угол трапеции.
№ 3. Найдите больший угол равнобедренной трапеции АВСД, если диагональ АС образует с основанием АД и боковой стороной АВ углы, равные 25 и 40 градусов.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.