Кейс «Применение подобия для решения практических задач»

Кейс «Применение подобия для решения практических задач»

Вид кейса: печатный

Тип кейса: практический.

Содержание кейса: В современном мире мы определяем значения различных величин (длину, массу, температуру и т. п.) с помощью различных инструментов и приборов. Так, в своей профессиональной деятельности строители, архитекторы, лесоводы, военные для определения высоты объекта используют специальные сложные и дорогостоящие приборы – высотомеры. Можем ли мы определить высоту здания или дерева без использования технических средств, полагаясь только на то, что есть «под руками»?  Помочь нам в этом может геометрия. Геометрия – это не просто наука о свойствах геометрических фигур. Геометрия – это целый мир, который окружает нас с самого рождения. Вам порою кажется, что геометрия совершенно не связана с нашей жизнью, что это очень трудная и совсем непонятная наука. Вам предоставляется шанс по-новому взглянуть на этот предмет. Желаю всем успешной работы.

Теория

С древних времен строители имели дело с  пропорциями. Правильные соотношения, возводимых ими дворцов и храмов придавало этим зданиям ту необыкновенную красоту, которая восхищает нас и сегодня. Древнегреческие математики очень искусно преобразовывали пропорции, доказывали с их помощью самые сложные утверждения, решали самые сложные задачи.

1.     Говорят, что отрезки AB и СD пропорциональны отрезкам A₁B₁ и C₁D₁, если  .

2.     Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Коэффициентом подобия называется число k, равное отношению сходственных сторон.

3.     Признаки подобия треугольников:

I.                   Два треугольника подобны, если два угла одного треугольника соответственно равны  двум углам другого треугольника.

II.                Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

III.             Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.

4.     Измерительные инструменты, используемые при измерении на местности:

Рулетка – лента, с нанесёнными на ней делениями, предназначена для измерения расстояния на местности.

Экер – прибор для построения прямых углов на местности.

Астролябия – прибор для измерения углов на местности.

Вехи (вешки) – колья, которые вбивают в землю.

1. Построение прямой на местности (провешивание прямой линии)

Отрезки на местности обозначают с помощью вех. Чтобы вешка стояла прямо, применяют отвес (какой – либо грузик, подвешенный на нитке). Ряд вбитых в землю вех и обозначает отрезок прямой линии на местности. В выбранном направлении ставят две вехи на расстоянии друг от друга, между ними другие вехи, так, чтобы глядя через одну, другие прикрывались друг другом.

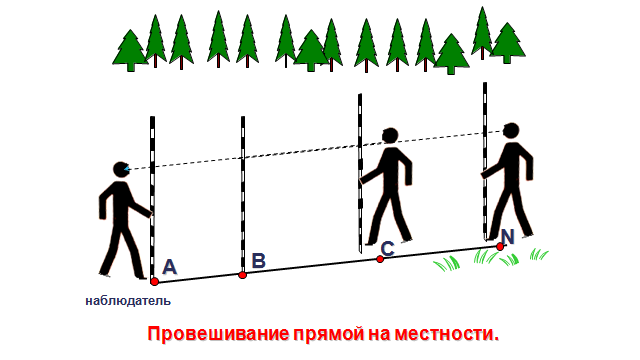
2. Измерение средней длины шага.

Считается некоторое число шагов (например, 50), измеряется данное расстояние и вычисляется средняя длина шага. Опыт удобнее провести несколько раз и сосчитать среднее арифметическое.

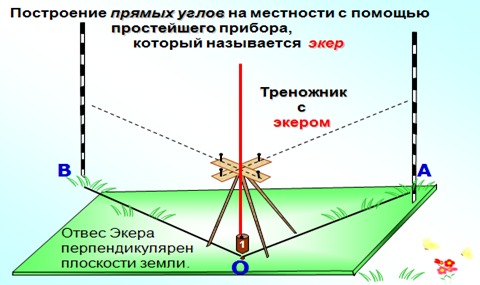
3. Построение прямых углов на местности.

Чтобы построить на местности прямой угол АОВ с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (ОВ).

4. Построение и измерение углов с помощью астролябии.

Астролябию устанавливают в вершине измерительного угла так, чтобы лимб её был расположен в горизонтальной плоскости, а отвес, подвешенный под центром лимба, проектировался бы в точку, принимаемую за вершину угла на поверхности земли. Затем визируют алидадой по направлению одной стороны измеряемого угла и отсчитывают на лимбе градусные деления против метки предметного диоптра. Повёртывают алидаду по ходу часовой стрелки в направлении второй стороны угла и делают второй отсчёт. Искомый угол равен разности показаний при втором и первом отсчётах.

План работы группы:

1.   Определите организатора, перед которым будет стоять задача руководить работой группы.

2.   Определите секретаря, который будет фиксировать предложенные решения ситуаций.

3.   Внимательно изучите материалы кейса

4.   Обсудите изученную информацию, вспомните необходимые теоретические сведения.

5.   Обменяйтесь мнениями и составить план работы над задачей (ситуацией).

6.   Проанализируйте материал.

7.   Определите сущность ситуации.

8.   Зафиксируйте основные и второстепенные проблемы.

9.   Работайте над проблемой (дискуссия).

10. Выработайте решение задачи.

Требуется: определить   высоту объекта (столба, здания школы, и т.д);

а)     Объясните, используя признаки подобия треугольников данный способ определения высоты.

б)    Определите преимущества и недостатки такого способа определения высоты предмета.

11. Подготовьте  проект (оформить).

12. Решите задачи

Ситуация: По некоторым преданиям 21 июля 1798 г. генерал Бонапарт произнес перед сражением при египетских пирамидах такие красивые слова: «Сорок веков смотрят на вас с высоты этих пирамид». А как определить высоту такого огромного сооружения?

Притча

   « Усталый чужеземец пришёл  в страну Великого Хапи. Солнце уже садилось, когда он подошёл к великолепному дворцу фараона. Он что-то сказал слугам. По мгновению распахнули перед ним двери и провели его в приёмную залу. И вот он стоит в запылённом походном плаще, а перед ним на золоченом троне сидит фараон. Рядом стоят высокомерные жрецы, хранители великих тайн природы.  

- Кто ты? – спросил верховный жрец.   

-Зовут меня Фалес. Родом я из Милета.

Жрец надменно продолжал:

-Так это ты похвалялся, что сможешь измерить высоту предмета, не взбираясь на неё? – Жрецы согнулись от хохота. – Будет хорошо, - насмешливо продолжал жрец, - если ты ошибёшься не более чем на 100 локтей.

- Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.

  Лица жрецов потемнели. Какая наглость! Этот чужеземец утверждает, что может вычислить то, чего не могут они – жрецы великого Египта.

Хорошо, - сказал фараон. – Около дворца стоит пирамида, мы знаем её высоту. Завтра проверим твоё искусство».

На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту. Что сказал Фалес?

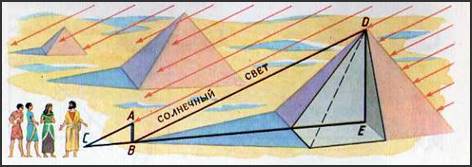
Слова Фалеса: Когда тень от палки стала  той же длины, что и сама палка, то длина тени от центра основания пирамиды до её вершины  имеет ту же длину, что и сама пирамида.

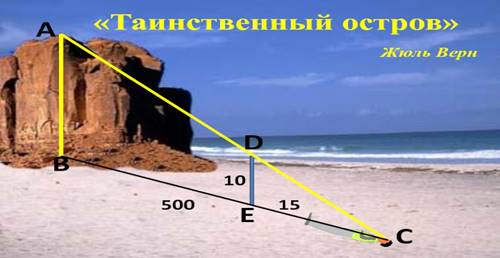
2 Ситуация: отрывок из романа Ж. Верна «Таинственный остров»

В книге повествуется о событиях, происходящих на необитаемом острове в Южном полушарии. Основными персонажами являются пятеро американцев, которые волею судьбы оказались на нем. Для определения координат острова им нужно измерить высоту над уровнем моря плато Дальнего вида, расположенного на этом острове.

«-Сегодня нам надо измерить высоту площадки Дальней скалы, - сказал инженер.

Вам понадобится для этого инструмент? – спросил Герберт.

Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

 Взяв прямой шест, длиной 12 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком. Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.

 «Тебе знакомы зачатки геометрии? – спросил он Герберта, поднимаясь с земли.

-Да.

-Помнишь свойства подобных треугольников?

-Их сходственные стороны пропорциональны.

-Правильно. Так вот: сейчас я построю 2 подобных прямоугольных треугольника. У меньшего одним катетом, будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника. - Понял! – воскликнул юноша. – Расстояние от колышка до шеста так относится к расстоянию от колышка до основания стены, как высота шеста к высоте стены.

- Да. И следовательно, если мы измерим два первых расстояния, то зная высоту шеста, сможем вычислить четвёртый, неизвестный член пропорции, то есть высоту стены. - Оба горизонтальных расстояния были измерены: меньшее равнялось 15 футам, большее – 500 футам. По окончании измерений инженер составил следующую запись: 15 : 500 = 10 : х, 500 × 10 = 5000, 5000 : 15 = 333,8. Значит, высота гранитной стены равнялась 333 футам» (1 англ. фут-30 см)

3   

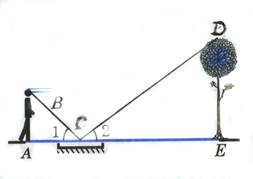
Ситуация:  Однажды сын проходил с отцом по двору. Недавно прошёл дождь, и во дворе было много небольших луж. Посреди двора росло большое дерево. Сын спросил отца: «Чему равна высота этого дерева?» На этот вопрос отец ответил: «Давай не будем гадать, а измерим его высоту …   с помощью лужи. Я знаю свой рост – 180 см. Мне надо знать, на какой высоте расположены глаза. Думаю, мы не сильно ошибемся, если будем считать это расстояние равным 170 см. Мой шаг равен 90 см… А впрочем, это не важно. Сейчас я встану так, чтобы я мог видеть в этой луже отражение вершины дерева. Теперь подсчитаем, сколько шагов от меня до лужи. Получилось 3 шага. Так, а чему равно расстояние от лужи до дерева?.. 30 шагов. Значит, высота дерева равна…»

       Чему равна высота дерева?

Задачи для решения:

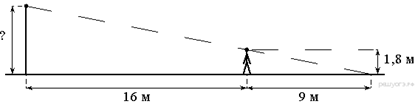1. Че­ло­век, рост ко­то­ро­го равен 1,8 м, стоит на рас­сто­я­нии 16 м от улич­но­го фо­на­ря. При этом длина тени че­ло­ве­ка равна 9 м. Опре­де­ли­те вы­со­ту фо­на­ря (в мет­рах).

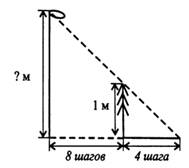2. Дерево высотой 1 м находится на расстоянии 8 шагов от фонарного столба и отбрасывает тень длиной 4 шага. Определите высоту фонарного столба

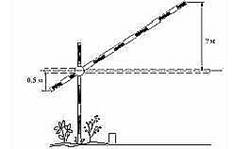3.  Короткое плечо шлагбаума имеет длину 1м, а длинное плечо 4м. На какую высоту (в метрах) поднимается конец длинного плеча, когда конец короткого опускается на 0,5м?

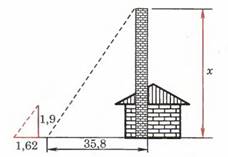
4        . Длина тени фабричной трубы равна 35,8 м; в это же время вертикально воткнутый в землю кол высотой 1,9 м дает тень длиной 1,62 м. Найдите высоту трубы.  

5. В деревне у бабушки растёт старый тополь, который Вам необходимо спилить. В 10 м от тополя стоит забор. Определите, упадёт ли тополь на забор, если в 8 м от дерева находится лужа, отойдя от которой на 1,5 м вы видите верхушку тополя (рост человека 1м 70 см).

Лист самооценки

Поставь:

 1- я знаю и умею, но нужна помощь

2- я использую в стандартных ситуациях

3- я уверенно применяю в любых ситуациях

 Литература и ресурсы интернет:

1.     Геометрия 7-9. Учеб. Для общеобразоват. учреждений/ Л.С.Атанасян , В. Ф. Бутузов ,С. Б. Кадомцев. М.: Просвещение,  2015

2.     Ж. Верн Собрание сочинений: в 20 т. Т.9: Таинственный остров: Роман: Ч. 1,2 .-М.: Терра, 1997.

3.     Притча о Фалесе  https://www.litmir.me/br/?b=149642&p=33

4.     http://festival.1september.ru/articles/418615/

5.     Задачи:  https://oge.sdamgia.ru

6.     Скачано с www.znanio.ru