Кинематика (1)

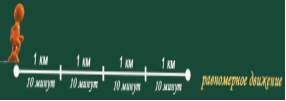
Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:       v_cp = v

Скорость равномерного прямолинейного движения – это физическая векторная величина, равная отношению перемещения тела  за любой промежуток времени к значению этого промежутка t:                  =  / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:   =  • t

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

v_x = v,   то есть v > 0

Проекция перемещения на ось ОХ равна:   s = vt = x – x₀

где x₀ – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения, то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x₀ + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид: х = x₀ - vt

Зависимость скорости, координат и пути от времени

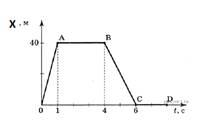
Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

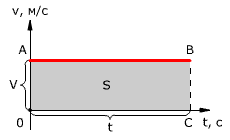
График зависимости перемещения от времени показан на рис. 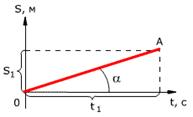 Из графика видно, что проекция скорости равна

v = s₁ / t₁ = tg α,         где α – угол наклона графика к оси времени.

Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

tg α = v

Зависимость координаты от времени показана на рис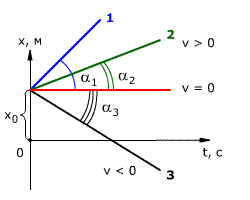Из рисунка видно, что

tg α₁ > tg α₂

следовательно, скорость тела 1 выше скорости тела 2 (v₁ > v₂).

tg α₃ = v₃ < 0

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

х = х₀

ü  Чтение графиков движения

ü  Построение графиков движения

ü  Нахождение скорости по графику движения

Система отсчета

Графическое представление движения очень часто помогает наглядности и пониманию того, как движется тело. На графике удобно показывать, как можно выразить ту или иную величину. Обратите внимание, что для изображения движения необходимо правильно выбрать систему отсчета. Поскольку мы рассматриваем равномерное прямолинейное движение, то за ось абсцисс принимаем ось времени, ось ординат определяет координату тела (см. рис. 1).

График движения тела вдоль прямой с положительной скоростью

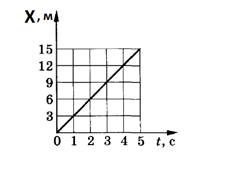
Рассмотрим график движения тела вдоль прямой с положительной скоростью. На рис. 2 представлено две линии. Одна линия (голубого цвета) соответствует движению тела из начала координат . Уравнение этого графика можно записать в виде:  – линейная зависимость координаты от времени. Скорость в данном случае положительна.

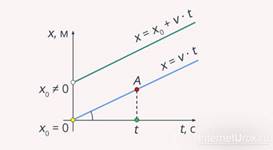
Выше первого графика располагается график (зеленого цвета), который соответствует случаю, когда тело начинает свое движение уже не из начала координат, а из какой-либо точки . Данная линия может быть записана в виде: . Тело также будет двигаться пропорционально времени, но в этом случае существует ненулевая начальная координата тела.

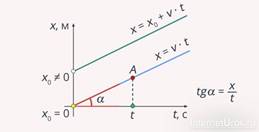
Обратите внимание, что угол  характеризует скорость движения (см. рис. 3). Катет  соответствует изменению координаты . Второй катет соответствует расстоянию от  до точки . Тогда, записав определение тангенса угла, получим:

Чем больше угол наклона, тем, соответственно, больше скорость движения тела.

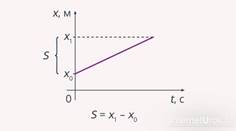
График движения тела позволяет определить модуль перемещения  (см. рис. 4). Между тем, по графику можно также определить пройденный телом путь: при равномерном движении он равен модулю перемещения тела.

График движения тела вдоль прямой с отрицательной скоростью

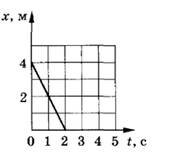
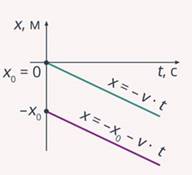
Рассмотрев рис. 5, можем утверждать, что тело двигалось с отрицательной скоростью. Одна линия соответствует движению тела против оси Ох и выходит из начала координат . В данном случае уравнение движения будет иметь вид: . Вторая линия характеризует движение тела не из начала координат, а из какой-то точки . Уравнение движения будет иметь вид: .

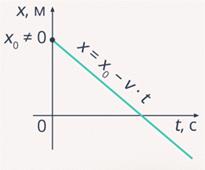
Рассмотрим график на рис. 6. В данном случае тело начинает свое движение из точки, которая находится выше начала координат , однако скорость при этом остается отрицательной. Уравнение движения тела будет иметь вид: .

Рассмотрим еще один график движения тела (см. рис. 7).С течением времени, до значения времени , координата тела не меняется,  и только от красной точки график начинает подниматься вверх. Это означает, что за время, равное  тело находилось в состоянии покоя. Его координата в данной системе отсчета не изменялась. И только из точки, обозначенной на рисунке красным цветом, тело начинает двигаться, то есть появляется у тела скорость.

График зависимости скорости движения тела от времени

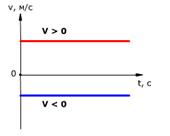
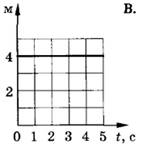
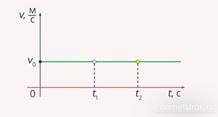
На рис. 8 приведен пример графика в системе отсчета с осью абсцисс – осью времени – и осью ординат – осью скорости. Для равномерного прямолинейного движения скорость остается величиной постоянной. Поэтому график скорости такого движения – прямая линия, параллельная оси времени.

           Геометрический смысл пройденного пути

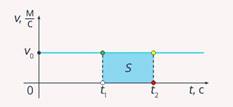
В заключение урока отметим тот факт, что при помощи графиков очень удобно изобразить и определить пройденный телом путь. Дело в том, что геометрическое толкование пройденного пути – это площадь фигуры, ограниченной с одной стороны осью времени, а с другой стороны – графиком скорости.

Рассмотрим график скорости (см. рис. 9) для равномерного движения – прямая, параллельная оси времени. Возьмем отрезок времени от  до , тогда площадь фигуры  – пройденный телом путь.

1.                Задачи 21, 22, 24, 27 – сб. задач А.П. Рымкевич, изд. 10.

2.                Парашютист спускается со скоростью 18 км/ч. На высоте 1000 метров из его кармана падает шарик от настольного тенниса и летит равномерно со скоростью 54 км/ч. Определите графически, какое время пройдет между приземлением шарика и парашютиста

Скачано с www.znanio.ru