ГОСУДАРСТВЕННОЕ  КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ  РОСТОВСКОЙ ОБЛАСТИ

«РОСТОВСКАЯ-НА-ДОНУ САНАТОРНАЯ  ШКОЛА-ИНТЕРНАТ  №  74»

Открытый урок по математике в 3 классе

Тема: «Решение  топологических  задач»

Воспитатель: Кошуба Нина Николаевна

Цель: Развитие топологических представлений младших школьников(знакомство с понятием внутренняя область, граница объекта, внешняя граница).  Расширять  кругозор  учащихся.

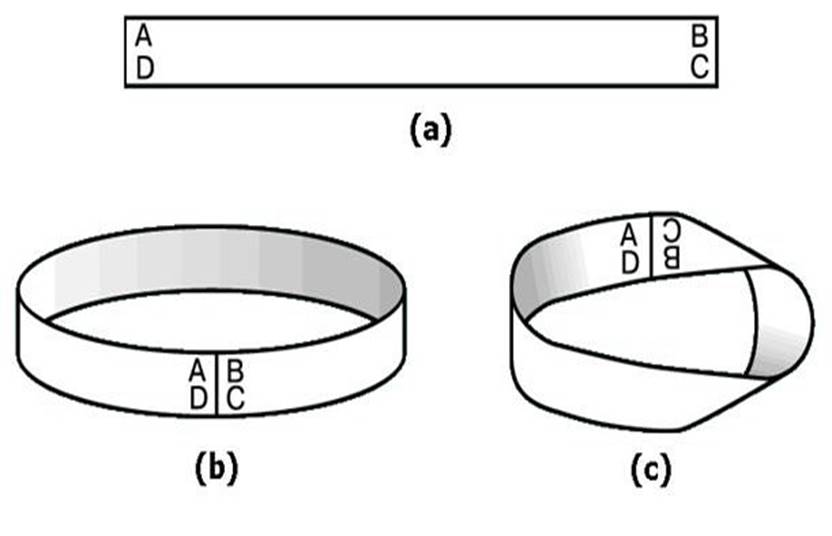
u   У первой полоски склеим её противоположные концы.

u   У второй полоски тоже склеим её противоположные концы, но при этом предварительно перевернём один из них.

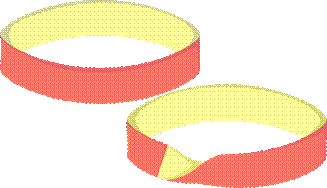
u   Эти кольца очень похожи.

u   Но представьте муравья, находящегося на поверхности простого кольца. Удастся ли ему попасть на обратную (изнаночную) сторону кольца, не переползая через край ленты?

u   Конечно же, не получится!

u   А если муравей будет ползти по перекрученному кольцу?

u   Давайте проведём непрерывную линию по одной из сторон перекрученного кольца. Линия прошла по обеим сторонам кольца, хотя она была проведена непрерывно.

u   Это и обнаружил Мёбиус.

Односторонняя поверхность – лист Мёбиуса – положила начало целому направлению в геометрии. Но по-прежнему привлекает к себе внимание не только учёных, но и людей творческих профессий. Международный символ переработки отходов представляет собой лист Мёбиуса.

Продолжим  рассматривать  опыты с   листом Мёбиуса и подобными ему кольцами.

Возьмём простое кольцо и перекрученное на полоборота кольцо (лист Мёбиуса). Разрежем вдоль каждое из них. Разрезав обычное кольцо, у нас получилось два кольца.

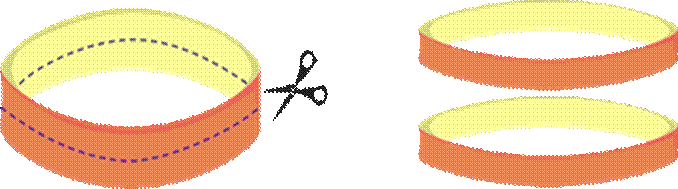
При этом длина окружности каждого кольца та же, но кольца в два раза уже.

Разрезав лист Мёбиуса, мы получили кольцо, которое перекручено на два полуоборота,

длина его окружности в два раза больше, и кольцо уже исходного в два раза. Хотя казалось бы, что лист должен был распасться.

А вот если взять ленту Мёбиуса шириной 3 см и разрезать её вдоль, отступив от края на 1 см, то получим два кольца – одно большое и сцепленное с ним маленькое. При этом маленькое кольцо – это лента Мёбиуса. Большое представляет собой кольцо, которое перекручено на два полуоборота.

Домашнее задание