Федеральное государственное автономное образовательное учреждение

высшего образования

«Дальневосточный федеральный университет»

 

 

 

Студент гр. Б9119-09.03.02 Тумасова Я. А.

 

Комплекс лабораторных работ по вычислительным методам

Часть 1

 

 

 

 

 

 

 

 

 

 

 

Владивосток

2023

Оглавление

Пояснительная записка. 3

Требование к оформлению отчетности по лабораторным работам.. 4

I. Тема: Численные методы решения нелинейных уравнений. 5

II. Тема: Интерполяционные численные методы.. 15

III. Тема: Численное интегрирование. 21

IV. Тема: Одномерная оптимизация. 31

V. Тема: Многомерная оптимизация. 37

 

 

Пояснительная записка

Данный комплекс лабораторных работ создан для освоения базовых знаний по вычислительным методам и овладения навыками их программирования. Вычислительные методы (численные методы) – это методы вычислительной математики, преобразующие решение математических задач в алгоритмы с числами и арифметическими действиями, для решения на ЭВМ.

Комплекс в большей части направлен на ознакомление с алгоритмами численных методов, которые применяются как в решении других более сложных численных методов, так и в прикладных задачах (автоматизирование расчётов в системах, машинное обучение, калькуляторы).

Лабораторные работы имеют низкий входной порог по знаниям математики: нет сложных и громоздких выводов формул, для каждого метода представлен свой алгоритм. Все данные объясняются на языке, понятном для человека, который не проходил углубленный курс высшей математики, или проходил только основы высшей математики.

Комплекс рекомендован для:

1. Студентов средних специальных учебных заведений, проходящих обучение на IT-специальности;

2. Студентов младших курсов высшего учебного заведения, проходящих обучение на IT-специальности;

3. Людей, которые хотят ознакомиться и освоить численные методы.

Для выполнения лабораторных работ рекомендуется использовать среду разработки Microsoft Visual Studio для продвинутых пользователей и операционных систем: Windows, MacOS, Linux. Для начинающих рекомендована среда разработки Dev-C++ для операционной системы Windows.

Требование к оформлению отчетности по лабораторным работам

Отчетность состоит из:

1. Отчет в .docx файле;

2. Программа с выполненной лабораторной работой.

Отчет должен включать:

1. титульный лист (название дисциплины и раздела, тема, ФИО студента, направление подготовки, группа);

2. цель выполненной лабораторной работы;

3. основную часть (текст программы (фото экрана с кодом программы), фото экрана с выводом ответа программы, описание работы программы);

4. выводы (анализ и обоснование результатов выполнения работы);

5. ответы на контрольные вопросы.

Отчет должен быть оформлен по ГОСТ 7.32― 2017 «Отчет о научно-исследовательской работе. Структура и правила оформления».  Формат отчета:

1. Размер шрифта отчета 14;

2. Шрифт «Times New Roman»;

3. Выравнивание «по ширине»;

4. Нумерация страниц в правом нижнем углу (на первой странице особый колонтитул для первой страницы).

               I. Тема: Численные методы решения нелинейных уравнений

Цель: изучить методы решения нелинейных уравнений и овладеть практическими навыками их решения на языке программирования.

Теоретическая часть:

Пусть дано уравнение

                                                    (1.1)

где  – нелинейная функция. Решить уравнение (1.1), значит найти совокупность значений , подстановка которой в уравнение (1.1), обращает данное уравнение (1.1) в верное числовое равенство.

Численные методы предполагают два этапа решения нелинейных уравнений:

1. Отделение корней нелинейного уравнения;

2. Вычисление приближенных значений корней с точностью .

Первый этап содержит в себе предварительный анализ уравнения с целью определения количества и примерного местонахождения корней. Требуется найти отрезки, каждый из которых содержит ровно один корень. Существует два метода отделения корней:

1. Графический;

2. Аналитический (табличный).

Данные методы можно реализовать как ручным расчетом, так и расчетом в MS Excel.

Графический метод отделения корней нелинейного уравнения состоит в построении графика функции  На пересечении графика функции с осью абсцисс будет находиться приближенное значение корня уравнения. Следовательно, из данного графика можно взять примерный отрезок, в котором находится корень данного уравнения.

Если функция  имеет сложный вид, то ее следует представить в виде разности двух функций , при этом выполняется неравенство , так как . При построении графиков функций  и  абсциссы точек пересечения этих графиков будут являться приближёнными значениями корней.

Пусть нелинейное уравнение имеет вид  , тогда  и . Графики данных функций представлены на рис. 1, из которого видно, что исходное уравнение имеет 3 корня, которые находятся на отрезках [-1, -0.75], [-0.25, 0], [0.75, 1].

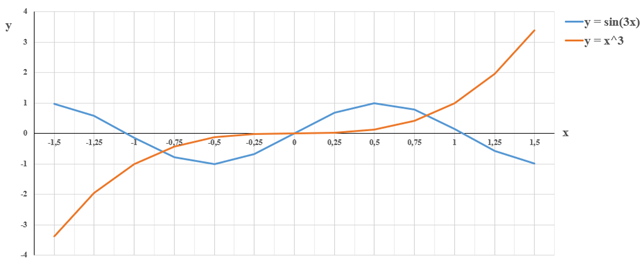
Рисунок 1 - Графики функций

Аналитический (табличный) метод предполагает, что если функция  непрерывна на отрезке [a, b], а на концах отрезка её значения имеют разные знаки, т. е , то на этом отрезке расположен, по крайней мере, один корень.

 

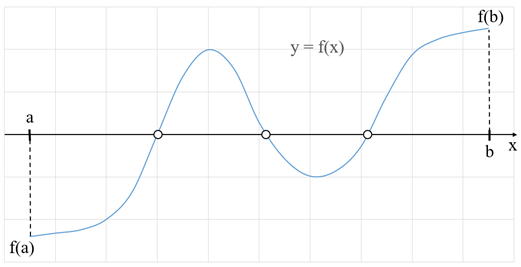
Рисунок 2 - Аналитический (табличный) метод

Рассмотрим пример на уравнении из графического метода.

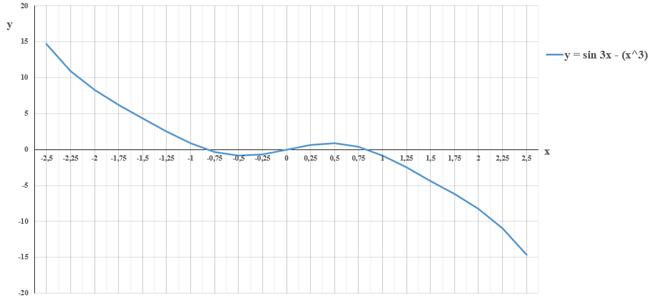
Рисунок 3 - График функции

Таблица 1 - Аналитический (табличный) метод

 

Из табличных данных, по которой строился график видно, что знак корня функции меняется три раза, значит у функции существуют корни на отрезках [-1, -0.75], [-0.25, 0], [0.75, 1].

Вычисление приближенных значений корней с точностью  выполняется с помощью численных методов. Существует большое количество методов решения нелинейных уравнений. В данной лабораторной работе будут описаны метод деления отрезка пополам и метод касательных (Ньютона).

1. Метод деления отрезка пополам

Дано уравнение (1.1), [a, b] – отрезок с корнем и  – точность. Найдем середину отрезка:

 .                                              (1.2)

С помощью данной формулы (1.2) отрезок делится пополам, половина, не содержащая корень, отбрасывается, другая половина делится пополам при помощи формулы (1.2), и цикл повторяется. Когда отрезок станет меньше точности – любую его точку можно взять в качестве ответа. На рисунке ниже (рис. 4) представлено графическое изображение метода, где  – итерация деления отрезка.

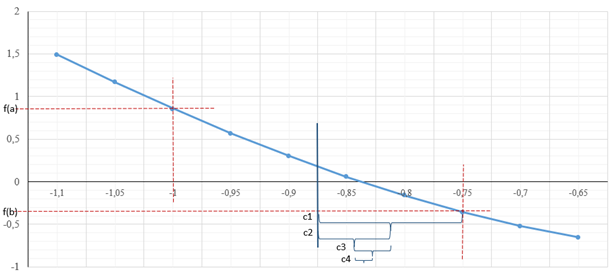
Рисунок 4 - Графическое изображение деления отрезка пополам

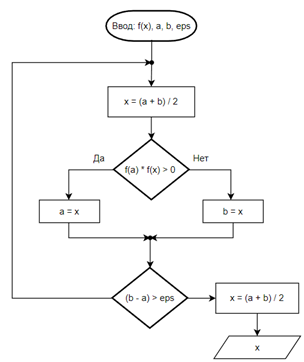
Рисунок 5 - Алгоритм метода деления отрезка пополам

Достоинства метода:

1) Прост в реализации;

2) Надежный – метод работает при любой непрерывной функции;

3)  Устойчивый к ошибкам округления – можно найти корень с любой точностью увеличивая количество итераций.

Недостатки метода:           

1) Низкая скорость работы метода;

2) Если отрезок [a, b] был определен не верно и содержит более одного корня, то все корни кроме одного потеряются.

2. Метод касательных (Ньютона)

Дано уравнение (1.1), [a, b] – отрезок с корнем и  – точность. Необходимо найти производную уравнения (1.1)  и начальное приближение , которое, обычно, является одним из концов отрезка [a, b]. Начальное приближение должно удовлетворять следующему условию:

где  – значение одного из концов отрезка [a, b].

 Далее необходимо воспользоваться алгоритмом (рис. 6), где используются вышеперечисленные входные данные и модифицированное уравнение касательной, проведенной к кривой :

где . Это уравнение (1.3) используется для нахождения точки пересечения касательной с осью , то есть для нахождения приближения корня . Значение уравнения (1.3)  находится в цикле. Условия окончания цикла нахождения приближений написано в алгоритме метода касательных (рис. 6).

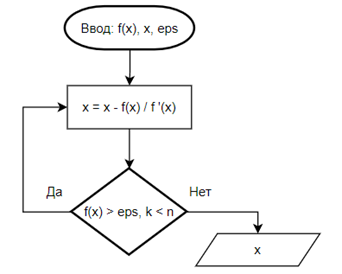
Рисунок 6 - Алгоритм метода касательных (Ньютона)

Достоинства метода:

1) Очень быстрая сходимость.

Недостатки метода:           

1) Необходимо находить производную на каждой итерации;

2) Не применим к недифференцируемым функциям;

3) Процесс нахождения приближения корня может расходиться, если начальное приближение далеко от корня.

Практическое задание:

1) Определите начальное приближение аналитическим или графическим способом, представьте его в отчете.

2) Напишите программу, для реализации уточнения корней нелинейного уравнения методом деления отрезка пополам и методом касательных (Ньютона) на языке C++. Каждый метод должен выводить все найденные корни и количество итераций, понадобившихся для нахождения каждого корня. Количество итераций цикла в методе касательных (Ньютона) не должно превышать 1000. Оформлять методы лучше в функции.

3) Ответьте на контрольные вопросы.

4) Оформите отчет, и отправьте его и программу на почту преподавателю.

Примерное время выполнения задания – 4,5 часа.

Нелинейное уравнение необходимо взять из списка, приведенного ниже. Номер варианта должен соответствовать порядковому номеру в списке группы.

Контрольные вопросы:                 

1) Опишите сущность метода деления отрезка пополам.

2) Когда метод деления отрезка пополам надежный?

3) В каких случаях применение метода Ньютона не рекомендуется?

4) Что будет, если взять приближение в методе Ньютона достаточно далеко от корня?

Перечень вспомогательной литературы:

1. Метод касательных // mathprofi.ru URL: http://mathprofi.ru/metod_kasatelnyh.html (дата обращения: 05.05.2023);

2. Маркин П. М., Основы математического аппарата инженера-системотехника вычислительной техники. Учебное пособие для студентов специальности 2201 (Вычислительные машины, комплексы, системы и сети): учебное пособие – Москва: 2006;

3. Зенков, А. В., Численные методы: учеб. пособие — Екатеринбург: Изд-во Урал. ун-та, 2016.— 124 с.

 

 

            II. Тема: Интерполяционные численные методы

Цель: изучить интерполяционный численный метод и овладеть практическими навыками нахождения неизвестных промежуточных значений функции на языке программирования.

Теоретическая часть

Интерполяция – это способ приближенного или точного нахождения неизвестных промежуточных значений функции, по имеющемуся дискретному набору её известных значений. На практике интерполяцию применяют, когда необходимо найти промежуточное значение функции, заданной таблично: в точках  известны значения функции .

Задача интерполирования заключается в нахождении функции , которая обычно является алгебраическим многочленом, и проще интерполируемой функции , и в заданных точках будет совпадать с известными значениями функции , т.е.

.

В остальных точках отрезка  значения функции  приближенно описывает интерполируемую функцию .

В геометрическом понимании интерполирование является построением кривой , проходящей через заданные таблично точки. Ниже, представлен график (рис. 1), на котором изображена интерполируемая функция, заданная таблично и интерполирующая функция , т.е.

.

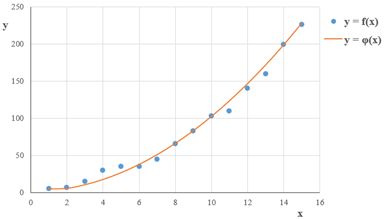
Рисунок 7 - Геометрическое изображение интерполирования

Нахождение неизвестных промежуточных значений функции выполняется с помощью численных методов, при этом погрешность вычисления этих значений невозможно оценить, так как существует бесконечное множество функций, проходящих через заданные точки.

Существует большое количество методов нахождения интерполирующей функции. В данной лабораторной работе будет описан метод Лагранжа.

Метод Лагранжа

В данном методе используется интерполяционный полином Лагранжа:

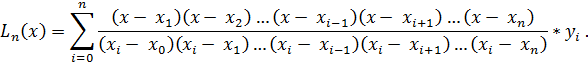
Данный полином можно также записать в виде:

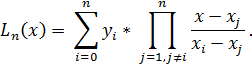
Степень интерполяционного полинома Лагранжа зависит от числа узлов, которые берутся для его построения:

1) Если берется 2 ближайших известных узла функции для построения полинома, то , и это линейное интерполирование;

2) Если берется 3 ближайших известных узла функции для построения полинома, то , и это квадратичное интерполирование;

3) Если берется 4 ближайших известных узла функции для построения полинома, то , и это кубическое интерполирование.

Пример:

Для функции  построить интерполяционный кубический полином Лагранжа, по узлам из таблицы, приведенной ниже, и найти корень в точке .

Таблица 2 - Корни и значения функции

Построим кубический полином Лагранжа по таблице 2:

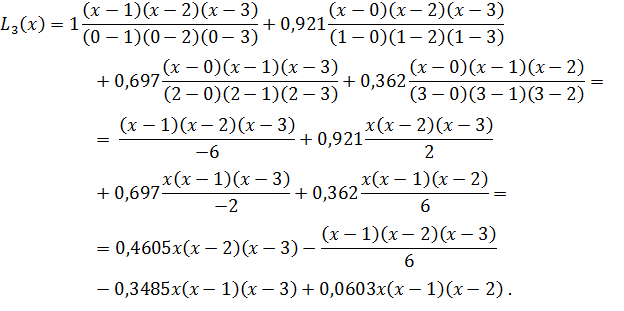
Теперь подставим в получившийся полином , для нахождения корня в данном узле:

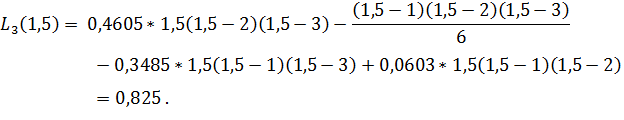
При расчете на калькуляторе, при значении корень  , значения схожи – решение было проведено верно.

При написании программы должно быть три цикла:

1)    На сложение;

2)    На деление;

3)    На произведение.

Достоинства:

1) Простая для понимания интерполяционная формула;

2) Можно строить полином не по всем точкам, а по нескольким, ближайшим к нужной;

3) Интервалы между узлами  могут быть неравномерными.

Недостатки:

1) При изменении степени полинома все расчёты нужно проделывать заново.

Практическое задание:

1) Напишите программу для нахождения значений таблично заданной функции с использованием кубического интерполирования метода Лагранжа. Узлы интерполирования должны находиться в средних точках между значениями функции.

2) Ответьте на контрольные вопросы.

3) Оформите отчет по требованиям, и отправьте его и программу на почту преподавателю.

Примерное время выполнения задания – 6 часов.

Табличные значения функции необходимо взять из списка, приведенного ниже. Номер варианта должен соответствовать порядковому номеру в списке группы.

№ варианта	Значения аргументов и функций
1	y	1	2	3	4	5	6	7
	x	0	0,4	1,2	2,4	4	6	8,4
2	y	1	2	3	4	5	6	7
	x	0	0,102	0,378	0,972	2,1	4,05	7,182
3	y	1	2	3	4	5	6	7
	x	1,3125	3,25	5,8125	9	12,8125	17,25	22,3125
4	y	1	2	3	4	5	6	7
	x	5	15,5	23	29,75	36,2	42,5	48,71429
5	y	1	2	3	4	5	6	7
	x	0,2	1,6	5,4	12,8	25	43,2	68,6
6	y	2	3	4	5	6	7	8
	x	13,4	20,4	27,4	34,4	41,4	48,4	55,4
7	y	2	3	4	5	6	7	8
	x	9,5	21	33,75	48,2	64,5	82,71429	102,875
8	y	2	3	4	5	6	7	8
	x	7,5	15	21,75	28,2	34,5	40,71429	46,875
9	y	2,3	2,4	2,5	2,6	2,7	2,8	2,9
	x	0,29	0,76	1,25	1,76	2,29	2,84	3,41
10	y	0,1	0,2	0,3	0,4	0,5	0,6	0,7
	x	0,105	0,22	0,345	0,48	0,625	0,78	0,945
11	y	2,8	2,9	3	3,1	3,2	3,3	3,4
	x	4,496	9,527	15	20,933	27,344	34,251	41,672
12	y	2,4	2,5	2,6	2,7	2,8	2,9	3
	x	0,672	3,625	6,928	10,599	14,656	19,117	24
13	y	0,8	0,9	1	1,1	1,2	1,3	1,4
	x	1,096	2,427	4	5,833	7,944	10,351	13,072
14	y	2,4	2,5	2,6	2,7	2,8	2,9	3
	x	3,408	7,5	11,912	16,656	21,744	27,188	33
15	y	0,1	0,2	0,3	0,4	0,5	0,6	0,7
	x	0,963	0,864	0,721	0,552	0,375	0,208	0,069

 

Контрольные вопросы:                 

1) В каких случаях применяется интерполяция?

2) Опишите задачу интерполяции.

3) Вручную найдите значение функции в точке 2.5 () по данной таблице значений (таб. 3).

Таблица 3 - Корни и значения функции

Перечень вспомогательной литературы:

1. Шевченко Г.И. Численные методы. Теория, алгоритмы, программы: учебное пособие – Ставрополь: СКФУ, 2015. – 151 с;

2. Иванов А. П., Олемской И. В. Численные методы. Часть II: учебное пособие – Санкт-Петербург: 2012. – 80 с.

 

 

        III. Тема: Численное интегрирование

Цель: изучить методы численного интегрирования и овладеть практическими навыками их решения на языке программирования.

Теоретическая часть:

Задача численного интегрирования заключается в нахождении интеграла , для функции , заданной непрерывно на отрезке [a, b]. Графический смысл интегрирования заключается в нахождении площади (S) фигуры под графиком подынтегральной функции , заданной на отрезке [a, b]. На рисунке (рис. 1) функция  задана на отрезке [3.5, 7], значит площадь под функцией в этом отрезке будет равна ее интегралу.

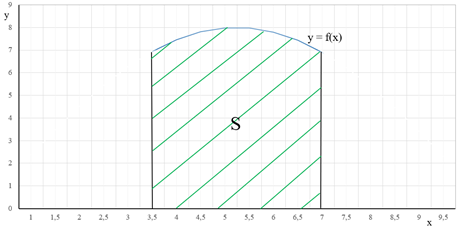
Рисунок 8 - Графический смысл

Численное интегрирование применяется для нахождения интегралов для непрерывных на отрезке [a, b] функций , которые имеют слишком сложную первообразную, или первообразную, которую нельзя выразить аналитически через элементарные функции; и для функций , которые известны только в нескольких точках, то есть заданных таблично.

Общий подход к решению задачи численного интегрирования имеет два этапа:

1. Разбиваем интервал [a, b] на множество более мелких равных интервалов;

2. Находим площади фигур на новых интервалах под графиком подынтегральной функции , суммируем их.

Существуют различные методы вычисления интегралов с помощью квадратурной формулы

                                        (3.1)

где  на отрезке [a, b].

Методы численного интегрирования, которые будут рассмотрены в данной лабораторной работе:

1)                Метод прямоугольников;

2)                Метод трапеций;

3)                Метод Симпсона.

1. Метод прямоугольников

Алгоритм метода прямоугольников является самым простым среди всех методов численного интегрирования. Сначала отрезок [a, b] разбивается на  равных частей шириной  - шаг разбиения:

Далее в качестве приближенного значения определенного интеграла берется интегральная сумма, которая находится при помощи квадратурной формулы.

В геометрическом смысле интеграл равен сумме площадей прямоугольников шириной  и высотой, определенной по следующим методам:

1. Метод левых прямоугольников

Это метод, в котором высота прямоугольников равна значению подынтегральной функции в левых концах каждого шага . Квадратурная формула:

где S – приближенное значение определенного интеграла.

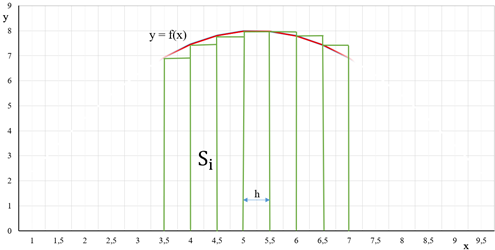
Рисунок 9 - Метод левых прямоугольников

2. Метод правых прямоугольников

Это метод, в котором высота прямоугольников равна значению подынтегральной функции в правых концах каждого шага . Квадратурная формула:

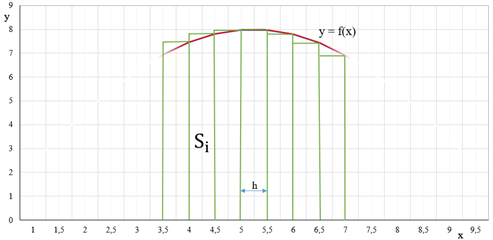
Рисунок 10 - Метод правых прямоугольников

3. Метод средних прямоугольников

Это метод, в котором высота прямоугольников равна значению подынтегральной функции в средней точке шага . Квадратурная формула:

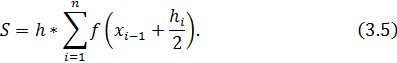
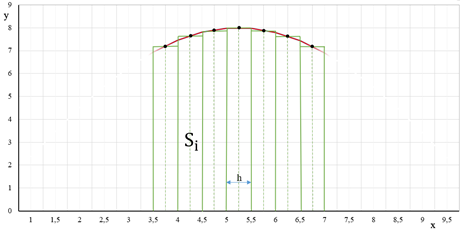
Рисунок 11 – Метод средних прямоугольников

Метод средних прямоугольников наиболее точный, так как не дает погрешности в расчетах из-за нарушения симметрии в построении прямоугольников.

При программировании данного метода лучше всего пользоваться данным порядком формул:

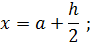
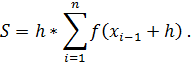
Суммирование происходит в цикле, за циклом происходит умножение суммы на шаг .

Формула прямоугольников имеет вторую степень точности , то есть при уменьшении  в 10 раз, погрешность расчёта интеграла уменьшается в 100 раз.

2. Метод трапеций

Алгоритм метода трапеций схож с алгоритмом метода прямоугольников. Сначала отрезок [a, b] разбивается на  равных частей шириной  - шаг разбиения:

в качестве узлов берутся границы отрезков.

В геометрическом смысле интеграл равен сумме площадей элементарных прямоугольных трапеций шириной  и высотой, равной:

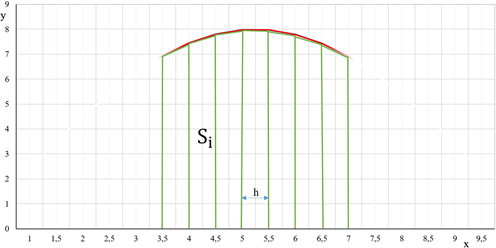
Рисунок 12 - Метод трапеций

Площадь каждой трапеции можно вычислить по формуле:

Таким образом, просуммировав все площади трапеций, получим формулу примерного расчета интеграла по методу трапеций:

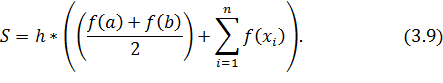
Суммирование происходит в цикле, за циклом происходит прибавление к сумме высоты трапеции, и далее умножение конечной суммы на шаг .

Формула трапеций имеет вторую степень точности , то есть при уменьшении  в 10 раз, погрешность расчёта интеграла уменьшается в 100 раз.

3. Метод Симпсона

В данном методе отрезок [a, b] разбивается на четное количество частей 2n. Ширина шага разбиения равна:

в качестве узлов берутся границы отрезков.

 

В геометрическом смысле интеграл равен сумме площадей элементарных прямоугольных трапеций шириной  и высотой, равной:

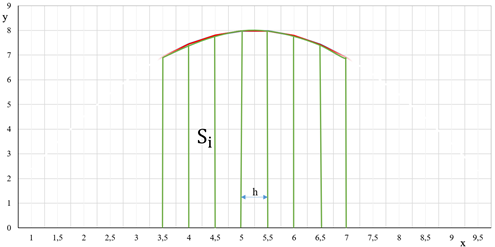
Рисунок 13 - Метод Симпсона

Для каждой пары отрезков [a, b] подынтегральная функция приближённо заменяется параболой, проходящей через 3 точки: границы и середина отрезка. Парабола задается функцией:

Площадь под параболой равна:

Суммируя все параболы, можно получить формулу для примерного расчета интеграла по методу Симпсона:

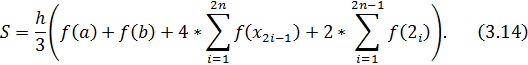
Сумма, которая умножается на 4, суммирует функции с нечетными корнями. Другая, которая умножается на 2, суммирует функции с четными корнями.

Формула Симпсона имеет четвертую степень точности , то есть при уменьшении  в 10 раз, погрешность расчёта интеграла уменьшается в 10000 раз.

Оценка погрешности:

Оценка погрешности может проводиться двумя способами, отличными точностью ответа:

a) Известен точный ответ

 – точный ответ (посчитанный вручную);

 – приблизительный ответ (посчитанный численным методом).

Абсолютная погрешность:

Относительная погрешность:

b) Точный ответ не известен

Необходимо повторить расчет дважды с шагом:

- h, n разбиений (Ih);

- , 2n разбиений ().

Абсолютная погрешность по формуле Рунге:

где k – порядок точности метода. Методы имеют данные порядки точности k:

- 2 для метода прямоугольников и трапеций;

- 4 для метода Симпсона.

Относительная погрешность:

Уточненное значение с учетом знака:

 

Практическое задание:

1) Напишите программу для вычисления интеграла функции в отрезке [a, b], с шагом h по методу серединных прямоугольников, трапеций и Симпсона. В программе должна считаться абсолютная погрешность каждого метода по формуле Рунге и относительная погрешность. По значениям погрешности программа должна выводить название самого эффективного метода и его погрешности.

2) Ответьте на контрольные вопросы.

3) Оформите отчет по требованиям, и отправьте его и программу на почту преподавателю.

Примерное время выполнения задания – 6 часов.

Функцию, отрезок и шаг необходимо взять из списка, приведенного ниже. Номер варианта должен соответствовать порядковому номеру в списке группы.

Контрольные вопросы:

1. Какой геометрический смысл имеет интеграл? В общем смысле, в методе прямоугольников, трапеций и Симпсона.

2. Какой метод имеет самую высокую степень погрешности по h?

3. От чего зависит высота прямоугольников в методе прямоугольников?

4. Когда применяется численное интегрирование?

Перечень вспомогательной литературы:

1. Шевченко Г.И. Численные методы. Теория, алгоритмы, программы: учебное пособие – Ставрополь: СКФУ, 2015. – 151 с;

2. Чузлов В. А. Численные методы интегрирования и решения обыкновенных дифференциальных уравнений: курс лекций – Томск: 2022. – 42 с;

3. Соловьев, В. П. Основы численных методов: учеб.-метод. пособие / В. П. Соловьев, Т. М. Кривоносова, В. Л. Смирнов. – Минск: БГУИР, 2011. – 131 с.

         IV. Тема: Одномерная оптимизация

Цель: изучить методы одномерной оптимизации и овладеть практическими навыками их решения на языке программирования.

Теоретическая часть:

Одномерная оптимизация – это процесс нахождения экстремума функции одной переменной. Пусть  – функция, определенная на промежутке [a, b]. Функцию  называют унимодальной, если на отрезке [a, b] существует единственная точка х, в которой  принимает экстремальное значение. Если функция берется с минусом , то будет решена задача поиска максимума функции, если функция берется с плюсом – то задача минимума функции. В данной лабораторной работе будет рассмотрена задача поиска минимума функции.

Нахождение точки минимума можно разделить на два этапа:

1) Точка минимума отделяется: определяется отрезок, который содержит одну точку минимума;

2) Уточняется до требуемой точности значение минимума функции на отрезке.

Определить отрезок, в котором находится одна точка минимума функции можно графическим способом и с помощью методов.

1. Определение отрезка с точкой минимума функции алгоритмом Свена

Входные данные: начальное приближение и шаг.

Выходные данные: границы отрезка, в котором находится точка минимума функции.

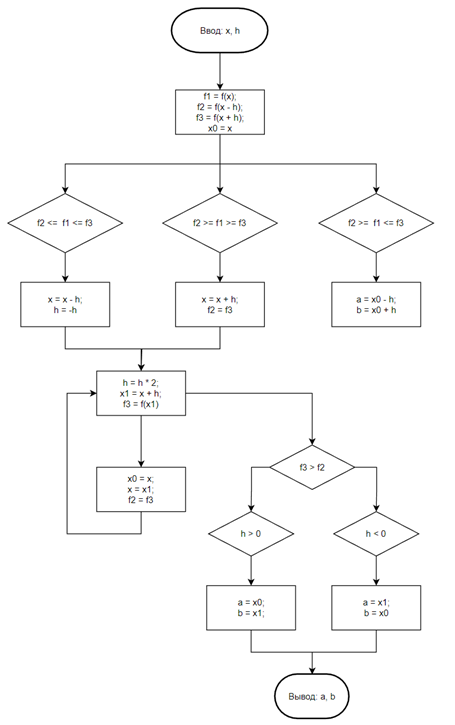
Рисунок 14 - Алгоритм Свена

2. Уточнение до требуемой точности значение минимума функции на отрезке.

Когда был определен отрезок [a, b], в котором содержится точка минимума функции, ее можно уточнить до требуемой точности  с помощью численных методов одномерной оптимизации. В данной лабораторной работе будет рассмотрен метод золотого сечения.

Золотым сечением отрезка называется деление его на две части так, чтобы отношение длины всего отрезка к длине большей части ровнялось отношению дины большей части к длине меньшей части. Данному определению соответствуют две точке на отрезке: y, z:

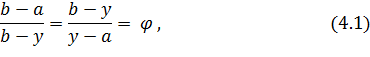
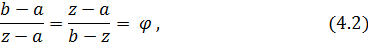
где  – пропорция золотого сечения.

Рисунок 15 - Расположение точек золотого сечения на отрезке

Из уравнений (4.1), (4.2) можно найти значения пропорции золотого сечения (), y, z:

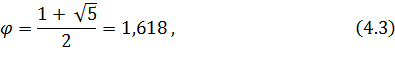
Точка y дает золотое сечение для отрезка [a, z], а точка z дает золотое сечение для отрезка [y, b]. Из этого заключения можно построить итерационный процесс, в котором на каждой итерации необходимо будет рассчитывать только одну новую точку. На каждой итерации функция от точки должна вычисляться только один раз.

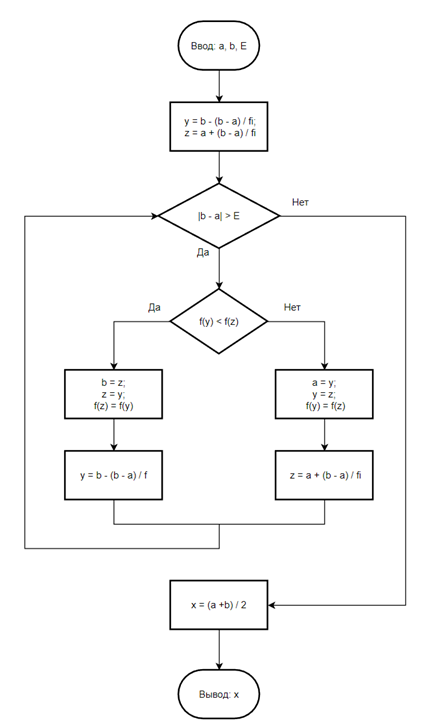
Рисунок 16 - Алгоритм метода золотого сечения

Практическое задание:

1) Напишите программу для нахождения минимума функции одной переменной. В программе должен быть реализован алгоритм для поиска отрезка, содержащего минимум, и метод золотого сечения. Точность .

2) Также необходимо изучить как влияют различные значения начального приближения и шага на точность вычислений. Точность вычислений считается от точного значения минимума функции, рассчитанного самостоятельно в интернет-ресурсах. Проведите 10 экспериментов с различными значениями.

3) Ответьте на контрольные вопросы.

4) Оформите отчет по требованиям, и отправьте его и программу на почту преподавателю.

Примерное время выполнения задания – 6 часов.

Функцию необходимо взять из списка, приведенного ниже. Номер варианта должен соответствовать порядковому номеру в списке группы.

Контрольные вопросы:

1. Какая цель применения алгоритма Свена?

2. При каких условиях решается задача поиска минимума и максимума функции?

3. Как графическим способом можно определить точку минимума?

4. Подумайте и напишите можно ли графическим способом определить точку минимума функции?

Перечень вспомогательной литературы:

1. Т. М. Попова. Методы одномерной оптимизации: методические указания и задания к выполнению лабораторных работ по дисциплине «Методы оптимизации» – Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2011. – 26 с.

2. Studfiles. Файловый архив студентов / МетодЫ решения оптимизационной задачи: портал. – Санкт-Петербург, 2014. – URL: https://studfile.net/preview/1169714/

 

            V. Тема: Многомерная оптимизация

Цель: изучить методы многомерной оптимизации и овладеть практическими навыками их решения на языке программирования.

Теоретическая часть:

Многомерная оптимизация – это процесс нахождения экстремума функции многих переменных. Пусть  – функция многих переменных, необходимо определить значения вектора переменных , при котором функция принимает максимальное или минимальное значение. Вектор переменных  можно рассматривать как точку (элемент) n-мерного линейного пространства независимых переменных  . Операции сложения и вычитания можно производить по правилам векторов.

Если нет ограничений на параметры  – это глобальная безусловная минимизация, если есть ограничения – это условная минимизация. В данной лабораторной работе будет разобраны методы глобальной безусловной минимизации:

1) Метод покоординатного спуска;

2) Метод градиентного (наискорейшего) спуска.

1. Метод покоординатного спуска

Метод покоординатного спуска является одним из простейших методов многомерной оптимизации и неплохо справляется с поиском локального минимума функций с относительно гладким рельефом, поэтому знакомство с методами оптимизации лучше начинать именно с него.

Поиск экстремума ведется в направлении осей координат, т.е. в процессе поиска изменяется только одна координата. Таким образом, многомерная задача сводится к одномерной.

Суть метода заключается в поочередном поиске минимума функции по одной из координат, полагая, что другие координаты фиксированы какими-то начальными значениями. Таким образом получаем задачу поиска минимума одномерной функции.

Алгоритм:

1) Выбирается начальное приближение  и задается точность ;

2) Фиксируются значения всех переменных кроме , получается функция одной переменной ;

3) Минимизируется одномерным методом оптимизации функция одной переменной – получается точка ;

4) Возвращаемся на 2 пункт, фиксируем все значения кроме , повторяем действия с данной точкой;

5) Процесс продолжается, пока расстояние между 2 точками не станет меньше точности;

6) Возвращается текущее значение ;

Достоинства метода:

1) Простота при определении перемещения в пространстве переменных;

2) Для гладких функций метод обеспечивает сходимость к точке локального минимума;

3) Возможность использования простых методов одномерной оптимизации.

Недостатки метода:

1) Обычно не высокая скорость сходимости;

2) Процесс может не сходиться при наличии оврагов.

2. Метод градиентного (наискорейшего) спуска

Метод градиентного спуска — численный метод нахождения локального минимума или максимума функции с помощью движения вдоль градиента. Градиент – это вектор, показывающий направление наискорейшего роста функции в данной точке:

или

где частное – это частные производные функции , а i, j, k – это базис декартовой системы координат. Градиент функции в точке показывает направление наибольшего роста функции.

Антиградиент () – это направление наискорейшего убывания функции в данной точке. Единичный вектор в направлении наискорейшего убывания:

Градиент от функции равен нулю в точке минимума, это и будет служить условием окончания итерационного процесса.

В алгоритме градиентного спуска необходим расчёт производной по переменным функции. Ниже представлен алгоритм метода для функции с двумя переменными .

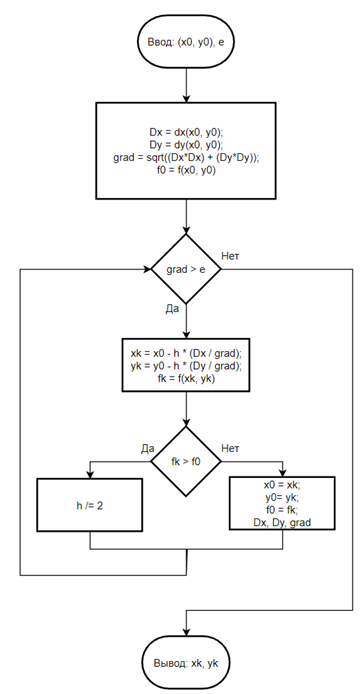
Рисунок 17 - Алгоритм градиентного спуска

Очень важен выбор величины h, если она слишком маленькая процесс сходится медленно (медленно происходит поиск минимума функции), если слишком большая процесс расходится.

Существует способ подбора шага. В начале берется большое значение h, но если , то нужно вернуться в предыдущую точку и уменьшить h вдвое. То есть  при .

Достоинства:

1) Быстрая сходимость.

Недостатки:

1) Требуется знание частных производных; если невозможно получить аналитические выражения для частных производных, их нужно считать численно;

2) Процесс может не сойтись при неудачном начальном приближении (x0, y0);

3) Нужен контроль количества итераций;

4) Если фикция имеет много локальных минимумов, то минимизацию повторяют многократно, беря в качестве начальных приближений случайные числа.

Практическое задание:

1) Проведите предварительный анализ функции, для нахождения отрезка, в котором находится минимум функции.

2) Напишите программу для нахождения минимума функции двух переменных. В программе должны быть реализованы метод покоординатного спуска и метод градиентного (наискорейшего спуска). Точность . Программа должна считать количество итераций каждого метода и выводить, какой метод быстрее.

3) Ответьте на контрольные вопросы.

4) Оформите отчет по требованиям, и отправьте его и программу на почту преподавателю.

Примерное время выполнения задания – 6,5 часов.

Функцию необходимо взять из списка, приведенного ниже. Номер варианта должен соответствовать порядковому номеру в списке группы.

1.

2.

Контрольные вопросы:

1. Что такое условная минимизация?

2. Сколько переменных может быть при многомерной оптимизации?

3. Суть покоординатного спуска.

4. С помощью чего находится локальный минимум при градиентном спуске? Дайте определение.

Перечень вспомогательной литературы:

1. Т. М. Попова. Методы многомерной оптимизации: методические указания и задания к выполнению лабораторных работ по дисциплине «Методы оптимизации» для студентов направления «Прикладная математика» – Хабаровск: Изд-во Тихоокеан. гос. ун-та, 2012. – 44 с.

2. Прокопенко Н. Ю. Методы оптимизации [Текст]: учеб. пособие /Н. Ю. Прокопенко; Нижегор. гос. архитектур. - строит. ун-т. – Н. Новгород: ННГАСУ, 2018. – 118 с.

 

3. Скачано с www.znanio.ru