Министерство образования и науки Челябинской области

государственное бюджетное профессиональное образовательное         учреждение

«Каслинский промышленно-гуманитарный техникум»

Верхнеуфалейский филиал

 

 

 

КОМПЛЕКТ КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ

 

 

по учебной дисциплине

ОУДБ.04 « Математика»

основной профессиональной образовательной программы

по профессии

43.01.09. «Повар-кондитер»

 

 

2019 год

СОГЛАСОВАНО  на заседании предметно-цикловой комиссии Протокол № ____ от «___» ___________ 2019  г. Председатель ПЦК: _________

УТВЕРЖДАЮ: Зам. директора по учебной работе  ГБПОУ «КПГТ» _____________ Н.Н. Ефанова

 

 

Комплект контрольно-оценочных средств разработан на основе Федерального государственного образовательного стандарта среднего профессионального образования по профессии  43.01.09 «Повар-кондитер» по учебной дисциплине ОУДБ.04. «Математика»

 

 

 

 

 

Организация - разработчик:

Государственное бюджетное профессиональное образовательное учреждение «Каслинский промышленно-гуманитарный техникум» Верхнеуфалейский филиал

 

 

Разработчик: Хусаинов В.Г., преподаватель ГБПОУ «Каслинский промышленно-гуманитарный техникум» Верхнеуфалейский филиал

 

 

СОДЕРЖАНИЕ

 

1	Паспорт комплекта контрольно-оценочных средств	4
2	Результаты освоения учебной дисциплины	7
3	Оценка освоения учебной дисциплины	15
3.1	Формы контроля и оценивания элементов учебной дисциплины	15
3.2	Типовые задания для оценки освоения учебной дисциплины	16
3.2.1	Входной контроль	16
3.2.2	Задания для промежуточного тематического контроля (контрольные работы).
3.2.3	Задания для итогового контроля (экзамен).	76
4	Критерии оценивания.	85
5	Учебно-методическое и информационное обеспечение дисциплины	88

 

 

    

 

 

1.ПАСПОРТ КОМПЛЕКТА КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ         

         В результате освоения учебной дисциплины математика обучающийся должен обладать предусмотренными  ФГОС по профессии СПО код 19.01.17. (260807.01) «Повар, кондитер» следующими умениями, знаниями, которые формируют профессиональную компетенцию, и общими компетенциями:

Знать, понимать:

З-1. Значение математической науки для решения задач, возникающих в теории и практике, широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе.

З-2. Знание практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа; создания математического анализа; возникновения и развития геометрии.

З-3.Универсальный характер законов развития математических рассуждений; их применимость во всех областях человеческой деятельности.

З-4. Вероятностный характер различных процессов окружающего мира

Уметь:

 

·               У-1.выполнять арифметические действия над числами, сочетая устные и письменные приемы; находить приближенные значения величин и погрешности вычислений (абсолютная и относительная); сравнивать числовые выражения;

·               У-2.находить значения корня, степени, логарифма, тригонометрических выражений на основе определения, используя при необходимости инструментальные средства; пользоваться приближенной оценкой при практических расчетах;

·               У-3.выполнять преобразования выражений, применяя формулы, связанные со свойствами степеней, логарифмов, тригонометрических функций;

У-4.вычислять значение функции по заданному значению аргумента при различных способах задания функции;

·               У-5.определять основные свойства числовых функций, иллюстрировать их на графиках;

·               У-6.строить графики изученных функций, иллюстрировать по графику свойства элементарных функций;

·               У-7.использовать понятие функции для описания и анализа зависимостей величин;

·               У-8 находить производные элементарных функций;

·               У-9.использовать производную для изучения свойств функций и построения графиков;

·               У-10.применять производную для проведения приближенных вычислений, решать задачи прикладного характера на нахождение наибольшего и наименьшего значения;

·               У-11.вычислять в простейших случаях площади и объемы с использованием определенного интеграла;

 

У-12.решать рациональные, показательные, логарифмические, тригонометрические уравнения, сводящиеся к линейным и квадратным, а также аналогичные неравенства и системы;

·               У-13.использовать графический метод решения уравнений и неравенств;

·               У-14.изображать на координатной плоскости решения уравнений, неравенств и систем с двумя неизвестными;

·               У-15.составлять и решать уравнения и неравенства, связывающие неизвестные величины в текстовых (в том числе прикладных) задачах.

У-16.решать простейшие комбинаторные задачи методом перебора, а                          также с использованием известных формул;

·               У-17.вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;

·               У-18.распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;

·               У-19.описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;

·               У-20.анализировать в простейших случаях взаимное расположение объектов в пространстве;

·               У-21.изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;

·               У-22.строить простейшие сечения куба, призмы, пирамиды;

·               У-23.решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);

·               У-24.использовать при решении стереометрических задач планиметрические факты и методы;

·               У-25.проводить доказательные рассуждения в ходе решения задач;

 

·               Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:

 

для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;

         для описания при помощи функций различных  зависимостей, представления их графически,  интерпретаций графиков;

для решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.

   для построения и исследования простейших математических моделей.

для анализа реальных числовых данных, представленных в виде диаграмм, графиков; анализа информации статистического характера.

       для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;

 вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.

Развивать способности для формирования общих компетенций:

Развивать способности для формирования общих компетенций:

ОК-1.Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес;

ОК-2.Организовывать собственную деятельность, выбирать типовые методы и способы выполнения практических задач; оценивать их эффективность и качество.

ОК-3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

ОК-4.Осуществлять поиск и использование информации, необходимой для эффективного использования профессиональных задач, профессионального и личностного развития.

ОК-5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

ОК-6 .Работать в коллективе и в команде, эффективно общаться с руководством, с коллегами, с потребителями.

ОК-7.Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

ОК-8. Самостоятельно выполнять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

ОК-9.Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

ОК-10.Соблюдать действующее законодательство и обязательные требования нормативно правовых документов, а также требования стандартов и иных нормативных документов.

 

Формой аттестации по учебной дисциплине является  письменный экзамен.

 

2. Результаты освоения учебной дисциплины, подлежащие проверке

2.1. В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений и знаний, а также динамика формирования общих компетенций:

 

Формой аттестации по учебной дисциплине является  экзамен.

 

3. ОЦЕНКА ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ:

3.1. ФОРМЫ КОНТРОЛЯ И ОЦЕНИВАНИЯ ЭЛЕМЕНТОВ УЧЕБНОЙ ДИСЦИПЛИНЫ

Предметом оценки служат умения и знания, предусмотренные ФГОС по дисциплине «математика», направленные на формирование общих и профессиональных компетенций. Итоговой аттестацией по учебной дисциплине является  письменный экзамен.

 

Предметом оценки освоения дисциплины являются умения, знания, общие компетенции, способность применять их в практической деятельности и повседневной жизни.

 

Знание основ

математики

«5» - 100 – 90% правильных ответов

«4» - 89 - 80% правильных ответов

«3» - 79 – 70% правильных ответов

«2» - 69% и менее правильных ответов 2

 

Контрольная работа

Знание основ математики в соответствии с пройденной темой и умения применения знаний на практике

«5» - 100 – 90% правильных ответов

«4» - 89 - 80% правильных ответов

«3» - 79 – 70% правильных ответов

«2» - 69% и менее правильных ответов 4

 

Практические занятия

Умение применять полученные знания на практике.

«5» - 100 – 90% правильных ответов

«4» - 89 - 80% правильных ответов

«3» - 79 – 70% правильных ответов

«2» - 69% и менее правильных ответов 5

 

Составление конспектов, рефератов, творческих работ.

Умение ориентироваться в информационном пространстве, составлять конспект.

Знание правил оформления рефератов, творческих работ.

Соответствие содержания работы, заявленной теме, правилам оформления работы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.2	ТИПОВЫЕ ЗАДАНИЯ ДЛЯ ОЦЕНКИ ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ
3.2.1	ВХОДНОЙ КОНТРОЛЬ

 

Контрольная работа № 1 (нулевой срез)

 

Вариант 1

1.     Решить уравнение: 2х² + 3х – 5 = 0.

2.     Решить систему уравнений:     3х – у = 3,

                                                   3х – 2 у = 0.

3.   Решить неравенство: 6х – 5(2х + 8)14 + 2х.

4.     Найти 15% от числа 80.

5.     Выполните действие, и результат запишите в виде десятичной дроби:

(1,2  ) (3  ).

Вариант 2

1.     Решить уравнение: 5х² - 7х + 2 = 0.

2.     Решить систему уравнений:     2х + у = 1,

                                                   5х + 2 у = 0.

3.   Решить неравенство: 5 + х  3х - 3(4х + 5).

4.     Найти 45% от числа 90.

5.     Выполните действие, и результат запишите в виде десятичной дроби:

(1,6 ) (4  10²).

 

Вариант 3

1.     Решить уравнение: 3х² - 5х - 2 = 0.

2.     Решить систему уравнений:       х + 5у = 7,

                                                   3х + 2 у = -5.

3.   Решить неравенство:  3(3х - 1)2(5х - 7).

4.     Найти 40% от числа 120.

5.     Выполните действие, и результат запишите в виде десятичной дроби:

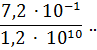
Вариант 4

1.     Решить уравнение: 2х² - 7х + 3 = 0.

2.     Решить систему уравнений:     2х - 3у = 1,

                                                   3х +  у = 7.

3.   Решить неравенство: 5(х + 4)2(4х - 5).

4.     Найти 30% от числа 240.

5.     Выполните действие, и результат запишите в виде десятичной дроби:

ОТВЕТЫ  к  контрольной  работе    № 1

 

№ варианта	Задание 1	Задание 2	Задание 3	Задание 4	Задание 5
1	-2,5; 1	(2;3)	х<-9	12	3,6∙10-4= 0,00036
2	0,4; 1	(-2;5)	х>-2	40,5	6,4∙10-3= 0,0064
3	; 2	(-3;2)	х<11	48	6∙10-11= 0,00000000006
4	0,5; 3	(2;1)	х<10	72	0,8∙10-2= 0,008

 

ЗАЧЁТ по повторению

Вариант 1

1.     Решить уравнение: 3х² + 8х – 3 = 0.

2.     Решить систему уравнений:     3х – 2у = 5,

                                                   2х + 5 у = 16.

3.   Решить неравенство: 2х – 3(х + 1)2 + х.

4.     Найти 15% от числа 70.

5.     Выполните действие, и результат запишите в виде десятичной дроби:

(1,2  ) (4  ).

Вариант 2

1.     Решить уравнение: 5х² - 7х + 2 = 0.

2.     Решить систему уравнений:     2х + 3у = -7,

                                                   х -  у = 4.

3.     Решить неравенство: 25 -  х > 2 - 3(х - 6).

4.     Найти 25% от числа 120.

5.     Выполните действие, и результат запишите в виде десятичной дроби:

(1,4 ) (3 10²).

Вариант 3

1.     Решить уравнение: 9х² - 6х + 1 = 0.

2.     Решить систему уравнений:      2х - у = 13,

                                                   2х + 3 у = 9.

3.   Решить неравенство:  2(х - 1)5х - 4(2х + 1).

4.     Найти 60% от числа 120.

5.     Выполните действие, и результат запишите в виде десятичной дроби:

        .

Вариант 4

1.     Решить уравнение: 6х² - 7х + 1 = 0.

2.     Решить систему уравнений:      2х - 3у = 1,

                                                   3х +  у = 7.

3.     Решить неравенство:  2(1 - х) ≥ 5х - (3х + 2).

4.     Найти 20% от числа 150.

Выполните действие, и результат запишите в виде десятичной дроби:
   

ОТВЕТЫ  к проверочной работе ЗАЧЁТ по повторению

№ варианта	Задание 1	Задание 2	Задание 3	Задание 4	Задание 5
1	3;	(3;2)	х < -2,5	10,5	4,8∙10-4= 0,00048
2	0,4; 1	(1;-3)	х > -2,5	30	4,2∙10-3= 0,0042
3		(2;1)	х > -	72	3∙10-4= 0,0003
4	1;	(2;1)	х ≤ 0	30	4∙10-5= 0,00004

 

3.2.2 ЗАДАНИЯ ДЛЯ ПРОМЕЖУТОЧНОГО ТЕМАТИЧЕСКОГО КОНТРОЛЯ (КОНТРОЛЬНЫЕ РАБОТЫ).

Самостоятельная работа № 1

                                                    ЗАЧЁТ:

 Действительные и комплексные числа

ВАРИАНТ 1

1.     Дайте определение действительных чисел.

2.     Дайте определение абсолютной погрешности приближённого числа.

3.     Вычислить:

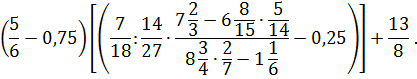
4.     При взвешивании купленного риса  получилось 3,5 кг, причём известно, что предельная абсолютная погрешность равна  14 г. Определить предельную относительную погрешность и границы истинного значения (А) массы купленного риса.

5.   Найти значение выражения  если

 . 

 

 

ВАРИАНТ 2

1.     Дайте определение комплексных чисел.

2.     Дайте определение относительной погрешности приближённого числа.

3.     При взвешивании купленного винограда  получилось 6,6 кг, причём известно, что предельная абсолютная погрешность равна  33 г. Определить предельную относительную погрешность и границы истинного значения (А) массы купленного винограда.

4.     Вычислить:

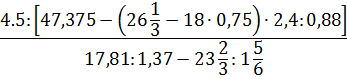
5.   Найти значение выражения  если

 . 

 

 

ОТВЕТЫ  к ЗАЧЁТУ «Действительные и комплексные числа»

 

№ задания	Вариант 1	Вариант 2
1	Совокупность всех рациональных и всех иррациональных чисел образует множество действительных чисел.	Числа вида z=a+bi , где а и b –        действительные числа и i2=-1 называются комплексными числами.
2	Величина =, где А – точное значение числа; а – его приближённое значение, называется абсолютной величиной погрешности числа а.	Относительной погрешностью числа  называется отношение абсолютной погрешности к абсолютной величине приближённого значения.
3	1)  А=3,5 кг=3500г; 14 г; 2)    Истинное значение массы А=3500 г (14 г) или  А=3500 г	1)   А=6,6 кг=6600г; 33 г; 2)      Истинное значение массы А=6600 г (33 г) или  А=6600 г
4	2	4
5	=  = =	=  = =

 

 

 

  Контрольная работа  № 2  «ЛОГАРИФМЫ»

Вариант 1

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   log₂ (4х - 1)= 3;

    б)    log₇ 2 = 1- log₇ (5 - х).      

4. Решите неравенства:

    а)   log₅ (1 - 4х) ≤ 2; 

    б)    log(2х + 3) > -3.  

 

Вариант 2

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   log₄  (2х - 1)= 2; 

    б)    log₂ (2х + 3) = log ₂ 4 + 1.      

4. Решите неравенства:

    а)   log₃ (2 - 3х) ≥  2; 

    б)    (х + 1) > -2.  

 

Вариант 3

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   log₅  (6х - 1)= 2; 

    б)    log₃ (4х + 5) = log₃ 9 + 1.      

4. Решите неравенства:

    а)   log₄ (2 - 5х) ≥  3; 

    б)    (х - 1) > -1.  

Вариант 4

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   log₃  (7х - 2)= 2; 

    б)    log₇ (2х + 5) = log₇49 + 2.      

4. Решите неравенства:

    а)   log₄ (5 - х) ≥ 0; 

    б)    (3х - 1) > - 1 .  

  Вариант 5

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   (х - 2)= - 2; 

    б)    log₅ (2х - 3) = log₅25 - 2.      

4. Решите неравенства:

    а)   log₉ (3 - х) ≤ 0; 

    б)    (3х - 1) < - 1 .  

Вариант 6

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   (х - 2)= - 3; 

    б)    log₈ (2х - 3) = log₈1 - 1.      

4. Решите неравенства:

    а)   log₄ (8 - х) ≤ 2; 

    б)    (2х - 1) < 0 .  

Вариант 7

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   (2х - 1)= - 4; 

    б)    log₃ (х - 3) = log₃27 - 1.      

4. Решите неравенства:

    а)   log₅ (5 - х) ≤ 2; 

    б)    (х + 3) < - 1 .  

Вариант 8

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   (х - 2)= 0; 

    б)    log₃ (х + 9) = log₃81 - 3.      

4. Решите неравенства:

    а)   log₅ (х - 6) ≤ 2; 

    б)    (х + 5) > - 2 .

  Вариант 9

1. Вычислите   .

2. Найдите область определения функции     у = lg.

3. Решите уравнения:

    а)   log₈  (5х - 2)= 1; 

    б)    log₆ (х + 5) = log₆ 36 + 1.      

4. Решите неравенства:

    а)   log₅ (3 - х) ≥ 0; 

 

Ответы к контрольной работе № 9 «Логарифмы»

№ задания	Вариант 1	Вариант 2	Вариант 3	Вариант 4	Вариант 5	Вариант 6	Вариант 7	Вариант 8	Вариант 9
1	5	4	7	3	8	11	12	13	9
2	(-∞;-)  (1; ∞)	(-∞;-2) (;∞)	(-∞;-) (0,4;∞)	(-∞;-3,5) (5;∞)	(-;7)	(;2,5)	(-∞;-3) (;∞)	(-∞;-1,5) (;∞)	(-∞;-0,5) (9;∞)
3 а)		8,5			18	10	8,5	3	2
3 б)		2,5	5,5	1198	2		12	-6	211
4 а)	[-6;)	(-∞;-]	(-∞;-12,4]	(-∞;4]	[2;3)	[-8;8)	[-20;5)	(6;31]	(-∞;2]
4 б)	(-1,5;2,5)	(-1;24)	(1; 7)	(;)	(;∞)	(1; ∞)	(6; ∞)	(-5;76)	(1;17)

 

 

Зачёт   «Свойства логарифмов и логарифмической функции»

Вариант 1

 

1.       Дайте определение логарифма данного числа по данному основанию.

2.     

4.   Найдите х, если

5.   Вычислите   .

 

 

Вариант 2

1.       Сформулируйте основные свойства логарифмов.

2.      .

3.   Вычислите:      

4.   Найдите х, если

5.   Вычислите   .

 

 

Вариант 3

1.   Какая функция называется логарифмической? Сформулируйте основные свойства логарифмической функции при а>0.

2.   .

4.   Найдите х, если

5.   Вычислите   .

 

Вариант 4

1.   Запишите основное логарифмическое тождество.

2.    .

3.   Вычислите:      

4.   Найдите х, если

5.   Вычислите   .

 

 

 

ОТВЕТЫ  к  зачёту   «Свойства логарифмов и логарифмической функции»

№ варианта Задание №	Вариант 1	Вариант 2	Вариант 3	Вариант 4
1.	Логарифмом числа в по осно-ванию а называ-ется показатель степени, в кото-рую нужно воз-вести основание а, чтобы полу-чить число в. =в.	1) 2) 3) 4) 5)	Функцию, задан- ную формулой называют лога-рифмической функцией с ос-нованием а.	1) D( 2) Е(= . 3)  Логарифми- ческая функция на всей области определения возрастает  (при а>0)  или убывает (при  0<а<1).
2.	(	(-1;4)	(-∞;-5)(∞)	(-∞;-1)(∞)
3.	а) 4; б) -4; в) 15; г) 12; д) 1,5.	а) -2; б) 4; в) 125; г) 75;      д) .	а) 2; б) -2; в) 3; г) 20;      д) 8.	а) -5; б) 3; в) 7; г) ;      д) 48.
4.		5	21	10
5.	1		2

 

 

 

Контрольная работа № 3

«РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ»

Вариант 1

1.     Вычислить     arccos(-) - arcsin.

2.     Решить неравенство    tg х ≤ -1.

3.     Решить уравнения

     а) tg=0;

          б) sin²х - sin х=0;

          в) cos²х + cos х – 2 =0.

 

Вариант 2

1.     Вычислить     arctg (-) - arcsin.

2.     Решить неравенство    cos х < 0.

3.     Решить уравнения

     а) cos (х -) =;

          б) tg²х - tg х=0;

          в) sin ²х + sin х – 2 =0.

 

Контрольная работа № 4 «ПРОИЗВОДНАЯ И ЕЁ ПРИМЕНЕНИЕ»

Вариант 1

1. Решить неравенство      ≥ 0.

2. Тело движется по закону           х(t)=t³-2t² +5   (х – в метрах, t – в секундах).          Найдите скорость и ускорение тела через 2с после начала движения.

3. Исследовать функцию  f(х)= х² + 7х – 4   на монотонность и экстремумы.

4. Найти наибольшее и наименьшее значения функции       f(х)= х³- 6 х²      на

отрезке  [-2;5].

5. Составьте уравнение касательной к графику функции  f(х)= х² + 2х   в точке  х₀=1.

 

 

Вариант 2

1. Решить неравенство       ≤ 0.

2. Тело движется по закону           х(t)=  + 6t - 1   (х – в метрах, t – в секундах).       Найдите скорость и ускорение тела через 5с после начала движения.

3. Исследовать функцию   f(х)=10 – 4х -  х²   на монотонность и экстремумы.

4. Найти наибольшее и наименьшее значения функции       f(х)= х³- х      на

отрезке  [0;4].

5. Составьте уравнение касательной к графику функции   f(х)= х²-3х+2   в точке  х₀=

 

 

ОТВЕТЫ к контрольной работе «ПРОИЗВОДНАЯ И ЕЁ ПРИМЕНЕНИЕ»

№ задания	Вариант 1	Вариант 2
1	[0;](7; ∞)	(-∞;0][5;12)
2	4м/с; 8м/с2	31м/с; 10м/с2
3	f ↓ на х(-∞;-3,5),  f ↑ на х (-3,5; ∞) х=-3,5 точка  min	f ↑ на х(-∞;-2),  f ↓ на х (-2; ∞) х=-2 точка  max
4	уmax=0;    уmin=-32               [-2;5]                [-2;5]	уmax=;    уmin= -;             [0;4]                      [0;4]
5	у=4х-1	у =1-5х

 

Самостоятельная работа «Первообразная и интеграл» Вариант 1
1.       Найти общий вид первообразных: 1)    ; 2)  3)  4)  5)     .	2.  Вычислить интегралы: 1)     2)     3)     . 4)     5)

 

Самостоятельная работа «Первообразная и интеграл» Вариант 2
1.     Найти общий вид первообразных: 1)       ; 2)    3)    4)    5)        .	2.  Вычислить интегралы: 1)     ; 2)    ; 3)      ; 4)      ; 5)        .

 

ОТВЕТЫ к самостоятельной работе «Первообразная и интеграл»
	Вариант1	Вариант 2
1.	1)  ;   2)  3)  4)    5)     .	1)  ;   2)    3)  4)    5)   .
2.	1)    ; 2)     1 ; 3)     ; 4)   ; 5)     2.	1)    0 ;                   4)  25,5 ;       5)  5.

 

 

                       Контрольная работа № 5: «Первообразная и интеграл»

Вариант 1

 

1.                 Найти общий вид первообразных для функции

a)        f(x)= 4sin x + cos3x ;

б) f(x)= x² + 2x .

2.       Найти первообразную функции   f(x)=5х + x², график которой       проходит через точку  (1;3).

 

3.       Вычислить интеграл   х² +х)dx.

4.      Вычислить площадь фигуры, ограниченной линиями

         у = 3- х  и  у = - х²+2х+3.

                             

Вариант2

1.                                         Найти общий вид первообразных для функции

а) f(x)= 3cos x + sin4x;

б) f(x)= х⁵ + x² .

2.       Найти первообразную функции   f(x)=3x²-5, график которой       проходит через точку  (2;10).

3.       Вычислить интеграл    х² +2х)dx

4.      Вычислить площадь фигуры, ограниченной линиями

         у = 3+2х  и  у = х²-2х+3.

 

Ответы к контрольной работе № 2: «Первообразная и интеграл»

№ варианта	Задание 1 а)	Задание 1 б)	Задание 2	Задание 3	Задание 4
1	- 4 + +С	+ С	+	3	4,5
2		+ С	х3- 5х +12	1	10

ТЕСТЫ ПО МАТЕМАТИКЕ

ТЕМА: «Первообразная и интеграл

ВАРИАНТ № 1

Задание	Вариант ответа
1.     Среди заданных функций G(x), F(x) и H(x) выберете первообразную для функции                               у = -7 х3	а) G(x)= -21 х2 б) F(x)= -7 х4 в) H(x)=  -  7/4 х4
2.     Укажите ту функцию, для которой       F(x)= х3 + 3x + С        имеет общий вид первообразной	а) g(x)= 3 х2 + 3 б) h(x)= 3 х2 + 3x + 9 в) φ(x)=  х4/4 + 3
3.     Найдите общий вид первообразных для функции  f(x) =    4 sin x + 2 cos x	а) F(x)= 4cos x – 2sin x + С б) F(x)= - 4cos x + 2sin x + С в) F(x)=  - 4cos x + 2sin x
4.     Найдите общий вид первообразных для функции  f(x) =  2 sin 3 x	а) F(x)= - 1/6  cos 3x + С б) F(x)= - 2/3  cos x + С в) F(x)= - 2/3  cos 3x + С
5.     Найдите общий вид первообразных для функции  f(x) =   (2х – 1)5	а) F(x)= (2х – 1)6/12 + С б) F(x)= (2х – 1)6/6 + С в) F(x)= (2х – 1)6/2 + С
6.     Для функции  f(x) найдите F(x), если      f(x) =  2/ х3   ;    F(1)=1	а) F(x)= - х-2 - 2 б) F(x)= - х-2  + 2 в) F(x)= - 2 х-2 + 3
7.     Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции?	а) да б) нет
8.     Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке:	в а) S=∫а f(x)dx                     в б)  S= - ∫а f(x)dx                    в)   S= f(в) - f(а)
9.     Вычислите интеграл          1                                                                   ∫0 4х3dx	а) - 1 б)  4 в)  1
10. По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке:	2 а)   S=∫-1 x2dx                  2 б)  S=∫0 x2dx                  -1  в)  S=∫2 x2dx

 

ВАРИАНТ № 2

Задание	Вариант ответа
1.     Среди заданных функций G(x), F(x) и H(x) выберете первообразную для функции                        у =  5 х6	а) G(x)= 5 х7 б) F(x)=  30 х5 в) H(x)=  5х7/7
2.     Укажите ту функцию, для которой                         F(x)=  х4  - 4х + С       имеет общий вид первообразной	а) g(x)= 4 х3  - 4 + С б) h(x)= 4 х3  - 4 х2 + 2 в) φ(x)=  х5/5  - 2 х2
3.     Найдите общий вид первообразных для функции  f(x) =  5 cos x + 2 sin x	а) F(x)= 5 sin x - 2 cos x + С б) F(x)= - 5 sin x - 2 cos x + С в) F(x)= 5 sin x + 2 cos x + С
4.     Найдите общий вид первообразных для функции  f(x) =   3 cos 2x	а) F(x)= - 3/2 sin 2x + С б) F(x)= 3/2 sin 2x + С в) F(x)=  3/2 sin x + С
5.     Найдите общий вид первообразных для функции  f(x) =    (7х – 2)3	а) F(x)= (7х – 2)4/4 + С б) F(x)= 7(7х – 2)4/4 + С в) F(x)= (7х – 2)4/28 + С
6.     Для функции  f(x) найдите F(x), если       f(x) = 2/ х2     ;      F(1)=1	а) F(x)= 2 х-1 + 1 б) F(x)= -2 х-1  + 3 в) F(x)= 2 х-1 - 1
7.     Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции?	а) да б) нет
8.     Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке:	в а) S = ∫а f(x)dx                         в б)     S = - ∫а f(x)dx                        a в)   S = - ∫в f(x)dx
9.     Вычислите интеграл          0                                                                   ∫-1 5х4dx	а)  5 б)  -1 в)  1
10. По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке:	1 а) S=∫-2 (х2 +2)dx                 -2 б) S=∫1(х2 +2)dx                               2  в)  S=∫-2 (х2 +2)dx

 

ВАРИАНТ № 3

Задание	Вариант ответа
1.     Среди заданных функций G(x), F(x) и H(x) выберете первообразную для функции                               у = -5 х4	а) G(x)= -20 х3 б) F(x)= - х5 в) H(x)=  -  5/4 х5
2.     Укажите ту функцию, для которой       F(x)= х2 - 2x + С        имеет общий вид первообразной	а) g(x)= 2х - 2 б) h(x)= 2 х3 - 2x2 + 2 в) φ(x)=  х3/3 - 2
3.     Найдите общий вид первообразных для функции  f(x) =    6 sin x + 3 cos x	а) F(x)= 6cos x – 3 sin x + С б) F(x)= - 6 cos x + 3 sin x в) F(x)= - 6 cos x + 3 sin x+ С
4.     Найдите общий вид первообразных для функции  f(x) =  5 sin 4 x	а) F(x)=  1/4  cos 5x + С б) F(x)= - 5/4  cos x + С в) F(x)= - 5/4 cos 4x + С
5.     Найдите общий вид первообразных для функции  f(x) =   (1 - 5х)3	а) F(x)= -(1 - 5х)4/20 + С б) F(x)= (1 - 5х)4/4 + С в) F(x)= (1 - 2х)3/3 + С
6.     Для функции  f(x) найдите F(x), если      f(x) =  4/ х5   ;    F(1)=1	а) F(x)= - х-4 - 2 б) F(x)= - х-4  + 2 в) F(x)=  6 х-6 + 3
7.     Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции?	а) да б) нет
8.     Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке:	в а) S=-∫а f(x)dx                    в б)  S=  ∫а f(x)dx                    в)   S= f(а) - f(в)
9.     Вычислите интеграл          1                                                                   ∫0 6х5dx	а)  6 б)  -1 в)   1
10. По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке:	1 а)   S=∫-1 (x2 -1)dx                  1 б)  S=∫0 (x2 -1)dx                  -1  в)  S=∫1 (x2 -1)dx

 

ВАРИАНТ № 4

Задание	Вариант ответа
1.     Среди заданных функций G(x), F(x) и H(x) выберете первообразную для функции                        у =  9 х8	а) G(x)=  х9 б) F(x)=  72 х7 в) H(x)=  9 х7/7
2.     Укажите ту функцию, для которой                         F(x)=  х5  - 5х + С       имеет общий вид первообразной	а) g(x)= 5 х4  - 5 х2 + С б) h(x)= 5 х6  - 5 х2 в) φ(x)=  5х4  - 5
3.     Найдите общий вид первообразных для функции  f(x) =  4 cos x + 7 sin x	а) F(x)= 4 sin x - 7 cos x + С б) F(x)= - 4 sin x - 7 cos x + С в) F(x)= 4 sin x + 7 cos x + С
4.     Найдите общий вид первообразных для функции  f(x) =   9 cos 3x	а) F(x)= - 3 sin 3x + С б) F(x)= 3 sin 3x + С в) F(x)=  3 sin x + С
5.     Найдите общий вид первообразных для функции  f(x) =    (7х – 2)3	а) F(x)= (7х – 2)4/4 + С б) F(x)= 7(7х – 2)4/4 + С в) F(x)= (7х – 2)4/28 + С
6.     Для функции  f(x) найдите F(x), если       f(x) = 5/ х6     ;      F(1)=1	а) F(x)=  х-5 + 1 б) F(x)= - х-5  + 2 в) F(x)= - х-5 - 1
7.     Верно ли, что на рисунке изображены графики трёх первообразных для некоторой функции?	а) да б) нет
8.     Выберете формулу, по которой можно вычислить площадь фигуры, изображённой на рисунке:	в а) S = ∫а f(x)dx                         в б)     S = - ∫а f(x)dx                        a в)   S = - ∫в f(x)dx
9.     Вычислите интеграл          0                                                                     ∫-1 7х6dx	а)  7 б)  -1 в)  1
10.  По какой формуле нужно находить площадь фигуры, заштрихованной на рисунке:	3 а) S=∫0 (х -1)2dx                            3 б) S=∫1(х -1)2dx                               1  в)  S=∫3 (х -1)2dx

 

 

Ключ к тесту

 «ПЕРВООБАЗНАЯ И ИНТЕГРАЛ»:

ВАРИАНТ № 1:    в, а, б, в, а, б, а, а, в, а.

 

ВАРИАНТ № 2:     в, а, а, б, в, б, б, б, в, а.

 

ВАРИАНТ № 3:    б, а, в, в, а, б, б, а, в, а

 

 ВАРИАНТ № 4:   а, в, а, б, в, б, а, а, в, б.   

Проверочная работа  «Иррациональные уравнения» Вариант 1 Решить уравнения: 1.   = 3; 2.   + 1 = 0; 3.   = ; 4.   = 3 – х; 5.   ∙  = х +5.	Проверочная работа  «Иррациональные уравнения» Вариант 2 Решить уравнения: 1.    = 2 ; 2.    -  4 = 0; 3.    = ; 4.    = х - 2; 5.  9 – х = ∙ .
Проверочная работа  «Иррациональные уравнения» Вариант 3 Решить уравнения: 1.    = 3; 2.  1 -  = 0; 3.   = ; 4.  = х - 5; 5.    ∙  = 3х +1.	Проверочная работа  «Иррациональные уравнения» Вариант 4 Решить уравнения: 1.    = 4; 2.   + 1 = 3; 3.    =  ; 4.     = 2х + 1; 5.    ∙  = 2х +9.
Проверочная работа  «Иррациональные уравнения» Вариант 5 Решить уравнения: 1.     = 4; 2.    +  6 = 4; 3.     =  ; 4.    = х - 5; 5.    ∙   = 3х - 1.	Проверочная работа  «Иррациональные уравнения» Вариант 6 Решить уравнения: 1.    = 2; 2.  10 = + 1: 3.    = ; 4.    = х - 8; 5.    ∙  = х + 6.
Проверочная работа  «Иррациональные уравнения» Вариант 7 Решить уравнения: 1.   = 1; 2.   + 7 = 0; 3.    =  ; 4.     = х - 1; 5.    ∙   = х +3.	Проверочная работа  «Иррациональные уравнения» Вариант 8 Решить уравнения: 1.    = 3; 2.    - 3 = 0; 3.    = 4.  х – 2 =  ; 5.    ∙  = 4х + 3.

 

Ответы к вариантам проверочной работы

 «Иррациональные уравнения»

№ варианта	Уравнение 1	Уравнение 2	Уравнение 3	Уравнение 4	Уравнение 5
1	5	Нет решений	2	1	-1; 5
2	5	16	-2; 2	5	-3
3	11	1	3	5	1
4	7	4	-3; 3	1	Нет решений
5	-5; 5	Нет решений	5	8	7
6	11	81	3	11	10
7	2	Нет решений	8	4	5
8	-4; 4	9	3	2	13

 

 

Контрольная работа № 6 «РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ» Вариант 1   1.        = 23-2х;   2.            7х+2 - 14∙7х = 5;   3.            49х - 8∙7х + 7 = 0;   4.        > 92х-1;   5.            10∙5х-1 + 5х+1 < 7.

Контрольная работа № 6 «РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ» Вариант 2   1.           = 1253-4х;   2.                2х+4 - 2х = 120;   3.                36х - 4∙6х - 12 = 0;   4.           <  8х-1;   5.                8∙2х-1 - 2х > 48.

 

 

ОТВЕТЫ к контрольной  работе № 6

«РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ»

 

№ варианта	Задание 1	Задание 2	Задание 3	Задание 4	Задание 5
1		-1	1; 0	х < -4	х < 0
2		3	1	х >	х >4

 

ЗАЧЁТ

«Основные методы решения уравнений, неравенств и систем»

Вариант 1

1. Решить иррациональное уравнение     3х + 1 =  .

2. Решить показательное уравнение    

 

4. Решить логарифмическое неравенство   +

5. Решить тригонометрическое уравнение    + = 0.

 

Вариант 2

1. Решить иррациональное уравнение     8 - 3х =  .

2. Решить показательное неравенство     ≤ 81.

 

 

4. Решить логарифмическое неравенство  + > -3.

5. Решить тригонометрическое уравнение    3 = 2

 

Вариант 3

1. Решить иррациональное уравнение      = 6 + х..

2. Решить показательное уравнение     9^х - 2∙3^х = 63.

4. Решить логарифмическое неравенство 

5. Решить тригонометрическое уравнение    2

 

Вариант 4

1. Решить иррациональное уравнение      = 6 – х.

2. Решить показательное неравенство   

4. Решить логарифмическое уравнение 

 

ОТВЕТЫ к ЗАЧЁТУ

«Основные методы решения уравнений, неравенств и систем»

 

№ варианта   № задания	Вариант 1	Вариант 2	Вариант 3	Вариант 4
1.	0	2	-3	2
2.	2	[-2;2]	2	[0;4]
3.	(1;2)	(1;0)	(	(10;2)
4.	(2;4)	(0;3)	(1,2;12)	8
5.	±+ 2πn, n z; π+ 2πk, k z.	(-1)k + πk, k z	+ πn, n z	+ 2πn, n z

 

 

Контрольная работа № 7

«Аксиомы стереометрии. Параллельность прямых и плоскостей»

Вариант 1

1.   Что такое стереометрия.

2.   Какие прямые в пространстве называются параллельными?

3.   Дана плоскость β и прямые а. в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая а параллельна прямой  с, прямые  в и с пересекаются, а прямая с лежит в плоскости  Сделайте рисунок и прокомментируйте его  с помощью математических знаков.

4.   Через точки  А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А₁, В_1, М₁ соответственно. Найти длину отрезка ММ₁, если АА₁=13м, ВВ₁=7м, причём отрезок АВ не пересекает плоскость α.

5.   Через конец  А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В₁ и С₁. Найдите длину отрезка ВВ₁, если СС₁=21 см, АС : ВС = 3 : 4.

 

 

Вариант 2

1.   Назовите основные фигуры в пространстве.

2.   Какие прямые в пространстве называются скрещивающимися?

3.   Дана плоскость β и прямые а, в и с. Известно, что одна из данных прямых параллельна плоскости β. Назовите эту прямую, если прямая в параллельна прямой  с, прямые  а и в пересекаются, а прямая с лежит в плоскости  Сделайте рисунок и прокомментируйте его  с помощью математических знаков.

4.   Через точки  А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А₁, В_1, М₁ соответственно. Найти длину отрезка ММ₁, если АА₁=3м, ВВ₁=17м, причём отрезок АВ не пересекает плоскость α.

5.   Через конец  А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В₁ и С₁. Найдите длину отрезка ВВ₁, если

СС₁=26 см, АВ : АС = 15 : 13.

 

 

Вариант 3

1.       Сформулируйте теорему о трёх точках?

2.       Что значит: прямая и плоскость параллельны?

3.       Дана плоскость β и прямые  а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежит в плоскости β, прямая в параллельна плоскости β, а прямая с пересекает плоскость  β. Сделайте рисунок и прокомментируйте его  с помощью математических знаков.

4.       Через концы   отрезка  АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А₁, В₁ и М₁. Найти длину отрезка ММ₁, если отрезок АВ не пересекает плоскость α и если АА₁=10м, ВВ₁=14м.

5.       Через конец  А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В₁ и С₁. Найдите длину отрезка ВВ₁, если

АВ=8 см, АС : СС₁ = 2 : 3.

 

 

Вариант 4

1.       Сформулируйте теорему о прямой и точке.

2.       Какие плоскости  называются параллельными?

3.       Дана плоскость β и прямые  а, в и с, причём две из трёх данных прямых параллельны. Назовите параллельные прямые, если прямая а лежит в плоскости β, а прямые  в и с пересекают плоскость  β. Сделайте рисунок и прокомментируйте его  с помощью математических знаков.

4.       Через концы   отрезка  АВ и его середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А₁, В₁ и М₁. Найти длину отрезка ММ₁, если отрезок АВ не пересекает плоскость α и если АА₁=12м, ВВ₁=8м.

5.       Через конец  А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые В₁ и С₁. Найдите длину отрезка ВВ₁, если

СС₁=14 см, АВ : ВС = 10 : 3.

 

Ответы к контрольной работе № 7

«Аксиомы стереометрии. Параллельность прямых и плоскостей»

	Вариант 1	Вариант 2	Вариант 3	Вариант 4
1	Стереометрия – это раздел геометрии, в ко-тором изучаются фигу-ры в пространстве.	Основными фигурами в пространстве являются точка, прямая и плос-кость.	Через три точки, не ле-жащие на одной пря-мой, можно провести плоскость, и притом только одну.	Через прямую и не ле-жащую на ней точку можно провести плос-кость, и при том только одну.
2	Две прямые в пространс-тве называются парал-лельными, если они ле-жат в одной плоскости и не пересекаются.	Прямые, которые не пе-ресекаются и не лежат в одной плоскости, назы-ваются скрещивающи-мися.	Прямая и плоскость параллельны – значит, они не пересекаются, то есть не имеют общих точек.	Две плоскости называ-ются параллельными, если они не пересека-ются, то есть не имеют общих точек.
3	а   ;;;	в                ; ;;	аив;   ;;;	вис    ;;
4	АВВ1А1 –тра- пеция, т.к. ММ1- средняя линия;	АВВ1А1 –тра- пеция, т.к. ММ1- средняя линия;	АВВ1А1 –тра- пеция, т.к. ММ1- средняя линия;	АВВ1А1 –тра- пеция, т.к. ММ1- средняя линия;
5	∆АВВ1∞ ∆АСС1	∆АВВ1∞ ∆АСС1	∆АВВ1∞ ∆АСС1	∆АВВ1∞ ∆АСС1

 

Контрольная работа № 8     «МНОГОГРАННИКИ»

Вариант 1

1.     Дайте определение прямой призмы.

2.     Что такое параллелепипед?

3.     Что такое многогранник?

4.     Задача: У параллелепипеда три грани имеют площади 2 м², 4 м²  и 5 м². Чему равна полная поверхность параллелепипеда?

5.     Задача: Основание пирамиды – прямоугольник со сторонами 9 и 12 см, все боковые рёбра равны 12,5 м. Найдите объём пирамиды.

 

Вариант 2

1.     Дайте определение правильной призмы.

2.     Что такое куб?

3.     Чем является точка пересечения диагоналей параллелепипеда?

4.     Задача: У параллелепипеда три грани имеют площади 3 м², 6 м²  и 7 м². Чему равна полная поверхность параллелепипеда?

5.     Задача: Боковые рёбра наклонной треугольной призмы равны 15 м, а расстояния между содержащими их параллельными прямыми 26 м, 25 м и 17 м. Найдите объём призмы.

 

Вариант 3

1.     Дайте определение правильной пирамиды.

2.     Какой многогранник называется правильным?

3.     Что такое линейные размеры прямоугольного параллелепипеда?

4.     Задача: Измерения прямоугольного параллелепипеда 15 м, 50 м и 36 м. Найдите ребро равновеликого ему куба.

5.     Задача:  Высота правильной четырёхугольной пирамиды равна 7 см, а сторона основания 8 см. Найдите боковое ребро.

 

 

Вариант 4

1.     Дайте определение апофемы правильной пирамиды.

2.     Какой параллелепипед называется прямоугольным?

3.     Чему равна боковая поверхность прямой призмы?

4.     Задача: Найдите диагонали прямоугольного параллелепипеда по трём его измерениям: 2 см, 3 см, 6 см.

5.     Задача: Основание пирамиды – прямоугольник со сторонами  6 см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислите высоту пирамиды.

 

 

Ответы к контрольной работе № 8 «Многогранники»

№ варианта №  задания	Вариант 1	Вариант 2	Вариант 3	Вариант 4
1.	Призма называется прямой, если её боковые рёбра перпендикулярны основаниям.	Прямая призма на-зывается правиль-ной, если её основа-ния являются пра-вильными много-угольниками.	Пирамида называ-ется правильной, если её основанием является правиль-ный многоуголь-ник, а основание высоты совпадает с центром этого мно-гоугольника.	Высота боковой грани правильной пирамиды, прове-дённая из её верши-ны, называется апофемой.
2.	Если основания призмы есть параллелограмм, то она называется параллелепипедом.	Прямоугольный параллелепипед, у которого все рёбра равны, называется кубом.	Выпуклый много-гранник называет-ся правильным, ес-ли его грани явля-ются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число рёбер.	Прямой параллеле-пипед, у которого основанием является прямоугольник, на-зывается прямоугольным параллелепипедом.
3.	Многогранник – это такое тело, поверх-ность которого сос-тоит из конечного числа плоских мно-гоугольников.	Точка пересечения диагоналей паралле-лепипеда является его центром сим-метрии.	Длины непарал-лельных рёбер пря-моугольного па-раллелепипеда на-зывают его линей-ными размерами.	Боковая поверх-ность прямой приз-мы равна произведе-нию периметра ос-нования на высоту призмы, т.е. на дли-ну бокового ребра.
4.	Sn=2(2+4+5)= =22 см2.	Sn=2(3+6+7)= =32 см2.	Vn= Vк Vn=abc=15∙50∙36 Vк=a3	d2=a2+ b2+ c2= =22+ 32+ 62=49  d=7 (см)
5.	H  Sосн. = =9•12= = 108см2 BD=   == =15(см) ОD= BD=7, 5 см SO== === =10(см) = =360 (см3).	V=Sосн.∙l Sосн.=   ; Sосн.= .=  =204; V=204∙15=3060(см3)	ОD= BD=4	SO=h AC=BD= == =10 (см)  ОD= BD= 5 см SO== = =  = = 12 см.

 

Контрольная работа № 9 «ТЕЛА ВРАЩЕНИЯ»

Вариант 1

6.     Дайте определение цилиндра. Нарисуйте цилиндр, укажите его образующую, радиус и осевое сечение.

7.     Какой конус называется прямым? Сделать рисунок.

8.     Какая плоскость называется диаметральной плоскостью шара? Что такое большой круг? Сделать рисунок.

9.     Задача: Куча щебня имеет коническую форму, радиус основания которой 4 м, а образующая 5 м. Найдите объём щебня.

10. Задача: Найти площадь сечения шара радиусом 25 см плоскостью, проведённой на расстоянии  20 см от центра шара.

 

Вариант 2

1.     Дайте определение конуса. Нарисуйте конус, укажите его образующую, радиус, высоту и осевое сечение.

2.     Какой цилиндр называется прямым? Сделать рисунок.

3.     Какая плоскость называется касательной к шару? Сделать рисунок.

4.   Задача: Объём шара равен  см³. Найдите площадь поверхности шара.

5.   Задача: Площадь боковой поверхности конуса равна 15 см², а площадь его основания на 6 см² меньше. Найдите объём конуса.

 

Вариант 3

1.     Дайте определение шара. Нарисуйте шар, укажите его центр, радиус.

2.     Укажите виды сечений цилиндра и  сделайте рисунки.

3.     Какая фигура получится при вращении равнобедренного треугольника вокруг его оси симметрии? Сделайте рисунок.

4.     Задача: Радиус цилиндра равен 5 см, площадь боковой поверхности вдвое больше площади основания. Найдите объём цилиндра.

5.     Задача: Плоскость проходит на расстоянии 6 см от центра шара. Радиус сечения равен 8 см. Найдите площадь поверхности шара.

 

Вариант 4

1.     Почему шар является телом вращения. Сделайте рисунок. Дайте определение сферы.

2.     Что такое усечённый конус? Сделать рисунок.

3.     Какая фигура получится при вращении прямоугольника вокруг его оси симметрии? Сделайте рисунок.

4.     Задача: Площадь осевого сечения цилиндра равна 64 см². Найдите площадь его боковой поверхности.

5.     Задача: Найти объём тела, полученного при вращении прямоугольного треугольника с гипотенузой 24 см и острым углом вокруг меньшего катета.

 

Ответы к контрольной работе № 9 «Тела вращения»

№ варианта №  задания	Вариант 1	Вариант 2	Вариант 3	Вариант 4
6.	Цилиндром называется тело, которое состоит из двух кругов (оснований), не лежащих в одной плос-кости и совмещаемых параллельным переносом, и всех отрезков (образующих), соединяю-щих соответствующие точки этих кругов.	Конусом называется тело, которое состо-ит из круга –основа- ния конуса, точки, не лежащей в плос-кости этого круга,- вершины конуса и всех отрезков (обра-зующих), соединяю-щих вершину конуса с точками основания	Шаром называется тело, которое состоит из всех точек пространства, на-ходящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара.	Шар получается при вра-щении полукруга вокруг его диаметра как оси.   Граница шара называется сферой.
7.	Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.	Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.	Осевое сечение   сечения параллельные оси и плоскости основания	Плоскость, параллельная основанию конуса и пересекающая конус, отсекает   от него меньший конус. Оставшаяся часть называется усечённым конусом.
8.	Плоскость, проходящая через центр шара, называется диаметральной.	Плоскость,    проходящая через точ-ку  А шаровой поверх-ности и перпендику-лярная радиусу, прове-дённому в точку А, на-зывается касательной плоскостью.	конус	цилиндр
9.		Sп= 4πR2	V=Sосн.∙Н= πR2H     Sбок.= 2Sосн    2πRH= 2πR2;  R=H    V= π52∙5=125π см3	Sос.сеч.=2RH Sбок.=2πRH= = Sос.сеч.π = 64π см2
10.	Sсеч= πr2 r2 =R2-d2= 625-400=225 Sсеч= 225π см2		Sп= 4πR2 Sп= 4π102=400 π см2	H=l =1728 π см3

 

 

Тесты по теме: «Аксиомы стереометрии и их простейшие следствия. Параллельность прямых и плоскостей»

ВАРИАНТ № 1

Задание	Вариант ответа
1.     Продолжи предложение: Стереометрия – это раздел геометрии, в котором изучаются фигуры….	а) на плоскости; б) в пространстве; в) на прямой.
2. Какие прямые в пространстве называются параллельными?	а) если ни лежат в одной плоскости и не пересекаются; б) если они лежат в одной плоскости и пересекаются; в) если они лежат в разных плоскостях и не пересекаются.
3. На рис.1 скрещивающимися являются прямые:	а)  АВ и ВВ1; б) АВ и Д1С1; в) АВ и А1Д1.
4. Записать, используя математическую символику: Плоскость α пересекает плоскость β по прямой а.	а) α β=а; б) α∩β=а; в) α Є β=а.
5. Как прочесть запись: [АВ]  а;  а Є α  ?	а) отрезок АВ принадлежит прямой а, не лежащей в плоскости α; б) отрезок АВ лежит на прямой а, не принадлежащей плоскости α; в) точки  А и В лежат на  прямой а, не принадлежащей  плоскости α;
6. Точки А, В, С и Д  не лежат в одной плоскости	а) прямые АВ и СД пересекаются; б) прямые АВ и СД не пересекаются.
7. Прямые АВ и СД не лежат в одной плоскости	а) прямые  АС и ВД не лежат в одной плоскости; б) прямые  АС и ВД лежат в одной плоскости;
8. Может ли при параллельном проектировании параллелограмма получиться трапеция?	а) может, так как при параллельном проектировании параллельность не сохраняется; б) не может, так как при параллельном проектировании параллельность  сохраняется.
9. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти отрезок М1М1, если А А1=3м; ВВ1=17м, причем АВ не пересекает плоскость α.	а) М1М1=10 м; б) М1М1=62/3 м; в) М1М1=20м.
10.Дано: ∆АВС; α||АВ; АС∩ α= А1; ВС∩ α= В1; АВ=15 см; АА1: АС=2:3. Найти А1В1 -?	а) А1В1=45 см; б) А1В1= 5 см; в) А1В1=10 см.

 

 

ВАРИАНТ № 2

Задание	Вариант ответа
2.     Продолжи предложение: Основными фигурами в пространстве являются….	а) точка и прямая; б) точка и плоскость; в) точка, прямая и плоскость.
2. Какие прямые называются скрещивающимися?	а) прямые, которые не  пересекаются и не лежат в одной плоскости; б) прямые, которые   пересекаются и  лежат в одной плоскости; в) прямые, которые не  пересекаются и лежат в одной плоскости.
3. На рис.1 параллельными являются прямые:	а)  А1А и ВС; б) А1 Д1 и ВС; в) А1 В1 и ВС1.
4. Записать, используя математическую символику: Прямая а пересекает плоскость α в точке А.	а) а α=А; б) а α=А; в) а∩α=А.
5. Как прочесть запись: {А;В} Є а;  а  α  ?	а) отрезок АВ принадлежит прямой а, лежащей в плоскости α; б) точки  А и В принадлежат  прямой  а, которая лежит в плоскости α; в) точки  А и В лежат на  прямой а, не принадлежащей  плоскости α;
6. Могут ли прямые а и в пересекаться?  с||в.	а) нет; б) могут.
7. Четыре точки не лежат в одной плоскости. Могут ли какие-нибудь три из них лежать на одной прямой?	а)могут; б) не могут.
8. Может ли проекция параллелограмма при параллельном проектировании быть квадратом?	а) может, так как при параллельном проектировании параллельность  сохраняется; б) не может, так как при параллельном проектировании параллельность не сохраняется.
9. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти отрезок М1М1, если А А1=13м; ВВ1=7м, причем АВ не пересекает плоскость α.	а) М1М1=21/7  м; б) М1М1=20 м; в) М1М1=10м.
10.Дано: ∆АВС; α||АВ; АС∩ α= А1; ВС∩ α= В1; АВ=8 см; АА1: АС=5:3. Найти А1В1 -?	а) А1В1=1 см; б) А1В1= 3 см; в) А1В1=4 см.

 

ВАРИАНТ № 3

Задание	Вариант ответа
3.     Продолжи предложение: В стереометрии свойства геометрических фигур устанавливаются путём доказательства соответствующих….	а) аксиом; б) теорем; в) задач.
2. Что значит: прямая и плоскость параллельны?	а) прямая и плоскость  не  пересекаются; б) прямая и плоскость  пересекаются и  лежат в одной плоскости; в) прямая и плоскость не  пересекаются, то есть не имеют общих точек.
3. На рис.1 скрещивающимися являются прямые:	а)  А1А и ВС; б) А1 Д1 и ВС; в) А1 В1 и АВ.
4. Записать, используя математическую символику: Плоскость α пересекает плоскость β по прямой с.	а) α β =с; б) α  β =с; в) α ∩ β =с.
5. Как прочесть запись: [ВС]  Є с;  с  α  ?	а) отрезок ВС принадлежит прямой с, лежащей в плоскости α; б) точки  С и В принадлежат  прямой  с, которая лежит в плоскости α; в) точки  А и В лежат на  прямой с, не принадлежащей  плоскости α;
6. Точки К, L, M и N  не лежат в одной плоскости	а) прямые KL и MN пересекаются; б) прямые KL и MN не пересекаются.
7.Плоскости α и β параллельны плоскости γ. Могут ли плоскости α и  β  пересекаться?	а) могут; б) не могут.
8.Дана параллельная проекция треугольника. Чем изображается проекция средней линии треугольника?	а) средней линией, так как при параллельном проектировании   сохраняется отношение отрезков; б) средней линией, так как при параллельном проектировании   не сохраняется отношение отрезков .
9. Через точки А, В и середину М отрезка АВ проведены параллельные прямые, пересекающие некоторую плоскость α в точках А1, В1, М1 соответственно. Найти отрезок М1М1, если А А1=25дм; ВВ1=5дм, причем АВ не пересекает плоскость α.	а) М1М1=5  дм; б) М1М1=30 дм; в) М1М1=15 дм.
10.Дано: ∆АВС; α||АВ; АС∩ α= А1; ВС∩ α= В1; АВ=24 см; АА1: АС=5:1. Найти А1В1 -?	а) А1В1=6 см; б) А1В1= 3 см; в) А1В1=4 см.

 

Ключ к тесту

по теме:

«Аксиомы стереометрии и их простейшие следствия. Параллельность прямых и плоскостей»:

ВАРИАНТ № 1:    б, а, в, б, б, б, а, б, а, б

ВАРИАНТ № 2:     в, а, б, в, б, а, б, а, в, б.

ВАРИАНТ № 3:    б, в, а, в, а, б, б, а, в, в.

 

Математический диктант «ВЕКТОРЫ В ПРОСТРАНСТВЕ»

(на 10 – 15 минут)

Вариант № 1

1.     Что называется вектором в пространстве?

2.     Дайте определение действий над векторами: скалярного произведения.

3.     Дайте определение координат вектора с началом в точке А₁(х₁; у₁; z₁) и концом в точке А₂(х₂; у₂; z₂).

4.     Какие вектора называются равными.

5.     Какие вектора называются противоположно направленными?

 

 

Вариант № 2

1.     Какие вектора называются коллиниарными?

2.     Что такое абсолютная величина вектора?

3.     Какие вектора называются одинаково направленными?

4.     Дайте определение действий над векторами: сложения и умножения.

5.     Что такое нулевой вектор?

 

 

ОТВЕТЫ

 на математический диктант

«ВЕКТОРЫ В ПРОСТРАНСТВЕ»

 

№  варианта    № задания	Вариант № 1	Вариант № 2
1.	Вектором в пространстве называется направленный отрезок.	Два ненулевых вектора называются коллиниарными, если они лежат на одной прямой или на параллельных прямых.
2.	Скалярным произведением векторов  называется число а1в1+ а2в2+ а3в3.   ∙=∙.	Абсолютной величиной вектора .
3.	Координатами вектора с началом в точке А1(х1; у1; z1) и концом в точке А2(х2; у2; z2) называются числа х2 - х1; у2 - у1; z2 - z1.	называются одинаково направленными, если полупрямые АВ и СD одинаково направлены.
4.	Вектора называются равными, если они сонаправлены и их длины равны (если они совмещаются параллельным переносом). У равных векторов соответствующие координаты равны.	Суммой векторов  а1;а2;а3)  и 1;2;3) называют вектор 1;2;3). Произведением вектора   (а1; а2; а3) на число λ называется вектор λ= Если λ>0,то направление совпадает с направлением вектора  ; если λ<0, то направление противоположно направлению вектора  .
5.	называются противоположно направленными, если полупрямые АВ и СD противоположно направлены.	Любая точка в пространстве может рассматриваться как вектор. Такой вектор называется нулевым.

 

 Контрольная работа № 10

«Декартовы координаты и векторы в пространстве»

Вариант № 1

1. Сторона равностороннего треугольника равна 12 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью .

2. Даны точки А(0;0;7), В(1;4;2), С(0;4;5), D(4;2;0). Какие из этих точек лежат:

1) в плоскости  ху; 2) на оси z; 3) в плоскости уz.

3. Докажите, что четырёхугольник АВСD с вершинами в точках А(0;2;-3),

В(-1;1;1), С(2;-2;-1), D(3;-1;-5).

    

     5.  Даны точки А(1;-1;3), В(3;-1;1) и С(-1;1;3). Вычислите угол между векторами

          .

 

 

Вариант № 2

1.      Дан прямоугольный треугольник с катетами 6 и 9 см. Найти площадь его ортогональной проекции на плоскость, которая образует с плоскостью .

2.     Даны точки А(0;6;0), В(0;3;3), С(3;4;8), D(1;0;9). Какие из этих точек лежат:

1) в плоскости  хz; 2) на оси у; 3) в плоскости уz.

3.  Докажите, что четырёхугольник АВСD с вершинами в точках А(2;1;3),

В(1;0;7), С(-2;1;5), D(-1;2;1).

    

      5.  Даны точки А(1;3;0), В(2;3;-1) и С(1;2;-1). Вычислите угол между векторами

          .

 

ОТВЕТЫ   к   контрольной работе

«Декартовы координаты и векторы в пространстве»

 

№  варианта    № задания	Вариант № 1	Вариант № 2
6.	= = ===54(см2)	= = 27 = 13,5(см2)
7.	1) в ху:  D; 2) на оси z: А; 3) в уz: А; С.	1) в хz:  D; 2) на оси у: А; 3) в уz: А; В.
8.	Воспользуемся формулами для координат середины отрезка в пространстве. АС: х=  у= z= ВD: х= у= z= Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.	Воспользуемся формулами для координат середины отрезка в пространстве. АС: х= у= z= ВD: х= у= z= Координаты середины отрезков АС и ВD совпадают, поэтому диагонали АС и ВD четырёхугольника АВСD пересекаются и точкой пересечения делятся пополам, следовательно четырёхугольник АВСD – параллелограмм.
9.	5 – 3 = 2; 1 – (-1) = 2; 1 - 2 = -1.	3 – 5 = -2; -1 – 1 = -2; 2 – 1 = 1.
10.	3-1 = 2; -1 – (-1) = 0; 1 – 3 = -2.  3 – (-1) = 4; -1 – 1 = -2; 1 – 3 = -2.	1 – 1 = 0; 3 – 2 = 1; 0 – (-1) = 1.  1 – 2 = -1; 3 – 2 = 1; -1 – (-1) = 0.

 

 

 Контрольная работа № 11

Решение уравнений по определению логарифма

Вариант 1

Пример 1. Решите уравнение =.

Пример 2. Найдите корень уравнения .

 

Пример 3. Решите уравнение 

Пример 4. Найдите корень уравнения .

          Пример 5. Решите уравнение .

 

Вариант 2

Пример 1. Решите уравнение 

 

Пример 2. Найдите корень уравнения .

 

Пример 3. Найдите корень уравнения .

 

Пример 4. Найдите корень уравнения .

 

Пример 5. Решите уравнение .

 

Ответы к контрольной работе № 11

Решение уравнений по определению логарифма

Вариант 1

Решение 1 Это уравнение определено для тех значений х, при которых выполняются неравенства 2х+3>0 и х+1>0.

Для этих х данное уравнение равносильно уравнению 2х+3=х+1. Отсюда х= ‑ 2.  Число – 2 не удовлетворяет неравенству х+1>0, следовательно, данное уравнение не имеет решений.

Ответ: нет решений

Решение 2. Последовательно получаем:     . Число 10 входит в область определения (10 – 4=6>0), значит, является корнем уравнения.

Ответ: 10

 

Решение 3.       .

Выполнив проверку, убеждаемся, что 3 является корнем уравнения.

Ответ: 3

Решение 4. Перенесем  в правую часть уравнения. Получим уравнение, равносильное данному: . Отсюда     .

Делаем проверку: 9‑ 7=2>0, 11 – 9=2>0. Значит, число 9 является корнем уравнения.

Ответ: 9

Решение 5. По определению логарифма ;

; .

Ответ: 8

 

Вариант 2

Решение 1. По определению логарифма имеем . Отсюда х=3.

Число 3 входит в область определения, следовательно, является корнем данного уравнения.

Ответ: 3

 

Решение 2. По определению логарифма получаем:     . Число 82 входит в область определения (82 – 1>0), следовательно, является корнем уравнения.

Ответ: 82

 

Решение 3. Последовательно получаем:         . Число 28 входит в область определения (28 – 1=27>0), значит, является решением уравнения.

Ответ: 28

 

Решение 4. По определению логарифма получаем:     . Число 52 входит в область определения (82 – 1>0), следовательно, является корнем уравнения.

Ответ: 52

Решение 5. По определению логарифма имеем .

. D=16, x₁=3, x₂= ‑ 1.

Оба корня удовлетворяют исходному уравнению.

Ответ: 3; ‑ 1

                                     

Контрольная работа № 12

Задачи по комбинаторике

 

Вариант № 1

Задача 1. У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?

Задача 2. Предприятие может предоставить работу по одной специальности 4 женщинами, по другой - 6 мужчинам, по третьей - 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов: 6 женщин и 8 мужчин?

Задача 3. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человека, при условии, что все они должны ехать в различных вагонах?

Задача 4. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

Задача 5. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую — 5 и в третью — 12. Сколькими способами это можно сделать.

Ответы № 1

  Решение 1. Имеем набор {я, я, г, г, г}. Всего перестановок пятиэлементного множества 5!, но мы не должны учитывать перестановки, в которых объекты одного типа меняются местами несколько раз, поэтому нужно поделить на возможное число таких перестановок: 2! · 3!. Получаем в итоге 5! 2! · 3! = 3 · 4 · 5 2 · 3 = 10. Ответ: 10 способов

  Решение 2. Имеем 14 претендентов и 13 рабочих мест. Сначала выберем работников на первую специальность, то есть 4 женщин из 6: C4 6 = 6! 4! · 2! = 15. Далее независимо аналогичным образом выберем мужчин на вторую специальность: C6 8 = 8! 6! · 2! = 28. Осталось 2 женщины, 2 мужчин и 3 вакантных места, которые, по условию, могут занять любые из четырех оставшихся человек. Это может быть сделано 2 вариантами: 1. 1 женщина и 2 мужчин (выбираем женщину C1 2 = 2 способами) 2. 1 мужчина и 2 женщины (выбираем мужчину C1 2 = 2 способами). В итого получаем 15 · 28(2 + 2) = 1680 способов. Ответ: 1680 способов.

  Решение 3. Т.к. все пассажиры должны ехать в разных вагонах, требуется отобрать 4 вагона из 9 с учетом порядка (вагоны отличаются №), эти выборки – размещения из n различных элементов по m элементов, где n=9, m=4. Число таких размещений находим по формуле: A = n ⋅(n − ⋅()1 n − ⋅...)2 ⋅(n − m + )1 m n . Получаем: 9 8 7 6 3024 4 A9 = ⋅⋅⋅ = . ОТВЕТ. 3024 способами можно рассадить в поезде 4 человек

 Решение 4. Не менее 2-х человек, т.е 2+7 или 3+6 или 4+5 человек (5+4, 6+3, 7+2 – те же самые комбинации). В каждой выборке важен только состав, т.к. члены подгруппы не различаются по ролям, т.е. выборки − сочетания из n различных элементов по m элементов, их число: (! !) ! m n m n C m n ⋅ − = , где n!= 1⋅ 2 ⋅3⋅...⋅ n . Число выборок из 2-х человек: 36 1 2 8 9 !7!2 !9 9(!2 !)2 2 !9 9 = ⋅ ⋅ = ⋅ = ⋅ − C = . Число выборок из 3-х человек: 84 1 2 3 7 8 9 !6!3 !9 9(!3 !)3 3 !9 9 = ⋅⋅ ⋅ ⋅ = ⋅ = ⋅ − C = . Число выборок из 4-х человек: 126 1 2 3 4 6 7 8 9 !5!4 !9 9(!4 !)4 4 !9 9 = ⋅⋅⋅ ⋅ ⋅ ⋅ = ⋅ = ⋅ − C = . Применяем правило сложения: 36 84 126 246 4 9 3 9 2 C9 + C + C = + + = способов ОТВЕТ. 246 способов.

  Решение 5. Создавая первую бригаду, отбирают 3 человека из 20, создавая вторую – 5 из оставшихся 17, создавая третью – 12 из оставшихся 12. Для выборок важен только состав (роли членов бригады не различаются). Эти выборки - сочетания из n различных элементов по m элементов, их число: (! !) ! m n m n C m n ⋅ − = . Создавая сложную выборку (из 3-х бригад), воспользуемся правилом умножения: 3 5 12 20 17 12 20! 17! 12! 20! 17! 12! 3! (20 3)! 5! (17 5)! 12! (12 12)! 3! 17! 5! 12! 12! 0! 13 14 15 16 17 18 19 20 7054320. 1 2 3 1 2 3 4 5 N C= ⋅ ⋅ = ⋅ ⋅ = ⋅ ⋅ = С С ⋅ − ⋅ − ⋅ − ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ = = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ОТВЕТ. 7054320 способов.

Вариант № 2

   ЗАДАЧА 1. Для участия в команде тренер отбирает 5 мальчиков из 10. Сколькими способами он может сформировать команду, если 2 определенных мальчика должны войти в команду?  

 ЗАДАЧА 2. В шахматном турнире принимали участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего партий было сыграно в этом турнире?   

   ЗАДАЧА 3. Сколько различных дробей можно составить из чисел 3, 5, 7, 11, 13, 17 так, чтобы в каждую дробь входили 2 различных числа? Сколько среди них будет правильных дробей?    

 ЗАДАЧА 4. Сколько слов можно получить, переставляя буквы в слове Гора и Институт?  

  ЗАДАЧА 5. Каких чисел от 1 до 1 000 000 больше: тех, в записи которых встречается единица, или тех, в которых она не встречается? РЕШЕНИЕ5. Подсчитаем количество чисел от 1 до 999999 (число 1 000 000 содержит единицу, его сразу отбросим), в записи которых нет единиц. Каждую цифру можно выбрать 9 способами (любая цифра кроме 1), поэтому все 6 цифр (по правилу произведения) можно выбрать 6 9 способами (если в числе до значащих цифр стоят нули, мы их просто отбрасываем). При этом один вариант (000000) нужно убрать, так как число 0 не рассматривается. Получаем всего 6 N = − = 9 1 531440 чисел. Так как всего чисел 1 000 000, то видно, что чисел без единицы среди чисел от 1 до 1 000 000 больше, чем тех, в записи которых единица есть.. __

 

Ответы вариант № 2

 

РЕШЕНИЕ 1. Т.к. известно, что двое мальчиков войдут в команду, то остается отобрать 3 из 8. Для выборки важен только состав (по условию все члены команды не различаются по ролям). Следовательно, выборки – сочетания из n различных элементов по m элементов, их число: (! !) ! m n m n C m n ⋅ − = , где n!= 1⋅ 2 ⋅3⋅...⋅ n , при n=8, m=3. 56 1 2 3 6 7 8 !5!3 !8 8(!3 !)3 3 !8 8 = ⋅⋅ ⋅ ⋅ = ⋅ = ⋅ − C = . ОТВЕТ. 56 способов сформировать команду

РЕШЕНИЕ 2. Способ 1. В одной игре участвуют 2 человека, следовательно, нужно вычислить, сколькими способами можно отобрать 2-х человек из 15, причем порядок в таких парах не важен. Воспользуемся формулой для нахождения числа сочетаний (выборок, отличающихся только составом) из n различных элементов по m элементов (! !) ! m n m n C m n ⋅ − = , где n!= 1⋅ 2 ⋅3⋅...⋅ n , при n=15, m=2. 105 1 2 14 15 !13!2 !15 15(!2 !)2 2 !15 15 = ⋅ ⋅ = ⋅ = ⋅ − C = . В процессе решения исключили 13! из15!, т.е. сократили произведение !15 = 1⋅ 2 ⋅3⋅...⋅15 на !13 = 1⋅ 2 ⋅ 3⋅...⋅13, остались после сокращения множители 14 и 15). Способ 2. Первый игрок сыграл 14 партий (с2-м, 3-м, 4-м, и так до 15-го), 2- ой игрок сыграл 13 партий (3-м, 4-м, и т.д. до 15-го, исключаем то, что с первым партия уже была), 3-ий игрок − 12 партий, 4-ый − 11 партий, 5 – 10 партий, 6 – 9 партий, 7 – 8 партий, 8 – 7 партий, 9 – 6 10 – 5 11 – 4 12 – 3 13 – 2 14 – 1, а 15-ый уже играл со всеми. Итого: 14+13+12+11+10+9+8+7+6+5+4+3+2+1=105 партий ОТВЕТ. 105 партий. __ РЕШЕНИЕ 3. Различных дробей из 6 чисел: 3, 5, 7, 11, 13, 17 можно составить 2 6 6! 2 2 5 6 30 4!2! C ⋅ = ⋅ = ⋅ = штук ( 2 C6 способами выбираем два числа из 6, и двумя способами составляем из них дробь: сначала одно число – числитель, другое знаменатель и наоборот). Из этих 30 дробей ровно 15 будут правильные (т.е., когда числитель меньше знаменателя): 2 6 C =15 способами выбираем два числа из 6, и единственным образом составляем дробь так, чтобы числитель был меньше знаменателя. ОТВЕТ. 30; 15. _ 

РЕШЕНИЕ 4. 1) В слове «гора» четыре буквы, все они различны, поэтому можно получить всего 1 N = = ⋅ ⋅ ⋅ = 4! 1 2 3 4 24 различных слова. 2) В слове «институт» 8 букв, из них две буквы «и», три буквы «т» и по одной букве «н», «с» и «у». Поэтому всего можно получить перестановками букв 2 8! 1 2 3 4 5 6 7 8 3 4 5 7 8 3360 2!3!1!1!1! 1 2 1 2 3 1 1 1 N ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ = = = ⋅ ⋅ ⋅ ⋅ = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ различных слов. ОТВЕТ. 24 и 3360 слов

РЕШЕНИЕ 5. Подсчитаем количество чисел от 1 до 999999 (число 1 000 000 содержит единицу, его сразу отбросим), в записи которых нет единиц. Каждую цифру можно выбрать 9 способами (любая цифра кроме 1), поэтому все 6 цифр (по правилу произведения) можно выбрать 6 9 способами (если в числе до значащих цифр стоят нули, мы их просто отбрасываем). При этом один вариант (000000) нужно убрать, так как число 0 не рассматривается. Получаем всего 6 N = − = 9 1 531440 чисел. Так как всего чисел 1 000 000, то видно, что чисел без единицы среди чисел от 1 до 1 000 000 больше, чем тех, в записи которых единица есть.

 

Контрольная работа № 13

Решения задач на  определение вероятности

 

 Задача 1: Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места.

 Задача 2: Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.

Задача 3. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые.

Задача 4: На шахматную доску случайным образом поставлены две ладьи. Какова вероятность, что они не будут бить одна другую?

Задача 5. Шесть рукописей случайно раскладывают по пяти папкам. Какова вероятность того, что ровно одна папка останется пустой?

 

  

Вариант 2

Задача  1. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное.

Задача  2. На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.

Задача 3. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: "а", "м", "р", "т", "ю". Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово "юрта". 

Задача 4. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?

Задача 5. Пятитомное собрание сочинений расположено на полке в случайном   порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации томов (от 1 до 5)?

 

 

 

Ответы

                  Вариант № 1

 Решение 1: Вероятность набрать верную цифру из десяти равна по условию 1/10. Рассмотрим следующие случаи:
1. первый звонок оказался верным, вероятность равна 1/10 (сразу набрана нужная цифра).
2. первый звонок оказался неверным, а второй - верным, вероятность равна 9/10*1/9=1/10 (первый раз набрана неверная цифра, а второй раз верная из оставшихся девяти цифр).
3. первый и второй звонки оказались неверными, а третий - верным, вероятность равна 9/10*8/9*1/8=1/10 (аналогично пункту 2).

Всего получаем P=1/10+1/10+1/10=3/10=0,3P=1/10+1/10+1/10=3/10=0,3 - вероятность того, что ему придется звонить не более чем в три места.

Ответ: 0,3

Решение 2: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.
m=1m=1, так как только одно число правильное. Подсчитаем количество всех возможных двузначных чисел с разными цифрами, меньшее 30, которые может набрать абонент:

Таких чисел n=18n=18 штук. Тогда искомая вероятность P=1/18P=1/18.

Ответ: 1/18.

Решение 3: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

m=6m=6, так как есть только три случая расположения 6 шаров по 3 ящикам, чтобы во всех ящиках оказалось разное число шаров: (1, 2, 3), (2, 1, 3), (3, 2, 1), (1, 3, 2), (2, 3, 1), (3, 1, 2).

Всего случаев расположения 6 шаров по 3 ящикам, чтобы ни один ящик не остался пустым равно

m=C3−16−1=C25=5!2!3!=4⋅51⋅2=10.m=C6−13−1=C52=5!2!3!=4⋅51⋅2=10.

Тогда искомая вероятность P=6/10=0,6P=6/10=0,6.

Ответ: 0,6.

Решение 4: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

Число всех способов расставить ладьи равно n=64⋅63=4032n=64⋅63=4032 (первую ладью ставим на любую из 64 клеток, а вторую - на любую из оставшихся 63 клеток).

Число способов расставить ладьи так, что они не будут бить одна другую равно m=64⋅(64−15)=64⋅49=3136m=64⋅(64−15)=64⋅49=3136 (первую ладью ставим на любую из 64 клеток, вычеркиваем клетки, которые находятся в том же столбце и строке, что и данная ладья, затем вторую ладью ставим на любую из оставшихся после вычеркивания 49 клеток).

Тогда искомая вероятность P=3136/4032=49/63=7/9=0,778.P=3136/4032=49/63=7/9=0,778.

Ответ: 7/9.

Решение 5: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

Подсчитаем n=C66+5−1=C610=210n=C6+5−16=C106=210 - число различных способов разложить 6 рукописей по 5 папкам, причем в каждой папке может быть любое количество рукописей.

Теперь подсчитаем m=5⋅C4−16−1=5⋅C35=50m=5⋅C6−14−1=5⋅C53=50 - число способов разложить 6 рукописей по 4 папкам, причем в каждой папке должно быть не менее одной рукописи. При этом нужно полученное число сочетаний умножить на 5, так как папку, которая останется пустой, можно выбрать 5 способами.

Искомая вероятность Р=50/210=5/21.Р=50/210=5/21.

Ответ: 5/21.

Ответы

  Вариант № 2

Решение 1: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

Случай а) n=9n=9, так как всего 9 различных карточек. m=4m=4, так как всего на 4 карточках написаны четные числа (2, 4, 6, 8). Тогда P=4/9.P=4/9.

Случай б) n=9n=9, так как всего 9 различных карточек. m=0m=0, так как на всех карточках написаны однозначные числа. Тогда P=0/9=0P=0/9=0.

Ответ: 4/9, 0.

Решение 2: Используем классическое определение вероятности: P=m/nP=m/n, где nn - число всех равновозможных элементарных исходов, mm - число элементарных исходов, благоприятствующих осуществлению события AA = (Тома стоят в порядке возвозрастания номера слева направо, но не обязательно рядом).

n=40⋅39⋅38=59280n=40⋅39⋅38=59280, так как первый том можно поставить на любое из 40 мест, второй - на любое из 39 мест и третий - на любое из оставшихся 38 мест. А число

m=C340=40!37!3!=40⋅39⋅381⋅2⋅3=9880.m=C403=40!37!3!=40⋅39⋅381⋅2⋅3=9880.

Тогда искомая вероятность

P(A)=mn=988059280=16.P(A)=mn=988059280=16.

Ответ: 1/6.

Решение 3: Используем классическое определение вероятности: P=m/nP=m/n, где mm - число исходов, благоприятствующих осуществлению события, а nn - число всех равновозможных элементарных исходов.

n=5⋅4⋅3⋅2=120n=5⋅4⋅3⋅2=120 способов, так как первую карточку (букву) можно вытянуть (выбрать) 5 способами (так как всего карточек пять), вторую - 4 (осталось к этому шагу четыре), третью - 3 и четвертую - 2 способами.
m=1m=1, так как искомая последовательность карточек "ю", потом "р", потом "т", потом "а" только одна.

Получаем вероятность P=1/120P=1/120.

Ответ: 1/120.

Решение 4: Используем формулу классической вероятности: P=m/nP=m/n, где nn - число всех равновозможных элементарных исходов, mm - число элементарных исходов, благоприятствующих осуществлению события.

Число различных перестановок из букв А, К, К, Л, У равно

n=5!1!2!1!1!=1⋅2⋅3⋅4⋅51⋅2=60,n=5!1!2!1!1!=1⋅2⋅3⋅4⋅51⋅2=60,

из них только одна соответствует слову "кукла" (m=1m=1), поэтому по классическому определению вероятности вероятность того, что ребенок соберет из кубиков слово "кукла" равна P=1/60P=1/60.

Ответ: 1/60.

 Решение 5. Используем классическое определение вероятности: m P n = , где m – число исходов, благоприятствующих осуществлению события, а n – число всех возможных элементарных исходов. n = = ⋅ ⋅ ⋅ ⋅ = 5! 1 2 3 4 5 120 - число различных перестановок из 5 книг на полке. Найдем число благоприятствующих описанному в задаче событию исходов – есть только одна расстановка, когда книги стоят слева направо в порядке нумерации томов (от 1 до 5), то есть m =1. Искомая вероятность 1 0,0083. 120 P = ≈ ОТВЕТ: 0,0083  

Контрольная работа № 14

Итоговое повторение

Вариант № 1

пределы.

Решение:  Упражнение 1. Найти указанные

При подстановке вместо переменно х ее предельного значения 3 получается неопределенность вида . Для избавления от этого типа неопределенности в этом случае представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой , где - корни квадратного трехчлена . У нас , т.к. дискриминант квадратного трехчлена , а следовательно,  .

Аналогично .

Теперь условие примера можно переписать а другом виде и продолжить решение:

.

.

Здесь сталкиваемся с неопределенностью вида , избавиться от которой можно вынесением за скобки в числителе и знаменателе дроби старшей степени переменной: .

 .

В данном случае для освобождения от возникшей неопределенности вида будем использовать I замечательный предел и одно из его очевидных следствий:

.

Решение примера будет выглядеть следующим образом:

 

Упражнение 2. Найти производные, пользуясь правилами и формулами дифференцирования.

Решение:

Кроме формул дифференцирования нужно использовать правила дифференцирования (суммы, разности, произведения, частного).

Необходима и теорема о производной сложной функции:

если задана сложная функция , где , то есть ; если каждая из функций  и  дифференцируема по своему аргументу, то

.

 

1.     , ,

.

,

 

Упражнение 3. Исследовать функцию методами дифференциального исчисления и начертить график.

Исследование функции и построение графика рекомендуется проводить по следующей схеме:

1.     найти область определения функции D(y);

2.     найти точки экстремума функции и определить интервалы ее монотонности;

3.     найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции;

4.     найти асимптоты графика функции;

5.     построить график, используя результаты предыдущих исследований;

6.     дополнительно найти наибольшее и наименьшее значения на отрезке .

Решение:

Дана функция: 

1.     Областью определения данной функции являются все действительные значения аргумента х, то есть D(y): , а это значит, что функция непрерывна на всей числовой прямой и график ее не имеет вертикальных асимптот.

2.     Исследуем функцию на экстремум и интервалы монотонности. С этой целью найдем ее производную и приравняем к нулю:

Решая полученное квадратное уравнение, делаем вывод о том, что функция имеет две критические точки I рода х₁ = -5, х₂ = -1. Разбиваем область определения этими точками на части и по изменению знака производной в них выявляем промежутки монотонности и наличие экстремума:

Упражнение 4. Задан закон s(t) изменения пути движения материальной точки; нужно найти значения скорости и ускорения этой точки в момент времени t₀.

 

Решение:

Пусть .

Известно, что значения скорости и ускорения материальной точки в некоторый момент времени являются соответственно значениями в этот момент I и II производных функции, задающей закон изменения пути движения точки.

У нас 

(ед. ск.)

(ед. уск.)

 

 

Упражнение 5. Найти неопределенные интегралы

а) способом подстановки (методом замена переменной) , ;

б) применяя метод интегрирования по частям , .

Решение:

а) : применим подстановку . Тогда  и 

: применим подстановку . Тогда ,

, откуда 

б) : применим формулу интегрирования по частям .

Положим . Тогда .

Следовательно, .

: положим . Тогда .

Отсюда . Применяя в последнем интеграле подстановку , получаем , следовательно, .

Отсюда .

 

Вариант № 2

 

Упражнение 1. Найти общее решение (общий интеграл) дифференциального уравнения I порядка .

Решение:

Правая часть уравнения  обладает свойством . Поэтому заданное уравнение является однородным дифференциальным уравнением I порядка. Совершим замену , где - некоторая функция от аргумента х. Отсюда . Исходное уравнение приобретает вид .

Продолжаем преобразования: ; .

Производим разделение переменных: .

После интегрирования обеих частей уравнения получаем

;

.

Таким образом ; .

Потенцируя, находим  или ; .

Итак, общий интеграл исходного уравнения приобретает вид

, где С – произвольная постоянная.

 

Упражнение 2. Найти частное решение линейного однородного дифференциального уравнения II порядка с постоянными коэффициентами:

а) 

б) 

в) 

Решение:

а) Для заданного дифференциального уравнения составим соответствующее характеристическое уравнение по принципу: . Решаем полученное квадратное уравнение и получаем два вещественных разных корня .

Т.к. , то общее решение данных уравнений записывается в виде . В нашем случае , где - произвольные постоянные.

Отсюда , .

Используя начальные условия : , т.е. .

Из того что  следует , т.е. , .

Решая систему уравнений , получаем .

Теперь в наше общее решение  подставим найденные значения . Частное решение исходного уравнения, удовлетворяющее заданным начальным условиям, приобретает вид .

б) Для заданного дифференциального уравнения составим соответствующее характеристическое уравнение по принципу: . Решаем полученное квадратное уравнение и получаем два равных вещественных корня .

Т.к. , то общее решение данных уравнений записывается в виде . В нашем случае , где - произвольные постоянные.

Отсюда , .

Учитывая начальные условия, получаем систему уравнений для определения : . Решая систему, получаем .

Искомое частное решение имеет вид: 

в) Для заданного дифференциального уравнения  составим соответствующее характеристическое уравнение . Решая это уравнение, убеждаем, что оно не имеет вещественных корней.

В этом случае общее решение соответствующего дифференциального уравнения записывается в виде , где  - коэффициенты характеристического уравнения).

У нас  поэтому общее решение заданного дифференциального уравнения имеет вид .

Отсюда .

Таким образом, для определения значений  исходя из начальных условий, получаем систему уравнений ,

решая которую имеем .

Итак, искомое частное решение приобретает вид

 

 Упражнение 3. Определенный интеграл

 Вычислить определенный интеграл

⁴ x dx

 

Упражнение 4. Применение интеграла к вычислению площадей

Найдите площадь фигуры, ограниченной линиями  x=0,   x=/2,  f₁(x) = sin x, f₂(x) = cos x

 

Упражнение 5. Основные теоремы теории вероятностей

Найдите член  разложения  (x+ ₄)¹⁰,   не содержащий х (т.е. содержащий х в нулевой степени)

 

 

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.2.3

ЗАДАНИЯ ДЛЯ ИТОГОВОГО КОНТРОЛЯ (ЭКЗАМЕН).

1 вариант экзаменационной работы

для проведения письменного экзамена по математике

 

Обязательная часть

При выполнении заданий 1-8 запишите ход решения и полученный ответ

 

1. (1 балл) Учебник  стоит 6о рублей. Определите, сколько таких учебников можно купить за 200 рублей, если его цена снизилась на 10 %.

2. (1 балл) Определите, сколько банок краски по 3 кг необходимо купить для покраски пола в кабинете математики площадью 5х7 , если на 1  расходуется 300 грамм краски.

3. (1 балл) Определите, какие из перечисленных точек принадлежат графику функции у (х) = 5х-2

А(2;8);  В(0;1); С(3;7), Д(0;-2).

^{4. (1 балл) Вычислите значение выражения}

5. (1 балл) Найдите значение cos a , если известно, что sin a=  и 0 < a <

6. (1 балл) Решите уравнение

7. (1 балл) Вычислите значение выражения

8. (1 балл) Решите уравнение

9. (1 балл) Определите, какой из ниже приведенных графиков соответствует четной функции. Отметьте его знаком «+» и кратко поясните, почему.

Используя график функции у = f(x) (см. рис.), определите и запишите ответ:

10. (1 балл) наименьшее и наибольшее значения функций;

11. (1 балл) промежутки возрастания и убывания функций;

12. (1 балл) при каких значениях  x   f(x) 0.

 

При выполнении заданий 13-18 запишите ход решения и полученный ответ

13. (1 балл) От электрического столба высотой 8 метров к зданию, высота которого 4 метра натянут кабель. Определите длину кабеля, если расстояние между зданием и столбом 3 метра.

14. (1 балл) Тело движется по закону S(t)= 2-7х+3. Определите, в какой момент времени скорость будет равна 21.

15. (1 балл) Найдите область определения функции у = Lg (-2x).

16. (1 балл) Решите уравнение 

17. (1 балл) Решите уравнение

18. (1 балл) Прямоугольный треугольник с катетами  с катетами 2 см и 4 см в первый раз вращается вокруг большого катета, а во второй – вокруг меньшего. Определите полученные геометрические тела и сравните площади их боковых поверхностей.

Дополнительная часть

При выполнений заданий 19-22 запишите ход решения и полученный ответ

19. Найдите промежутки убывания функции у =

20. (3 балла)  Основанием прямой призмы является ромб со стороной 14 см и углом 30 . Меньшее из диагональных  сечений  призмы является квадратом. Найдите объем призмы.

21. (3 балла) Решите систему уравнений

22. (3 балла) Найдите решение уравнения: 1+cosx +cos2x = 0

 

 

2 вариант экзаменационной работы

для проведения письменного экзамена по математике

 

Обязательная часть

При выполнении заданий 1-8 запишите ход решения и полученный

 

1. (1балл) Блокнот стоит 40 рублей. Какое наибольшее количество таких блокнотов  можно будет купить на 500 рублей после повышения цены на 15%?

2. (1 балл) Определите, сколько банок краски по 3 кг необходимо купить для покраски пола в актовом зале площадью 10х7 , если на 1  расходуется 300 грамм краски.

3. (1 балл) Определите, какие из перечисленных точек принадлежат графику функции у (х)=4х-2.

А(10;2);  В(2;6); С(3;4), Д(0;-2).

^{4. (1 балл) Вычислите значение выражения}

5. (1 балл) Найдите значение cos a , если известно, что sin a=  и 0 < a <

6.(1 балл) Решите уравнение

7 .(1 балл) Вычислите значение выражение

8. (1 балл) Решите уравнение

9. (1 балл) Определите, какой из ниже приведенных графиков соответствует четной функции. Отметьте его знаком «+» и кратко поясните, почему.

 

Используя график функции у = f(x) (см. рис.), определите и запишите ответ:

10. (1 балл) наименьшее и наибольшее значения функций;

11. (1 балл) промежутки возрастания и убывания функций;

12. (1 балл) при каких значениях  x   f(x) 0.

 

При выполнении заданий 13-18 запишите ход решения и полученный ответ

13. (1 балл) От электрического столба высотой 8 метров к зданию, высота которого 2 метра натянут кабель. Определите длину кабеля, если расстояние между зданием и столбом 8 метров.

14. (1 балл) Тело движется по закону S(t)= 2+x+4. Определите, в какой момент времени скорость будет равна 59.

15. (1 балл) Найдите область определения функции у = Lg (-2x).

16. (1 балл) Решите уравнение 

17. (1 балл) Решите уравнение

18. (1 балл) Прямоугольный треугольник с катетами  с катетами 3 см и 5 см в первый раз вращается вокруг большого катета, а во второй – вокруг меньшего. Определите полученные геометрические тела и сравните площади их боковых поверхностей

Дополнительная часть

При выполнений заданий 19-22 запишите ход решения и полученный ответ

19. Найдите промежутки убывания функции у =

20. (3 балла)  Основанием прямой призмы является ромб со стороной 16 см и углом 60 . Меньшее из диагоналей сечения призмы является квадратом. Найдите объем призмы.

21. (3 балла) Решите систему уравнений

22. (3 балла) Найдите решение уравнения: 1- cos2х = 2sinx.                           

 

 

3 вариант экзаменационной работы

для проведения письменного экзамена по математике

 

Обязательная часть

При выполнении заданий 1-8 запишите ход решения и полученный

 

1. (1 балл) Пачка сливочного масла стоит 25 рублей. Пенсионерам магазин делает скидку 5%.Сколько пачек масла сможет купить пенсионер за 1оо рублей?

2. (1 балл) Определите, сколько банок краски по 2 кг необходимо купить для покраски пола в спортивном зале площадью 20х7 , если на 1  расходуется 300 грамм краски .

3. (1 балл) Определите, какие из перечисленных точек принадлежат графику функции у (х)=2х+2.

А(0;2);  В(0;1); С(-2;-2), Д(0;2)

^{4. (1 балл) Вычислите значение выражения}

5. (1 балл) Найдите значение sin a , если известно, что cos a= 0,6 и 0 < a <

6. (1 балл) Решите уравнение

7 .(1 балл) Вычислите значение выражения

8. (1 балл) Решите уравнение

9. (1 балл) Определите, какой из ниже приведенных графиков соответствует нечетной функции. Отметьте его знаком «+» и кратко поясните, почему.

Используя график функции у = f(x) (см. рис. ниже), определите и запишите ответ:

10. (1 балл) наименьшее и наибольшее значения функций;

11. (1 балл) промежутки возрастания и убывания функций;

12. (1 балл) при каких значениях  x   f(x) 0.

При выполнении заданий 13-18 запишите ход решения и полученный ответ

13. (1 балл) От электрического столба высотой 10 метров к зданию, высота которого 6 метра натянут кабель. Определите длину кабеля, если расстояние между зданием и столбом 3 метра.

14. (1 балл) Тело движется по закону S(t)= 5. Определите, в какой момент времени скорость будет равна 17.

15. (1 балл) Найдите область определения функции у= Lg (3)

16. (1 балл) Решите уравнение 

17. (1 балл) Решите уравнение -

18. (1 балл) Прямоугольный треугольник с катетами  с катетами 4 см и 5 см в первый раз вращается вокруг большого катета, а во второй – вокруг меньшего. Определите полученные геометрические тела и сравните площади их боковых поверхностей.

Дополнительная часть

При выполнений заданий 19-22 запишите ход решения и полученный ответ

19. Найдите промежутки убывания функции у =

20. (3 балла)  Основанием прямой призмы является ромб со стороной 11 см и углом 60 . Меньшее из диагоналей сечения призмы является квадратом. Найдите объем призмы.

21. (3 балла) Решите систему уравнений

22. (3 балла) Найдите решение уравнения:

 

4 вариант экзаменационной работы

для проведения письменного экзамена по математике

 

Обязательная часть

При выполнении заданий 1-8 запишите ход решения и полученный ответ

 

1. Тетрадь стоит 20 рублей. Какое наибольшее число таких тетрадей можно будет купить на 650 рублей после понижения цены на 20%?

2. Определите, сколько банок краски по 3 кг необходимо купить для покраски пола в кабинете математики площадью 5х7, если на 1  расходуется 300 грамм краски.

3. (1 балл) Определите, какие из перечисленных точек принадлежат графику функции у (х)=3х-2.

А(0;-2);  В(0;1); С(3;4), Д(1;1).

^{4.(1 балл) Вычислите значение выражения}

5. (1 балл) Найдите значение cos a , если известно, что sin a =   и   < a <

6. (1 балл) Решите уравнение

7 .(1 балл) Вычислите значение выражения

8. (1 балл) Решите уравнение

9. (1 балл) Определите, какой из ниже приведенных графиков соответствует нечетной функции. Отметьте его знаком «+» и кратко поясните, почему.

Используя график функции у = f(x) (см. рис.), определите и запишите ответ:

10. (1 балл) наименьшее и наибольшее значения функций;

11. (1 балл) промежутки возрастания и убывания функций;

12. (1 балл) при каких значениях  x   f(x) 0.

 

При выполнении заданий 13-18 запишите ход решения и полученный ответ

13. (1 балл) От электрического столба высотой 11 метров к зданию, высота которого 7 метров натянут кабель. Определите длину кабеля, если расстояние между зданием и столбом 3 метра.

14. (1 балл) Тело движется по закону S(t)= 4. Определите, в какой момент времени скорость будет равна 19.

15. (1 балл) Найдите область определения функции у= Lg (5).

16. (1 балл) Решите уравнение  .

17. (1 балл) Решите уравнение

18. (1 балл) Прямоугольный треугольник с катетами  с катетами 1 см и 5 см в первый раз вращается вокруг большого катета, а во второй – вокруг меньшего. Определите полученные геометрические тела и сравните площади их боковых поверхностей.

Дополнительная часть

При выполнений заданий 19-22 запишите ход решения и полученный ответ

19. Найдите промежутки убывания функции у =.

20. (3 балла)  Основанием прямой призмы является ромб со стороной 15 см и углом 60 . Меньшее из диагоналей сечения призмы является квадратом. Найдите объем призмы.

21. (3 балла) Решите систему уравнений

22. (3 балла) Найдите решение уравнения:

Критерии оценки итоговой работы:

 

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9–14
«4» (хорошо)	15–20 (не менее одного задания из дополнительной части)
«5» (отлично)	21–30 (не менее двух заданий из дополнительной части)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 РАЗДЕЛ 4.  Критерии оценивания.

 

 

Промежуточная аттестация проводится в конце 2 семестра в форме экзамена.  Оценка результатов освоения программы происходит с использованием пятибалльной системы оценивания знаний. Используются следующие критерии оценки:

Оценка	Критерий
«5»	Работа выполнена в заданное время, самостоятельно, с соблюдением определенных требований, качественно и творчески
«4»	Работа выполнена в заданное время, самостоятельно, с соблюдением определенных требований, при выполнении отдельных алгоритмов действий допущены небольшие отклонения, общий вид объекта достаточно аккуратный
«3»	Работа выполнена в заданное время, самостоятельно, с нарушением заданной последовательности, отдельные алгоритмы действия выполнены с отклонением от образца, объект оформлен небрежно или не в заданный срок
«2»	Обучаемый самостоятельно не справился с работой, последовательность нарушена, при выполнении алгоритмов действия допущены большие отклонения, объект оформлен небрежно и имеет незавершенный вид

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике

1. Оценка письменных контрольных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

·                     работа выполнена полностью;

·                     в логических рассуждениях и обосновании решения нет пробелов и ошибок;

·                     в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

·                     работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

·                     допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

·                      допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

 Отметка «2» ставится, если:

·                     допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Отметка «1» ставится, если:

·                     работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.

Преподаватель  может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Ответ оценивается отметкой «5», если ученик:

·                     полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

·                     изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

·                     правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

·                     показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

·                     продемонстрировал знание теории ранее изученных сопутствующих тем,  сформированность и устойчивость используемых при ответе умений и навыков;

·                     отвечал самостоятельно, без наводящих вопросов преподавателя;

·                     возможны одна – две  неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания преподавателя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

·                     в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

·                     допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания преподавателя;

·                     допущены ошибка или более двух недочетов  при освещении второстепенных вопросов или в выкладках,  легко исправленные после замечания преподавателя.

Отметка «3» ставится в следующих случаях:

·                     неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

·                     имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов преподавателя;

·                     студент не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

·                     при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

 Отметка «2» ставится в следующих случаях:

·                     не раскрыто основное содержание учебного материала;

·                     обнаружено незнание учеником большей или наиболее важной части учебного материала;

·                     допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

 

3. Общая классификация ошибок.

При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.

3.1. Грубыми считаются ошибки:

-незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов  

обозначений величин, единиц их измерения;

-незнание наименований единиц измерения;

-неумение выделить в ответе главное;

-неумение применять знания, алгоритмы для решения задач;

-неумение делать выводы и обобщения;

-неумение читать и строить графики;

-неумение пользоваться первоисточниками, учебником и справочниками;

-потеря корня или сохранение постороннего корня;

-отбрасывание без объяснений одного из них;

-равнозначные им ошибки;

-вычислительные ошибки, если они не являются опиской;

- логические ошибки.

  К негрубым ошибкам следует отнести:

-неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

-неточность графика;

-нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

-нерациональные методы работы со справочной и другой литературой;

-неумение решать задачи, выполнять задания в общем виде.

  Недочетами являются:

-нерациональные приемы вычислений и преобразований;

-небрежное выполнение записей, чертежей, схем, графиков.

 

 

 

5. УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

а) основная литература:

1.     Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и др. Алгебра и начала анализа. Учебник для 10 – 11 классов общеобразовательных учреждений: базовый уровень – М.: Просвещение, 2016

2.     Анатасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия,10-11: учебник для общеобразоват. учреждений /-М.: Просвещение , 2017 (баз.и проф. ур.)

б) дополнительная литература для студентов:

·        учебники:

1.     Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков.-2-е изд. Испр. – М.: Издательский центр «Академия», 2017

2.     Башмаков М.И. Математика: учебник для 11 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков.-2-е изд. Испр. – М.: Издательский центр «Академия», 2016

3.     Колмогоров А.Н. Алгебра и начала анализа. Учебник для 10 – 11 классов общеобразовательных учреждений – М.: Просвещение, 2018

4.     Погорелов А.В. Геометрия. Учебник для 10 – 11 классов общеобразовательных учреждений – М: Просвещение  2018 г.

·        учебные пособия:

1.     Брадис В.М. Четырехзначные математические таблицы для средней школы – М: Дрофа 2018

2.     Дорофеев, Г.В. Сборник заданий для подготовки и проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 класс/ Г.В. Дорофеев, Г.К. Муравин, Е.А. Седова.- М.: Дрофа, 2018

3.     Математика: тренировочные тематические задания повышенной сложности с ответами для подготовки к ЕГЭ и к другим формам выпускного  и вступительного экзаменов/ сост. Г.К. Ковалева, Т.И. Бузулина, О.Л. Безрукова, Ю.А. Розка.-Волгоград: Учитель, 2017

·        справочно-библиографическая литература:

1.     Выгодский М.Я. Справочник по элементарной математике. М. Просвещение, 2018г.

2.      Выгодский М.Я. Справочник по высшей математике. М. Роскнига, 2018г.

3.     Энциклопедия для детей. В 15 т. Т.11.Математика / под. редакцией М.Д. Аксенова.- И.: Мир энциклопедий Аванта +, 2017

в) дополнительная литература для преподавателя:

·        учебники:

1.     Башмаков М.И. Математика: учебник для 10 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков.-2-е изд. Испр. – М.: Издательский центр «Академия», 2018

2.     Башмаков М.И. Математика: учебник для 11 класса: среднее (полное) общее образование (базовый уровень) / М.И. Башмаков.-2-е изд. Испр. – М.: Издательский центр «Академия», 2018

3.     Колмогоров А.Н. Алгебра и начала анализа. Учебник для 10 – 11 классов общеобразовательных учреждений – М.: Просвещение, 2016

4.     Погорелов А.В. Геометрия. Учебник для 10 – 11 классов общеобразовательных учреждений – М: Просвещение  2017 г.

·        учебные пособия:

1.     Брадис В.М. Четырехзначные математические таблицы для средней школы – М: Дрофа 2018

2.     Геометрия. 10-11 классы: тесты для текущего и обобщающего контроля/авт.-сост.Г.И. Ковалева, Н.И. Мазурова.-Волгоград: Учитель, 2017

3.     Глазков Ю.А., Боженкова Л.И.Тесты по геометрии: 10 класс: к учебнику Л.С. Атанасяна и др. «Геометрия .10-11 классы».-М.: Издательство «Экзамен», 2016

4.     Ивлев Б.М.,Саакян С.М., Шварцбург С.И. Дидактические материалы по Алгебре и началам анализа для 10 класса – М: Просвещение, 2018 

5.     Рабочие программы по геометрии: 6-11 классы/ Сост. Н.Ф. Гаврилова.- М: ВАКО, 2019

6.     Поурочные разработки по геометрии. 10 класс/ Сост.В.А. Яровенко.- .- М: ВАКО, 2018

 

 

 

 

 

Скачано с www.znanio.ru