
Самарский колледж строительства и предпринимательства (филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Национальный исследовательский
Московский государственный строительный университет»
КОМПЛЕКТ ОЦЕНОЧНЫХ СРЕДСТВ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
«МАТЕМАТИКА»
уровень подготовки базовый
форма обученияочная
Разработчик (и): преподаватель первой квалификационной категории Буркина Д.Д.
Самара, 2019
ОЦЕНОЧНЫЕ СРЕДСТВА для текущего контроля
1. ВХОДНОЙ КОНТРОЛЬ
Тестовые задания для входного контроля по дисциплине «Математика»
для студентов 1 курса. 1 вариант
1.
Решите
уравнение ![]()
А) 9 Б) -8 В) -9 Г) 3
2.
Решите
уравнение ![]()
А) -1 и 2,5 Б) 2 и -5 В) -2 и 5 Г) 1 и -2,5
3.
Решите
неравенство ![]()
А) (-∞; 11) Б) (17; +∞) В) (11; +∞) Г) (-∞; -11)
4.
Решите
неравенство ![]()
А)
(-∞; ![]() )
)![]() (3; +∞) Б) (-3;
(3; +∞) Б) (-3; ![]() В) (-
В) (-![]() Г) (-1; 9)
Г) (-1; 9)
5.
Упростите
выражение ![]()
А) -11у2-20 Б) 13у2-20 В) -11у2-16у+20 Г) 8у2-20
6.
Упростите
выражение и найдите его значение при b=3.
![]()
А) 2 Б) -0,4 В) -3 Г) 5
7.
Упростите
выражение и найдите его значение при m=3,
n=2 ![]()
А) 3 Б) -2 В) 0,4 Г) 2
8. Представьте выражение в виде степени и найдите его значение
при а=![]()
А) -27 Б) -9 В) 1/9 Г) 9
9.
Вычислите
значение выражения ![]()
А) 180 Б) 1450 В) 2520 Г) 4540
10.
Проходит ли
график функции ![]() через точку А(-35; 76)?
через точку А(-35; 76)?
А) да Б) нет
11.
Укажите
координаты точки пересечения графиков функций ![]()
А) (0;4) Б) (2;-1) В) (-1;2) Г) (1;-2)
12.
График функции, убывающей на промежутке ![]() ,
изображен на рисунке…
,
изображен на рисунке…
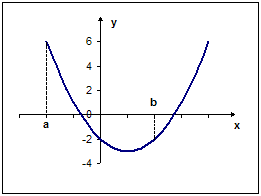
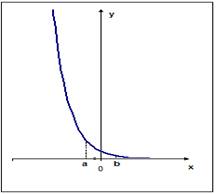
Рис. 1 Рис. 2
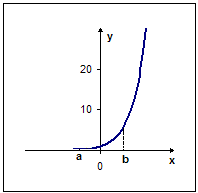
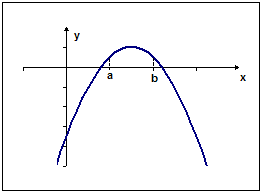
Рис. 3 Рис. 4
А) рис. 1 Б) рис. 2 В) рис. 3 Г) рис. 4
13. Дана равнобедренная трапеция, основания которой равны 5 см и 17 см, боковая сторона равна 10 см. Найти площадь трапеции.
А) 48 кв.см Б) 88 кв.см В) 56 кв.см Г) 110 кв.см
14. Дан треугольник, основание которого равно 10 см, а высота, проведённая к нему равна 15 см. Найти сторону равновеликого квадрата.
А)
25 см Б) ![]() см В) 9
см Г)
см В) 9
см Г) ![]() см
см
15. Обхват дерева у основания приближённо равен 3,5 м. Найти площадь сруба. Ответ округлить до сотых.
А) 0,88 кв.м Б) 1,82 кв.м В) 0,98 кв.м Г) 0,48 кв.м
Тестовые задания для входного контроля по дисциплине «Математика»
для студентов 1 курса. 2 вариант
1.
Решите
уравнение ![]()
А) 2 Б) -8 В) 8 Г) -1
2.
Решите
уравнение 5![]()
А) -1 и -0,4 Б) 5 и 2 В) 1 и 0,4 Г) -5 и 2
3.
Решите
неравенство ![]()
А) (13;+∞) Б) (10;+∞) В) (-∞;10) Г) (-∞;-10)
4.
Решите
неравенство ![]()
А) (-1,5; -1) Б) (1; 1,5) В) (-3; -2) Г) (-1; -1,5)
5.
Упростите
выражение ![]()
А) 11а2-10а+36 Б) -9а2-36 В) а2+15а-36 Г) 11а2-36
6.
Упростите
выражение и найдите его значение при а=4. ![]()
А) -2 Б) 1 В) -3 Г) 3
7.
Упростите
выражение и найдите его значение при а=4, b=1 ![]()
А) 1 Б) 0,25 В) -1 Г) 0,5
8.
Представьте
выражение в виде степени и найдите его значение при х=![]()
А) 8 Б) 1/6 В) -8 Г) 9
9.
Вычислите
значение выражения ![]()
А) 1500 Б) 800 В) 900 Г) 190
10.
Проходит ли
график функции ![]() через точку В(-45; -86)?
через точку В(-45; -86)?
А) да Б) нет
11.
Укажите
координаты точки пересечения графиков функций ![]()
А) (1; 3) Б) (-4; 2) В) (-2; -4) Г) (2; 4)
 12. График линейной функции
изображен на рисунке…
12. График линейной функции
изображен на рисунке…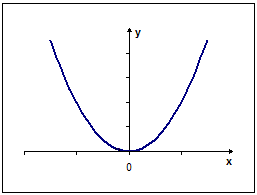
Рис. 1 Рис. 2
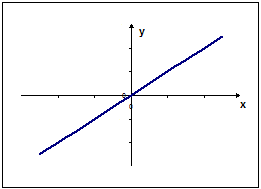
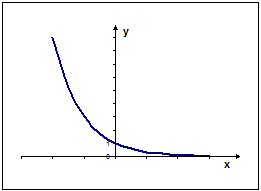
Рис. 3 Рис.4
А) рис. 1 Б) рис. 2 В) рис. 3 Г) рис. 4
13. Дана равнобедренная трапеция, боковая сторона которой равна 13 см, высота равна 5 см и меньшее основание равно 6 см. Найти площадь трапеции.
А) 180 кв.см Б) 45 кв.см В) 90 кв.см Г) 60 кв.см.
14. Дан треугольник, основание которого равно 12 см, а высота, проведённая к нему, равна 8 см. Найти длину равновеликого ему прямоугольника, если его ширина равна 3 см.
А) 16 см Б) 12 см В) 18 см Г) 10 см.
15. Площадь поперечного сечения дерева равна приближённо 1,3 кв.м. Найти обхват дерева в сечении. Ответ округлить до сотых.
А) 3,96 м Б) 4,02 м В) 2,88 м Г) 3,74 м.
2. Практические занятия
Практическое занятие № 1.
Действия над комплексными числами. Вариант 1.
1. Даны два комплексных числа: z1 = -4+2i, z2 = 1-3i
Вычислить:
z1 + z2 , z1 - z2 , z1 · z2 , z1 / z2 , z12 + z22 , z1 · ![]() ,
3z2 – 2z1
,
3z2 – 2z1
2. Дано комплексное число z = 1-3i. Найти z2 и z3
3. Решить квадратные уравнения и изобразить в комплексной плоскости точки, соответствующие корням этих уравнений.
А) 2х2 – х – 3 = 0,
Б) х2 + 4х + 8 = 0,
В) 4х2 + 36 = 0.
4.
Для
комплексного числа ![]() указать противоположное
и сопряжённое и изобразить эти числа в комплексной плоскости.
указать противоположное
и сопряжённое и изобразить эти числа в комплексной плоскости.
5. Вычислить i267, i182.
6.
Вычислить
значение выражения ![]() .
.
7.
Вычислить
значение выражения ![]() .
.
8. Вместо знака __ вставить нужный математический символ.
N __Z Q __–Q-- = R √3 __ --Q— Q ∩ –Q--= __
R+ + R_ + __ = R --Q-- __ N 0,3 __ Z
Практическое занятие № 1.
Действия над комплексными числами. Вариант 2.
1. Даны два комплексных числа: z1 = 2-3i, z2 = -3+i
Вычислить: z1 + z2 , z1 - z2 , z1 · z2 , z1 / z2 ,
z12 + z22 ,![]() ·
z2 , 2z2 – 3z1
·
z2 , 2z2 – 3z1
2. Дано комплексное число z = 3-2i. Найти z2 и z3
3. Решить квадратные уравнения и изобразить в комплексной плоскости точки, соответствующие корням этих уравнений.
А) 3х2 + 2х – 1 = 0,
Б) х2 - 8х + 32 = 0,
В) 9х2 + 36 = 0.
4.
Для
комплексного числа ![]() указать противоположное
и сопряжённое и изобразить эти числа в комплексной плоскости.
указать противоположное
и сопряжённое и изобразить эти числа в комплексной плоскости.
5. Вычислить i345, i126.
6.
Вычислить
значение выражения ![]() .
.
7.
Вычислить
значение выражения ![]() .
.
8.Вместо знака __ вставить нужный математический символ.
N __Z Q __–Q-- = R √3 __ --Q— Q ∩ –Q--= __
R+ + R_ + __ = R --Q-- __ N 0,3 __ Z
Практическое занятие № 2.
Степень и логарифм числа. Вариант 1.
1. Вычислить значение выражения.
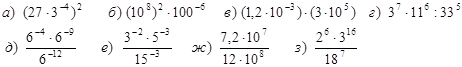
2. Упростить выражение и найти его значение при заданном значении переменной.
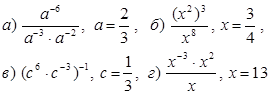
3. Вычислить:
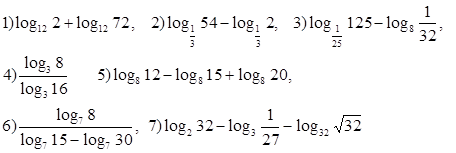
4. Вычислить:
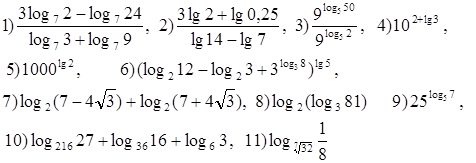
5. Найти х:
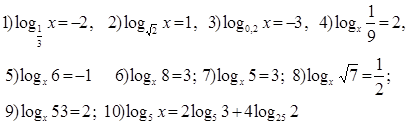
Практическое занятие № 2.
Степень и логарифм числа. Вариант 2.
1. Вычислить значение выражения.
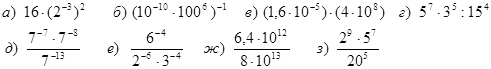
2. Упростить выражение и найти его значение при заданном значении переменной.

3. Вычислить:
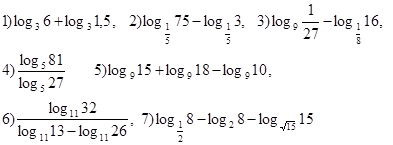
4. Вычислить:
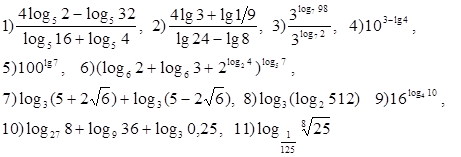
5. Найти х:
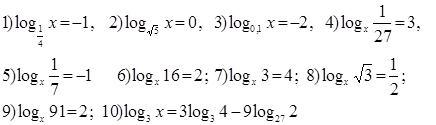
Практическое занятие № 3
Показательные уравнения и неравенства. Вариант 1.
|
2. Решить неравенства.
|
Практическое занятие № 3
Показательные уравнения и неравенства. Вариант 2.
|
2. Решить неравенства.
|
Практическое занятие № 4
Логарифмические уравнения и неравенства. Вариант 1.
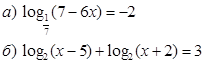
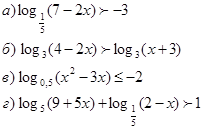
Практическое занятие № 4
Логарифмические уравнения и неравенства. Вариант 2.
1. Решить уравнения.
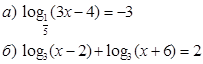
2. Решить неравенства.
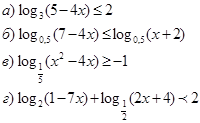
Практическое занятие № 5
Решение стереометрических задач. Вариант 1.
1.Точка А лежит в плоскости, а точка В находится на расстоянии 12.5 см от этой плоскости. Точка М – середина отрезка АВ. Найти расстояние от точки М до плоскости.
2. Перекладина лежит на двух вертикальных столбах, высота которых 3 м и 8 м. Расстояние между основаниями столбов равно 12 м. Какова длина перекладины?
3. Из точки А, не лежащей на данной плоскости, проведены на эту плоскость две наклонные, одна из которых на 7 см короче другой. Проекции наклонных равны 6 см и 15 см. Каковы длины наклонных?
4. Из вершины квадрата АВСД восстановлен перпендикуляр АЕ к плоскости квадрата. Чему равно расстояние от точки Е до прямой ВД, если АЕ = 2 см, АВ = 8 см?
5. АВСД –
квадрат. Из точки В восстановлен перпендикуляр ВМ к плоскости квадрата. Найти
ДМ и площадь треугольника ДМА, если АВ = ![]() , ВМ = 5 см.
, ВМ = 5 см.
6. КРМН –
квадрат. Из центра квадрата восстановлен перпендикуляр ОД к плоскости квадрата.
Найти периметр и площадь квадрата, если ОД = ![]() см, КД =
см, КД = ![]() см.
см.
7. Дан равносторонний треугольник АВС. Точка Р
равноудалена от всех вершин этого треугольника. Расстояние от точки Р до
плоскости треугольника равно ![]() см, АВ = 10 см. Найти расстояние
от точки Р до вершин треугольника, площадь треугольника АВС, площадь
треугольника АВР.
см, АВ = 10 см. Найти расстояние
от точки Р до вершин треугольника, площадь треугольника АВС, площадь
треугольника АВР.
Практическое занятие № 5
Решение стереометрических задач. Вариант 2.
1. Концы отрезка АВ, не пересекающего плоскость, удалены от неё на расстояния 2,4 см и 7,6 см. Найти расстояние от середины отрезка АВ до этой плоскости.
2. Перекладина длиной 25 см лежит на двух вертикальных столбах, высоты которых равны 8 см и 15 см. Каково расстояние между основаниями столбов?
3. Из точки К, не лежащей на данной плоскости, проведены на эту плоскость две наклонные, одна из которых на 2 см длиннее другой. Проекции этих наклонных равны 10 см и 6 см. Найти длины наклонных.
4. Из вершины равностороннего треугольника АВС восстановлен перпендикуляр АД к плоскости этого треугольника. Чему равно расстояние от точки Д до прямой ВС, если АД = 1 см, ВС = 8 см.
5. СДЕК –
квадрат со стороной 2 см. Из вершины Д восстановлен перпендикуляр ДВ к
плоскости квадрата. Найти ДВ и площадь треугольника ВДС, если ВК = ![]() см.
см.
6. АВСД –
квадрат, периметр которого ![]() см. Из центра квадрата
восстановлен перпендикуляр ОЕ к плоскости квадрата. Найти длину перпендикуляра,
если АЕ = 7 см.
см. Из центра квадрата
восстановлен перпендикуляр ОЕ к плоскости квадрата. Найти длину перпендикуляра,
если АЕ = 7 см.
7. Дан равносторонний треугольник АВС. Точка Р
равноудалена от всех вершин этого треугольника. Расстояние от точки Р до
плоскости треугольника равно ![]() см, АВ = 8 см. Найти расстояние от
точки Р до вершин треугольника, площадь треугольника АВС, площадь треугольника
ВСР.
см, АВ = 8 см. Найти расстояние от
точки Р до вершин треугольника, площадь треугольника АВС, площадь треугольника
ВСР.
Практическое занятие № 6
Решение комбинаторных задач. Вариант 1.
1. Сколькими способами можно расставить белые фигуры (2 коня,
2 слона, 2 ладьи, ферзя и короля) на первой линии шахматной доски?
2. Из спортивного клуба, насчитывающего 13 членов, надо coставить команду из 4 человек для участия в эстафете. Сколькими способами это можно сделать?
3. На конференции присутствуют 20 человек. Из них надо избрать делегацию из 5 человек. Сколькими способами это можно сделать?
4. В почтовом отделении продаются открытки 7 сортов.
А) Сколькими способами можно купить в нем 10 открыток?
Б) Сколькими способами можно купить 4 открытки?
В)Сколькими способами можно купить 5 различных открыток?
5. А) Сколько различных трехзначных чисел можно составить из карточек, на которых написаны цифры 5,6,7,0?
Б) Сколько чётных четырехзначных чисел можно составить из цифр 9,7,5,3,2?
В) Сколько пятизначных чисел можно составить из цифр 2, 9?
Г) Сколько чисел, кратных 5, можно составить из карточек 1,2,3,4,5?
6. *На собрании должны выступить 5 человек: А, Б, В, Г и Д. Сколькими способами можно расположить их в списке ораторов при условии, что Б не должен выступать до того, как выступит А?
7. *На собрании должны выступить 5 человек: А, Б, В, Г и Д. Сколькими способами можно расположить их в списке ораторов при условии, что А должен выступить непосредственно перед Б?
Практическое занятие № 6
Решение комбинаторных задач. Вариант 2.
1. Сколько ожерелий можно составить из 3 белых, 4 синих и 5 красных бусинок?
2. Из кружка по лёгкой атлетике, насчитывающего 16 спортсменов, надо coставить команду из 4 человек для участия в беге на 1000 м. Сколькими способами можно это сделать?
3. В организацию принято 25 человек. Из них надо избрать председателя, секретаря и культорга. Сколькими способами это можно сделать?
4. В магазине продаются фрукты 6 сортов.
А) Сколькими способами можно купить в нем 11фруктов?
Б) Сколькими способами можно купить 5 фруктов?
В) Сколькими способами можно купить 3 различных фрукта?
5. А) Сколько различных пятизначных чисел можно составить из цифр 1,2,3,0?
Б) Сколько нечётных четырехзначных чисел можно составить из карточек, на которых написаны цифры 3,4,5,9?
В) Сколько пятизначных чисел можно составить из цифр 9,0?
Г) Сколько существует четырехзначных чисел, кратных 5?
6. *На собрании должны выступить 5 человек: А, Б, В, Г и Д. Сколькими способами можно расположить их в списке ораторов при условии, что Б должен выступать раньше, чем выступит Г?
7. *На собрании должны выступить 5 человек: А, Б, В, Г и Д. Сколькими способами можно расположить их в списке ораторов при условии, что Д должен выступить обязательно после Г?
Практическое занятие № 7
Действия над векторами. Вариант 1.
1.
![]() Найти у.
Найти у.
2. Даны три последовательные вершины параллелограмма. Найти 4-ую вершину и длины диагоналей параллелограмма. А(-2;-3;-4), В(5;-4;-2), С(3;-1;-6).
3.
Найти угол
между векторами ![]()
4.
Дано ![]()
Найти: а)
![]() , б)
, б) ![]()
5.
Коллинеарны ли
векторы ![]()
6. При каком значении k векторы будут перпендикулярны? Найти длины этих векторов, взяв наибольшее из получившихся значений.
![]()
7. Дано: А(-2;-3; 1), В(1; 0; -3), С(3;-2; 0), D(0;-5; 4)
а) среди векторов указать равные и противоположные, если они есть
![]()
б) найти длины указанных векторов.
в) найти корд и длину вектора ![]()
г) найти значение выражения (![]() )2
)2
д) найти cosB.
8. Лежат ли точки А(2;-4;1), В(0;3;7), С(-2;-6;5) на одной прямой?
Практическое занятие № 7
Действия над векторами. Вариант 2.
1.
![]() Найти х.
Найти х.
2. Даны три последовательные вершины параллелограмма. Найти 4-ую вершину и длины диагоналей параллелограмма. А(1; -5; -2), В(-4; -5; -6), С(-2; 4; 0).
3.
Найти угол
между векторами ![]()
4.
Дано ![]()
Найти: а)
![]() , б)
, б) ![]()
5.
Коллинеарны ли
векторы?![]()
6. При каком значении k векторы будут перпендикулярны? Найти длины этих векторов, взяв наибольшее из получившихся значений.
![]()
7. Дано: А(0; -3; 7), В(2; -2; 2), С(4; 1; -1), D(2; 0; 4)
а) среди векторов указать равные и противоположные, если они есть
![]()
б) найти длины указанных векторов.
в) найти корд и длину вектора ![]()
г) найти значение выражения (![]() )2
)2
д) найти cosD.
8. Лежат ли точки А(1;-5;3), В(5;-1;-7), С(6;0;8) на одной прямой?
Практическое занятие № 8
Построение графиков путем преобразования. Вариант 1.
Построить графики следующих функций (путём преобразования графиков).
а) y = - 3 cosx, б) y
= sin (x - π/2) - 2, в) 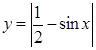
г) у = 0,5sinx, д) у = –3sin4x, е) у = sinx + 4, ж) у = –2sinx,
з)
у = cos(![]() + x), и) у = cos(x –
+ x), и) у = cos(x – ![]() ), к) у =│2cos(x –
), к) у =│2cos(x –![]() )│
)│
Практическое занятие № 8
Построение графиков путем преобразования. Вариант 2.
Построить графики следующих функций (путём преобразования графиков).
а) y = - 3 sinx, б) y
= cos (x + π/2) – 3, в) ![]()
г) у = 0,5cos x, д) у = –3cos4x, е) у = cosx + 4, ж) у = –2cosx,
з)
у = sin(![]() + x), и) у = sin(x –
+ x), и) у = sin(x – ![]() ), к) у =│2sin(x –
), к) у =│2sin(x –![]() )│
)│
Практическое занятие № 9
Преобразование тригонометрических выражений. Вариант 1.
1. Перевести углы из радиан в градусы и наоборот, определить четверть.
![]()
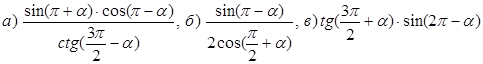
![]()
Найти
![]()
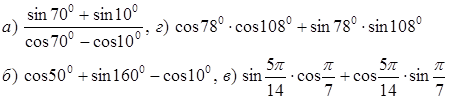
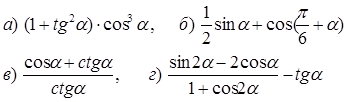
8. Построить график функции у = cosx и перечислить свойства функции.
Практическое занятие № 9
Преобразование тригонометрических выражений. Вариант 2.
1. Перевести углы из радиан в градусы и наоборот, определить четверть.
![]()
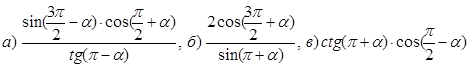
![]()
Найти
![]()
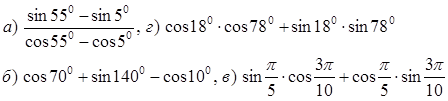
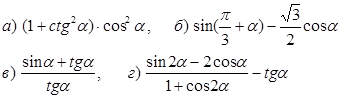
8. Построить график функции у = sinx и перечислить свойства функции.
Практическое занятие № 10
Тригонометрические уравнения и неравенства. 1 вариант
1.
Известно, что ![]() .
.
Найти
значение выражения: ![]()
2. Решить
уравнение ![]()
3. Решить тригонометрические уравнения и найти частные решения при данном значении k
А). ![]() Б).
Б). ![]()
В). ![]() Г).
Г). ![]()
4. Решить тригонометрическое уравнение
А). ![]() Б).
Б). ![]()
Практическое занятие № 10
Тригонометрические уравнения и неравенства. 2 вариант
1.
Известно, что ![]() .
.
Найти
значение выражения: ![]()
2. Решить
уравнение ![]()
3. Решить тригонометрические уравнения и найти частные решения при данном значении k
А). ![]() Б).
Б). ![]()
В). ![]() Г).
Г). ![]()
4. Решить тригонометрическое уравнение
А). ![]() Б).
Б). ![]()
Практическое занятие № 11
Функции, их свойства и графики. Вариант 1.
1.Сравнить:![]() ,
,![]()
![]()
2. Найти точки пересечения графика
функции с осями координат ![]()
3. Найти D(f). 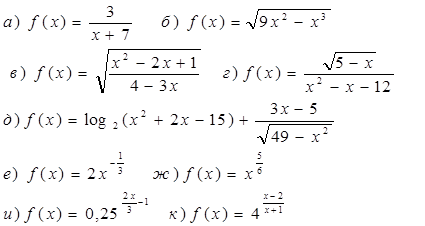
4. Привести примеры функций, у которых:
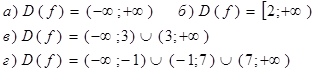
5. Построить эскиз графика функции, если известно, что
![]()
6. Дана функция ![]() .
.
а) Найти D(f)
б) исследовать на четность/нечетность
в) найти f(-1),
г) найти ![]()
д) найти те значения х, при которых у=4.
7. Построить график функции и
исследовать ее по общей схеме![]()
Практическое занятие № 11
Функции, их свойства и графики. Вариант 2.
1. Сравнить:![]()
![]()
![]()
2. Найти точки пересечения графика
функции с осямикоординат ![]()
3. Найти D(f). 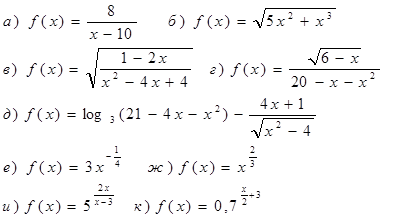
4. Привести примеры функций, у которых:
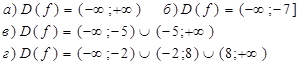
5. Построить эскиз графика функции, если известно, что
![]()
6. Дана функция ![]() .
.
а) Найти D(f)
б) исследовать на четность/нечетность
в) найти f(-1),
г) найти ![]()
д) найти те значения х, при которых у=-5.
7. Построить график функции и
исследовать ее по общей схеме![]()
Практическое занятие № 12
Многогранники. Вариант 1.
1. Дан прямой параллелепипед, основанием которой является ромб с диагоналями 10 см и 24 см. Боковое ребро равно 10 см. Найти площадь боковой поверхности, площадь полной поверхности и объём параллелепипеда.
2. Дан куб. Площадь полной его поверхности равна 150 см2. Найти объём куба и длину его диагонали.
3. Дана треугольная призма, у которой все рёбра равны. Площадь боковой поверхности призмы равна 48 см². Найти периметр ее основания
4. Дан прямоугольный параллелепипед, стороны основания которого равны 8 см и 9 см, диагональ параллелепипеда равна
17 см. Найти высоту и объём параллелепипеда.
5. Дан прямоугольный параллелепипед, измерения которого равны 5 см, 9 см, 10 см. Найти площадь полной поверхности, объём и длину его диагонали .
6. Дана прямая треугольная призма, в основании которой лежит равнобедренный треугольник со сторонами 10 см, 10 см, 16 см. Высота призмы равна 20 см. Найти площадь полной поверхности и объём этой призмы.
7. Дана правильная 6-угольная призма, диагональ основания которой равна 8 см, а боковое ребро равно 3√3 см. Найти площадь полной поверхности и объём призмы.
8. Дана правильная 4-угольная пирамида. высота пирамиды равна 12 см, диагональ основания равна 32 см. Найти боковое ребро и объём пирамиды.
9. Дана правильная 4-угольная пирамида, сторона основания равна 8√3 см, боковое ребро равно 11 см. Найти объём пирамиды.
10. Дана правильная треугольная пирамида, апофема которой равна 16 см, а площадь её боковой поверхности равна 168 см2. Найти сторону основания пирамиды.
11. Дана правильная 4-угольная пирамида, сторона основания равна 6 см, а апофема равна 3√5 см. Найти объём пирамиды и площадь её боковой поверхности.
Практическое занятие № 12
Многогранники. Вариант 2.
1. Дан прямой параллелепипед, основанием которой является ромб с диагоналями 30 см и 16 см. Боковое ребро равно 20 см. Найти площадь боковой поверхности, площадь полной поверхности и объём параллелепипеда.
2. Дан куб. Площадь полной его поверхности равна 96 см2. Найти объём куба и длину его диагонали.
3. Дана треугольная призма, у которой все рёбра равны. Площадь боковой поверхности призмы равна 75 см². Найти периметр ее основания.
4. Дан прямоугольный параллелепипед, стороны основания которого равны 5 см и 6 см, диагональ параллелепипеда равна 5√5 см. Найти высоту и объём параллелепипеда.
5. Дан прямоугольный параллелепипед, измерения которого равны
6 см, 8 см, 5 см. Найти площадь полной поверхности, объём и длину его диагонали .
6. Дана прямая треугольная призма, в основании которой лежит равнобедренный треугольник со сторонами 13 см, 13 см, 24 см. Высота призмы равна 10 см. Найти площадь полной поверхности и объём этой призмы.
7. Дана правильная 6-угольная призма, диагональ основания которой равна 8 см, а боковое ребро равно 3√3 см. Найти площадь полной поверхности и объём призмы.
8. Дана правильная 4-угольная пирамида. высота пирамиды равна 15 см, диагональ основания равна 16 см. Найти боковое ребро и объём пирамиды.
9. Дана правильная 4-угольная пирамида, сторона основания равна 4√3 см, боковое ребро равно 5 см. Найти объём пирамиды.
10. Дана правильная треугольная пирамида, апофема которой равна 12 см, а площадь её боковой поверхности равна 108 см2. Найти сторону основания пирамиды.
11. Дана правильная 4-угольная пирамида, сторона основания равна 8 см, а апофема равна 4√5 см. Найти объём пирамиды и площадь её боковой поверхности.
Практическое занятие № 13
Круглые тела. 1 вариант
1. Прямоугольник со сторонами 4 см и 6 см вращается вокруг большей стороны. Найти объем, площадь полной поверхности и площадь осевого сечения тела вращения.
2. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Найти объем, площадь полной поверхности, площадь осевого сечения и центральный угол развертки получившегося тела вращения.
3. Образующая конуса равна 13 см, а диаметр основания равен 24 см. Найти объём, площадь боковой поверхности и площадь осевого сечения конуса.
4. Шар и цилиндр имеют равные объёмы, а диаметр шара равен диаметру основания цилиндра. Найти радиус шара, площадь поверхности шара и объём цилиндра, если высота цилиндра равна 8 см.
5. Найти объём шарового сектора и шарового сегмента, если радиус основания сегмента равен 20 см и радиус шара равен 25 см. Ответ выразить в дм3 и округлить до десятых.
6.Высота прямого цилиндра на 8 см больше радиуса его основания. Найти объём цилиндра и площадь его осевого сечения, если площадь полной поверхности равна 48π см².
7. Прямоугольная трапеция с основаниями 5 см и 8 см и высотой 4 см вращается около большего основания. Найти объём полученного тела вращения.
8. Сколько шариков диаметром 2 см можно отлить из металлического кубика с ребром 4 см?
9. Три металлических кубика с ребром 3 см сплавлены в один шар. Найти площадь поверхности шара. Ответ округлить до сотых.
10. Равнобокая трапеция с основаниями 12 см и 28 см и высотой 6 см вращается вокруг меньшего основания. Найти объём и площадь поверхности полученного тела вращения.
Практическое занятие № 13
Круглые тела. 2 вариант
1. Прямоугольник со сторонами 5 см и 8 см вращается вокруг меньшей стороны. Найти объем, площадь полной поверхности и площадь осевого сечения тела вращения.
2. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг большего катета. Найти объем, площадь полной поверхности, площадь осевого сечения и центральный угол развертки получившегося тела вращения.
3. Образующая конуса равна 10см, а диаметр основания равен 16 см. Найти объём, площадь боковой поверхности и площадь осевого сечения конуса.
4. Шар и конус имеют равные объёмы, а диаметр шара равен диаметру основания конуса. Найти радиус шара, площадь поверхности шара и объём конуса, если высота конуса равна 12 см.
5. Найти объём шарового сектора и шарового сегмента, если радиус основания сегмента равен 24 см и радиус шара равен 26 см. Ответ выразить в дм3 и округлить до десятых.
6. Высота прямого цилиндра на 16 см больше радиуса его основания. Найти объём цилиндра и площадь его осевого сечения, если площадь полной поверхности равна 132π см².
7. Прямоугольная трапеция с основаниями 6 см и 10 см и высотой 3 см вращается около большего основания. Найти объём полученного тела вращения.
8. Сколько кубиков с ребром 2 см можно отлить из металлического шарика диаметром 6 см?
9. Четыре металлических шарика радиуса 4 см сплавлены в один куб. Найти площадь поверхности этого куба. Ответ округлить до сотых.
10. Равнобокая трапеция с основаниями 12 см и 28 см и высотой 6 см вращается вокруг меньшего основания. Найти объём и площадь поверхности полученного тела вращения.
Практическое занятие № 14
Вычисление пределов функций. Вариант 1.
Вычислить пределы
![]()
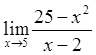
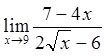
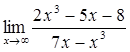
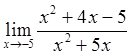
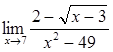
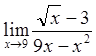
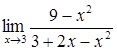
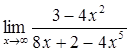
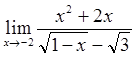
![]()
Практическое занятие № 14
Вычисление пределов функций. Вариант 2.
Вычислить пределы
![]()
![]()
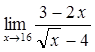
![]()
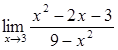
![]()
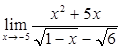
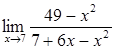
![]()
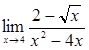
![]()
Практическое занятие № 15
Нахождение производной функции. Вариант 1.
1. Найти производные следующих функций.
А).
![]()
Б).
![]() В).
В). ![]()
Г).
![]()
2. Решить
уравнение ![]()
![]()
3. Решить
неравенство ![]()
![]()
4. Решить
неравенство ![]()
![]()
Практическое занятие № 15
Нахождение производной функции. Вариант 2.
1. Найти производные следующих функций.
А).
![]()
Б).
![]() В).
В). ![]()
Г).
![]()
2. Решить
уравнение ![]()
![]()
3. Решить
неравенство ![]()
![]()
4. Решить
неравенство ![]()
![]()
Практическое занятие № 16
Применение производной для решения задач. Вариант 1.
1. Найти производные следующих функций и вычислить
А). ![]() ,
,![]()
Б).
![]() ,
,![]() В).
В). ![]() ,
, ![]()
Г).
![]() ,
,![]()
2 . Написать уравнения А). касательной, Б). нормали, проведённых к графику данной функции в данной точке.
А). ![]() Б).
Б). ![]()
3. Найти экстремумы функции.
А). ![]() Б).
Б). ![]()
4. Найти координаты точки перегиба графика функции.
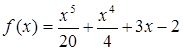 Б).
Б). ![]()
5. Тело, массой 3 кг, движется прямолинейно по закону
![]()
Найти действующую силу F и кинетическую энергию Е тела через 4 секунды после начала движения. Через сколько секунд после начала движения точка остановится? Какое расстояние точка прошла к этому моменту времени?
6. Исследовать функцию по общей схеме и построить ее график
А). ![]() Б).
Б).
![]() В).
В). ![]()
Практическое занятие № 16
Применение производной для решения задач. Вариант 2.
1. Найти производные следующих функций.
А).
![]() ,
, ![]()
Б).
![]() ,
,![]() В).
В). ![]() ,
, ![]()
Г).
![]() ,
,![]()
2. Написать уравнения А). касательной, Б). нормали, проведённых к графику данной функции в данной точке.
А). ![]() Б).
Б).![]()
3. Найти экстремумы функции.
А). ![]() Б).
Б). ![]()
4. Найти координаты точки перегиба графика функции.
![]() Б).
Б). ![]()
5. Тело, массой 4 кг, движется прямолинейно по закону
![]()
Найти действующую силу F и кинетическую энергию Е тела через 3 секунды после начала движения. Через сколько секунд после начала движения точка остановится? Какое расстояние точка прошла к этому моменту времени?
6. Исследовать функцию по общей схеме и построить ее график
А). ![]() Б).
Б).
![]() В).
В). ![]()
Практическое занятие № 17
Определенный интеграл и его применение. Вариант 1.
1. Проверить, является ли функция F(x) первообразной для функции f(x)
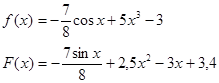
2. Для функции f(x)=16x3-3 найти ту первообразную, график которой проходит через точку М (-1; 5)? Проходит ли график найденной первообразной через точку N (2; -9)?
Сравнить F(-3) и F(1).
3. Вычислить определённые интегралы:
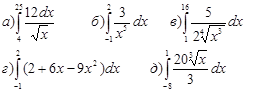
4. Вычислить площадь фигуры, ограниченной линиями:
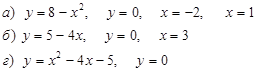
Практическое занятие № 17
Определенный интеграл и его применение. Вариант 2.
1. Проверить, является ли функция F(x) первообразной для функции f(x)
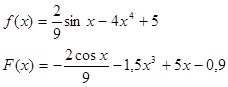
2. Для функции f(x)=8x3-3 найти ту первообразную, график которой проходит через точку М (-1;- 5)?
Проходит ли график найденной первообразной через точку N (2; 7)?
Сравнить F(-2) и F(3).
3. Вычислить определённые интегралы:
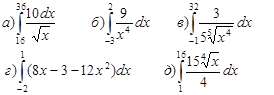
4. Вычислить площадь фигуры, ограниченной линиями:
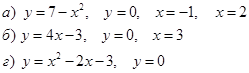
Практическое занятие № 18
Классическое определение вероятности. Вариант 1.
![]()
4. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
5. Контролер, проверяя качество 500 изделий, установил, что 10 из них относятся ко второму сорту, а остальные - к первому. Найдите вероятность выбора изделия второго сорта.
6. В коробке лежат 200 белых, 100 красных и 50 зеленых шаров. Наудачу вынимается один шар. Чему равны вероятности получить шар белого, красного или зеленого цвета?
7. Наташа купила лотерейный билет, который участвует в розыгрыше 100 призов на 50000 билетов, а Лена – билет, который участвует в розыгрыше трех призов на 70000. У кого больше шансов выиграть?
8. Из коробки, в которой осталось 5 конфет с фруктовой начинкой и 3 - с начинкой пралине, достают одну конфету. Какова вероятность, что она будет с начинкой пралине?
9. В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и наудачу извлекается одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой.
Практическое занятие № 18
Классическое определение вероятности. Вариант 2.
![]()
4. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным.
5. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
6. Лотерея состоит из 1000 билетов, среди них 200 выигрышных. Наугад вынимается один билет из 1000. Чему равна вероятность того, что этот билет выигрышный?
7. Бросается игральная кость. Чему равны вероятности следующих событий: А={выпала грань с 6 очками}, В={выпала грань с четным числом очков}, С={выпала грань с числом очков, делящимся на 3}?
8. В коробке лежат 10 одинаковых шаров, на каждом из которых написан его номер от 1 до 10. Найдите вероятность следующих событий: а) извлекли шар № 7; б) номер извлеченного шара – четное число; в) номер извлеченного шара кратен 3.
9. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит а) цифры 1, б) цифры 0.
Практическое занятие № 19
Числовые характеристики случайной величины. Вариант 1.
1. Известны
математические ожидания двух случайных величин ![]() и
и ![]() :
:![]() Найти
математическое ожидание величины
Найти
математическое ожидание величины ![]()
2. Закон распределения случайной величины имеет вид:
|
|
0 |
1 |
2 |
|
|
0,0625 |
0,375 |
0,5625 |
Найти математическое ожидание и дисперсию случайной величины.
3. В результате 10 измерений веса тела получены значения: 15, 16, 15, 14, 16, 16, 16, 15, 15, 13. Оценить математическое ожидание и дисперсию веса тела.
4. Найти математическое ожидание числа очков, выпадающих при бросании игральной кости.
5. Дискретная случайная
величина ![]() имеет закон распределения
имеет закон распределения
|
|
0 |
1 |
2 |
|
|
0,3 |
0,5 |
0,2 |
Найти дисперсию и среднее квадратичное отклонение случайной величины.
6. Случайная величина Х задана законом распределения. Найти p3 и р2. Построить многоугольник распределения. Найти все числовые характеристики этой случайной величины.
|
Х |
2 |
4 |
5 |
6 |
|
Б) |
Х |
10 |
15 |
20 |
|
р |
0,3 |
0,1 |
|
0,4 |
|
|
р |
0,1 |
|
0,2 |
Практическое занятие № 19
Числовые характеристики случайной величины. Вариант 2.
1. Известны
математические ожидания двух независимых величин ![]() и
и ![]() :
:![]() Найти
математическое ожидание величины
Найти
математическое ожидание величины ![]()
2. Необходимо оценить математическое ожидание и дисперсию по полученной выборке,закон распределения случайной величины имеет вид:
|
|
-0,04 |
0,06 |
0,03 |
|
|
0,6 |
0,4 |
0,2 |
3. В результате измерения
заряда ![]() некоторого тела в серии из 11
опытов получены следующие результаты:
некоторого тела в серии из 11
опытов получены следующие результаты:
|
|
7,28 |
7,30 |
7,31 |
7,33 |
|
|
2 |
4 |
3 |
2 |
Найти математическое ожидание и дисперсию случайной величины.
4. Найдите математическое ожидание дискретной случайной величины, закон распределения которой задан таблицей
|
|
3 |
4 |
5 |
6 |
7 |
|
|
0,1 |
0,2 |
0,4 |
0,2 |
0,1 |
5. Найдите дисперсию
дискретной случайной величины ![]() и ее среднее квадратичное
отклонение – числа очков выпадающих при подбрасывании игральной кости.
и ее среднее квадратичное
отклонение – числа очков выпадающих при подбрасывании игральной кости.
6. Случайная величина Х задана законом распределения. Найти p3 и р1. Построить многоугольник распределения. Найти все числовые характеристики этой случайной величины.
|
Х |
3 |
5 |
6 |
7 |
|
Б) |
Х |
10 |
12 |
15 |
|
р |
0,2 |
0,1 |
|
0,4 |
|
|
р |
|
0,3 |
0,5 |
Практическое занятие № 20
Решение уравнений и неравенств. Вариант 1.
1. Решить уравнения.
![]()
![]()
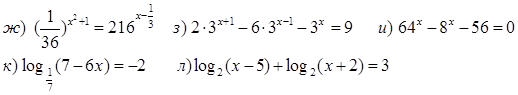
м) ![]()
н) ![]() о)
о)![]()
2. Решить неравенства.
![]()
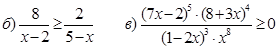
![]()
![]()
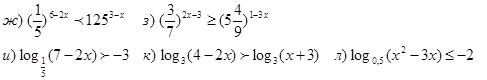
4. Изобразить множество решений систем неравенств:
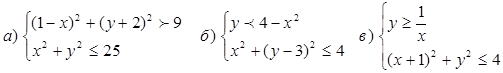
Практическое занятие № 20
Решение уравнений и неравенств. Вариант 2.
1. Решить уравнения.
![]()
![]()
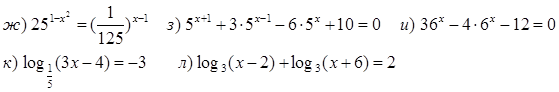
м) ![]()
н) ![]() о)
о)![]()
2. Решить неравенства.
![]()
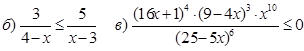
![]()
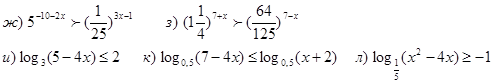
4. Изобразить множество решений систем неравенств:
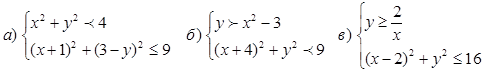
3. КОНТРОЛЬНЫЕ РАБОТЫ
Контрольная работа № 1
Корни, степени и логарифмы. Вариант 1.
1. Вычислить значение выражения.
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
2. Решить иррациональные уравнения.
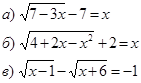
3. Решить показательные уравнения.
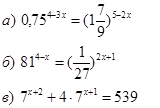
4. Решить логарифмические уравнения.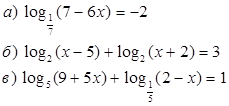
Контрольная работа № 1
Корни, степени и логарифмы. Вариант 2.
1. Вычислить значение выражения.
![]()
![]()
![]()
![]() ,
,
![]()
![]()
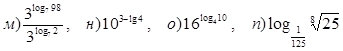
2. Решить иррациональные уравнения.
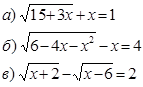
3. Решить показательные уравнения.
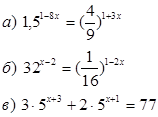
4. Решить логарифмические уравнения.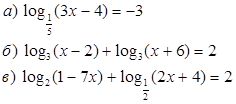
Контрольная работа № 2
Основы тригонометрии. Вариант 1.
1. Перевести углы из радиан в градусы и наоборот, определить четверть.
![]()
2. Упростить выражение по формулам приведения
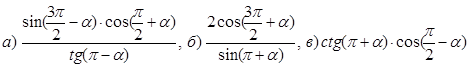
![]()
Найти
![]()
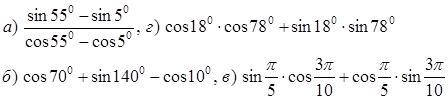
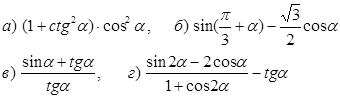
7. Построить график функции у = sinx и перечислить свойства функции.
8. Решить тригонометрические уравнения и найти частные решения при данном значении k
А).
![]()
Б).
![]()
В).
![]()
Г).
![]()
9. Решить тригонометрическое уравнение
А).![]()
Б).
![]()
Контрольная работа № 2
Основы тригонометрии. Вариант 2.
1. Перевести углы из радиан в градусы и наоборот, определить четверть.
![]()
2. Упростить выражение по формулам приведения
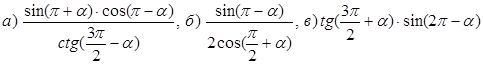
![]()
Найти
![]()
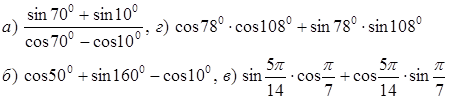

7. Построить график функции у = cosx и перечислить свойства функции.
8. Решить тригонометрические уравнения и найти частные решения при данном значении k
А).
![]()
Б).
![]()
В).
![]()
Г).
![]()
9. Решить тригонометрическое уравнение
А).
![]()
Б).
![]()
Контрольная работа № 3
Многогранники и круглые тела. Вариант 1.
1. В прямой треугольной призме все ребра равны. Боковая поверхность равна 75 м2 . Найти высоту призмы.
2. Боковая поверхность правильной четырехугольной призмы равна 64 м2, а полная поверхность равна 128 м2 . Найти боковое ребро призмы.
3. В прямой треугольной призме стороны основания равны 37; 13; 40, а полная поверхность 1380. Найти боковую поверхность и высоту призмы.
4. В наклонной треугольной призме боковое ребро равно 8 см; стороны перпендикулярного сечения 36 см; 24 см; 31 см. Найти боковую поверхность призмы.
5. По стороне основания а и боковому ребру в определить объем правильной треугольной пирамиды, если: а = 10 см, в = 12см.
6. В правильной четырехугольной пирамиде Н = Зм, в = 5м (боковое ребро). Найти объем .
7. Боковое ребро правильной четырехугольной пирамиды (усеченной) равно Зм, стороны основания 5м и 1м. Найти объем.
8. Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 900. Найдите площадь сечения, если высота цилиндра равна 6 см, а расстояние между осью цилиндра и секущей плоскостью равно 3 см.
9. Высота конуса равна 6 см, а образующая наклонена к плоскости основания под углом 300. Найдите площадь сечения конуса плоскостью, проходящей через две образующие, угол между которыми 600.
10. Площадь сечения шара плоскостью, проходящей через его центр, равна 16π см2. Найдите площадь сферы.
11. Каждое ребро правильного тетраэдра равно 6 см. Найдите объемы тетраэдра и вписанного в него конуса.
12. Диагональ правильной четырехугольной призмы равна 4 см и составляет с плоскостью боковой грани угол 300. Найдите объемы призмы и описанного около нее цилиндра.
Контрольная работа № 3
Многогранники и круглые тела. Вариант 2.
1. В прямой треугольной призме все ребра равны. Боковая поверхность равна 243 м2. Найти высоту призмы.
2. Боковая поверхность правильной четырехугольной призмы равна 200 м , а полная поверхность равна 300 м . Найти боковое ребро призмы.
3. В прямой треугольной призме стороны основания равны 9; 10; 17, а полная поверхность 216 . Найти боковую поверхность и высоту призмы.
4. В наклонной треугольной призме боковое ребро равно 8 см; стороны перпендикулярного сечения 40 см; 32 см; 29 см . Найти боковую поверхность призмы
5. По стороне основания а и боковому ребру в определить объем правильной четырехугольной пирамиды, если: а = 8 см, в = 10см.
6. В правильной треугольной пирамиде Н = 4м, в = 5м. Найти объем.
7. Боковое ребро правильной треугольной пирамиды (усеченной) равно Зм, стороны основания 5м и 1м. Найти объем
Контрольная работа № 4
Начала математического анализа. Вариант 1.
1.
Составьте
уравнение касательной к графику функции ![]() в точке
в точке ![]()
2.
Составьте
уравнения касательных к графику функции ![]()
в точках его пересечения с осью абсцисс. Найдите точку пересечения этих касательных.
3.
Исследуйте
функцию ![]() на монотонность и экстремумы и постройте ее график.
на монотонность и экстремумы и постройте ее график.
а) ![]() на
отрезке
на
отрезке ![]() ;
;
б) ![]() на
отрезке
на
отрезке ![]() .
.
5.
Докажите, что
функция ![]() является первообразной для
является первообразной для
функции
![]() .
.
6.
Для данной
функции ![]() найдите ту первообразную, график
найдите ту первообразную, график
которой
проходит через заданную точку ![]() .
.
7.
Вычислите
интеграл: а) ![]() ; б)
; б) 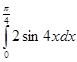 .
.
8.
Вычислите
площадь фигуры, ограниченной линиями ![]()
Контрольная работа № 4
Начала математического анализа. Вариант 2.
1.
Составьте
уравнение касательной к графику функции ![]() в точке
в точке ![]()
2.
Составьте уравнения
касательных к графику функции ![]()
в точках его пересечения с осью абсцисс.
и постройте ее график.
а) ![]() на
отрезке
на
отрезке ![]() ;
;
б) ![]() на
отрезке
на
отрезке ![]() .
.
первообразной
для функции ![]() .
.
6.
Для данной
функции ![]() найдите ту первообразную,
найдите ту первообразную,
график
которой проходит через заданную точку ![]() .
.
7.
Вычислите
интеграл: а) ![]() ; б)
; б) 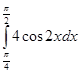 .
.
8.
Вычислите
площадь фигуры, ограниченной линиями ![]()
Контрольная работа № 5
Итоговая. Вариант 1.
При выполнении заданий № 1-2 соотнесите содержание столбца 1 с содержанием столбца 2.
|
№ п/п |
Понятие |
Определение |
|
1. |
а) Корень n-степени из числа а б) Арифметический корень n-степени из числа а в)
Степень числа
|
1) Неотрицательное число, n-степень которого равна а
2) Число
3 Число, n-степень которого равна а |
|
2. |
а)
Функция называется чётной б)
Функции называется нечётной |
1)Если
для любого
2)
Если для любого х из области определения |
При выполнении заданий № 3-25 выберите букву, соответствующую правильному варианту ответа
|
3. |
Значение выражения |
а).15; б).60; в).30; г).18.
|
|
4. |
Область определения функции у =
|
а). в). |
|
5. |
Решением
неравенства |
а). (- в). (2;+ |
|
6.
|
График
функции, заданной формулой |
|
|
7. |
Решением
уравнения |
а) .0; б).0,-3; в)-3; г) 3. |
|
8. |
Значение
выражения |
а) 8; б) 12; в) 6; г) 5. |
|
9. |
Промежуток,
которому принадлежит корень уравнения |
а) (-2;4); б) (0;-2); в) |
|
10 |
После приведения к функции угла |
а)-cos в) -sin |
|
11 |
Значение
cos
|
а) - |
|
12 |
Наименьший корень уравнения
|
а)0; б) в) -1; г) 1. |
|
13 |
Производная функции
|
а) в) |
|
14
|
Минимум
функции равен |
а) 7; б) -7;
в) 9; г)-9.
|
|
15 |
Наименьшее значение функции У = 4 +
х |
а) 4; б) -5; в) 3; г)-3. |
|
16 |
Площадь
фигуры, ограниченной линиями
|
а) в) 36; г) 30. |
|
17 |
Точка |
а) (-3;5;-1); б) (5;5;1);
в) (5;3;1); г) (-5;3;-1)
|
|
18. |
Множество всех первообразных функции
имеет вид
|
а). F(x) = cos x +2x; б) F(x) = -cosx +2x +c; в)F(x) = -cosx
+2x -4; г) F(x) = cosx + |
|
19. |
V правильной пирамиды равен |
а) в) |
|
20. |
Значения
|
а) |
|
21. |
Областью определения логарифмической функции является |
а) (0; в) (- |
|
22. |
Значение
|
а)
12; б) в) |
|
23. |
Точка М
находится на расстоянии 10см от каждой стороны квадрата, площадь которого
равна 64 |
а) в) 16см; г) другой вариант.
|
|
24. |
Критическими
точками функции являются точки |
а) в) x =0; г) |
|
25.
|
S боковой поверхности цилиндраравна
|
а) в) |
Контрольная работа № 5
Итоговая. Вариант 2.
При выполнении заданий № 1-2 соотнесите содержание столбца 1 с содержанием столбца 2.
|
№ п/п |
Понятие |
Определение |
|
1. |
а) Функция f возрастает на множестве P
б) Функция f убывает на множестве P
в) Точка
х |
1) Если
для любых х выполнено
неравенство f( х
2) Если
для всех х из некоторой окрестности х неравенство
f (x) 3) Если
для любых х выполнено
неравенство f( х |
|
2. |
а) График чётной функции
б) График нечётной функции |
1) Симметричен относительно начала координат
2) Симметричен относительно оси ординат |
При выполнении заданий № 3-25 выберите букву, соответствующую правильному варианту ответа
|
3. |
Значение выражения
|
а) 21; б) 3,5; в) 13; г) 2,1. |
|
|
4. |
Область определения функции у = |
а) в) |
|
|
5. |
Решением
неравенства является промежуток |
а) (
в) (1; |
|
|
6. |
Значение
выражения |
а) 2; б) 0,5; в)
3; г) log |
|
|
7.
|
График
функции, заданной формулой |
|
|
|
8. |
Решением уравнения
|
а) 2; б) -1;
в) 9; г) 0. |
|
|
9. |
Решением
уравнения является число |
а) 8; б)0,8;
в) 0; г) 3. |
|
|
10. |
После
приведения к функции угла |
а) -cos
в) -sin
|
|
|
11. |
Значение
ctg |
а) |
|
|
12. |
Промежуток,
которому принадлежит корень уравнения |
а) (6;8); б) (2;4);
в) (4;6); г) (0;2).
|
|
|
13. |
Производная функции y = tgx +2 sinx имеет вид |
а).
в) |
|
|
14. |
Максимум
функции |
а) 2; б) -2;
в)-6; г)-6. |
|
|
15. |
Наибольшее
значение функции f(x) = 4 |
а) -5; б) -3;
в)-4; г) 5. |
|
|
16. |
Множество всех первообразных функции
имеет вид |
а) F(x)=-sinx+ б) F(x)=sinx+ в) F(x) =sinx + г) F(x) =- sinx + |
|
|
17. |
Площадь
фигуры, ограниченной линиями у = 1 |
а)
|
|
|
18 |
Площадь боковой поверхности правильной пирамиды равна
|
а) в) |
|
|
19 |
|
а) в) - |
|
|
20. |
Продолжите формулу
|
а) б) в) г) |
|
|
21. |
Областью определения показательной функции является |
а) (0; в) (- |
|
|
22. |
Длина
отрезка, соединяющего точки |
а) в)
3; г) |
|
|
23. |
Критическими
точками функции являются точки
|
а)
в) x =
-1; г) |
|
|
24.
|
Векторы |
а) 5;4 б) 1;2
в) 2;1 г) 2;6. |
|
|
25. |
Объем цилиндра с радиусом 3м и высотой 3м равен… |
а) 16
в) |
|
Контрольная работа № 5
Итоговая. Вариант 3.
При выполнении заданий № 1-2 соотнесите содержание столбца 1 с содержанием столбца 2.
|
№ п/п |
Понятие |
Определение |
|
1. |
а) Сечение пирамиды плоскостью, перпендикулярной основанию и проходящей через вершину б) Сечение цилиндра плоскостью, параллельной высоте |
1) Прямоугольник.
2) Треугольник.
3) трапеция. |
|
2. |
а) Если
при переходе через точку х б) Если
при переходе через точку х |
1) х
2) х
|
При выполнении заданий 3-25 выберите букву, соответствующую правильному варианту ответа
|
3. |
Значение
выражения равно |
а) 6; б) 12;
в) 10; г).18. |
|
|
4. |
Область определения функции у = |
а) в) |
|
|
5. |
Решением
неравенства |
а). (
в). (-3;
|
|
|
6. |
Значение выражения
|
а). 10; б). 9;
в). 4; г). 0. |
|
|
7.
|
График
функции, заданной формулой |
|
|
|
8. |
Решением
уравнения является число |
а).-2; б).-2,3;
в).-3 г). 3. |
|
|
9. |
Значение выражения sin 62 равно |
а) |
|
|
10. |
После приведения к функции угла |
а) -cos
в) -sin |
|
|
11. |
Значение
cos
|
а) |
|
|
12. |
Промежуток, которому принадлежит корень уравнения
|
а) (6;8); б) (2;4);
в) (4;6); г) (0;2).
|
|
|
13. |
Решением уравнения
|
а) 1; б) -1;
в) 0; г) 2. |
|
|
14 |
Производная
функции |
а). б). в). г) |
|
|
15 |
Наибольшее
значение функции f(x) = 4 |
а) -5; б) -3; в)-4; г) 5. |
|
|
16 |
Множество всех первообразных функции
имеет вид |
а) F(x)=-sinx+ б) F(x)=sinx+ в) F(x) =sinx +
г) F(x) =- sinx + |
|
|
17 |
Площадь
фигуры, ограниченной линиями у = 1
|
а) |
|
|
18 |
Площадь боковой поверхности правильной пирамиды равна |
а) в) |
|
|
19 |
|
а) в) - |
|
|
20. |
Продолжите формулу
|
а) б) в) г) |
|
|
21. |
Областью определения показательной функции является |
а) (0;
в) (- |
|
|
22. |
Длина
отрезка, соединяющего точки |
а)
в)
3; г) |
|
|
23. |
Критическими
точками функции являются точки |
а)
в) x =
-1; г) |
|
|
24.
|
Векторы |
а) 5;4 б) 1;2
в) 2;1 г) 2;6. |
|
|
25. |
Объем цилиндра с радиусом 3м и высотой 3м равен… |
а) 16
в) |
|
Контрольная работа № 5
Итоговая. Вариант 4.
При выполнении заданий № 1-2 соотнесите содержание столбца 1 с содержанием столбца 2.
|
№ п/п |
Понятие |
Определение |
|
1. |
а) При а
б) При у = в) Логарифмическая функция при а |
1)Возрастает
на промежутке
2) Возрастает на множестве всех действительных чисел
3) Убывает на множестве всех действительных чисел |
|
2. |
а) Если б) Если интервала |
1) то
функция
2) то
функция |
При выполнении заданий № 3-25 выберите букву, соответствующую правильному варианту ответа
|
3. |
Значение выражения
|
а).2 в).
0; г).- |
|
4. |
Область определения функции у = |
а) в). |
|
5. |
Решением
неравенства |
а). (- в).
[-3;+ |
|
6. |
Значение выражения
|
а).
в).
|
|
7.
|
График
функции, заданной формулой |
|
|
8. |
Решением уравнения
число |
а). -2; б).-5,2;
в) .2; г). -5. |
|
9. |
Значение выражения cos 64 равно |
а). в).- |
|
10. |
После приведения к функции угла |
а). cos
в). sin |
|
11. |
Значение
tg 7
|
а). - в). - |
|
12. |
Решением уравнения
|
а). -1; б). 1;
в). 2; г).0. |
|
13. |
Промежуток, которому принадлежит корень уравнения
|
а).
(1;3); б).
в). (0;1);г). (1;2). |
|
14. |
Тангенс
угла наклона касательной |
а). -2; б). 2;
в). 1; г). 1. |
|
15. |
Минимум
функции равен |
а).-3; б).3;
в). 0; г).-4. |
|
16. |
Общий
вид первообразных F(x) для функции
|
а).
в). |
|
17. |
Площадь фигуры, ограниченной графиком функции у = 4 -
|
а) в). |
|
18. |
Значение
(значения) к, при котором векторы |
а). 2; б). 4;
в). 4;2; г). 0; 6. |
|
19. |
Продолжите формулу соs (
|
а). б). в). г). |
|
20. |
Площадь сферы равна
|
а). в). |
|
21. |
Выберите нечётную функцию
|
а). у в). y =tgx ; г). y = |
|
22. |
Областью значения функции y = sinx
|
а). (-1; в). (- |
|
23.
|
Значение
|
а). в). |
|
24. |
Критическими
точками функции являются точки |
а). в). |
|
25.
|
Объём цилиндра равен
|
а). в). |
4.ТЕСТЫ
Тест №1 по теме «Комплексные числа»
1. В какой из строк записаны чисто мнимые числа?
1. z = -2; 2. z = -2i; 3. z = 4-2i; 4. z = 3,2i.
2. Каждому комплексному числу z=a+bi можно поставить в соответствие точку с координатами
1. (a2; b); 2. (-a; -b); 3. (a; b); 4. (a; bi).
3. Что означает фраза «Число z принадлежит первой координатной четверти»?
1. действительная и мнимая часть положительны;
2. действительная и мнимая часть отрицательны;
3. действительная часть положительна, а мнимая часть отрицательна;
4. действительная часть отрицательна, а мнимая часть положительна.
4. Геометрически операция сопряжения есть…
1. осевая симметрия относительно оси Оу;
2. осевая симметрия относительно оси Ох;
3. центральная симметрия относительно начала координат;
4. параллельный перенос на вектор i.
5. Укажите номера верных утверждений.
1. Если у комплексного числа сохранить мнимую часть и поменять знак у действительной, то получится комплексное число, противоположное данному.
2. Если у комплексного числа сохранить действительную часть и поменять знак у мнимой, то получится комплексное число, сопряженное данному.
3.
Чтобы найти
частное ![]() необходимо числитель и знаменатель
дроби умножить на число, сопряженное знаменателю.
необходимо числитель и знаменатель
дроби умножить на число, сопряженное знаменателю.
4. Геометрической моделью множества С является координатная плоскость.
6. Если комплексное число z задано в виде z = 6 + 9i, то число 9 называют:
1. действительной частью z;
2. мнимой частью z;
3. мнимой единицей;
4. аргументом числа z.
7. Как называется число i?
1. несуществующая единица;
2. необыкновенная единица;
3. мнимая единица;
4. искусственная единица.
8. Выберете номера верных равенств.
1. i= ![]() ; 2. i = -1; 3. i=
; 2. i = -1; 3. i= ![]() ; 4. i2 = -1
; 4. i2 = -1
9. Запись вида z = a + bi называют
1. алгебраической формой;
2. тригонометрической формой;
3. векторной формой;
4. геометрической формой.
10. Выберете верные утверждения
1.
R⊂C; 2. R = Q∪ Z; 3. C = Q∪![]() ; 4. Q∩
; 4. Q∩![]() = ∅.
= ∅.
Тест №2 по теме «Прямые и плоскости в пространстве»
1. Сколько прямых можно провести через одну точку пространства?
1) Ни одной. 2) Одну. 3) Две . 4) Бесконечно много.
2. Сколько плоскостей можно провести через одну точку пространства?
1) Ни одной. 2) Одну . 3) Две. 4) Бесконечно много.
3. Сколько прямых можно провести через две точки пространства?
1) Ни одной. 2) Одну. 3) Две. 4) Бесконечно много.
4. Сколько плоскостей можно провести через две точки пространства?
1) Ни одной. 2) Одну. 3) Две. 4) Бесконечно много.
5. Сколько прямых можно провести через различные пары из трех точек пространства, не принадлежащих одной прямой?
1) Ни одной. 2) Три. 3) Шесть. 4) Бесконечно много.
6. Сколько плоскостей можно провести через три точки пространства, не принадлежащие одной прямой?
1) Ни одной. 2) Одну. 3) Три. 4) Бесконечно много.
7. Сколько плоскостей можно провести через три точки пространства, принадлежащие одной прямой?
1) Ни одной. 2) Одну. 3) Три. 4) Бесконечно много.
8. Сколько общих точек имеют две пересекающиеся плоскости?
1) Одну. 2) Две. 3) Три. 4) Бесконечно много.
9. Какое наибольшее число прямых можно провести через различные пары четырех точек пространства?
1) Четыре. 2) Пять. 3) Шесть. 4) Восемь.
10. Какое наибольшее число прямых можно провести через различные пары из пяти точек пространства?
1) 5. 2) 10. 3) 15. 4) 25.
Тест №3 по теме «Основы стереометрии»
1. Стереометрия – это:
А. раздел геометрии, в котором изучаются фигуры в пространстве;
Б. наука о свойствах геометрических фигур;
В. раздел геометрии, в котором изучаются фигуры на плоскости;
Г. наука о свойствах треугольников.
2. Основными фигурами в пространстве являются
А. окружность Б. точка В. прямая Г. плоскость
3. Какая из трех аксиом не относится к аксиомам стереометрии:
А. какова бы ни была плоскость, существуют точки, принадлежащая этой плоскости, и точки, не принадлежащие ей;
Б. если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну;
В. через две точки можно провести прямую и притом только одну;
Г. если две различные плоскости имеют общую точку, то они пересекаются по прямой.
4. Если две прямые лежат в одной плоскости и не пересекаются, то они называются
А. скрещивающимися Б. параллельными
В. накрест лежащими Г. перпендикулярными
5. Какого варианта взаимного расположения прямой и плоскости не существует?
А. прямая параллельна плоскости Б. прямая перпендикулярна плоскости
В. прямая лежит на плоскости Г. все варианты существуют
6. Если прямая и плоскость не пересекаются, то они называются
А. скрещивающимися Б. перпендикулярными
В. параллельными Г. таких не существует
7. Две прямые перпендикулярны одной плоскости. Какое их взаимное расположение?
А. не лежат в одной плоскости Б. пересекаются В. перпендикулярны Г. параллельны
8. Если две прямые не лежат в одной плоскости, то они называются
А. скрещивающимися Б. параллельными В. накрест лежащими Г. перпендикулярными
9. Из точки А параллелограмма АВСМ восстановлен перпендикуляр АК. Какое взаимное расположение прямых АК и СМ?
А. скрещивающиеся Б. параллельны В. перпендикулярны Г. пересекаются
10. Две прямые на плоскости называются перпендикулярными, если
А. они пересекаются под прямым углом Б. они не пересекаются
В. они пересекаются под углом меньше ![]() Г. затрудняюсь ответить
Г. затрудняюсь ответить
11. Если прямая перпендикулярна плоскости, то она перпендикулярна
А. одной прямой этой плоскости Б. двум прямым этой плоскости
В. каждой прямой этой плоскости Г. ни одной прямой этой плоскости
12. Перпендикуляр – это
А. отрезок, соединяющий данную точку с точкой плоскости
Б. отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости
В. отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, параллельной плоскости
Г затрудняюсь ответить
13. Проекцией наклонной называется
А. основание наклонной
Б. отрезок, соединяющий основание перпендикуляра и наклонной, проведенных из одной и той же точки
В. отрезок, соединяющий основание перпендикуляра и наклонной, проведенных из разных точек плоскости
Г. затрудняюсь ответить
14. Наклонная – это
А. отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости
Б. любой отрезок, соединяющий данную точку с точкой плоскости
В. отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, параллельной плоскости
Г. затрудняюсь ответить
15. Наклонная, перпендикуляр и проекция наклонной образуют
А. равносторонний треугольник Б. равнобедренный треугольник
В. остроугольный треугольник Г. прямоугольный треугольник
16. Сколько точек пересечения с плоскостью имеет наклонная?
А. 1 Б. 2 В. 4 Г. 0
17. У равных наклонных
А. параллельные проекции Б. равные проекции
В. перпендикулярные проекции Г. нет правильного ответа
18. Сколько наклонных можно провести через заданную точку пространства к плоскости?
А. 1 Б. 2 В. 3 Г. много
19. Сколько плоскостей можно провести через наклонную и ее проекцию?
А. Множество Б. 3 В. 2 Г. 1
20. Расстояние между точками ![]() и
и ![]() вычисляется
по формуле
вычисляется
по формуле
А. ![]() Б.
Б.
![]()
В. ![]() Г. затрудняюсь
ответить
Г. затрудняюсь
ответить
21. Углом между прямой и плоскостью называется
А. угол между этой прямой и ее проекцией на плоскость
Б. угол между этой прямой и перпендикуляром, опущенным из любой точки прямой
В. прямой угол
Г. затрудняюсь ответить
22. Прямая, поведенная в плоскости перпендикулярно проекции наклонной, перпендикулярна…
А. любой прямой лежащей в плоскости Б. наклонной
В. любой прямой пересекающей плоскость Г. нет правильного ответа
Тест №4 по теме «Векторы в пространстве»
1. Вектор – это …
2. Вектор в пространстве задаётся …
3. Чтобы найти координаты вектора, надо …
4. Любой вектор имеет определённую …
5.
Если ![]() (а1, а2, а3), то
(а1, а2, а3), то ![]() =…
=…
6. Два вектора называются равными, если…
7. Равные векторы имеют …
8. Если отложить равные векторы от одной точки, то
9. Разностью векторов является …
10. Разность равных векторов равна …
11. Два вектора называются коллинеарными, если …
12. Векторы называются сонаправленными, если …
13. Если отложить сонаправленные векторы от одной точки, то
14. Если отношения соответственные координаты двух векторов равны одному и тому же отрицательному числу, то векторы…
15. Произведением вектора на число является…
16. Если скалярное произведение векторов равно 0, то…
17. Если векторы противоположно направлены, то их скалярное произведение равно…
18.
Вектор ![]() , его умножили на число -3, получили вектор
, его умножили на число -3, получили вектор ![]() .Какими будут векторы
.Какими будут векторы ![]() и
и
![]() ?
?
19. Два вектора называются противоположными, если…
20. Противоположные векторы имеют …
21. Если отложить противоположные векторы от одной точки, то
22. Суммой векторов является …
23. Сумма противоположных векторов равна …
24. Векторы называются противоположно направленными, если …
25. Если отложить противоположно направленные векторы от одной точки, то
26. Если скалярное произведение векторов не равно 0, то…
27. Если векторы сонаправлены, то их скалярное произведение равно…
28.
Вектор ![]() , его умножили на число 5, получили
вектор
, его умножили на число 5, получили
вектор ![]() .Какими будут векторы
.Какими будут векторы ![]() и
и ![]() ?
?
Тест №5 по теме «Основы тригонометрии»
1. Областью определения функции y = sin x является:
А) R; Б) ![]() ; В) х≠0; Г) (-1; 1)
; В) х≠0; Г) (-1; 1)
2. Функция y = sin x принимает отрицательные значения в:
А) I и III четв; Б) I и II четв; В) III и IV четв; Г) II и III четв.
3. Наименьший положительный период функции y = sin x
А) π; Б) 2π; В) π/2; Г) 4π
4. Четной тригонометрической функцией является функция:
А) y = sin x; Б) y = tg x; В) y = ctg x; Г) y = cos x
5. Множеством значений функции y = sin x является:
А) R; Б) у≠0; В) (-1; 1); Г) ![]()
6. Сколько точек пересечения имеет график функции y = sin x с осью Ох:
А) ни одной; Б) одну; В) две; Г) бесконечное множество.
7. Областью определения функции y = tg x является:
А) R; Б) (0; 2πn); В) х ≠ π/2 + πn; Г) (-πn/2; πn/2)
8. Функция y = tg x принимает положительные значения в:
А) I и III четв; Б) I и II четв; В) III и IV четв; Г) II и III четв.
9. Наименьший положительный период функции y = tg x
А) 4π; Б) 2π; В) π/2; Г) π.
10. Функция y = tg x является:
А) четной; Б) нечетной; В) ни четной, ни нечетной; Г) постоянной.
11. Множеством значений функции y = tg x является:
А) R; Б) у≠0; В) (-1; 1); Г) ![]()
12. Сколько точек пересечения имеет график функции y = tg x с осью Ох:
А) ни одной; Б) одну; В) бесконечное множество; Г) две.
13. Упростить по формулам
приведения sin (![]() )
)
А) cos x; Б) sin x; В) -sin x; Г) -cos x
14. Угол 1350 принадлежит:
А) I четв; Б) II четв; В) III четв; Г) IV четв.
15. Угол 4π/3 принадлежит:
А) I четв; Б) II четв; В) III четв; Г) IV четв.
16. Основное тригонометрическое тождество:
А) sin x + cos x = 1; Б) sin 2x - cos2 x = 1; В) sin x - cos x = 1; Г) sin 2x + cos2 x = 1.
17. Чему равен угол π радиан?
А) 900; Б) 1800; В) 3600; Г) 2700
18.Чему равно значение tga · ctga
А) 0; Б) 2; В) -1; Г) 1
19. Упростить по формулам
приведения ctg (![]() )
)
А) ctg x; Б) tg x; В) -ctg x; Г) -tg x
Тест №6 по теме «Функция, ее свойства и график»
1. Функцией называется зависимость переменной Y от переменной Х, при которой…
а) … каждому значению Y соответствует единственное значение Х;
б) … каждому значению Х соответствует единственное значение Y;
в) … каждому значению Х соответствует единственное значение Y и обратно.
2. Функцией называется монотонно возрастающей на данном числовом промежутке, если…
а) … большему значению аргумента соответствует меньшее значение функции;
б) … большему значению аргумента соответствует большее значение функции;
в) … меньшему значению аргумента соответствует меньшее значение функции.
3. Все значения, которые принимает независимая переменная Х образуют:
а) множество значений функции;
б) область определения функции;
в) способы задания функции.
4. Функция ![]() задана:
задана:
а) графически; б) рекуррентно; в) аналитически.
5. График какой функции получается смещением графика функции у = f(х) на «а» единиц вправо вдоль оси Ох:
а) у = f(х+а); б) у = f(х–а); в) у = f(х)+ а.
6. Если на всей области определения функции выполняется условие:
f(– x) = –f(x), то функция называется…
а) чётной;
б) нечётной;
в) ни чётной, ни нечётной.
7. Графики взаимно-обратных функций симметричны относительно:
а) начала координат;
б) оси ординат;
в) прямой у = х.
8. Все значения, которые принимает зависимая переменная Y образуют:
а) область определения функции;
б) множество значений функции;
в) промежуток возрастания функции.
9. График функции у=f(x)±b получается смещением графика функции у=f(x)
а) по оси Оу на b единиц вверх при b0 или вниз при b
б) по оси Ох на b единиц влево при b0 или вправо при b
в) по оси Оу на b единиц вниз при b0 или вверх при b
10. Функция у = f(x) называется чётной на всей области определения, если для любого х Î D (у) справедливо условие:
а) f(– x) = f(x);
б) f(– x) = –f(x);
в) f(– x) ≠ f(x) и f(– x) ≠ –f(x).
11. Функцией называется обратимой, если для неё существует обратная, т.е., если …
а) … каждому значению Y соответствует единственное значение Х;
б) … каждому значению Х соответствует единственное значение Y;
в) … каждому значению Х соответствует единственное значение Y и обратно.
12. Функцией называется монотонно убывающей на данном числовом промежутке, если…
а) … большему значению аргумента соответствует меньшее значение функции;
б) … большему значению аргумента соответствует большее значение функции;
в) … меньшему значению аргумента соответствует меньшее значение функции.
13. График нечётной функции симметричен относительно:
а) оси Оу;
б) оси Ох;
в) начала координат.
14. Функция y=f(x) называется ограниченной снизу на D(f), если
а) все значения этой функции меньше некоторого числа;
б) все значения этой функции больше некоторого числа;
в) все значения этой функции равны некоторому числу.
15. Все значения, которые принимает независимая переменная Х образуют:
а) множество значений функции;
б) область определения функции;
в) способы задания функции.
16. Функция у = f(x) называется чётной на всей области определения, если для любого х Î D (у) справедливо условие:
а) f(– x) = f(x);
б) f(– x) = –f(x);
в) f(– x) ≠ f(x) и f(– x) ≠ –f(x).
17. Функцией называется монотонной на D(f), если…
а) … она только возрастает;
б) … большему значению аргумента соответствует большее значение функции;
в) … только возрастает или только убывает.
18. Если функция имеет набольшее значение, то…
а) … она ограничена сверху;
б) … она ограничена снизу;
в) … она не является ограниченной.
Тест №7 по теме «Преобразование графиков»
1. График функции у = x2 + 2 расположен:
а) в I и II координатных четвертях
б) в III и IV координатных четвертях
в) в I и IV координатных четвертях
г) в I и III координатных четвертях
2. График функции у = 1/x расположен:
а) в I и II координатных четвертях
б) в III и IV координатных четвертях
в) в I и IV координатных четвертях
г) в I и III координатных четвертях
3. График четной функции симметричен относительно:
а) оси Ох б) оси Оу в) начала координат г) прямой у = х
4. График нечетной функции симметричен относительно:
а) оси Ох б) оси Оу в) начала координат г) прямой у = х
5. Графики взаимно обратных функций симметричны относительно:
а) оси Ох б) оси Оу в) начала координат г) прямой у = х
6. Если для всех х из области определения функции f(x) выполняется равенство f(x-T) = f(x) = f(x+T), то функция f(x) является:
а) периодической б) четной в) нечетной г) ограниченной
7. Если для всех х из области определения функции f(x) выполняется равенство f(-х) = f(x), то функция f(x) является:
а) периодической б) четной в) нечетной г) ограниченной
8. Если для всех х из области определения функции f(x) выполняется равенство f(-х) = - f(x), то функция f(x) является:
а) периодической б) четной в) нечетной г) ограниченной
9. Если для всех х1 и х2 из области определения функции f(x), таких, что х1 > х2, выполняется равенство f(x1)> f(x2), то функция f(x) является:
а) возрастающей б) убывающей в) ограниченной сверху г) ограниченной снизу
10. Если для всех х1 и х2 из области определения функции f(x) , таких, что х1 > х2, выполняется равенство f(x1)< f(x2), то функция f(x) является:
а) возрастающей б) убывающей в) ограниченной сверху г) ограниченной снизу
11. Если для всех х из области определения функции f(x) выполняется равенство f(x)≥С, то функция f(x) является:
а) возрастающей б) убывающей в) ограниченной сверху г) ограниченной снизу
12. Если для всех х из области определения функции f(x) выполняется равенство f(x)≤С, то функция f(x) является:
а) возрастающей б) убывающей в) ограниченной сверху г) ограниченной снизу
13. Прямая, к которой график функции стремится приблизиться в бесконечности, но не пересекает ее, называется:
а) асимптотой б) касательной в) аппликатой г) осью координат
14. Прямая, которая имеет с графиком функции только одну общую точку на некотором промежутке, предельное положение секущей – это:
а) асимптота б) касательная в) аппликата г) ось координат
15. График функции y = f(x-a) получается из графика функции f(x) сдвигом:
а) вправо на а б) влево на а в) вверх на а г) вниз на а
16. График функции y = f(x) + b получается из графика функции f(x) сдвигом:
а) вправо на b б) влево на b в) вверх на b г) вниз на b
17. График функции y = - f(x) получается из графика функции f(x) преобразованием симметрии относительно:
а) оси Ох б) оси Оу в) начала координат г) прямой у = х
18. График функции y = f(-x) получается из графика функции f(x) преобразованием симметрии относительно:
а) оси Ох б) оси Оу в) начала координат г) прямой у = х
19. График функции y = k f(x) (k>1) получается из графика функции f(x):
а) сжатием в k раз по оси Ох
б) растяжением в k раз по оси Ох
в) сжатием в k раз по оси Оу
г) растяжением в k раз по оси Оу
20. График функции y = f(kx) (k>1) получается из графика функции f(x):
а) сжатием в k раз по оси Ох
б) растяжением в k раз по оси Ох
в) сжатием в k раз по оси Оу
г) растяжением в k раз по оси Оу
Тест №8 по теме «Многогранники»
Вариант 1.
1. Не существует призмы, у которой все грани …
1) ромбы; 2) прямоугольники; 3) треугольники.
2. 6 – это число …
1) вершин шестиугольной призмы;
2) рёбер треугольной призмы;
3) граней четырёхугольной призмы.
3. Какое утверждение неверное?
1) Боковые рёбра правильной призмы перпендикулярны плоскостям оснований.
2) Если боковые рёбра призмы перпендикулярны плоскостям оснований, то она правильная.
3) В основании правильной призмы лежит правильный n- угольник.
4. Существует призма, которая имеет …
1) 13 рёбер; 2) 14 рёбер; 3) 15 рёбер.
5. Какое утверждение верное?
1) Все рёбра правильной пирамиды равны.
2) Площадь поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
3) Боковые грани усечённой пирамиды – трапеции.
6. Боковые рёбра пирамиды SABC равны между собой. SD – высота пирамиды. Точка D лежит внутри ∆ ABC. ∆ ABC …
1) прямоугольный; 2) остроугольный; 3) тупоугольный.
7. Не является правильным многогранником …
1) правильная призма; 2) правильный тетраэдр; 3) правильный октаэдр.
8. Гранью правильного многогранника не может быть правильный …
1) треугольник; 2) пятиугольник; 3) шестиугольник.
9. Найдите число диагоналей прямоугольного параллелепипеда.
1) 2. 2) 4. 3) 6. 4) 8.
10. Найдите число диагоналей 6-угольной призмы.
1) 6. 2) 12 . 3) 9. 4) 18.
11. Какой многоугольник лежит в основании пирамиды, имеющей 12 ребер?
1) Треугольник. 2) Четырехугольник.
3) Шестиугольник. 4) Двенадцатиугольник.
12. Какой многоугольник лежит в основании призмы, имеющей 36 ребер?
1) Шестиугольник. 2) Девятиугольник.
3) Двенадцатиугольник. 4) Тридцатишестиугольник.
13. Призма имеет 18 вершин. Какой многоугольник лежит в ее основании?
1) Треугольник. 2) Шестиугольник.
3) Девятиугольник. 4) Восемнадцатиугольник.
14. Пирамида имеет 10 вершин. Какой многоугольник лежит в ее основании?
1) Пятиугольник. 2) Шестиугольник.
3) Восьмиугольник. 4) Девятиугольник.
15. Призма имеет 18 диагоналей. Определите ее вид.
1) Треугольная. 2) Шестиугольная.
3) Девятиугольная. 4) Восемнадцатиугольная.
16. Сколько диагоналей имеет 7-угольная пирамида?
1) Ни одной. 2) 6. 3) 7. 4) 14.
17. Какое утверждение неверное?
1) В основании правильной призмы лежит правильный п – угольник.
2) Если в основании призмы лежит правильный п – угольник, то она правильная.
3) Боковые рёбра правильной призмы перпендикулярны плоскостям оснований.
18. 9 – это число …
1) вершин девятиугольной призмы;
2) рёбер треугольной призмы;
3) граней четырёхугольной призмы.
19. Не существует призмы, у которой все грани …
1) ромбы; 2) квадраты; 3) трапеции.
20. Число рёбер призмы кратно …
1) 5; 2) 2; 3) 3.
21. По формуле Sбок = Pосн · Н нельзя вычислить площадь боковой поверхности …
1) прямой призмы; 2) правильной призмы; 3) наклонной призмы.
22. Какое утверждение верное?
1) Все грани правильной пирамиды равны.
2) Площадь боковой поверхности правильной усечённой пирамиды равна произведению суммы периметров оснований на апофему.
3) Боковые грани усечённой пирамиды – трапеции.
23. Боковые рёбра пирамиды SABC равны между собой. SD – высота пирамиды. Точка D – середина ребра BC. ∆ ABC …
1) прямоугольный; 2) остроугольный; 3) тупоугольный.
24. Не является правильным многогранником …
1) правильный тетраэдр; 2) правильная пирамида; 3) гексаэдр.
Тест №9 по теме «Многогранники и круглые тела»
1. Сколько касательных можно провести через данную точку шаровой поверхности?
А) одну; Б) бесконечно много; В) ни одной.
2. Осевое сечение усечённого конуса является …
А) равнобедренным треугольником; Б) прямоугольником; В) равнобокой трапецией.
3. Как называется плоскость, проходящая через образующую цилиндра, перпендикулярно осевому сечению?
А) секущая; Б) касательная; В) образующая.
4. Осевое сечение цилиндра является …
А) равнобедренным треугольником; Б) равнобокой трапецией. В) прямоугольником
5. Как называется плоскость, проходящая через образующую конуса и центр основания?
А) секущая; Б) осевое сечение; В) образующая.
6. Что представляет собой сечение конуса плоскостью, проходящей через его вершину и параллельное его основанию?
А) Точка; Б) Отрезок; В) Круг; Г) Равнобедренный треугольник.
7. Пирамида – это . . .
А) Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и параллелограммов;
Б) Многогранник, составленный из n-угольника и треугольников;
В) Правильный многогранник, составленный из двадцати равносторонних треугольников.
8. Какая фигура получится в осевом сечении конуса, у которого радиус основания конуса равен половине образующей?
А) Равносторонний треугольник; Б) Равнобедренный треугольник;
В) Окружность; Г) Прямоугольник.
9. Поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки называется
А) Цилиндр Б) Сфера В) Параллелепипед Г) Конус
10. Какая фигура получится в осевом сечении цилиндра?
А) Круг; Б) Треугольник; В) Прямоугольник; Г) Пятиугольник.
11. Какая из перечисленных фигур не является сечением конуса
А) Точка; Б) Круг; В) Трапеция; Г) Треугольник.
12. Боковой гранью правильной пятиугольной усечённой пирамиды является . . .
А) Треугольник; Б) Равнобедренный треугольник;
В) Равнобедренная трапеция; Г) Прямоугольник.
13. Сколько граней имеет правильная треугольная призма?
А) 6; Б) 8; В) 12; Г) 9.
14. Какая фигура получиться в сечении конуса, параллельно плоскости основания?
А) Круг, радиус которого больше радиуса основания конуса;
Б) Круг, радиус которого меньше радиуса основания конуса;
В) Круг, радиус которого равен радиусу основания конуса;
Г) Равнобедренный треугольник.
15. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть . . .
А) Плоскостью; Б) Двугранным углом; В) Гранью многогранника; Г) Многогранником.
16. Какое наименьшее число ребер может иметь многогранник?
А) 6 Б) 3 В) 8 Г) 9
17. Конус нельзя получить путем вращения . . .
А) Прямоугольника вокруг боковой стороны;
Б) Равнобедренного треугольника вокруг его оси;
В) Прямоугольного треугольника вокруг катета;
Г) Равностороннего треугольника вокруг оси его.
18. Боковой гранью правильной треугольной усечённой пирамиды является . . .
А) Треугольник;
Б) Равнобедренный треугольник;
В) Равнобедренная трапеция;
Г) Прямоугольник.
19. Какое из перечисленных фигур не является сечением цилиндра
А) Круг; Б) Прямоугольник; В) Треугольник; Г) Ромб.
20. Какая фигура получится в сечении конуса, которое параллельно плоскости основания?
А) Круг, радиус которого меньше радиуса основания конуса;
Б) Круг, радиус которого больше радиуса основания конуса;
В) Круг, радиус которого равен радиусу основания конуса;
Г) Равнобедренный треугольник.
21. Тело, ограниченное конической поверхностью и кругом с границей L, называется . . .
А) Конусом; Б) Цилиндром; В Параллелепипедом; Г) Сферой.
22. Диагонали параллелепипеда . . .
А) Не пересекаются;
Б) Не пересекаются, но численно равны;
В) Пересекаются в одной точке и делятся в этой точке пополам;
Г) Пересекаются и перпендикулярны.
23. Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1, называется . . .
А) Конусом; Б) Цилиндром; В) Параллелепипедом; Г) Сферой.
24. Полная поверхность пирамиды – это . . .
А) Сумма площадей всех её граней ;
Б) Произведение основания на боковую поверхность;
В) Разность боковой поверхности и основания
25. Цилиндр можно получить путем вращения
А) Прямоугольника; Б) Треугольника; В) Трапеции; Г) Пятиугольника.
26. Какая фигура получится в осевом сечении конуса, у которого радиус основания конуса равен половине образующей?
А) Равносторонний треугольник; Б) Равнобедренный треугольник;
В) Окружность; Г) Прямоугольник.
27. Какая фигура получится в сечении цилиндра, если секущая плоскость параллельна плоскостям оснований?
А) Прямоугольник; Б) Треугольник; В) Круг; Г) Пятиугольник
28. Призма – это . . .
А) Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и параллелограммов;
Б) Правильный многогранник, составленный из двадцати равносторонних треугольников;
В) Многогранник, составленный из -угольника и треугольников.
29. Боковой гранью правильной шестиугольной усечённой пирамиды является . . .
А) Треугольник; Б) Равнобедренный треугольник;
В) Равнобедренная трапеция; Г) Прямоугольник.
Тест №10 по теме «Производная и ее приложения»
1. Предел отношения приращения функции в точке х к приращению аргумента, когда последнее стремится к нулю называется…
а) производной функции
б) неопределенным интегралом
в) пределом функции
г) первообразной
2. Если материальная точка движется по закону S(t), то первая производная от пути по времени есть…
а) угловой коэффициент
б) ускорение движения
в) скорость в данный момент времени
г) сила, действующая на точку.
3. Геометрический смысл производной состоит в том, что …
а) она равна пределу функции
б) она равна всегда нулю
в) она равна угловому коэффициенту касательной
г) она равна максимальному значению функции
4. Дифференцирование – это…
а) вычисление предела
б) вычисление приращения функции
в) нахождение производной от данной функции
г) составление уравнения нормали
5.
Эта формула выражает 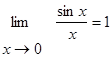
а) первый замечательный предел;
б) первообразную
в) угловой коэффициент касательной
г) максимальному значению функции
6. Уравнение касательной к данной линии в точке М имеет вид…
а) y-y0=y/(х)(х-х0) б) y= y/(х)(х-х0) в) y-y0=х-х0 г) y=y*х
7. Производная постоянной величины равна…
а) единице б) самой постоянной в) не существует г) нулю
8. При вычислении производной постоянный множитель можно…
а) возводить в квадрат
б) выносить за знак производной
в) не принимать во внимание
г) принять за нуль
9. Ускорение прямолинейного движения равно…
а) скорости от пути по времени
б) первой производной от пути по времени
в) второй производной от пути по времени
г) нулю
10. Функция возрастает на заданном промежутке, если…
а) первая производная положительна
б) вторая производная положительна
в) первая производная отрицательна
г) первая производная равна нулю
Тест №11 по теме «Интеграл и его применение»
1. Если F/(х)=f(х), то функция y = F(x) называется
а) производной для функции y = f(x)
б) дифференциал функции y = f(x)
в) первообразная для функции y = f(x)
г) касательной графику функции y = f(x)
2. Множество первообразных для данной функции f(х) называется…
а) функцией
б) неопределенным интегралом
в) дифференциалом
г) частной производной
3. Операция нахождения неопределенного интеграла называется…
а) дифференцированием функции
б) преобразованием функции
в) интегрированием функции
г) упрощением выражения
4. Непосредственное интегрирование, метод подстановки, интегрирование по частям это…
а) методы нахождения производной
б) методы интегрирования
в) методы решения задачи Коши
г) все ответы верны
5. Производная от неопределенного интеграла равна…
а) подынтегральной функции
б) постоянной интегрирования
в) переменной интегрирования
г) любой функции
6. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен…
а) произведению интегралов этих функций
б) разности этих функций
в) алгебраической сумме их интегралов
г) интегралу частного этих функций
7. Определенный интеграл вычисляют по формуле…
а) ![]()
![]() f(х)dx=F(a)-F(b);
б)
f(х)dx=F(a)-F(b);
б) ![]()
![]() f(х)dx=F(b)-F(a);
f(х)dx=F(b)-F(a);
в) ![]()
![]() f(х)dx=F(a)+F(b); г)
f(х)dx=F(a)+F(b); г) ![]()
![]() f(х)dx=F(a)
f(х)dx=F(a)
8. Определенный интеграл с одинаковыми пределами равен…
а) единице б) бесконечности в) нулю г) указанному пределу
9. При перемене местами верхнего и нижнего пределов интегрирования определенный интеграл…
а) остается прежним б) меняет знак в) увеличивается в два раза г) равен нулю
10. Определенный интеграл используется при вычислении…
а) площадей плоских фигур
б) объемов тел вращения
в) пройденного пути
г) всех перечисленных элементов
11. Если криволинейная трапеция,
ограниченная линией ![]() и прямыми y=0, x=a, x=b, вращается вокруг оси х, то объем
вращения вычисляется по формуле
и прямыми y=0, x=a, x=b, вращается вокруг оси х, то объем
вращения вычисляется по формуле
а) 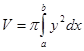 б)
б) 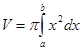 в)
в) 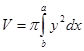 г)
г) 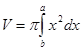
12. Если ![]() то площадь криволинейной трапеции,
ограниченной этой линией, двумя прямыми x=a и x=b и отрезком оси абсцисс a ≤ x ≤ b, вычисляется по формуле
то площадь криволинейной трапеции,
ограниченной этой линией, двумя прямыми x=a и x=b и отрезком оси абсцисс a ≤ x ≤ b, вычисляется по формуле
а) 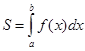 б)
б) 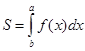 в)
в)  г)
г) 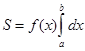
Тест №12 по теме «Элементы комбинаторики, событие и его вероятность»
1. Упорядоченное множество, отличающееся только порядком элементов, называется
а) перестановкой; б) размещением; в) сочетанием; г) разностью
2. Упорядоченное подмножество из n элементов по m элементов, отличающиеся друг от друга либо самими элементами либо порядком их расположения, называется …
а) сочетанием; б) размещением; в) перестановкой; г) разностью
3. … из n элементов по m называется любое подмножество из m элементов, которые отличаются друг от друга по крайней мере одним элементом.
а) перестановкой; б) размещением; в) сочетанием; г) разностью
4.Событие, которое обязательно произойдет, называется …
а) невозможным; б) достоверным; в) случайным; г) достоверным и случайным
5.Событие называется …, если оно не может произойти в результате данного испытания.
а) случайным; б) невозможным; в) достоверным; г) достоверным и случайным
6.Событие А и ![]() называется …, если
непоявление одного из них в результате данного испытания влечет появление
другого.
называется …, если
непоявление одного из них в результате данного испытания влечет появление
другого.
а) совместимым; б) несовместимым; в) противоположным; г) достоверными
7.Число перестановок определяется формулой
а) Pn=n! б)![]() в)
в) ![]() + n! г)
+ n! г) ![]()
8.Число сочетаний определяется формулой
а)
![]() б)
б) ![]() в)
в)![]() г)
г) ![]()
9.Вероятность достоверного события
а) больше 1; б) равна 1; в) равна 0; г) меньше 1
10.Вероятность невозможного события равна
а) больше 1; б) равна 1; в) равна 0; г) меньше 1
11.Отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний называется
а) классической вероятностью; б) относительной частотой;
в) физической частотой; г) геометрической вероятностью
12.Отношение меры области, благоприятствующей появлению события, к мере всей области называется
а) геометрической вероятностью; б) классической вероятностью;
в) относительной частотой; г) физической частотой
13.Вероятность появления события А определяется неравенством
а) 0<Р(А)<1 б) 0≤Р(А) ≤1 в) 0<Р(А) ≤1 г) 0<Р(А) ≤0,5
14.Сумма вероятностей противоположных событий равна
а) 1 б) 0 в) -1 г) 2
15.Вероятность РА(В) называется
а) классической вероятностью; б)геометрической вероятностью
в) условной вероятностью; г) относительной частотой
16.Формула ![]() называется
называется
а) формулой полной вероятности; б) формулой Бейеса;
в) формулой Бернулли г) формулой Ньютона
5. ПРОМЕЖУТОЧНЫЙ КОНТРОЛЬ ЗНАНИЙ
Вариант 1.
|
№ п/п |
Задание (вопрос) Инструкция по выполнению задания № 1 - 6 : соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв. Например,
|
||||
|
1. |
В каждое определение столбца 1 вставьте слово из столбца 2 (при необходимости изменив его падеж)
|
||||
|
2. |
Для каждой функции из столбца 1 укажите её график из столбца 2
|
||||
|
3. |
Для каждой функции из столбца 1 укажите её знаки в каждой координатной четверти из столбца 2
|
||||
|
4. |
В каждое определение столбца 1 вставьте слово из столбца 2
|
||||
|
5. |
Для каждой функции из столбца 1 укажите её график из столбца 2
|
||||
|
6. |
В каждое определение столбца 1 вставьте слово из столбца 2 (при необходимости изменив его падеж)
|
||||
|
|
Инструкция по выполнению заданий № 7 – 20: выберите букву, соответствующую правильному варианту ответа и запишите её в бланк ответов. |
||||
|
7. |
Формула
разложения квадратного трехчлена А.
В.
|
||||
|
8.
9.
|
Вычислить
значения выражения А. 3 Б. -1 В. 7 Г. 10
Найти
сумму корней уравнения А. -2 Б. 2 В. 1,5 Г. 0,5
|
||||
|
10. |
Решить неравенство 2х – 3 (х + 1) > 3 – 7 (2 - х) А. x<1 Б. x>1 В. x<-1 Г. x>-2
|
||||
|
11.
|
Найти
область определения функции А. В. |
||||
|
12. |
Найти площадь прямоугольника, если известно, что его периметр равен 18 см., а длина одной из сторон равна 5 см. А. 9 Б. 20 В. 36 Г. 400 |
||||
|
13. |
Решить
уравнение А. -5 Б. 1 В. -1 Г. 6
|
||||
|
14. |
Решить
уравнение А. 3 Б. -0,5 В. Корней нет Г. 0,5 |
||||
|
15. |
Вычислить
значение выражения А. -34 Б. 30 В. -30 Г. -28 |
||||
|
16.
|
А. 0 и 4 Б. 2 В. 3 Г. 2 и 3 |
||||
|
17. |
Упростить
выражение и вычислить его значение при
А.
0 Б. |
||||
|
18. |
Упростить выражение с помощью формул приведения
А. 0 Б. tg α В. – tg α Г. 0,5 |
Вариант 2.
|
№ п/п |
Задание (вопрос) Инструкция по выполнению задания № 1 - 6 : соотнесите содержание столбца 1 с содержанием столбца 2. Запишите в соответствующие строки бланка ответов букву из столбца 2, обозначающую правильный ответ на вопросы столбца 1. В результате выполнения Вы получите последовательность букв. Например,
|
||||
|
1. |
В каждое определение столбца 1 вставьте слово из столбца 2 (при необходимости изменив его падеж).
|
||||
|
2. |
Для каждой функции из столбца 1 укажите её график из столбца 2
|
||||
|
3. |
Для каждой функции из столбца 1 укажите её знаки в каждой координатной четверти из столбца 2.
|
||||
|
4. |
В каждое определение столбца 1 вставьте слово из столбца 2
|
||||
|
5. |
Для каждой функции из столбца 1 укажите её график из столбца 2.
|
||||
|
6.
|
Для каждой функции из столбца 1 укажите её производную из столбца 2.
|
||||
|
|
Инструкция по выполнению заданий № 7 – 20: выберите букву, соответствующую правильному варианту ответа и запишите её в бланк ответов. |
||||
|
7. |
Формула
корней квадратного уравнения А.
В.
|
||||
|
8.
|
Вычислить
значение выражения А. 3 Б. 9 В. 6 Г. 2 |
||||
|
9. |
Найти
произведение корней уравнения А.
-3 Б. В.
3 Г.
|
||||
|
10. |
Решить неравенство 20 – 4 (x - 1) < 5 - (2x - 3) А. x<8 Б. x>-4 В. x<-7 Г. x>8 |
||||
|
11. |
Найти
область определения функции А. В.
|
||||
|
12. |
Найти площадь прямоугольника, если его периметр равен 20, а длина равна 6. А. 24 Б. 32 В. 26 Г. 10 |
||||
|
13. |
Решить
уравнение А. -5 Б. 1 В. -1 Г. 6
|
||||
|
14.
|
Решить
равнение А. 3 Б. 24 В. 22 Г.-12 |
||||
|
15. |
Вычислить
значение выражения А. 7 Б. -2 В. 3 Г. -1 |
||||
|
16.
-5
|
Для функции, график которой изображён на рисунке, укажите экстремум.
А. -3 Б. -5 и 0,5 В. -6 Г. -3 и -6
|
||||
|
17. |
Упростить
выражение и вычислить его значение при
А.
0 Б. 3 В. -3 Г. |
||||
|
18. |
Упростить выражение с помощью формул приведения
А. 0 Б. – sin α В. 0,5 Г. sin α |
6. ОЦЕНОЧНЫЕ СРЕДСТВА для промежуточной аттестации
Теоретические вопросы к дифференцированному зачету
1. Приближённое значение величины. Погрешности приближений.
2. Комплексные числа. Алгебраическая форма записи и геометрическая интерпретация. Действия над комплексными числами.
3. Решение рациональных уравнений и неравенств. Метод интервалов.
4. Уравнения и неравенства с двумя переменными.
5. Определение степени с рациональным показателем. Свойства степеней.
6. Корни натуральной степени из числа и их свойства.
7. Определение логарифма. Свойства логарифмов.
8. Показательные уравнения и неравенства, способы их решения.
9. Логарифмические уравнения и неравенства, способы их решения.
10. Аксиомы планиметрии и стереометрии и следствия из них.
11. Взаимное расположение двух прямых в пространстве. Понятие скрещивающихся прямых.
12. Взаимное расположение прямой и плоскости в пространстве. Взаимное расположение двух плоскостей Параллельность плоскостей. Перпендикулярность плоскостей.
13. Проекция прямой на плоскость. Угол между прямой и плоскостью. Угол между плоскостями
14. Векторы на плоскости и в пространстве. Координаты вектора, длина вектора, равные, противоположные, коллинеарные и компланарные векторы.
15. Координаты вектора, длина вектора. Сложение векторов двумя способами, умножение вектора на число, скалярное произведение векторов. Вычисление угла между векторами.
16. Прямоугольная декартова система координат на плоскости и в пространстве. Координаты точки.
17. Уравнение прямой и окружности на плоскости.
18. Понятие числовой функции. Способы задания функции.
19. Область определения и область значений функции. Нахождение области определения функции для различного типа функций.
20. Основные свойства функции: чётность, нечётность, монотонность, ограниченность, периодичность.
21. Схема исследования функции. График функции.
22. Преобразования графиков: параллельный перенос, симметрия, растяжение вдоль осей координат.
23. Степенная функция, её свойства и графики.
24. Показательная функция y=ax (а>1) и (0<a<1).
25. Логарифмическая функция y=logx (a>1) и (0<a<1).
26. Понятие угла в тригонометрии. Меры измерения углов. Перевод из одной меры в другую.
27. Тригонометрические функции числового аргумента. Знаки тригонометрических функций в координатных четвертях.
28. Основные тригонометрические формулы. Формулы приведения.
29. Обратные тригонометрические функции.
30. Решение простейших тригонометрических уравнений.
31. Функция y=sinx, её свойства и график.
32. Функция y=cosx, её свойства и график.
33. Функция y=tgx, её свойства и график.
34. Функция y=сtgx, её свойства и график.
Практические задания
1. Найти абсолютную и относительную погрешности приближений.
2. Выполнить действия над комплексными числами.
3. Решить рациональное уравнение.
4. Решить рациональное неравенство.
5. Найти область определения функции.
6. Построить график функции и исследовать её.
7. Упростить выражение, содержащее степени и корни.
8. Упростить выражение, содержащее логарифмы, используя свойства логарифмов.
9. Решить показательное уравнение, неравенство.
10. Решить логарифмическое уравнение, неравенство
11. Упростить тригонометрическое выражение.
12. Найти значения тригонометрических функций по данному значению одной из них.
13. Решить тригонометрическое уравнение.
14. Найти длину вектора, угол между векторами.
15. Сложение векторов, скалярное произведение векторов, умножение вектора на число.
Теоретические вопросы к экзамену по математике
1. Приближённое значение величины. Погрешности приближений.
2. Комплексные числа. Алгебраическая форма записи и геометрическая интерпретация. Действия над комплексными числами.
3. Определение степени с рациональным показателем. Свойства степеней.
4. Корни натуральной степени из числа и их свойства.
5. Определение логарифма. Свойства логарифмов.
6. Основные понятия и аксиомы стереометрии и следствия из них.
7. Взаимное расположение двух прямых в пространстве. Понятие скрещивающихся прямых. Угол между прямыми.
8. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
9. Перпендикуляр и наклонная. Теорема о трех перпендикулярах.
10. Взаимное расположение плоскостей в пространстве. Угол между плоскостями.
11. Размещения из n элементов по m без повторений и с повторениями. Формула вычисления.
12. Перестановки из n элементов без повторений и с повторениями. Формула вычисления.
13. Сочетания из n элементов по m без повторений и с повторениями. Формула вычисления.
14. Прямоугольная система координат на плоскости и в пространстве. Координаты точки. Формулы расстояния между точками и координат середины отрезка.
15. Векторы на плоскости и в пространстве. Координаты вектора, длина вектора, равные, противоположные, коллинеарные и компланарные векторы.
16. Координаты вектора, длина вектора. Сложение векторов двумя способами, умножение вектора на число, скалярное произведение векторов. Вычисление угла между векторами.
17. Понятие угла в тригонометрии. Меры измерения углов. Формула перевода.
18. Тригонометрические функции числового аргумента. Знаки тригонометрических функций в координатных четвертях. Таблица значений тригонометрических функций основных углов.
19. Основные тригонометрические формулы. Формулы приведения.
20. Функция y=sinx, её свойства и график.
21. Функция y=cosx, её свойства и график.
22. Функция y=tgx, её свойства и график.
23. Функция y=сtgx, её свойства и график.
24. Построение графиков тригонометрических функций путем преобразования: параллельный перенос, симметрия, растяжение вдоль осей координат.
25. Обратные тригонометрические функции.
26. Решение простейших тригонометрических уравнений и неравенств.
27. Понятие числовой функции. Способы задания функции. График функции.
28. Область определения и область значений функции. Нахождение области определения функции для различного типа функций.
29. Основные свойства функции: чётность, нечётность, монотонность, ограниченность, периодичность.
30. Схема исследования функции.
31. Степенная функция, её свойства и графики.
32. Показательная функция y=ax (а>1) и (0<a<1).
33. Логарифмическая функция y=logx (a>1) и (0<a<1).
34. Призма. Прямая, наклонная, правильная призма. Формулы для вычисления площадей боковой и полной поверхности призмы. Объём призмы.
35. Параллелепипед. Прямой, прямоугольный, наклонный параллелепипед. Площади боковой и полной поверхности параллелепипеда. Объём параллелепипеда.
36. Пирамида. Прямая, наклонная, правильная пирамида. Формула для вычисления площади полной поверхности пирамиды. Объём пирамиды.
37. Усечённая пирамида. Формула для вычисления площади полной поверхности усечённой пирамиды. Объём усечённой пирамиды.
38. Круговой цилиндр. Прямой, наклонный цилиндр. Развёртка цилиндра. Площади полной и боковой поверхности цилиндра. Объём цилиндра.
39. Круговой конус. Прямой и наклонный конус. Развёртка конуса. Площади полной и боковой поверхности конуса. Объёма конуса.
40. Усечённый конус. Развёртка усечённого конуса. Площади полной и боковой поверхности усечённого конуса. Объём усечённого конуса.
41. Сфера и шар. Площадь поверхности сферы и объёма шара. Сечения сферы и шара плоскостями.
42.
Вычисление
пределов при х→a. Неопределённость вида [ ![]() ] (два случая). Привести один пример.
] (два случая). Привести один пример.
43.
Вычисление
пределов при х→∞. Неопределённость вида [ ![]() ] . Привести пример.
] . Привести пример.
44. Понятие производной функции. Правила и формулы нахождения производных. Производная сложной функции.
45. Исследование функций с помощью первой производной (критические точки, монотонность, экстремумы).
46. Исследование функций с помощью второй производной (выпуклость, вогнутость графика функции, точки перегиба).
47. Схема полного исследования функции.
48. Уравнение касательной и нормали. Геометрический смысл производной.
49. Применение производной в физике. Механический смысл производной.
50. Понятие первообразной функции и неопределённого интеграла. Правила и формулы нахождения неопределённых интегралов.
51. Определённый интеграл. Вычисление определённого интеграла с помощью формулы Ньютона- Лейбница.
52. Понятие криволинейной трапеции. Вычисление площади криволинейной трапеции с помощью формулы Ньютона- Лейбница.
53. Испытание, опыт. Событие, виды событий. Вероятность события. Классическое определение вероятности.
54. Дискретные и непрерывные случайные величины. Закон распределения дискретной случайной величины.
55. Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия и среднее квадратичное отклонение и их свойства.
56. Уравнения и неравенства с двумя переменными и их системы.
Практические задания
1. Упростить выражение, содержащее степени и корни.
2. Упростить выражение, содержащее логарифмы.
3. Решить показательное уравнение.
4. Решить логарифмическое уравнение.
5. Решить иррациональное уравнение.
6. Упростить тригонометрическое выражение.
7. Решить тригонометрическое уравнение.
8. Найти область определения функции.
9. Вычислить S бок, S пол, V: призмы, параллелепипеда, пирамиды, усечённой пирамиды, цилиндра, конуса, усечённого конуса, сферы, шара.
10. Вычислить предел функции при х→a, х→∞.
11. Найти производную функции.
12. Составить уравнение касательной к графику функции в данной точке.
13. Исследовать функцию на монотонность, экстремумы.
14. Исследовать график функции на выпуклость, вогнутость, точки перегиба.
15. Вычислить определённый интеграл.
16. Вычислить площадь фигуры, ограниченной линиями.
Экзаменационные билеты
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 1
1. Схема полного исследования функции.
2. Координаты вектора, длина вектора. Сложение векторов, умножение вектора на число, скалярное произведение векторов. Вычисление угла между векторами.
3.
Вычислить значение выражения ![]()
4.
Найти значение
производной функции f (x) =![]() в точке x0 = 2.
в точке x0 = 2.
5. Прямоугольник со сторонами 4 см и 6 см вращается вокруг большей стороны. Найти объем, площадь полной поверхности и площадь осевого сечения тела вращения.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 2
1. Комплексные числа. Алгебраическая форма записи и геометрическая интерпретация. Действия над комплексными числами.
2. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
3.
Вычислить значение выражения 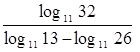
4.
Найти значение
производной функции f ( x) = ![]() в точке х0
= -2
в точке х0
= -2
5. Прямоугольник со сторонами 5 см и 8 см вращается вокруг меньшей стороны. Найти объем, площадь полной поверхности и площадь осевого сечения тела вращения.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 3
1. Степени и корни, их свойства.
2. Призма. Прямая, наклонная, правильная призма. Формулы для вычисления площадей боковой и полной поверхности призмы. Объём призмы.
3.
Найти значение
производной функции в точке х0 = -1 ![]()
4.
Вычислить значение выражения ![]()
5. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Найти объем, площадь полной поверхности, площадь осевого сечения и центральный угол развертки тела вращения.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 4
1. Тригонометрические функции числового аргумента. Меры измерения углов.
2. Взаимное расположение двух прямых в пространстве. Угол между прямыми.
3.
Решить
уравнение ![]()
4. Дана функция f(x) = х 3 – 3х 2-9х+2. Найти экстремумы функции.
5. Образующая конуса равна 13 см, а диаметр основания равен 24 см. Найти объём, площадь боковой поверхности и площадь осевого сечения конуса.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 5
1.
Вычисление
пределов при х→∞. Неопределённость вида [ ![]() ] . Привести пример.
] . Привести пример.
2. Параллелепипед. Прямой, прямоугольный, наклонный параллелепипед. Площади боковой и полной поверхности параллелепипеда. Объём параллелепипеда.
3.
Вычислить значение выражения ![]()
4. Дана функция f(x) = 3х 3 + 4,5х 2 - 1. Найти экстремумы функции.
5. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг большего катета. Найти объем, площадь полной поверхности, площадь осевого сечения и центральный угол развертки тела вращения.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 6
1. Определение логарифма. Свойства логарифмов.
2. Векторы на плоскости и в пространстве. Координаты вектора, длина вектора, равные, противоположные, коллинеарные и компланарные векторы.
3.
Решить
уравнение![]()
4.
Дана функция ![]() . Найти экстремумы функции.
. Найти экстремумы функции.
5. Образующая конуса равна 10см, а диаметр основания равен 16 см. Найти объём, площадь боковой поверхности и площадь осевого сечения конуса.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 7
1. Схема полного исследования функции.
2. Пирамида. Прямая, наклонная, правильная пирамида. Формула для вычисления площади полной поверхности пирамиды. Объём пирамиды.
3.
Решить
уравнение![]()
4. Дана функция f(x) = 2х 3 + 3х 2 – 4х + 2. Найти координаты точки перегиба графика этой функции.
5. Дан куб. Площадь полной его поверхности равна 150 см2. Найти объём куба и длину его диагонали.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8
1. Показательная функция y=ax (а>1).
2. Усечённая пирамида. Формула для вычисления площади полной поверхности усечённой пирамиды. Объём усечённой пирамиды.
3.
Решить
уравнение![]()
4. Дана функция f(x) = 3х 3 – 4,5х 2 – 5. Найти координаты точки перегиба графика этой функции.
5. В правильной треугольной призме сторона основания равна 2 см., боковое ребро – 4 см. Найти площадь боковой поверхности призмы и ее объем.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9
1. Тригонометрические функции числового аргумента. Меры измерения углов.
2. Круговой цилиндр. Прямой, наклонный цилиндр. Развёртка цилиндра. Площади полной и боковой поверхности цилиндра. Объём цилиндра.
3.
Решить
уравнение![]()
4.
Дана функция ![]() . Найти координаты точки перегиба
графика этой функции.
. Найти координаты точки перегиба
графика этой функции.
5. Дана треугольная призма, у которой все рёбра равны. Площадь боковой поверхности призмы равна 48 см². Найти периметр ее основания
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 10
1. Исследование функций с помощью второй производной (выпуклость, вогнутость графика функции, точки перегиба).
2. Круговой конус. Прямой и наклонный конус. Развёртка конуса. Площади полной и боковой поверхности конуса. Объёма конуса.
3.
Решить
уравнение![]()
4.
Вычислить
интеграл 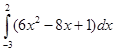
5. Дана правильная 4-угольная пирамида. высота пирамиды равна 12 см, диагональ основания равна 32 см. Найти боковое ребро и объём пирамиды.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 11
1. Функция y=sinx, её свойства и график.
2. Усечённый конус. Развёртка усечённого конуса. Площади полной и боковой поверхности усечённого конуса. Объём усечённого конуса.
3.
Решить
уравнение![]()
4.
Вычислить
интеграл ![]()
5. Дана треугольная призма, у которой все рёбра равны. Площадь боковой поверхности призмы равна 75 см². Найти периметр ее основания.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 12
1. Функция y=cosx, её свойства и график.
2. Сфера и шар. Площадь поверхности сферы и объёма шара. Сечения сферы и шара плоскостями.
3.
Решить
уравнение![]()
4.
Вычислить
интеграл 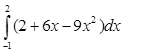
5. Дана правильная 4-угольная пирамида. высота пирамиды равна 15 см, диагональ основания равна 16 см. Найти боковое ребро и объём пирамиды.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 13
1. Понятие первообразной функции и неопределённого интеграла. Правила и формулы нахождения неопределённых интегралов.
2. Призма. Прямая, наклонная, правильная призма. Формулы для вычисления площадей боковой и полной поверхности призмы. Объём призмы.
3.
Решить
уравнение![]()
4. Вычислить площадь фигуры, ограниченной линиями y = 5-x2 ; y = 0 ; х = -1 ; х = 2.
5. Сколько шариков диаметром 2 см можно отлить из металлического кубика с ребром 4 см?
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 14
1. Уравнение касательной и нормали. Геометрический смысл производной. Механический смысл производной.
2. Взаимное расположение плоскостей в пространстве. Угол между плоскостями.
3.
Решить
уравнение![]()
4. Вычислить площадь фигуры, ограниченной линиями y =4х-х2 ;y = 0 ; х =3 .
5. Сколько кубиков с ребром 2 см можно отлить из металлического шарика диаметром 6 см?
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 15
1. Построение графиков функций путем преобразования графиков: параллельный перенос, симметрия, растяжение вдоль осей координат.
2. Перпендикуляр и наклонная. Теорема о трех перпендикулярах.
3. Вычислить
значение выражения ![]()
4.
Вычислить
площадь фигуры, ограниченной линиями ![]()
5. Площадь основания цилиндра равна 9 π (кв.см.), высота – 7 см. Найти площадь осевого сечения и площадь боковой поверхности цилиндра.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 16
1. Понятие криволинейной трапеции. Вычисление площади криволинейной трапеции с помощью формулы Ньютона- Лейбница.
2. Круговой цилиндр. Прямой, наклонный цилиндр. Развёртка цилиндра. Площади полной и боковой поверхности цилиндра. Объём цилиндра.
3.
Вычислить значение выражения![]()
4. Составить уравнение касательной, проведённой к графику функции f(x)=2x3-3x2+1 в точке с абсциссой х0= -2.
5. Площадь основания цилиндра равна 16 π (кв.см.), высота – 5 см. Найти площадь осевого сечения и площадь полной поверхности цилиндра.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 17
1. Понятие числовой функции. Способы задания функции. График функции.
2. Взаимное расположение двух прямых в пространстве. Угол между прямыми.
3.
Упростить
выражение 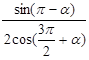
4. Составить уравнение касательной, проведённой к графику функции f(x)=-x3+2x2-3 в точке с абсциссой х0= -1.
5. Осевое сечение цилиндра – прямоугольник со сторонами 3 и 4 см., причём высота цилиндра равна 3 см. Найти объём цилиндра.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 18
1. Область определения и область значений функции. Нахождение области определения функции для различного типа функций.
2. Взаимное расположение прямой и плоскости в пространстве. Угол между прямой и плоскостью.
3.
Упростить
выражение ![]()
4.
Вычислить
предел ![]()
5. Дан цилиндр. Диаметр его основания равен 6 см. Высота больше радиуса в 3 раза. Найти объём цилиндра и площадь полной поверхности.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 19
1. Основные свойства функции: чётность, нечётность, монотонность, ограниченность, периодичность.
2. Перпендикуляр и наклонная. Теорема о трех перпендикулярах.
3.
Упростить
выражение ![]()
4.
Вычислить
предел ![]()
5. Дан цилиндр. Диаметр основания равен 6 см., высота цилиндра равна 4 см. Найти площадь боковой, полной поверхности цилиндра и его объём.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 20
1. Схема исследования функции.
2. Взаимное расположение плоскостей в пространстве. Угол между плоскостями.
3.
Известно, что ![]() . Найти
. Найти ![]()
4.
Вычислить
предел ![]()
5. Дан конус. Образующая конуса равна 13 см., высота – 12 см. Найти площадь полной поверхности конуса, его объём и угол развертки.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 21
1. Степенная функция, её свойства и графики.
2. Прямоугольная система координат на плоскости и в пространстве. Координаты точки. Формулы расстояния между точками и координат середины отрезка.
3.
Известно, что ![]() . Найти
. Найти ![]()
4.
Вычислить
предел ![]()
5. Образующая конуса равна 41 см., радиус основания – 9 см. Найти высоту конуса, его объём и угол развертки.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 22
1. Показательная функция y=ax (а>1).
2. Векторы в пространстве. Координаты вектора, длина вектора, равные, противоположные, коллинеарные и компланарные векторы.
3.
Упростить
выражение 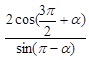
4.
Тело, массой 2
кг, движется прямолинейно по закону ![]() Найти
скорость и ускорение тела в момент времени 4 секунды.
Найти
скорость и ускорение тела в момент времени 4 секунды.
5. Дан конус. Длина окружности основания равна 8 π см., высота конуса равна 5 см. Найти объём конуса.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 23
1. Показательная функция y=ax (0<a<1).
2. Координаты вектора, длина вектора. Сложение векторов двумя способами, умножение вектора на число, скалярное произведение векторов. Вычисление угла между векторами.
3.
Вычислить
значение выражения ![]()
4.
Тело, массой 3
кг, движется прямолинейно по закону ![]() Найти
скорость и ускорение тела в момент времени 4 секунды.
Найти
скорость и ускорение тела в момент времени 4 секунды.
5. Прямоугольник со сторонами 4 см и 6 см вращается вокруг большей стороны. Найти объем, площадь полной поверхности и площадь осевого сечения тела вращения.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 24
1. Логарифмическая функция y=logаx (a>1).
2. Призма. Прямая, наклонная, правильная призма. Формулы для вычисления площадей боковой и полной поверхности призмы. Объём призмы.
3.
Вычислить
значение выражения ![]()
4.
Найти область
определения функции ![]()
5. Прямоугольник со сторонами 5 см и 8 см вращается вокруг меньшей стороны. Найти объем, площадь полной поверхности и площадь осевого сечения тела вращения.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 25
1. Логарифмическая функция y=logаx (0<a<1).
2. Параллелепипед. Прямой, прямоугольный, наклонный параллелепипед. Площади боковой и полной поверхности параллелепипеда. Объём параллелепипеда.
3.
Решить
уравнение и найти его корень при к = -2 ![]()
4.
Найти область
определения функции ![]()
5. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Найти объем, площадь полной поверхности, площадь осевого сечения и центральный угол развертки тела вращения.
ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 26
1.
Вычисление
пределов при х→a. Неопределённость вида [ ![]() ] (два случая). Привести пример.
] (два случая). Привести пример.
2. Пирамида. Прямая, наклонная, правильная пирамида. Формула для вычисления площади полной поверхности пирамиды. Объём пирамиды.
3.
Решить
уравнение и найти его корень при к = -1 ![]()
4.
Найти область
определения функции ![]()
5. Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг большего катета. Найти объем, площадь полной поверхности, площадь осевого сечения и центральный угол развертки тела вращения.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.