конспект М 6 ср скорость и комбинаторика

Конспект

Математика 6 класс

Решение задач на нахождение средней скорости

Чтобы найти среднюю скорость, надо:

1) найти весь пройденный путь;

2) найти все время движения;

3) весь пройденный путь разделить на все время движения:

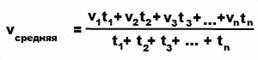
Пример1: Пешеход прошел 2 часа со скоростью 7 км/ч и 3 часа со скоростью 5 км/ч. Найти среднюю скорость движения пешехода на всем пути.

V₁=7 км/ч

t₁₌2ч

V₂=5 км/ч

t₂₌3ч

V_ср=?

Решение:

1)      Находим весь пройденный путь: V1· t1+ V₂· t₂=2∙7 + 3∙5 = 29 км.

2)      Находим все время движения: t1+ t₂=2+3=5 часов.

3)      Чтобы найти среднюю скорость, весь пройденный путь делим на все время движения: 29:5=5,8 км/ч.

Ответ: 5,8 км/ч.

Пример2: Велосипедист проехал 3 часа со скоростью 12 км/ч, затем отдохнул час, после чего продолжил путь со скоростью 9 км/ч и проехал еще 2 часа. Найти среднюю скорость движения велосипедиста на всем пути.

V₁=12 км/ч

t₁₌3ч

V₂=0 км/ч (отдыхал)

t₂₌1ч

V₃=9 км/ч

t₃₌2ч

V_ср=?

Решение:

Найдем весь путь велосипедиста: V1· t1+ V₂· t₂+ V₃· t₃

1)      3∙12 + 1∙0 + 2∙9 = 54 км.

Найдем все время движения: t1+ t₂+ t₃

2)      3 + 1 + 2 = 6 часов.

Чтобы найти среднюю скорость движения велосипедиста, весь путь делим на все время движения:

3)      54:6=9 км/ч.

Ответ: 9 км/ч.

Решение комбинаторных задач методом перебора

Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.

Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать».

Комбинаторные задачи – это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа.

Простые задачи решают обыкновенным  полным перебором  возможных вариантов без составления     различных таблиц и схем.

Например 1: Какие двузначные числа можно составить из цифр 1, 3, 4, 5?

Решение: 11,  13, 14, 15,  31, 33, 34, 35, 41, 43, 44, 45, 51, , 53,  54, 55.

Обозначим А – Антона, С – Сакена, Ю – Юру

1 день дежурит А                                  дежурит С                                        дежурит Ю

2 день дежурит С или Ю                      дежурит А или Ю                          дежурит А или С

3 день дежурит Ю или С                      дежурит Ю или А                          дежурит С или А

Решение этой задачи удобно изобразить графически, в виде дерева

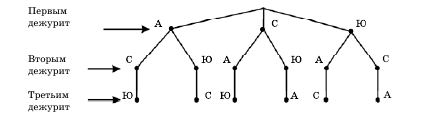
Теперь наглядно видно, что всего 6 вариантов дежурства: АСЮ, АЮС, САЮ, СЮА, ЮАС, ЮСА