Конспект урока: " Линейное уравнение с двумя переменными"

Дата:                                               

Предмет: Алгебра                                                                              

Класс: 8 а,б,в,г                                                        № 59

Тема: Линейное уравнение с двумя переменными, его график, примеры решения уравнений в целых числах

https://resh.edu.ru/subject/lesson/4728/start/158545/

Цели:

Образовательные: знакомство с определением линейного уравнения с двумя переменными; с определением решения уравнения с двумя переменными; со способом решения уравнений с двумя переменными; развитие навыка применения аналогии при решении задач;

закрепить знания учащихся о формулах сокращенного умножения.

Развивающие: способствовать развитию математического кругозора, мышления и речи, памяти учащихся.

Воспитательные: воспитывать у учащихся культуру общения, умение оценивать друг друга и давать себе самооценку.

Тип урока: Урок освоения новых знаний и умений.

На уроке предусмотрено использование следующих электронных образовательных материалов: «Диагностическая работа», «Самостоятельная работа».

Ключевые слова

Диофантовыми уравнениями называются уравнения вида

P(x₁, x₂, ..., x_n) = 0,

где P(x₁, ..., x_n) - многочлен с целыми коэффициентами.

Неопределенные уравнения – уравнения, содержащие более одного неизвестного. Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.

Теорема 1. Если НОД(а, b) = d, то существуют такие целые числа х и у, что имеет место равенство ах + bу = d.

Теорема 2. Если уравнение ах + bу = 1, если НОД(а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.

Теорема 3. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с не делится на d, то уравнение целых решений не имеет.

Теорема 4. Если в уравнении ах + bу = с НОД(а, b) = d>1 и с<d, то оно равносильно уравнению , в котором НОД  = 1.

Теорема 5. Если в уравнении ах + bу = с НОД(а, b) = 1, то все целые решения этого уравнения заключены в формулах:

х =  + bt, у = -at, где  - целое решение уравнения ах + bу = 1,

t – любое целое число.

Ход урока:

1.      Вхождение в тему урока и создание условий для осознанного восприятия нового материала:

1) «Страшная  опасность – это безделье за партой; безделье шесть часов ежедневно, безделье месяцы и годы. Это развращает».      В.А. Сухомлинский

Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач. Этими задачами много занимались самые выдающиеся математики древности, например, греческий математик Пифагор (VI век до н.э.), александрийский математик Диофант (III век н.э.), П.Ферма(XVII в.), Л.Эйлер(XVIII век), Ж.Л.Лагранж(XVIII век), П.Дирихле(XIX век), К.Гаусс(XIX век), П.Чебышев(XIX в.) и многие другие.

В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа быть не может, не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные  диофантовы уравнения. Поэтому мы должны для каждого уравнения выбирать собственный метод решения и более чем 10 методов, в основе которых лежат определения и свойства делимости чисел.

Проверка домашнего задания

1) 9x – 18y = 5

НОД (9;18)=9

5 не делится нацело на 9, в целых числах решений нет.

2) x + y= xy

Методом подбора можно найти решение

Ответ: (0;0), (2;2)

3) Составим уравнение:

Пусть мальчиков x, x Z, а девочек у, y Z, то можно составить уравнение 21x + 15y = 174

Многие учащиеся, составив уравнение, не смогут его решить.

Ответ: мальчиков 4, девочек 6.

2.      Освоение нового материала:

1)      Осуществление учебных действий по освоению нового материала

Столкнувшись с трудностями при выполнении домашнего задания, учащиеся убедились в необходимости изучения их методов решений неопределенных уравнений. Рассмотрим некоторые из них.

I. Метод рассмотрения остатков от деления.

Пример. Решить уравнение в целых числах 3x – 4y = 1.

3x = 4y + 1.

Левая часть уравнения делится на 3, следовательно, должна делиться и правая часть. Рассмотрим три случая.

1. Если y = 3m, m Z, то 4y + 1= 4•3m + 1 = 12m + 1 не делится на 3.
2. Если y = 3 m + 1, то 4y +1 = 4• (3m + 1)+1 = 12m + 5 не делится на 3.
3. Если y = 3 m + 2, то 4y +1 = 4• (3m + 2)+1 = 12m + 9 делится на 3, поэтому 3x = 12m + 9, следовательно, x = 4m + 3, а y = 3m + 2.

Ответ:  где m Z.

Описанный метод удобно применять в случае, если числа m и n не малы, но зато разлагаются на простые сомножители.

Пример: Решить уравнения в целых числах.

8x + 14y = 32

4x + 7y = 16

4x = 16 – 7y

Пусть y = 4n, тогда 16 - 7y = 16 – 7•4n = 16 – 28n = 4*(4-7n) делится на 4.

y = 4n+1, тогда 16 – 7y = 16 – 7• (4n + 1) = 16 – 28n – 7 = 9 – 28n не делится на 4.

y = 4n+2, тогда 16 – 7y = 16 – 7• (4n + 2) = 16 – 28n – 14 = 2 – 28n не делится на 4.

y = 4n+3, тогда 16 – 7y = 16 – 7• (4n + 3) = 16 – 28n – 21 = -5 – 28n не делится на 4.

Следовательно, y = 4n, тогда

4x = 16 – 7•4n = 16 – 28n, x = 4 – 7n

Ответ: , где n Z.

Галерея изображений (группа изображений по одной тематике)

3.      Применение изученного материала:

1)      Применение знаний, в том числе в новых ситуациях

Обсудите с учащимися предложенные примеры и задачи.

1) Решите в целых числах.

2) Найти целые неотрицательные решения уравнения:

Найти все пары целых чисел (x; y), удовлетворяющие следующим условиям

Решение:

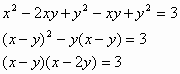
Число 3 можно разложить на множители:

3 = 1•3 = 3·1 = (-1)·(-3) = (-3)·(-1)

Ответ: (-1; -2), (5; 2), (1;2), (-5; -2).

4) Решить уравнения в целых числах

5) Решить уравнения в целых числах.

2)      Выполнение заданий в формате ГИА(ОГЭ,ЕГЭ)

Предложите учащимся решить задачу самостоятельно. Расскажите учащимся решение этой задачи.

4.      Подведение итогов, домашнее задание:

Рефлексия урока

1. Какое впечатление о нашем уроке?

2. Оцените свою деятельность на уроке?

3. Как вы себя чувствовали на уроке?

Оценки за урок.

Предложите учащимся задачи для самостоятельного решения дома.

Примеры. Решить уравнение в целых числах:

а) 

(x - y)(x + y)=4

Ответ: (-2;0), (2;0).

б) 

Ответы: (-10;9), (-5;3), (-2;-3), (-1;-9), (1;9), (2;3), (5;-3), (10;-9).

в) 

Ответ: (2;-3), (-1;-1), (-4;0), (2;2), (-1;3), (-4;5).