Возведение одночлена в степень
Цели: формировать умение возводить одночлен в степень и приводить его к стандартному виду.
Ход урока
I. Устная работа.
|
Разгадайте кроссворд. По вертикали: 2. Числовой множитель в одночлене стандартного вида. 3. Чему равен коэффициент одночлена a5bc5? 4. Чему равна степень одночлена 85? 5. Чему равна степень одночлена 102xy5z2? 6. Чему равно (–2)2? 7. Какое число получается при возведении отрицательного числа в нечётную степень? 8. Сумма показателей всех переменных одночлена. 9. Вид одночлена, в котором на первом месте числовой множитель, а за ним степени различных переменных. По горизонтали: 1. Выражение, которое содержит только числа, натуральные степени переменных и их произведения. |
|
Ответы: 1. одночлен. 2. Коэффициент. 3. Единица. 4. Ноль. 5. Восемь. 6. Четыре. 7. Отрицательное. 8. Степень. 9. Стандартный.
II. Объяснение нового материала.
1. Актуализация знаний.
Выполните устно умножение одночленов.
а) a3 ∙ a4; б)
a ∙ 
a2; в)
–a ∙ a2 ∙ a4;
г)
a ∙ (–x); д)
(–x) ∙ (–y); е)
(–x) ∙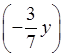 
;
ж)
(–2a) ∙ a2; з)
b2 ∙ (–3b3); и)
∙
6y;
к)
(0,2a) ∙ (–5b); л)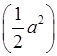 
∙
(–4ab); м) (–8m3) ∙ (–0,5n).
2. Теперь рассмотрим произведение двух или нескольких одинаковых одночленов, то есть степень одночлена. Например, (5a3b2c)2. Так как этот одночлен является произведением чисел 5, a3, b2, c, то по свойству возведения в степень произведения имеем:
(5a3b2c)2 = 52(a3)2(b2)2c2 = 25a6b4c2.
В результате возведения одночлена в натуральную степень снова получается одночлен.
III. Формирование умений и навыков.
1. № 472.
Решение:
а) 
;
б)
;
в)
;
г)
;
д)
;
е)
.
2. Выполните возведение одночлена в степень.
1) а) (6y)2; б)
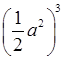; в)
(0,1c5)4;
2) а) (5ax)3; б) (4ac4)3; в) (5x5y3)3;
3)
а)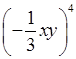 
; б)
(–10x2y6)3; в) (–a2b3c4)7;
4) а) –(3a2b)3; б) –(–2ab4)3; в) –(–a3b2c)4.
Решение:
1) а) 
;
б)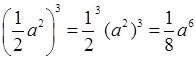 
;
в) 
.
2) а) 
;
б) 
;
в) 
.
3) а)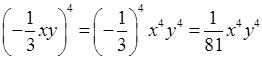 
;
б) 
;
в) 
.
4) а) 
;
б) 
;
в) 
.
При выполнении этих упражнений впоследствии можно не записывать подробно возведение в степень каждого сомножителя. Можно выполнять устно.
Следующие задания направлены на формирование умения раскладывать одночлен на множители либо представлять в виде степени некоторого одночлена.
3. № 475, № 477.
№ 475.
Решение:
а) 
;
б)
;
в)
;
г)
.
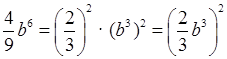№ 477.
Решение:
а) 
;
;
б)
;
.
4. № 479.
Решение:
а) 
;
.
б)
;
.
5. Упростите выражение.
1) а) 35a ∙ (2a)2; б) –4x3 ∙ (5x2)3; в) (–4y2)3 ∙ y5;
2)
а) 
; б)
.
Решение:
1) а) 
;
б) 
;
в) 
.
2) а)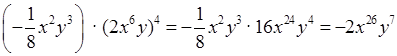 
;
б)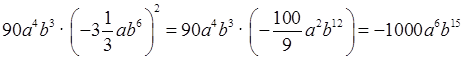 
.
IV. Проверочная работа.
Вариант 1
Выполните действия.
1) 
∙
(–24n) ∙ (4mn); 2) 
; 3)
(0,1a3b3)3.
Вариант 2
Выполните действия.
1) (–18n) ∙ 
∙
(–5mn); 2) 
; 3)
(0,4a3b2)2.
V. Итоги урока.
– Дайте определение одночлена.
– В каком случае мы говорим, что одночлен задан в стандартном виде?
– Сформулируйте определение степени одночлена. Приведите пример.
– Каким образом можно умножить одночлен на одночлен? Что получится в результате?
– Как возвести одночлен в степень? На какое правило мы при этом опираемся?
Домашнее задание: № 473; № 474; № 476; № 478; № 480.
Возведение одночлена в степень
Теперь рассмотрим произведение двух или нескольких одинаковых одночленов, то есть степень одночлена
При выполнении этих упражнений впоследствии можно не записывать подробно возведение в степень каждого сомножителя
IV. Проверочная работа. Вариант 1
© ООО «Знанио»
С вами с 2009 года.
