Конспект урока алгебры 8 класс по теме: "Решение двойных неравенств"

Решение двойных неравенств

устно выполнить данную работу

1. На с. 187 рассмотреть пример № 5.

Необходимо, чтобы учащиеся уяснили, что двойное неравенство представляют собой иную запись системы неравенств:

–1 < 3 + 2x < 3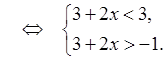

Решая систему, получим 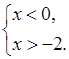 Полученное решение можно записать как в виде числового промежутка (–2; 0), так и в виде двойного неравенства –2 < x < 0.

2. Двойное неравенство можно решать и другим способом, используя теоремы-свойства числовых неравенств:

–1 < 3 + 2x < 3. Прибавляем к каждой части неравенства –3, получим:

–1 – 3 < 3 + 2x – 3 < 3 – 3,

–4 < 2x < 0. Разделим каждую часть неравенства на 2, получим:

–4 : 2 < 2x : 2 < 0 : 2,

–2 < x < 0.

Все упражнения, можно разбить на 4 группы:

1. Решение систем неравенств, содержащих дроби.

2. Решение двойных неравенств.

3. Решение систем трёх (и более) неравенств.

4. Решение заданий повышенной трудности.

I  г р у п п а. № 890 (а, в), № 891 (б, г).

Р е ш е н и е

№ 890.

а)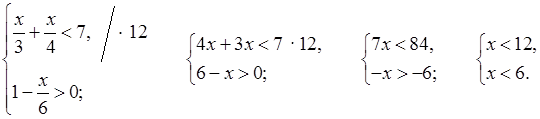

;            (–∞; 6).

в)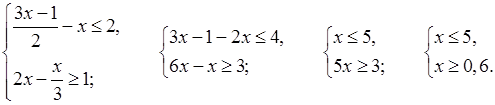

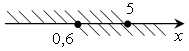;            [0,6; 5].

О т в е т: а) (–∞; 6); в) [0,6; 5].

№ 891.

б)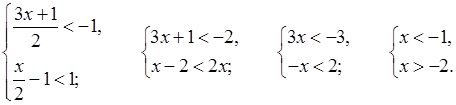

;            (–2; –1).

г)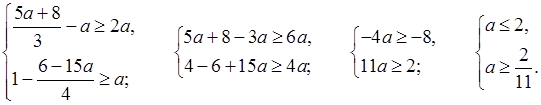

;            .

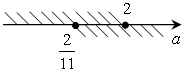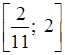О т в е т: б) (–2; –1); г) .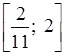

II  г р у п п а. № 893(б; г), № 894 (а; в), № 895 (а).

Р е ш е н и е

№ 893.

б) –1 <  ≤ 5;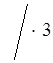

–3 < 4– а ≤ 15;

–3 – 4 < –а ≤ 15 – 4;

–7 < –а ≤ 11;

–11 ≤ а < 7;     [–11; 7).

г) –2,5 ≤  ≤ 1,5;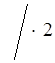

–5 ≤ 1 – 3у ≤ 3;

–5 – 1 ≤ –3у ≤ 3 – 1;

–6 ≤ –3у ≤ 2;

 ≤ у ≤ 2;     .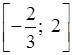

О т в е т: б) [–11; 7); г) .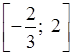

№ 894.

а) –1 ≤ 15a + 14 < 44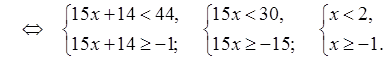

;            [–1; 2).

в) –1,2 < 1 – 2y < 2,4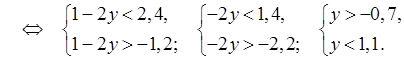

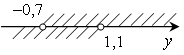;            (–0,7; 1,1).

О т в е т: а) [–1; 2); б) (–0,7; 1,1).

№ 895.

а) –1 < 3y – 5 < 1;

    4 < 3y < 6;

    1 < y < 2.

О т в е т: при 1 < y < 2.

III  г р у п п а. № 898 (а, в), № 899 (б).

Обращаем внимание, что в системе три неравенства, значит, решением является пересечение трёх числовых промежутков.

№ 898.

а) 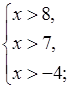 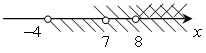       ;       (8; +∞).

в) 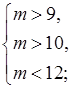 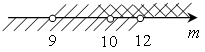       ;       (10; 12).

О т в е т: а) (8; +∞); в) (10; 12).

№ 899.

б)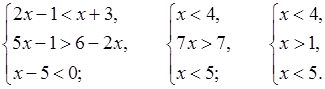

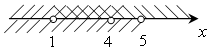;        (1; 4).

О т в е т: (1; 4).

IV  г р у п п а  (для сильных в учебе учащихся).

1. При каких значениях а система неравенств 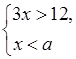 не имеет решений?

Р е ш е н и е

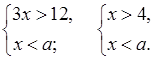  Чтобы система не имела решений, необходимо, чтобы (4; +∞) (–∞; а) = .

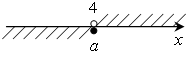          Это верно, если а ≤ 4.

О т в е т: при а ≤ 4.

2. № 896.

Р е ш е н и е

x² + 2xa + a² – 4 = 0 – квадратное уравнение.

D₁ = a² – (a² – 4) = 4, D₁ > 0, значит, уравнение имеет два различных корня. Найдём их:

x₁ = –a += –a + 2 = 2 – a;

x₂ = –a –= –a – 2.

Так как оба корня должны принадлежать интервалу (–6; 6), то одновременно выполняются условия:

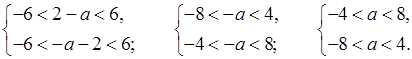
;        –4 < a < 4.

О т в е т: при –4 < a < 4.

Домашнее задание выполнить строго по образцу: повторить п. 32–35 (подготовка к контрольной работе); № 891 (а), № 895 (б), № 900 (а), № 889. (чтобы получить оценку 3 можно переписать решенные мной номера)