Конспект урока геометрии по теме "Теорема Пифагора"

Быстрякова Екатерина Сергеевна, МБОУ СОШ №5.

 

Название предмета	Геометрия
Класс	8
УМК	Геометрия, 7-9 классы: учебник для общеобразовательных организаций, авторы Л.С. Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – 6 изд.- М.: Просвещение, 2018.
Уровень обучения	Базовый
Тема урока	Теорема Пифагора
Общее количество часов, отведенное на изучение темы	1 час
Место урока в системе уроков по теме	10
Цель урока	Познакомить учащихся с некоторыми  фактами из биографии Пифагора, доказать теорему Пифагора, рассмотреть решение задач с её применением, показать учащимся тесную связь между алгеброй и геометрией, формировать познавательный интерес к предмету, совершенствовать приёмы устных вычислений
Задачи	1)Отрабатывать навыки применения теоремы Пифагора. 2) Активизировать память и внимание при решении письменных и устных задач. 3)Подвести учащихся к пониманию важности данной теоремы через различные аспекты ее применения.
Планируемые результаты	Знание формулировки теоремы Пифагора. Умение находить неизвестные стороны прямоугольного треугольника. Умение анализировать  условие задачи, с тем, чтобы применить теорему Пифагора. Осознавать важность теоремы и многогранность ее применения.
Техническое обеспечение урока	Компьютер, плазменная панель
Дополнительное методическое и дидактическое обеспечение урока	Портрет Пифагора, на стенде - карикатурные рисунки доказательства теоремы Пифагора, его «Золотые стихи»,  презентация.

  

Ход урока:

I.Организационный момент.

Этот урок будет посвящен знаменитой теореме геометрии-теореме Пифагора. Цель нашего занятия - познакомиться с биографией великого ученого древности, изучить одну из самых известных теорем, научиться использовать ее при решении задач. «Геометрия владеет двумя сокровищами, одно из них – теорема Пифагора».(слайд1)

 

II.Исторический экскурс.

(слайд2)

С берегов Средиземноморья – колыбели европейской цивилизации, с тех давних времен, названных «весною человечества», дошло до нас имя Пифагор. Это не только самый популярный ученый, но и самая загадочная личность, человек символ, философ, мистик,  религиозный и политический деятель, математик, пророк.

(слайд3)

Пифагор Самосский (570-490 гг.до н.э.) родился на острове Самос, расположенном в Эгейском море. Был учеником самого Фалеса  и по его совету в 22 года отправился набираться мудрости в Египет и более 20 лет обучался у египетских жрецов. Во время завоевательных походов на Египет он был захвачен в плен и продан в рабство в Вавилон. Там Пифагор более 10 лет изучал древнюю культуру и достижения науки разных стран.

(слайд4)

Вернувшись на родину, он организовал пифагорейский орден и школу философов и математиков. Туда принимали с большими церемониями и после долгих испытаний. В этой школе существовало правило, по которому авторство всех математических работ приписывалось самому Пифагору. В школе была очень серьезная дисциплина, запрещалось разглашать тайные знания. Сила личности Пифагора, его мудрость, высокая нравственность проповедуемых им идей и жизненных принципов притягивала к нему единомышленников. В его «братстве» насчитывалось около 2000 учеников и последователей.

(слайд5,6,7)

Кстати сказать, Пифагор – это не имя, а прозвище, которое философ получил за то , что всегда говорил верно и убедительно, это ещё одно из многих его качеств – великолепный оракул, которого слушали на площади до 800 человек.(Пифагор с др. греч.- «убеждающий речью».

Заслугой Пифагора и его школы были идеи о количественных закономерностях развития мира. В основе всего лежит число, учил Пифагор, познать мир - значит познать управляющие им числа. Пифагорейцы нашли числовые отношения во всех областях человеческой деятельности, что способствовало развитию математических, астрономических, физических и географических знаний. В этот период геометрия приобретает характер науки.

(слайд8)

Излюбленной геометрической фигурой пифагорейцев была пентаграмма или пифагорейская звезда. При встрече они рисовали ее на песке, приветствуя друг друга. Пентаграмма была паролем и символом, означая здоровье и счастье.

(слайд9)

Наконец, еще один штрих к портрету ученого. Он был, очень красив, 4 раза подряд становился олимпийским чемпионом, занимался музыкой, врачеванием, имел сына и дочь. Пифагор был убит в возрасте 90 лет во время народного восстания в уличной схватке.

(слайд10)

Достижения Пифагора и его школы:

-доказал теорему о сторонах прямоугольного треугольника

-ввел доказательство в геометрию

-заложил основы пропорций (геометрических, арифметических и гармонических)

-развил теорию музыки и акустики

-высказал предположение о шарообразности Земли

-всё в мире есть число-справедливость, смерть, постоянство, жизнь, любовь и прочее.

Пифагор сделал много важных открытий, но наибольшую славу ему принесла доказанная им теорема, которая носит его имя.

(слайд11)

III. Актуализация опорных знаний

Вот мы и подошли к изучению теоремы Пифагора, но сначала нам нужно проверить нашу готовность к изучению теоремы. (слайд12,13)

Ответьте мне на вопросы:

-Перечислите виды треугольников в зависимости от сторон

-Перечислите виды треугольников в зависимости от углов

-Какой треугольник называется прямоугольным?

-Как называются его стороны?

-Назовите катеты и гипотенузу в треугольнике, изображенном на рисунке

                                                                                                                                                                                                      

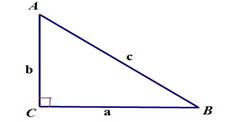
-Как найти площадь прямоугольного треугольника?

-Катеты прямоугольного треугольника равны 10 см и 16 см. Чему равна его площадь?

-Какой четырехугольник называется квадратом?

-Как найти его площадь?

-Сторона квадрата 9. Чему равна его площадь?

-Сторона квадрата равна  а+в. Чему равна его площадь?

Вы все молодцы, хорошо справились с заданиями! Можно переходить к доказательству теоремы.

IV. Изучение нового материала

(слайд14)

Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

 

Дано: прямоугольный треугольник с катетами а и в и гипотенузой с.

Доказать: с²=а²+в²

Доказательство:

(слайд15)

1. Достроим треугольник до квадрата со стороной (а+в).

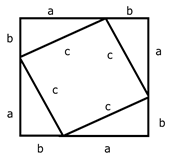
2. Разобьём квадрат на несколько фигур, получим 4 треугольника и квадрат, то, что это квадрат, мы с вами уже доказали при устной работе.

Вопросы для учащихся:

1.Какие получились треугольники?

2.Почему?

3. С одной стороны площадь квадрата равна сумме площадей четырёх равных треугольников и квадрата со стороной с.

S_кв = 4S_т+ S₁

S_кв =  + с² = 2ав + с²

4. С другой стороны площадь этого же квадрата равна сумме площадей двух прямоугольников со сторонами а и в и квадратов со сторонами а и в соответственно.

S_кв = 2ав + а² + в²

1.      Приравняем правые части этих выражений, получим:

2ав + с² = 2ав + а² + в²

Откуда имеем: с² =а² + в²    Теорема доказана.

(слайд16)

Шуточное стихотворение для запоминания теоремы:

Если дан нам треугольник,

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдем:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путем

К результату мы придем.

V. Исторический экскурс.

(слайд17)

Теорема Пифагора имеет огромное значение: она применяется в геометрии на каждом шагу. Существует более 300 различных доказательств этой теоремы ( геометрических, механических, с помощью шахматной доски, алгебраических и т.д.). В Вавилонских текстах это утверждение встречается за 1200 лет до Пифагора, но он первым нашёл ее доказательство. В честь своего открытия Пифагор принес в жертву быка, сделанного из пшеничного теста, так как по моральным и религиозным воззрениям  он «запрещал даже убивать животных, а тем более ими кормиться, ибо животные имеют душу, как и мы». Сам Пифагор не ел мяса, питался лишь мёдом, хлебом и фруктами.

VI . Устная работа по первичному закреплению знаний

(слайд18)

С помощью теоремы Пифагора можно решать два вида задач:

- Найти гипотенузу прямоугольного треугольника, если известны катеты

- Найти катет, если известны гипотенуза и другой катет

Задачи на готовых чертежах

(слайд19)

Вычислите устно:

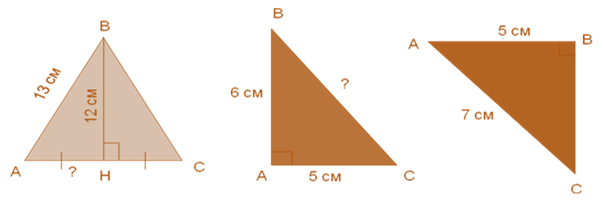
VII . Решение задач на закрепление знаний и отработку навыков

№483(б), №484(а) из учебника. Решаем письменно в тетрадях, учимся оформлять.

Задачи на применение теоремы Пифагора конечно же включены в ОГЭ, давайте решим некоторые из них.

Задачи из ОГЭ на применение т.Пифагора.

(слайд20)

Задача №1

Найти длину лестницы, один конец которой находится в 4 метрах от дома, а другой на стыке стены и крыши. Высота дома 8 метров.

Дано:                                                                                       К

 КDЕ,   D=90⁰                                                                          

DЕ=4 м,                                                                                  8

КD=8 м.

Найти: КD                                                                               D         4             Е

                                                                                                                        

Решение: КD²=DЕ² +DК²  (по т. Пифагора),  КD²= 16+64, КD²=80,  КD=4 м.

Замечаем, что сторона может быть выражена не рациональным числом.

Ответ: 4  м.

Задача 2.

В прямоугольной трапеции большая диагональ равна 25см, большее основание 24 см, меньшее основание 16 см. Найти площадь трапеции.

Дано:

АВСD-трапеция                                                                  A                     B

АС=25 см                                                                                      

ДС=24 см

АВ= 16 см                                                                            D                                    C

Найти:

S_ABCD

Решение:  S_тр.= ^AD
AD²=AC² –DC² ( по т. Пифагора), AD²= 25²-24², AD²=49, AD= 7,

 S_тр.==140 cм².

Ответ: 140 см².

Задача 3.

Диагонали ромба 6см и 8 см. Найти длину стороны ромба.                       B

Дано:                                                                                                                       

АBCD- ромб,                                                                                                                      

АС=6 см,                                                                                                A                           C

ВD=8 см.                                                                                                                           

Найти: АВ

Решить самостоятельно с последующей проверкой.                                      D

Ответ: 5 см.

 Задача 4.

Диагональ DB прямоугольника ABCD равна 61 см, а сторонa BC равна 11 см. Найти периметр прямоугольника.

Оформить и решить самостоятельно, соблюдая все требования оформления.

Ответ: 142 см.

VIII . Подведение итогов урока, выставление оценок.

(слайд21)

-Что нового вы сегодня узнали на уроке?

-Для каких треугольников применима теорема Пифагора?

-В чем заключается теорема Пифагора?

Выставление оценок учащимся.

IХ. Домашнее задание:

(слайд22)

Выучить формулировку и доказательство  т. Пифагора, п. 55

№483 (б), №484 (а)

Доп. задание – найти другие способы доказательства теоремы Пифагора.

(слайд23)

В конце урока еще одно «золотое правило» Пифагора: « Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться».

 

                                                       Спасибо за урок!