Конспект урока "Координатный метод: типовая задача о треугольнике""

Тема: Координаты вектора, скалярное произведение векторов.

Типовая задача о треугольнике.

Задания для самопроверки:

1. Написать разложение вектора  по координатным ортам.

2. Даны векторы  и  .

Найти векторы  ,  ,  .

3. Длины векторов  и  равны  и угол между векторами

 . Найти скалярное произведение векторов.

4. Найти длины векторов  и скалярное произведение этих векторов.

5. Найти угол между векторами  

Типовая задача с треугольником на плоскости, как правило, формулируется так: Даны три вершины треугольника. Требуется найти…

Пример 1

Даны вершины треугольника . Требуется:

1) составить уравнения сторон  и найти их угловые коэффициенты;
2) найти длину стороны ;
3) найти ;
4) составить уравнение высоты и найти её длину;
5) вычислить площадь треугольника ;
6) составить уравнение медианы ;
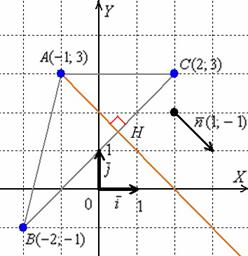
Решение: Начать целесообразно с выполнения чертежа. По условию этого можно не делать, но для самоконтроля и самопроверки всегда строим чертёж на черновике.

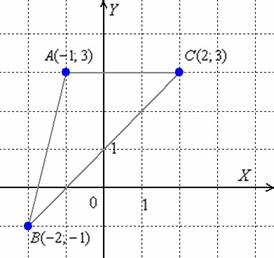
Ещё раз напоминаю, что самый выгодный масштаб 1 единица = 1 см (2 тетрадные клетки).

1) Составим уравнения сторон  и найдём их угловые коэффициенты.

Поскольку известны вершины треугольника, то уравнения каждой стороны составим по двум точкам.

Составим уравнение стороны  по точкам :

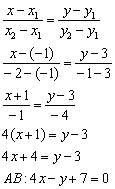
Для проверки следует мысленно либо на черновике подставить координаты каждой точки в полученное уравнение. Теперь найдём угловой коэффициент. Для этого перепишем общее уравнение в виде уравнения с угловым коэффициентом:

Таким образом, угловой коэффициент: 

Аналогично находим уравнения сторон . Не вижу особого смысла расписывать то же самое, поэтому сразу приведу готовый результат:

2) Найдём длину стороны . Для точек  используем формулу:

По этой же формуле легко найти и длины других сторон. Проверка очень быстро выполнятся обычной линейкой.

3) Найдём . Это угол при вершине . Есть несколько способов решения, но самый универсальный способ – находить угол при вершине, как угол между векторами.

Используем формулу .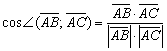

Найдём векторы:

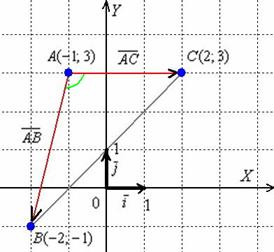
Таким образом:

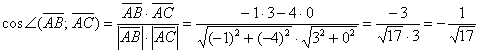
Кстати, попутно мы нашли длины сторон .

В результате:

 для убедительности к углу можно приложить транспортир.

4) Составим уравнение высоты и найдём её длину.

От строгих определений никуда не деться:

Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.

То есть, необходимо составить уравнение перпендикуляра, проведённого из вершины  к стороне .

Из уравнения  снимаем вектор нормали . Уравнение высоты  составим по точке  и направляющему вектору :

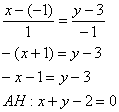
Обратите внимание, что координаты точки  нам не известны.

Точка известна: , уравнение прямой тоже известно: , Таким образом:

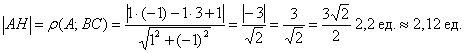
5) Вычислим площадь треугольника.

Используем школьную формулу:
 – площадь треугольника равна половине произведения его основания на высоту.

В данном случае:

6) Составим уравнение медианы .

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

а) Найдём точку  – середину стороны . Известны координаты концов отрезка: , тогда координаты середины:

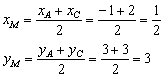
Таким образом: 

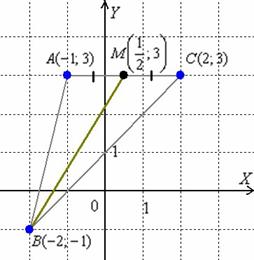
Уравнение медианы  составим по точкам :

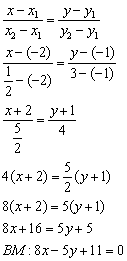
Чтобы проверить уравнение, в него нужно подставить координаты точек .

отношение 

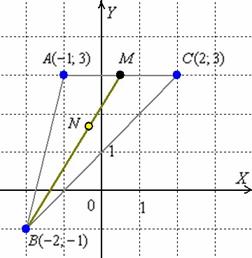
Нам известны точки .
По формулам деления отрезка в данном отношении:

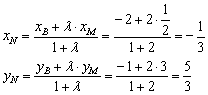
Таким образом, центр тяжести треугольника: 

Как уже отмечалось, на практике рассмотренная задача с треугольником на плоскости очень популярна.

Домашнее задание:

Решить задачу по образцу для треугольника с координатами  А(1;1) , В(6;5) и С(9;2)

Скачано с www.znanio.ru