MATRITSANING XOS SON VA XOS VEKTORLARNI TOPISH.

MATRITSANING XOS SON VA XOS VEKTORLARNI TOPISH.

Reja:

1.     Matritsani xos son va xos vektorini hisoblash.

2.     Xos qiymatlarni to’liq muammosini hal qilishda Krilov va Danilevskiy usullari.

3.     Xos qiymatlarning  qismiy muammolarini hal etishda turli usullar.

4.     Moduli bo’yicha eng katta xos son va xos vektorni berilgan aniqlikda topish.

Tayanch iboralar: Xos qiymat, xos vektor, minimal ko’phad, diagonal minor,  nol bo’lmagan vektor.

Agar biror noldan farqli  vektor uchun

tenglik bajarilsa, u holda  son A kvadrat matritsaning xos soni deyiladi. Bu tenglikni qanoatlantiradigan noldan farqli  vektor  matritsaning l xos soniga mos keladigan xos vektori deyiladi.

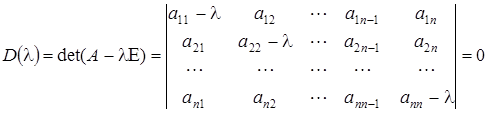            (1)

tenglama A  matritsaning xarakteristik tenglamasi deyiladi.

                              (2)

A matritsaning xos yoki xarakteristik ko’phadi deyiladi.

 Krilov usuli

Ixtiyoriy noldan farqli  vektor olamiz va   vektorlarni xosil qilamiz.

         Keli-Gamilton munosabatini yozamiz:

yoki

vektor tenglama hosil qilinadi. Buni ochib yozaylik

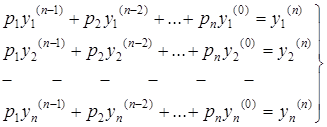                   (3)

(3) tenglamalar sistemasini misol uchun Gauss usuli bilan yechamiz va  larni topamiz, natijada (2) xos ko’phad qurilgan bo’ladi, so’ng

D(l) = 0

tenglamani yechib  l₁, l₂, ...,  lar topiladi.

         Endi xos vektorlarni topamiz.

 larni  vektorlar orqali yoyib olamiz

.

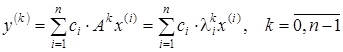quyidagi ko’phadni tuzamiz

 .

 vektorlarning quyidagi kombinatsiyasini tuzamiz

. (5)

Agar 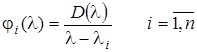   desak,  bo’lganligi uchun

bo’ladi.  koeffistientlar esa

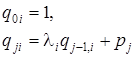
rekurrent formula yordamida topiladi.

         Agar (3) tenglamalar sistemasini yechishda Gauss usulini to’\ri yo’lini  ta qadami bajarilsa, u holda  vektorlar chiziqli erklidir. Shuning uchun (3) tenglamalar o’rniga quyidagi

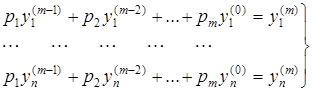
tenglamalar sistemasini yechib  lar topiladi va  tenglamadan  larni topamiz.

ko’phad  matritsaning minimal ko’phadi deyiladi.

Xos vektor esa quyidagicha topiladi

 ,

bu erda

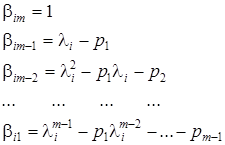
Misol 1.

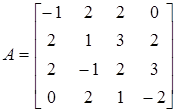
matritsaning xarakteristik ko’phadi topilsin.
Yechish.   deb olamiz. U xolda

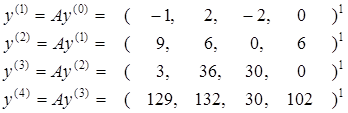
Endi (3) tenglamalarni yozamiz

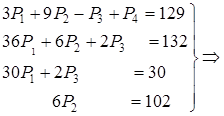
Misol 2.

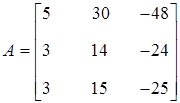
matritsaning xos son sonlari va xos vektorlari topilsin.

Yechish.     deb

larni hosil qilamiz va (3) sistemani yozamiz

.

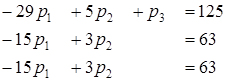Bu sistemani yechishda Gauss usulining uchinchi qadami bajarilmaydi, chunki 2 va 3-tenglamalar bir xil, demak   lar chiziqli bo\liq.

 larga bo\liq

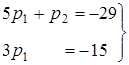
sistemani tuzamiz. Bundan    bo’ladi.

  deb   ni topamiz.  ni topish uchun, bizga ma’lum

 munosabatdan foydalanamiz

Endi xos vektorlarni topamiz:

,

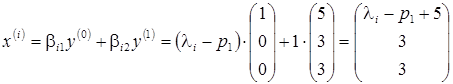
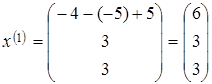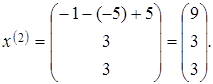
 ni topish uchun  vektorni boshqacha tanlash kerak.

Danilevskiy usuli

         Berilgan matritsa o’xshash almashtirish yordamida Frobenius

normal ko’rinishiga keltiriladi. Ma’lumki,  matritsaning xarakteristik ko’phadi  bo’ladi [1].

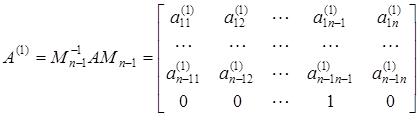
hosil qilinadi, so’ng  hosil bo’ladi.

         Har qadamdagi o’ngdan va chapdan ko’paytiriladigan matritsalarni ko’rinishini yozamiz

 ,

,

,

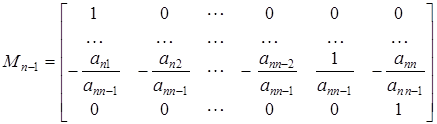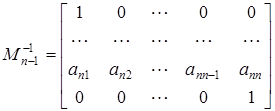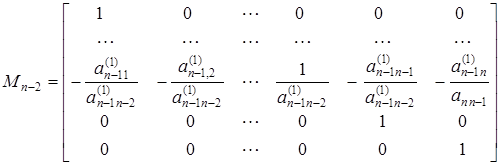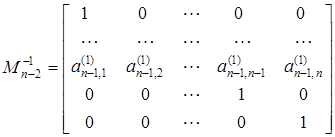
va hokazo. Natijada  matritsa Frobenius normal ko’rinishiga keladi.

  .

Danilevskiy usulida xos vektor   quyidagicha topiladi:

bu erda

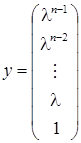
bo’lib, u    matritsaning xos vektoridir.   

Danilevskiy usulidagi noregulyar hol. Danilevskiy usulining  qadami bajarilgan bo’lsin va  ⁾ matritsa­ning  elementi nolga teng bo’lsin. Navbatdagi qadamni odatdagidek bajarib bo’lmaydi. Bunda agar  matritsaning  elementidan hamda, masalan, element  bo’lsa, ustunni ustun bilan almashtiramiz va xuddi shu nomerli satrlarni almashtirib yozamiz. Bunday almashtirishdan so’ng odatdagidek Danilevskiy usulini davom etdiramiz. Faraz qilaylik,

bo’lsin. U holda  quyidagicha ko’rinishga ega bo’ladi

.

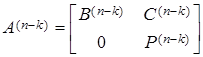         Bu erda  Frobenius normal formasiga ega bo’lgan  tartibli kvadrat matritsadir.  esa tartibli kvadrat matritsa bo’lib, uni odatdagidek Danilevskiy usuli bilan Frobenius normal ko’rinishga keltirish mumkin.

Xos sonlarni topishnng interpolyatsiya usuli.

Agar xarakteristik ko’pxad ma’lum bo’lsa uning ildizlarini topish qiyin emas. Masalan uni parabola yoki Nyuton usuli yordamida yechish mumkin. Lekin usullarni qo’llash paytida ko’pxadning qiymatini ko’p marotaba hisoblashga to’Іri keladi. Shu sababli ko’pіad qiymatini tez hisoblash usullarini qo’llash kerak. Eng sodda to’Іri usullardan biri interpolyatsiya usuli hisoblanadi. Xarakteristik ko’pxadni tuzish uchun ixtiyoriy  ta iymatlarni tanlab Nyutonning interpolyastion ko’pxadini ko’ramiz. Buning uchun qiymatlarni ya’ni xarakteristik ko’pxad qiymatlarini hisoblash kerak bo’ladi.

Bunda  xarakteristik ko’pxad arifmetik amal orqali aniqlanadi. Bu amallardan yarmi ko’paytirish amalini, yarmi qo’shish amalini tashkil qiladi. Agar ko’pxad tartibi  bo’lsa bu xarakteristik ko’pxadni EHM yordamida topish soniyaning bir nechta bo’lagida bajariladi. Agar xos sonlarning joylashish chegarasi ma’lum bo’lsa, unda ^(k) - larni shu oraliqda tekis joylashtirish maqsadga muvofiq. Chunki, Nyuton interpolyastion ko’pіadini qurish uchun ayirmali nisbatlarni hisoblashda bu usul turІun hisobni ta’minlaydi. Spektral radiusni topish uchun  tengsizlikdan foydalanish mumkin.

Ammo, A matritsa tartibi katta bo’lganda bu usul samarali bo’lmaydi.   

Birinchidan: xarakteristik ko’pіadni aniqlash uchun bajariladigan amallar soni n⁴  kabi oshadi.

Ikkinchidan: Nyuton ko’pіadini ko’rishda ayirmali nisbatlarni hisoblash aniqlikni yo’qotadi. Shuning uchun  bo’lganda (іamda xos sonlar karrali yoki bir-biriga yaqin bo’lganda) interpolyatsiya usuli yomon natija beradi.

Xarakteristik ko’pіad koeffistientlarini deyarli n3 ta amalda topib bera oladigan usullar mavjud. Masalan, A.N.Kro’lov, A.M.Danilevskiy, Samuelson,  Lanstosh kabi to’Іri usullar mavjud. Ammo bu usullar xam  bo’lgan іollarda turІun emaslar. Shuning uchun bu aniq usullarning tejamliligi interpolyatsiya usuliga qaraganda uncha katta emas.

 Uch diagonalli matritsalar xarakteristik ko’pіadini topish.

Interpolyastion usulda biz xarakteristik ko’pіadning yaqqol ko’rinishini, uning qiymatini biror-bir  da hisoblash uchun topgan edik. Ammo uch diagonalli matritsa uchun  determinantning qiymatini tez hisoblash usuli bor.

Bu shuning uchun іam muіimki, hatto yuqori tartibli matritsalarni іam o’xshash almashtirishlar yordamida uch diagonalli ko’rinishga keltirishning iloji bor.

Bu usul bilan tanishamiz.

 matritsaning m- tartibli bosh minorini  bilan belgilaymiz.

Bu minorni oxirgi satr elementlari bo’yicha yoyamiz, unda ikkita noldan farqli element bor. (1-shaklga qarang).

                                                  (13)

bu erda  orqali  elementni to’ldiruvchi minopi belgilangan. Bu minorni oxirgi ustun elementlari bo’yicha yoyamiz. Unda birta  element bor, shuning uchun

                                                                  (14)

buni yuqoridagi tenglikka qo’yib

                                  (15)

rekkurent tenglikni іosil qilamiz. Hisoblashni boshlashdan oldin, dastlabki ikkita minorni berish lozim.

Masalan:

                                                                 (16)

qilib olish mumkin.

Bulardan foydalanib  va  larni hisoblab, tanlovni  to’Іriligiga ishonch іosil kilish mumkin. Demak hisoblashni shunday boshlash qo’l keladi.

Determinant qiymatini bu rekkurent formula yordamida hisoblash uchun 5n-ta amal bajarish kerak, bundan tashqari amallar orasida bo’lish amali  yo’q bo’lib, hisoblash tez va turІundir. Shunday qilib xarakteristik ko’pіad qiymatini tez hisoblash usuli mavjud.  ko’pіad ildizlarini parabola usuli bilan topish mumkin. Bu usul tartibi uncha katta bo’lmagan  ko’pіadlar ildizlarini jumladan karrali ildizlarini, hisoblash uchun etarlicha turІun bo’lib, ildizlarni 5-7 ta ishonchli xonalarigacha topishga imkon beradi. EHMlarning programma ta’minotida (bibliotekasida) ko’pіadning barcha ildizlarini parabola usuli bilan hisoblash programmasi mavjud.

Teskari iteratsiya usuli.

Agar matritsaning xos soni ma’lum bo’lsa, unda

sistemani trivial bo’lmagan yechimlarini topish mumkin. Bu yechimlar matritsaning xos vektorlari bo’ladilar. Ammo, odatda taqribiy usullar xos sonlarni taqribiy topishga imkon beradilar. Shu sababli

lekin bu determinant nolga yakin. Shuning uchun

sistema faqat xq0 trivial yechimga ega bo’ladi.

Shu sababli sonli hisoblashda   sistemadan xos vektorni topib bo’lmaydi. Xos vektorlarni topish uchun qulay bo’lgan teskari iteratsiya usuli mavjud. Bu usul quyidagidan iborat. Ixtiyoriy ravishda b vektorni tanlaymiz va

                                                                                         (17)

sistemani qaraymiz.

Bu tenglama yagona yechimga ega. Bu sistemadan aniqlangan xos vektor l_i xos qiymatga deyarli yaqin bo’lishini ko’rsatamiz. Soddalik uchun n-tartibli A matritsa n ta   chiziqli boІliqmas xos vektorlarga ega bo’lgan іolni qaraymiz, masalan normal matritsa uchun. Bunda  vektorlar bazis tashkil qiladilar. Shuning uchun x va b - ni bu vektorlar orqali yoyamiz:

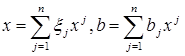                                                                             (18)

Bularni sistemaga quyib

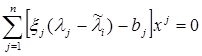
ega bulamiz.  xos vektorlar chiziqli boІliqmas bo’lganliklari uchun bu tenglik bo’lgandagina bajariladi.

Bundan

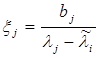                                                                                  (19)

Agar  bo’lsa  juda katta bo’ladi, aks іolda u katta emas. Bundan kelib chiqadigan natijalarning uch іolini qaraymiz.

Birinchi іol. -xos sonlar sodda bo’lgan іol. Unda barcha  koeffistientlaridan birtasi  eng katta bo’ladi. Bu topilgan x vektor  xos vektorga deyarli teng demakdir. Topilgan vektor juda katta bo’lganligi uchun uni odatda normallashtirishadi. Agar xos qiymatlar qo’pol topilgan bo’lsalar, yoki b vektor yomon tanlangan bo’lsa, b_i kichik bo’ladi. Bunda x_j bilan x orasidagi farq sezilarli bo’lishi mumkin. Bunda topilgan x vektorni (17) tenglamaga b o’rniga qo’yib iterastion jarayon tashkil qiladilar.

                                                                 (20)

Bu jarayon odatda juda tez yaqinlashadi va ikkita iteratsiya etarli bo’ladi.

1-IZOX. B vektorni tanlashning bir samarali usuli mavjud. Uning komponentalari sifatida g_k psevdo tasodifiy sonlarni oladilar. Bunda b_j ning juda kichik bo’lish  eіtimoli kam bo’ladi.

Ikkinchi іol.  karrali bo’lsin. Masalan,  Bunda  xos vektorlar ko’p qiymatli aniqlanadilar. Bularning ixtiyoriy chiziqli kombinastiyasi yana xos vektor bo’ladilar, ya’ni ular r o’lchovli fazo tashkil qiladilar va uning istalgan bazisini xos vektorlar sistemasi sifatida olish mumkin. Endi (19) –dan  koeffistientlarning katta bo’lishi, boshqa koeffistientlarning esa kichik bo’lishi kelib chiqadi. Bularning kuchayish koeffistientlari bir xil (17)-dan topilgan x vektor  vektorlarning chiziqli kombinastiyasidan iborat bo’ladi, shu bilan u qidirilayotgan vektor bo’ladi. Agar yaqinlashish aniqligi etarli bo’lmasa (20)- iteratsiyani davom ettirish lozim. Karrali xos qiymatlarning barcha xos vektorlarini topish uchun karrali soniga shuncha b^(k) chiziqli boІliqmas vektorni olish lozim. b^(k) komponentalarini psevdo tasodifiy sonlarni tanlash yo’li bilan aniqlash qulay. Bunda b^(k) vektorlar o’z-o’zidan chiziqli boІliqmas bo’ladilar.

Uchinchi іol. Xos qiymatlar karrali bo’lib, xos vektorlar soni n-dan kam. Bu іolda xam teskari iteratsiya usulini ishlatish mumkin. R  karrali xos qiymatga mos x^(k) vektorlar soni  bo’ladi. Bu x^(k) larni ortogonallashtirishda ma’lum bo’ladi. Birinchi -ta vektor іech qanday ortogonallashadilar, ammo undan keyingi vektorlarning komponentalari nolga juda yaqin bo’ladilar.

Teskari iteratsiyani birta xos vektorni topish uchun bir marta amalga  oshirilganda amal bajariladi, barcha xos vektorlarni topish uchun n₄ -ga yakin amal bajarish lozim. Shuning uchun bu usulni n<10 bo’lganda qo’llash yaxshi natija beradi. Bu usulning soddaligi va turІunligi uchun іam unda  foydalanish qulay. Xususiy іollarda  bu usulni qo’llash yana іam qulaydir. Xususan matritsa uch diogonalli bo’lganda (15)- sistemani progonka usuli bilan hisoblash kerak bo’ladi. Bunda іar bir xos vektorni topish uchun 10n- ta amal, barchasini topish uchun esa  arifmetik amallarni bajarish kerak.

Muіim bir narsani ta’kidlab o’tamiz.  bo’lganligi uchun progonka usuli bilan xos vektorlarni topish jarayonida bosh diogonalda eng kamida birta nolga yaqin element paydo bo’ladi. Hisoblashlarni olib borish uchun bosh diogonal elementlari noldan farqli bo’lishlari kerak, buning uchun xos sonlar xatoligi uncha kichik bo’lmasliklari kerak, ya’ni EHM ning 10-15  razryadlarini tashkil qilishlari kerak. Agar xos qiymatlar kesuvchilar yoki parabola usullari yordamida hisoblanayotgan bo’lsalar bunday xatolik paydo bo’ladi, chunki bu usullarda yaqinlashish sekin bo’ladi. Agar xos son Nyuton usuli yordamida topilayotgan bo’lsa xatolik nolga juda yaqin bo’lishi mumkin. Bunday іolda l_i larga sun’iy ravishda xatolik qo’yish kerak bo’ladi.

MISOL.. (3)-dagi S matritsasini va  taqribiy xos qiymatni olamiz. B vektor sifatida dekart koordinatalari birga teng vektorni olamiz. Unda (17)- tenglama

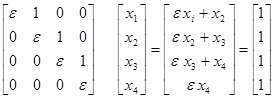
ko’rinishida yoziladi. x vektorning komponentalarini ketma-ket aniqlaymiz.

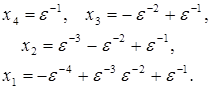
Undan so’ng normallashtiramiz. -ga ko’paytiramiz.

іosil qilingan  vektor Jordan matritsasining xos vektoriga taqribiy teng, shuni topish talab qilingan edi. Bu misol shuni ko’rsatadiki yuqori tartibli Jordan qismli matritsalarda EHMda xos vektorlarni hisoblash qiyin, chunki unda to’lib ketish sodir bo’ladi.

Moduli bo’yicha eng katta xos sonni va unga mos xos vektorni topish.

1-hol.      bo’lsin.

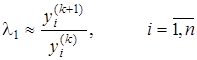, (1)

bu erda ,      

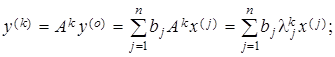
Agar (1) taqribiy tenglik barcha  uchun berilgan aniqlikda bajarilsa,  l₁  ning  qiymati topilgan bo’ladi.

         Xos vektorini    deb olish mumkin, chunki  dan sonli ko’paytuvchi bilan farq qiladi.

2-hol.   bo’lsin

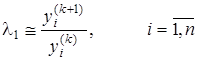
Xos vektor  1-holdagidek topiladi.

3-hol.

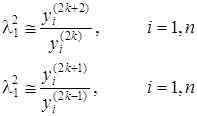
taqribiy tengliklardan  topiladi. 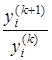 nisbat esa  da limitga ega bo’lmaydi. l₁ ga mos kelgan xos vektor sifatida  ni olamiz.  Agar  va  yoki bularning birortasi birdan katta bo’lsa, u holda boshqa dastlabki vektor tanlab jarayonni bajarish kerak.

Скачано с www.znanio.ru