Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 4. Интегральное исчисление и дифференциальные уравнения. Лекция № 8. Определённый интеграл.

Раздел 4. Интегральное исчисление и дифференциальные уравнения.

Лекция № 8. Определённый интеграл. (4 часа)

План лекции:

1. Определённый интеграл. (1 час)

2. Задача нахождения площади криволинейной трапеции.(1 час)

3. Формула Ньютона-Лейбница.(1 час)

4. Основные свойства определённого интеграла.(1 час)

Литература:

1. Электронный ресурс. О_3: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440, п. 11.1 – 11.16, стр.123.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

З₂.Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₃.Алгоритмы выполнения работ в профессиональной и смежных областях;

З₅.Структуру плана для решения задач.

Основные понятия:

Интегральной суммой для функции f(x) на отрезке [a, b] называется сумма, вычисляемая по формуле: S_n = f(ξ₁)Dx₁ +  f(ξ₂)Dx₂ + … + f(ξ_n )Dx_n =

Геометрически эта сумма изображается (представляется) ступенчатой фигурой, построенной из прямоугольников, и определяет площадь этой ступенчатой фигуры.

Определенным интегралом от f(x) на отрезке [a, b] называется предел интегральных сумм,  если при любых разбиениях отрезка [a, b] таких, что λ=maxDx_i® 0 и произвольном выборе точек ξ_i  для данного разбиения интегральная сумма  стремится к пределу I.

Обозначение определенного интеграла: I = 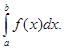, где а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок или промежуток интегрирования.

Если для функции f(x) существует предел интегральных сумм  и он конечный (число)

I=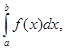то функция называется интегрируемой на отрезке [a, b].

Средним значением функции на отрезке [a, b] называется число µ: .

Если функция F(x) – какая- либо первообразная непрерывной функции f(x) на[a, b], то

 - это выражение известно под названием формулы Ньютона – Лейбница.

       Несобственные интегралы обобщают понятие определенного интеграла для 2-х случаев, при которых  нарушаются необходимые условия интегрируемости, а именно: 1)под интегралом  ограниченная функция f(x) интегрируется , по (полу-) бесконечному  промежутку и 2) под интегралом неограниченная функция g(x) интегрируется по конечному промежутку.

       Геометрически несобственные интегралы определяют площадь полубесконечной трапеции (рис), ограниченной в первом случае: графиком функции и осью ОХ; во втором случае графиком функции и осью OY по промежутку [d,0) (см. рис.).

      В задаче «найти несобственный интеграл …» решается проблема – какая по величине площадь криволинейной трапеции : конечная или бесконечно большая, что равносильно ответу на вопрос: сходится или расходится несобственный интеграл. .

Несобственным интегралом 1-го рода от функции f(x) на интервале [a, ¥) называется  предел  от интеграла с переменным верхним пределом,  когда последний (верхний предел) стремится к бесконечности .

Если предел существует и конечен, то говорят, что несобственный интеграл сходится.

Если предел не существует или бесконечен, то несобственный интеграл расходится.

Точки (c) на промежутке интегрировании в которых функции неограниченны называют особыми точками.  Особыми точками могут являться и  концы промежутка интегрирования. ,,

Несобственным интегралом второго рода  называется интеграл от неограниченной на отрезке функции по отрезку конечной длины.

Если функция  f(x) непрерывна при , неограниченна на правом конце отрезка, т.е.  и x=b особая точка, и существует интеграл по любому конечному промежутку [a,b-ε] где  ε- любое бесконечно малое число, то рассматривается предел от интеграла: 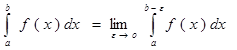и этот предел называется несобственным интегралом 2-го рода.

Несобственный интеграл второго рода 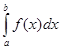 сходящийся, если предел существует и он конечный, если не существует или  бесконечно большой, то интеграл расходящийся.

1. Определённый интеграл.

       Понятие определенного интеграла и процедуры вычисления - интегрирования встречаются  в самых различных задачах физики, химии, техники, математической  биологии, теории вероятностей и математической статистики. К необходимости использовать определенный интеграл  приводят задачи вычисления площади криволинейной области, длины дуги, объема и  массы тела с переменной плотностью, пути пройденного движущимся телом, работы переменной силы, потенциала электрического поля и многое другое.

      Общим для этого типа задач является подход к решению задачи: большее можно представить как сумму маленького, площадь плоской области можно представить как сумму площадей прямоугольников, на которые мысленно разбивается область, объем как сумма объемов кусочков, масса тела как сумма масс частей и т.д.

      Математика обобщает прикладные задачи, заменяя физические, геометрические  величины абстрактными математическими понятиями  (функция, промежуток или область интегрирования), исследует условия интегрируемости и предлагает практические рекомендации к использованию определенного интеграла.

       Теория определенного интеграла является составной частью раздела математического анализа  - интегральное исчисление функции одной переменной.

Интегральная сумма.

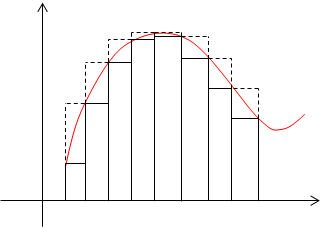
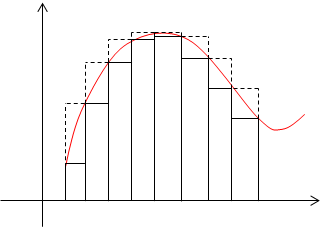
      В основе определения понятия определенный интеграл  лежит понятие интегральная сумма. Пусть на отрезке [a, b] задана непрерывная функция f(x). Будем называть криволинейной трапецией фигуру ограниченную графиком функции, осью ОХ и вертикальными прямыми, проходящими через концы отрезка (Рис.1). Обозначим площадь криволинейной трапеции S.

                                             y

                                           M

                                             m

                                              0       a=x₀                     x_i-1 ζ   x_i         x_n=  b                x

Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками.

a=x₀ < x₁ < x₂ < … x_i-1 < x_i …< b=x_n

Тогда длина каждой части (кусочка) Dx_i : x₁–x₀ = Dx₁, x₂–x₁= Dx₂, …, x_i–x_i-1=Dx_i  … ,

 x_n – x_n-1  = Dx_n.

Внутри каждого отрезка выберем некоторую точку ξ_i.

x₀ < ξ₁ < x₁,     x₁ < ξ₂ < x₂,  … x_i-1 < ξ_i  <  x_i ,…  , x_n-1 < ξ_n < x_n.

Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b].

S_n = f(ξ₁)Dx₁ +  f(ξ₂)Dx₂ + … + f(ξ_n )Dx_n =

Геометрически эта сумма изображается (представляется) ступенчатой фигурой, построенной из прямоугольников, и определяет площадь этой  ступенчатой фигуры.

В теории определенного интеграла большую роль играют суммы Дарбу. Они вводятся для выяснения  условий интегрируемости f(x) и существования определенного интеграла.

Определение: Определенным интегралом от f(x) на отрезке [a, b] называется предел интегральных сумм,  если при любых разбиениях отрезка [a, b] таких, что λ=maxDx_i® 0 и произвольном выборе точек ξ_i  для данного разбиения интегральная сумма  стремится к пределу I.

Обозначение определенного интеграла: I = 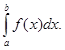, где а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок или промежуток интегрирования.

Определение: Если для функции f(x) существует предел интегральных сумм  и он конечный (число)

                                     I=

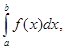
 то функция называется интегрируемой на отрезке [a, b].

Также верны утверждения: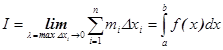

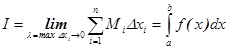
Теорема 1 (необходимое условие интегрируемости): Функция f(x) ограниченная  на [a, b] интегрируема.

Теорема 2 (достаточное условие интегрируемости): Если функция f(x) непрерывна  или кусочно-непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.

2. Задача нахождения площади криволинейной трапеции.

В данном пункте рассмотрим примеры прикладных задач геометрии и физики, в которых вычисление определенного интеграла  построенного по условиям задачи позволяет получить требуемый результат. В задачах этого раздела необходимо обратить внимание на обоснование получаемых рабочих формул.

Площадь плоских фигур в декартовой системе координат.

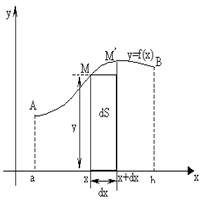Наиболее простая геометрическая задача: найти площадь фигуры, границы которой определены  уравнениями соответствующих линий и осью OX . В этом случае  рассматривается  криволинейная трапеция, о которой говорилось выше (рис. 1.) и используется  геометрический смысл определенного интеграла  как предел суммы площадей маленьких прямоугольников, образующих ступенчатую фигуру. Элементом площади в прямоугольной декартовой системе координат, полученным в процессе построения интегральной суммы, в этом случае служит прямоугольник площадь которого , Тогда площадь криволинейной трапеции находится по формуле:

S =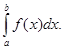, где S – площадь криволинейной трапеции, ограниченной графиком функции y=f(x), отрезком [a,b] на оси Ох и прямыми x=a и x=b,( a<b).

         Если функция принимает отрицательные значения  на промежутке интегрирования, или принимает значения разных знаков, то площадь находится как сумма модулей  значений интегралов вычисленных по промежуткам, на которых функция знакопостоянна – положительная или отрицательная.

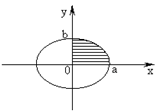
Пример 1. Найти площадь области ограниченной эллипсом .

Решение: Фигура (рис.2) симметрична относительно осей координат, поэтому достаточно найти , интегрируя по промежутку [0,a] функцию, график которой лежит в первой четверти и определяет верхнюю границу области . Запишем уравнение верхней границы области - эллипса для первого квадранта:   ,  xЄ [0,a], а интеграл вычисляем с помощью замены переменной

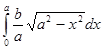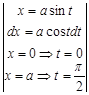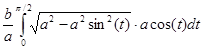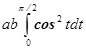=====     Ответ: Площадь эллипса

Если в задаче требуется – найти площадь области ограниченной графиками  функций, то промежуток интегрирования определяется    дополнительными     условиями, например, точками пересечения графиков. В этом случае формула для вычисления площади приобретает вид          (рис. 3).

,                  

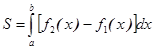где S – площадь криволинейной трапеции,

ограниченной графиками функций y=f₁(x) и y=f₂(x), f₂(x)³f₁(x), прямыми  x=a и x=b,( a<b).

Пример 2. Найти площадь фигуры ограниченной линиями  и .

На рис. 4 представлена фигура , ограниченная параболой и прямой, площадь которой требуется найти.

Найдем точки пересечения параболы и прямой для этого решим следующую систему уравнений:

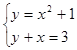Þ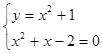

При решении квадратного уравнения системы

x²+x+2=0, получаем два корня х₁=-2, х₂=1 , которые являются координатами концов промежутка интегрирования для разности функций 

   f₁(x)= x²+1, f₂(x)=3-x (т.к. прямая лежит выше параболы в рассматриваемой области). В результате вычислений получаем : площадь области S=25/6. (Выполнить  вычисления самостоятельно)

Пример 3. Вычислить площадь фигуры, ограниченной линиями  и .

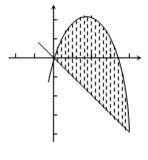
Решение. Находим точки пересечения данных кривых:

                                                 у

                                                             2

                                                                  х      

                                        −2  −1  O   1   2     3  4  

                                               −2

                                               −4

Рис.5

Следовательно, по формуле имеем (см. рис. 5)

.

3. Формула Ньютона-Лейбница.

Теорема: Для всякой функции f(x), непрерывной на отрезке [a, b], существует на этом отрезке первообразная, а значит, существует неопределенный интеграл.

Теорема: (Теорема-формула Ньютона – Лейбница):Если функция F(x) – какая- либо первообразная непрерывной функции f(x) на[a, b], то

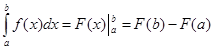
это выражение известно под названием формулы Ньютона – Лейбница.

Доказательство: Пусть F(x) – первообразная функции f(x). Тогда в соответствии с приведенной выше теоремой, функция 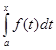 - первообразная функции f(x). Но т.к. функция f(x) может иметь бесконечно много первообразных, которые будут отличаться друг от друга только на какое – то произвольное постоянное число С, то

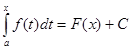
Это равенство справедливо для любого х на [a, b] , тогда при х=а получаем, после подстановки, следующие соотношения:

,   →  ,  →

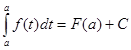Следовательно                                 .

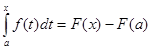Тогда  при х = b:                                

Заменив переменную t на переменную х, что не меняет смысла выражения, получаем формулу Ньютона – Лейбница (12):

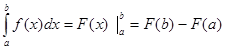
Теорема доказана.

Формула Ньютона – Лейбница определяет  основной подход к вычислению определенных интегралов – сначала надо найти первообразную подинтегральной функции, а затем подставить пределы и вычислить разность между значениями функции...

     Что касается приемов вычисления определенных интегралов, то они практически ничем не отличаются от всех тех приемов и методов, которые были рассмотрены при нахождении неопределенных интегралов (первообразной). Точно так же применяются знакомые методы: подстановки (замены переменной), метод интегрирования по частям, те же приемы нахождения первообразных для тригонометрических, иррациональных и трансцендентных функций. Особенностью является только то, что при применении этих приемов необходимо учитывать  преобразование не только подынтегральной функции, но и пределов интегрирования. Заменяя переменную интегрирования (вводя новую функцию), необходимо  не забыть изменить соответственно пределы интегрирования.

Пример. Вычислить определенный  интеграл .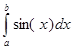

Решение: Так как для функции  f(x)=sin(x)  функция  F(x)=-cos(х)  является первообразной, то, применяя формулу Ньютона – Лейбница,  вычисляем данный определенный интеграл:    ===.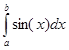

4. Основные свойства определённого интеграла

Свойства определенного интеграла.

1 .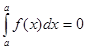

2. 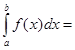--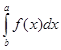 перестановка пределов интегрирования  приводит к изменению знака.

3.

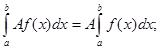
4.

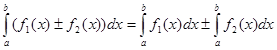
5. Если f(x) £ j(x) на отрезке [a, b]  a < b, то.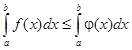

6. Оценки определенного интеграла : если m < M – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a, b], то:

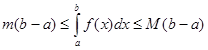
7. Теорема 3 (о среднем значении функции на отрезк). Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка x=c,  a<c<b, такая, что

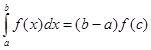
Доказательство:  В соответствии со свойством  6:

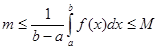, т.к. функция f(x) непрерывна на отрезке [a, b], то ( по свойству непрерывных на отрезке функций) она принимает на этом отрезке все значения от m до М. Другими словами, существует такое число cÎ [a, b], что если принять

m = f(c),  то 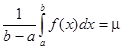      тогда 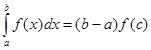. Теорема доказана.

Определение: Средним значением функции на отрезке [a, b] называется число µ :

.

Геометрическая интерпретация – формулы п.7 определяют  равенство площадей криволинейной трапеции и прямоугольника высотой  m = f(с) опирающихся на основание длиной   (b-a).

8. Для заданного промежутка интегрирования [a, b] и  и произвольной точки  c справедливо равенство:

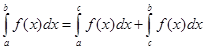
Разумеется, это равенство выполняется, если существует каждый из входящих в него интегралов.

Вычисление определенного интеграла.

Понятие «определенный интеграл» было введено в математике для решения определенного класса задач , приводящих к необходимости вычисления  интегральных сумм  и их пределов. Однако, в дальнейшем была установлена связь между определенным и неопределенным интегралами.

Замена переменной интегрирования в определенном интеграле.

Пусть задан интеграл 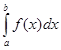, где f(x) – непрерывная функция на отрезке [a, b].

Введем новую переменную в соответствии с формулой x = j(t).

Тогда если:

1) j(t)- дифференцируемая  и j¢(t) непрерывна на отрезке [a, b];

2) отрезок [a, b] отображается на  [a, b];

3) j(a)  = а,   j(b) = b , то справедлива формула

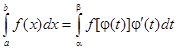
Тогда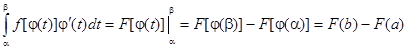

Пример 1. Вычислить определенный интеграл заменой переменной

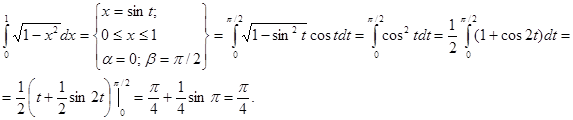
Пример 2. Вычислить определенный интеграл .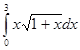

= = = = =.

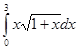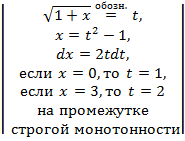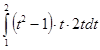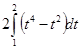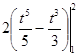При замене переменной в определенном интеграле следует помнить о том, что вводимая функция должна быть определена, непрерывна и дифференцируема  на отрезке интегрирования. В противном случае формальное применение формулы приводит к абсурду.

Пример 3. Найти .

.

Пример 4. Вычислим определенный интеграл двумя способами.

Очевидно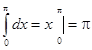, с другой стороны, если под знаком интеграла построить дробь, в знаменателе  ввести функцию тождественно равную единице и  применить формально тригонометрическую подстановку, то получим другой результат

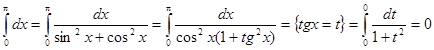
Т.е. два способа нахождения интеграла дают различные результаты. Это произошло из-за того, что не был учтен тот факт, что введенная  новая переменная t= tgx имеет на отрезке интегрирования разрыв (в точке х = p/2). Поэтому в данном случае такая подстановка неприменима. При замене переменной в определенном интеграле следует внимательно следить за выполнением перечисленных выше условий.

Интегрирование по частям.

Если функции u = j(x) и v = y(x) непрерывны и дифференцируемы на отрезке [a, b],  то справедлива формула интегрирования по частям:

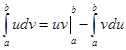
Вывод этой формулы аналогичен выводу формулы интегрирования по частям для неопределенного интеграла.

Пример 5. Вычислить интеграл .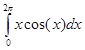

== = =

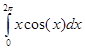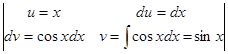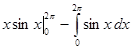=+ =0.

Интегрирование четной и нечетной функции по симметричному отрезку [-a,а].

Отметим следующие полезные свойства определенного интеграла.

Если f(x) четная функция, т.е. f(-x)=f(x), то .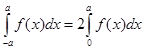

Если f(x) нечетная функция, т.е. f(-x)=-f(x), то .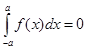

Приложения определенного интеграла.

Формула вычисления длины дуги кривой.

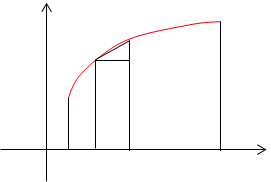
 Пусть плоская кривая АВ задана уравнением y= f(x),   где  f(x) непрерывная  на отрезке

[a, b] функция. Для нахождения длины кривой разобьем ее на n маленьких  кусочков ∆L_i  дуги. При большом числе разбиения дугу∆L_i можно спрямить кусочком прямой (хорды)  близкой по размеру.

                                                              Dy_i y            DL          y = f(x)

                                                                                      _i     

                                                                        a           Dx_i                     b        x

Тогда кривую АВ можно заменить ломанной кривой, построенной из прямых кусочков ∆L_i.и вписанной в эту кривую.

Длина ломаной линии, которая соответствует дуге, может быть найдена как .   Тогда длина дуги равна  L

Из геометрических соображений: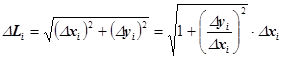

Тогда можно показать, что

Пример 1: Найти длину окружности, заданной уравнением x² + y² = a².

1 способ.  Выразим из уравнения переменную у:   - уравнение верхней половины окружности.

Найдем производную

и по формуле (15)  длину четверти окружности    

Тогда L = 2pa. Получили общеизвестную формулу длины окружности.

Формула вычисления объема фигуры вращения, образованной вращением линии вокруг координатной оси.

Пусть плоская кривая АВ задана уравнением y= f(x),   где  f(x) непрерывная  на отрезке

 [a, b] функция. Мысленно вращая линию вокруг оси ОX  или вокруг оси OYполучим поверхность вращения ограничивающий некоторый объем. Задача нахождения объема тела может решаться двумя способами.

Первый способ - вычисление объема тела по известным площадям его параллельных сечений.

Это универсальный метод, пригодный не только для фигур вращения.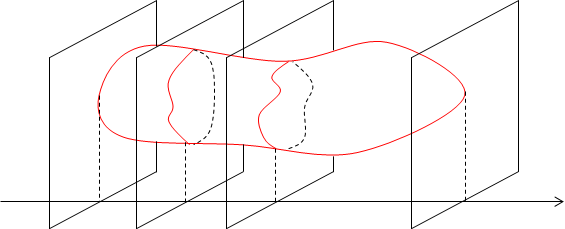

                                                       Q(x_i-1)                 Q(x_i)

                                   a                 x_i-1                   x_i                                              b                      x

Пусть имеется тело объема V. Предполагаем, что площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х_i разбиения отрезка [a, b]. Т.к. на каком - либо промежуточном отрезке разбиения [x_i-1, x_i] функция Q(x)( площадь сечения  как функция переменной x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно Q(x): M_i и m_i.

Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны M_iDx_i и m_iDx_i , здесь Dx_i = x_i - x_i-1.

Произведя такие построения для всех промежутков разбиения, получим цилиндры, сумма объемов которых равны соответственно  и (суммы Дарбу)

При стремлении к нулю шага разбиения l, эти суммы имеют общий предел:

=V

Таким образом, объем тела может быть найден по формуле:

Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма не просто  для сложных тел.

Пример 2. Найти объем шара радиуса R.

                                                                                   y

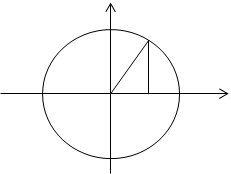
                                                                                 R       y

                                                           -R              0          x       R          x

В поперечных сечениях перпендикулярно оси ОХ шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле y=.

Тогда площадь окружности является функция от х и имеет вид: Q(x) = .

С помощью формулы (21) получаем объем шара:

.

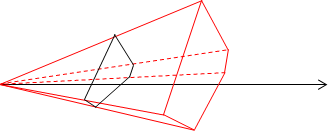
Пример 3: Найти объем произвольной пирамиды с высотой Н и площадью основания S.

                                                                            Q                            S

                                                                           x                     H                             x

            При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x/H, где х – расстояние от плоскости сечения до вершины пирамиды.

            Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.

Отсюда получаем функцию площадей сечений:

Находим объем пирамиды:

Второй способ – вычисление объема тел вращения.

Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке [a, b]. Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения.

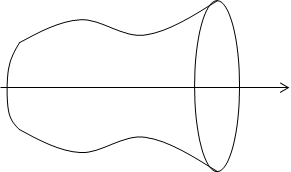                                                                       y = f(x)

                                                                                                                      x

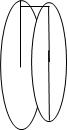
Для построения интегральной суммы  проведем разбиение отрезка [a, b] на кусочки Δx_i 

и через концы образовавшихся отрезков проведем плоскости перпендикулярно оси .

Т.к. каждое сечение тела плоскостью  x=ξ_i = const представляет собой круг радиуса   и его можно рассматривать как основание цилиндра  высотой Δx_i, то объем тела вращения может быть легко найден как предел суммы объемов цилиндров по полученной выше формуле:

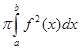
Пример 4. Вычислить объем тела, образованного вращением вокруг оси  кривой .

 Объем полученного тела вращения найдем по формуле:

.

Пример 5.

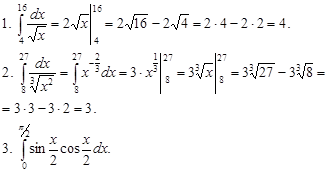
Воспользуемся формулой двойного угла синуса,  sin2α = 2sinαcosα:

   Почленно разделим числитель на знаменатель и, сократив дробь, найдем интеграл от суммы двух функций:

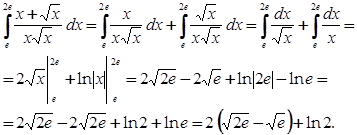
Методом замены переменной определенные интегралы решаются точно также как и неопределенные. Единственное различие заключается в том, что наряду с ведением новой переменной, заменяются также и пределы интегрирования.

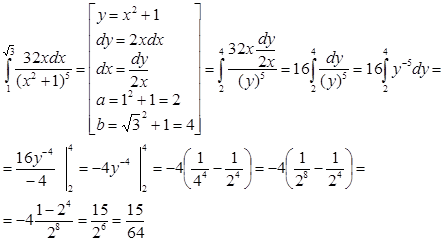
Вопросы для закрепления:

1. Определение  и обозначение определенного интеграла.

2. Сформулируйте геометрический смысл интегральной суммы и  определенного интеграла.

3. Сформулируйте теорему существования определенного интеграла.

4. Сформулируйте основные свойства определенного интеграла.

5. Сформулируйте теорему об оценке величины определенного интеграла.

6. Запишите теорему о среднем для определенного интеграла. Что такое среднее значение функции на интервале? Для каких функций теорема справедлива?

7. Выведите формулу Ньютона-Лейбница. В чем заключается сходство и различие определенного и неопределенного интегралов?

8. Сформулируйте и проиллюстрируйте на примерах методы вычисления определенных интегралов (непосредственное интегрирование, замены переменной, интегрирование по частям).

9. Дайте определение несобственного интеграла по бесконечному промежутку. В чем его геометрический смысл? Что означает сходимость несобственных интегралов 1-го рода?

10. Дайте определение несобственного интеграла от неограниченной функции. В чем его геометрический смысл? Как установить сходимость несобственных интегралов 2-го рода?

11. В чем заключается метод сравнения при выяснении сходимости несобственных интегралов?

12. Выведите формулы для вычисления площадей плоских фигур – ограниченных линиями заданными явно.

13. Выведите формулы для вычисления объемов тел вращения, по площади поперечного сечения тел.

14. Выведите формулы для вычисления длин дуг плоских кривых.

15. Какие физические задачи сводятся к вычислениям определенных? Приведите примеры.

Для подготовки к самостоятельной работе:

1.     Прочитать учебник О₃:  п. 11.1 – 11.16, стр.123.

2.     Выучить лекцию.

3.     Скачано с www.znanio.ru