Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 4. Интегральное исчисление и дифференциальные уравнения. Лекция № 9. Дифференциальные уравнения.

Раздел 4. Интегральное исчисление и дифференциальные уравнения.

Лекция № 9. Дифференциальные уравнения.(2 часа)

План лекции:

1. Примеры задач, приводящих к дифференциальным уравнениям.

2. Основные понятия и определения.

2.1 Обыкновенные дифференциальные уравнения. Основные определения. Свойства общего решения. Теорема Коши. Интегральные кривые. Особое решение.

2.2. Дифференциальные уравнения первого порядка. Уравнения вида у’ = f(х). Уравнения с разделяющимися переменными. Однородные уравнения. Уравнения, приводящиеся к однородным. Линейные уравнения. Линейные однородные дифференциальные уравнения. Линейные неоднородные дифференциальные уравнения. Метод Бернулли. Метод Лагранжа. Уравнение Бернулли.

2.3 Геометрическая интерпретация решений дифференциального уравнения первого порядка. Поле направлений. Изоклины.

2.4. Дифференциальные уравнения высших порядков. Уравнения, допускающие понижение порядка. Уравнения вида y⁽ⁿ⁾ = f(x). Уравнения, не содержащие явно искомой функции и ее производных до порядка n-1 включительно. Уравнения, не содержащие явно независимой переменной. Линейные дифференциальные уравнения высших порядков. Линейные однородные дифференциальные уравнения с произвольными коэффициентами. Линейные однородные дифференциальные уравнения с постоянными коэффициентами. Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.

Литература:

1.    Электронный ресурс. О_3: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440, п. 12.1 – 12.19, стр.197.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

ОК 02. Использовать современные средства поиска,  анализа и интерпретации информации и информационные технологии для выполнения задач профессиональной деятельности

З₃.Алгоритмы выполнения работ в профессиональной и смежных областях;

З₅.Структуру плана для решения задач;

З₆.Порядок оценки результатов решения задач профессиональной деятельности;

З₈. Приемы структурирования информации;

З₉. Формат оформления результатов поиска информации;

З₁₀. Современные средства и устройства информатизации; порядок их применения и программное обеспечение в профессиональной деятельности.

Основные понятия:

Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

Общим решением дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Решение вида у = j(х, С₀) называется частным решением дифференциального уравнения.

Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С₀), удовлетворяющего начальным условиям у(х₀) = у₀.

Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

Интегральной кривой называется график y = j(x) решения дифференциального уравнения  на плоскости ХОY.

Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши.) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.

Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:

.

Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде .

Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

Дифференциальное уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида  является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:  при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением. P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

Уравнением Бернулли называется уравнение вида  где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.

Производная y’ является угловым коэффициентом касательной к интегральной кривой.

Множество касательных в каждой точке рассматриваемой области называется полем направлений.

Линии равного наклона в поле направлений называются изоклинами.

Дифференциальным уравнением порядка n называется уравнение вида:

Нахождение решения уравнения , удовлетворяющего начальным условиям , называется решением задачи Коши.

Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных  вида:

 где p₀, p₁, …,p_n – функции от х или постоянные величины, причем p₀ ¹ 0.

Если f(x) = 0, то уравнение L(y) = 0 называется линейным однородным уравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p₀, p₁, p₂, … p_n – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.

1. ПРИМЕРЫ ЗАДАЧ, ПРИВОДЯЩИХ К ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ.

История дифференциальных уравнений.

     Теория ДУ возникла в конце XVII века под влиянием потребностей механики и других естественных наук. В самостоятельный раздел математики её выделил прежде всего Леонард Эйлер (1707-1783) -  гениальный математик, механик, физик.

     Долгие годы Эйлер работал в Петербургской Академии наук. Он оказал решающее влияние на развитие математики в Европе и во всем мире. Французский математик Пьер Лаплас считал Эйлера учителем математиков второй половины XVIII века. Но оценка Лапласа оказалась излишне скромной. История поставила Эйлера во главу математиков всех времен и народов.

      В Швейцарии, на родине Эйлера, полное собрание его научных трудов начали издавать в 1909 году, а завершили издание лишь в 1975 году. Список трудов Эйлера содержит 860 наименований.

     Леонард Павлович  (так его называли в России) был непревзойденным нескучным вычислителем. Неутолимо вычисляя при свечах, он потерял зрение сначала на правый, а затем и на левый глаз. Последние годы он не менее плодотворно работал слепым. На сегодня так и не издана большая часть из его 3000 писем.

      В 1971 году Швейцария украсила 10-франковые ассигнации портретом Л. Эйлера.

Задачи, приводящие к дифференциальным уравнениям.

Дифференциальное уравнение – основной математический аппарат в естествознании. Они применяются в физике, астрономии, аэродинамике и теории упругости, химии, экономике, биологии и медицине. Такой подход к изучению явлений природы впервые был предложен  итальянским ученным Г. Галилеем. Впервые его блестяще применил один из создателей математического анализа И. Ньютон.

Задачи, приводящие к обыкновенным дифференциальным уравнениям.

Решение задач методом математического моделирования сводится к отысканию неизвестной функции из уравнения, содержащего независимую переменную, искомую функцию и производные этой функции.

Существуют задачи, приводящие к дифференциальным уравнениям. Рассмотрим одну из них.

1.     Размножение бактерий. На опытах с бактериями установлено, что скорость размножения бактерий пропорциональна их количеству, если, конечно, для них имеется достаточный запас пищи.

Так как сами бактерии очень малы, а их количество велико, то можно считать, что масса бактерий с течением времени меняется непрерывно. Тогда скорость прироста массы бактерий называется скоростью размножения.

Если через число x(t) обозначить массу всех бактерий в момент времени t, то  будет скоростью размножения этих бактерий. Так как  скорость размножения  пропорциональна количеству бактерий, то существует постоянная k такая, что  = kx.              

По условию x(t) и x^/(t) неотрицательные, поэтому коэффициент k тоже неотрицательный.

Уравнение  = kx является простейшим примером дифференциального уравнения. Оно называется дифференциальным уравнением размножения. Искомым неизвестным уравнения (1) является функция x = x(t), которая в уравнение входит вместе со своей производной.

Решением данного уравнения является функция вида

x = Ce^kt, где С – const.

Действительно,

 = (Ce^kt) = С∙ e^kt ∙ k = k(Ce^kt) = kx.

2.                     Задача 1. Найти закон движения тела по оси Ox, если оно начало двигаться из точки М(4;0) со скоростью v = 2t + 3t².

При прямолинейном движении скорость есть производная от пути по времени. Обозначим путь через x, имеем v = ; тогда  = 2t + 3t². Получили дифференциальное уравнение.

3.                     Радиоактивный распад. Опытом установлено, что скорость распада радия в каждый момент времени пропорциональна начальному количеству радия.

Таким образом, если через x(t) обозначить массу вещества, еще не распавшегося к моменту времени t, то скорость распада   удовлетворяет уравнению:  = - kx(t), где k – некоторая положительная постоянная. . Знак минус показывает, что x(t) – убывающая функция, следовательно < 0.

Уравнение  = - kx(t) называется дифференциальным уравнением радиоактивного распада.

2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ.

2.1 Обыкновенные дифференциальные уравнения.

Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.

В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.

Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:

В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S.  Т.е.

Тогда получаем:  - уравнение связывает функцию f(t) с независимой переменной t и производной второго порядка функции f(t).

Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.

Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.

Пример 1.

 - обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается .

 - обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается

 - дифференциальное уравнение в частных производных первого порядка.

Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Свойства общего решения.

            1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.

            2) При каких- либо начальных условиях х = х₀, у(х₀) = у₀ существует такое значение С = С₀, при котором решением дифференциального уравнения является функция у = j(х, С₀).

Определение. Решение вида у = j(х, С₀) называется частным решением дифференциального уравнения.

Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = j(х, С₀), удовлетворяющего начальным условиям у(х₀) = у₀.

Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)

Если функция f(x, y) непрерывна в некоторой области  D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х₀, у₀) в области D, существует единственное решение  уравнения , определенное в некотором интервале, содержащем точку х₀, принимающее при х = х₀ значение j(х₀) = у₀, т.е. существует единственное решение дифференциального уравнения.

Определение. Интегралом дифференциального уравнения называется любое уравнение, не содержащее производных, для которого данное дифференциальное уравнение является следствием.

Пример 2.  Найти общее решение дифференциального уравнения .

Общее решение дифференциального уравнения ищется с помощью интегрирования  левой и правой частей уравнения, которое предварительно преобразовано следующим образом:

;      ;         

Теперь интегрируем:

 - это общее решение исходного дифференциального уравнения.

Допустим, заданы некоторые начальные условия: x₀ = 1; y₀ = 2, тогда имеем

При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).

Определение. Интегральной кривой называется график y = j(x) решения дифференциального уравнения  на плоскости ХОY.

Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши.) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.

Особые решения не зависят от постоянной С.

Особые решения нельзя получить из общего решения ни при каких значениях постоянной С.  Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.

Отметим, что не каждое дифференциальное уравнение имеет особые решения.

Пример 3. Найти общее решение дифференциального уравнения:  Найти особое решение, если оно существует.

         ®                          ®                ®

     ®                       ®         

Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0  можно получить из общего решения при С₁ = 0 ошибочно, ведь C₁ = e^C ¹ 0.

Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.

2.2 Дифференциальные уравнения первого порядка.

Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:

Если такое соотношение преобразовать к виду  то это дифференциальное уравнение первого порядка будет называться уравнением, разрешенным относительно производной.

Преобразуем такое выражение далее:

Функцию f(x,y) представим в виде:  тогда при подстановке в полученное выше уравнение  имеем:

- это так называемая дифференциальная форма уравнения первого порядка.

Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.

Уравнения вида y’ = f(x).

Пусть функция f(x) – определена и непрерывна на некотором интервале

a < x < b. В таком случае все решения данного дифференциального уравнения находятся как . Если заданы начальные условия х₀ и у₀, то можно определить постоянную С.

Уравнения с разделяющимися переменными

Определение. Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде

.

Такое уравнение можно представить также в виде:

Перейдем к новым обозначениям

Получаем:                                         

После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.

Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.

Пример 1. Найти общее решение дифференциального уравнения:

Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям):

- это  есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.

Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.

 - верно

Пример 2. Найти решение дифференциального уравнения  при условии у(2) = 1.

;   ®         ;     ®       ®

;   ®        

при у(2) = 1 получаем

Итого:    или  - частное решение;

Проверка:  , итого

 - верно.

Пример 3. Решить уравнение

   ®    ®  ®    ®  - общий интеграл

                                                                 - общее решение

Пример 4. Решить уравнение

Пример 5. Решить уравнение при условии у(1) = 0.

  ®  ®

Интеграл, стоящий в левой части будем брать по частям (см.  Интегрирование по частям).

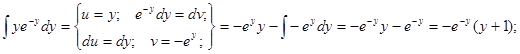
Если у(1) = 0, то

Итого, частный интеграл: .

Пример 6. Решить уравнение .

Для нахождения интеграла, стоящего в левой части уравнения см. Таблица основных интегралов. Получаем общий интеграл:

Пример 7. Решить уравнение

Преобразуем заданное уравнение:

  ®    ®    ® 

Получили общий интеграл данного дифференциального уравнения. Если из этого соотношения выразить искомую функцию у, то получим общее решение.

Пример 8. Решить уравнение .

;   

;          ;     

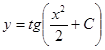
Допустим, заданы некоторые начальные условия х₀ и у₀. Тогда:

Получаем частное решение

Однородные уравнения.

Определение.  Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

Пример 9.   Является ли однородной функция 

Таким образом, функция f(x, y) является однородной 3- го порядка.

Определение. Дифференциальное уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида  является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

Рассмотрим однородное уравнение

Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:

Т.к. параметр t вообще говоря произвольный, предположим, что . Получаем:

Правая часть полученного равенства зависит фактически только от одного аргумента , т.е.

Исходное дифференциальное уравнение таким образом можно записать в виде:

Далее заменяем y = ux, .

 таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

Пример 10. Решить уравнение .

Введем вспомогательную функцию u.

.

Отметим, что введенная нами функция u всегда положительна, т.к. в противном случае теряет смысл исходное дифференциальное уравнение, содержащее .

Подставляем в исходное уравнение:

Разделяем переменные:

Интегрируя, получаем:

Переходя от вспомогательной функции обратно к функции у, получаем общее решение:

Уравнения, приводящиеся к однородным.

Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.

Это уравнения вида .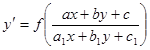

Если определитель  то переменные могут быть разделены подстановкой

где a и b - решения системы уравнений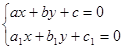

Пример 11. Решить уравнение

Получаем

Находим значение определителя .

Решаем систему уравнений

Применяем подстановку  в исходное уравнение:

Заменяем переменную  при подстановке в выражение, записанное выше, имеем:

Разделяем  переменные:

Переходим теперь к первоначальной функции у и переменной х.

Итого, выражение  является общим интегралом исходного дифференциального уравнения.

            В случае если в исходном уравнении вида 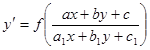 определитель  то переменные могут быть разделены подстановкой

Пример 12. Решить уравнение

Получаем

Находим значение определителя

Применяем подстановку

Подставляем это  выражение  в исходное уравнение:

Разделяем переменные:

Далее возвращаемся к первоначальной функции у и переменной х.

таким образом, мы получили общий интеграл исходного дифференциального уравнения.

Линейные уравнения.

Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.

            P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

Линейные однородные дифференциальные уравнения.

Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида

.

Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.

 Общее решение:                                   

Линейные неоднородные дифференциальные уравнения.

Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.

Метод Бернулли. (Якоб Бернулли (1654-1705) – швейцарский математик.)

Суть метода заключается в том, что искомая функция представляется в виде произведения двух функций  .

При этом очевидно, что  - дифференцирование по частям.

Подставляя в исходное уравнение, получаем:

Далее следует важное замечание – т.к. первоначальная функция была представлена нами в виде произведения, то каждый из сомножителей, входящих в это произведение, может быть произвольным, выбранным по нашему усмотрению.

Например, функция  может быть представлена как

 и т.п.

Таким образом, можно одну из составляющих произведение функций выбрать так, что выражение .

Таким образом, возможно получить функцию u, проинтегрировав, полученное соотношение как однородное дифференциальное уравнение по описанной выше схеме:

Для нахождения второй неизвестной функции v подставим поученное выражение для функции u в исходное уравнение  с учетом того, что выражение, стоящее в скобках, равно нулю.

Интегрируя, можем найти функцию v:

;             ;

Т.е. была получена вторая составляющая произведения , которое и определяет искомую функцию.

Подставляя полученные значения,  получаем:

Окончательно получаем формулу:

, где  С₂ - произвольный коэффициент.

Это соотношение может считаться решением неоднородного линейного дифференциального уравнения  в общем виде по способу Бернулли.

Метод Лагранжа.

 ( Ларганж Жозеф Луи (1736-1813) - французский математик,  през. Берлинской АН,

поч. чл. Пет. АН (1776)).

Метод Лагранжа  решения неоднородных линейных дифференциальных уравнений еще называют методом  вариации произвольной постоянной.

Вернемся к поставленной задаче:

Первый шаг данного метода состоит в отбрасывании правой части уравнения и замене ее нулем.

Далее находится решение получившегося однородного дифференциального уравнения:

.

Для того, чтобы найти соответствующее решение неоднородного дифференциального уравнения, будем считать постоянную С₁ некоторой функцией от х.

Тогда по правилам дифференцирования произведения  функций получаем:

Подставляем полученное соотношение в исходное уравнение

Из этого уравнения определим  переменную функцию С₁(х):

Интегрируя, получаем:

Подставляя это значение в исходное уравнение, получаем:

                                              .

Таким образом, мы получили результат, полностью совпадающий с результатом расчета по методу Бернулли.

При выборе метода решения линейных дифференциальных уравнений  следует руководствоваться  простотой интегрирования функций, входящих в исходный интеграл.

Далее рассмотрим примеры решения различных дифференциальных уравнений различными методами и сравним  результаты.

Пример 13.  Решить уравнение

Сначала приведем данное уравнение к стандартному виду:

Применим полученную выше формулу:

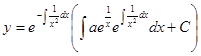
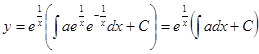
Уравнение Бернулли.

Определение. Уравнением Бернулли называется уравнение вида  где P и Q – функции от х или постоянные числа, а n – постоянное число, не равное 1.

Для решения уравнения Бернулли применяют подстановку , с помощью которой, уравнение Бернулли приводится к линейному.

Для этого разделим исходное уравнение на yⁿ.

Применим подстановку, учтя, что .

Т.е. получилось линейное уравнение относительно неизвестной функции z.

Решение этого уравнения будем искать в виде:

Пример 14.  Решить уравнение

Разделим уравнение на xy²: 

Полагаем

.

Полагаем

Произведя обратную подстановку, получаем:

Пример 15. Решить уравнение

Разделим обе части уравнения на

Полагаем

Получили линейное неоднородное дифференциальное уравнение. Рассмотрим соответствующее ему линейное однородное уравнение:

Полагаем C = C(x) и подставляем полученный результат в линейное неоднородное уравнение, с учетом того, что:

Получаем:

Применяя обратную подстановку, получаем окончательный ответ:

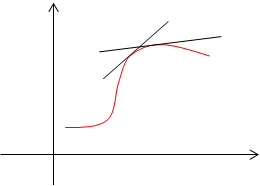
2.3. Геометрическая интерпретация решений дифференциальных уравнений первого порядка.

                                                             у                               a

                                                                                                           b

                                                                                    A                   S

                                                                                                                      x

Как уже говорилось выше (см. Интегральные кривые), линия S, которая задается функцией, являющейся каким- либо решением дифференциального уравнения, называется интегральной кривой уравнения

Производная y’ является угловым коэффициентом касательной к интегральной кривой.

В любой точке А(х, у) интегральной кривой этот угловой  коэффициент касательной может быть найден еще до решения дифференциального уравнения.

Т.к. касательная указывает направление интегральной кривой еще до ее непосредственного построения, то при условии непрерывности функции f(x, y) и непрерывного перемещения точки А можно наглядно изобразить поле направлений кривых, которые получаются в результате интегрирования дифференциального уравнения, т.е. представляют собой его общее решение.

Определение. Множество касательных в каждой точке рассматриваемой области называется полем направлений.

С учетом сказанного выше можно привести следующее геометрическое истолкование дифференциального уравнения:

            1) Задать дифференциальное уравнение первого порядка – это значит задать поле направлений.

            2) Решить или проинтегрировать дифференциальное уравнение – это значит найти всевозможные кривые, у которых направление касательных в каждой точке совпадает с полем направлений.

Определение. Линии равного наклона в поле направлений называются изоклинами.

2.4. Дифференциальные уравнения высших порядков.

Определение. Дифференциальным уравнением порядка n называется уравнение вида:

В некоторых случаях это уравнение можно разрешить относительно y⁽ⁿ⁾:

Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений.

Определение. Решение удовлетворяет начальным условиям , если

Определение. Нахождение решения уравнения , удовлетворяющего начальным условиям , называется решением задачи Коши.

Теорема Коши. (Теорема о необходимых и достаточных условиях существования решения задачи Коши).

Если функция (n-1) –й переменных вида в некоторой области D (n-1)- мерного пространства непрерывна и имеет непрерывные частные производные по , то какова бы не была точка () в этой области, существует единственное решение  уравнения , определенного в некотором интервале, содержащем точку х₀, удовлетворяющее начальным условиям .

Дифференциальные уравнения высших порядков, решение которых может быть найдено аналитически, можно разделить на несколько основных типов.

Рассмотрим подробнее методы нахождения решений этих уравнений.

Уравнения, допускающие понижение порядка.

Понижение порядка дифференциального уравнения – основной метод решения уравнений высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем уравнениям. Рассмотрим случаи, когда возможно понижение порядка.

Уравнения вида y⁽ⁿ⁾ = f(x).

Если f(x) – функция непрерывная на некотором промежутке a < x < b, то решение может быть найдено последовательным интегрированием.

Пример 1. Решить уравнение  с начальными условиями x₀ = 0; y₀ = 1;

Подставим начальные условия:

Получаем частное решение (решение задачи Коши): .

Ниже показана интегральная кривая данного дифференциального уравнения.

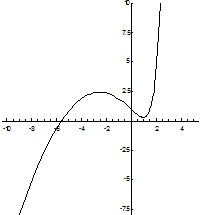
Уравнения, не содержащие явно искомой функции и ее производных до порядка k – 1 включительно.

Это уравнения вида:

В уравнениях такого типа возможно понижение порядка на k единиц. Для этого производят замену переменной:

Тогда получаем:

            Теперь допустим, что полученное дифференциальное уравнение проинтегрировано и совокупность его решений выражается соотношением:

Делая обратную подстановку, имеем:

Интегрируя полученное соотношение последовательно k раз, получаем окончательный ответ:

Пример 2. Найти общее решение уравнения .

Применяем подстановку

Произведя обратную замену, получаем:

Общее решение исходного дифференциального уравнения:

            Отметим, что это соотношение является решением для всех значений переменной х кроме значения х =0.

Уравнения, не содержащие явно независимой переменной.

            Это уравнения вида

Порядок таких уравнений может быть понижен на единицу с помощью замены переменных

 и т.д.

Подставляя эти значения в исходное дифференциальное уравнение, получаем:

Если это уравнение проинтегрировать, и - совокупность его решений, то для решения данного дифференциального уравнения остается решить уравнение первого порядка:

Пример 3. Найти общее решение уравнения

            Замена переменной:

            1)

Для решения полученного дифференциального уравнения произведем замену переменной:

            С учетом того, что , получаем:

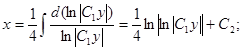
Общий интеграл имеет вид:

2)                

Таким образом, получили два общих решения.

Линейные дифференциальные уравнения высших порядков.

Определение. Линейным дифференциальным уравнением n – го порядка называется любое уравнение первой степени относительно функции у и ее производных  вида:

где p₀, p₁, …,p_n – функции от х или постоянные величины, причем p₀ ¹ 0.

Левую часть этого уравнения обозначим L(y).

Определение. Если f(x) = 0, то уравнение L(y) = 0 называется линейным однородным уравнением, если f(x) ¹ 0, то уравнение L(y) = f(x) называется линейным неоднородным уравнением, если все коэффициенты p₀, p₁, p₂, … p_n – постоянные числа, то уравнение L(y) = f(x) называется линейным дифференциальным уравнением высшего порядка с постоянными коэффициентами.

Отметим одно важное свойство линейных уравнений высших порядков, которое отличает их от нелинейных. Для нелинейных уравнений частный интеграл находится из общего, а для линейных – наоборот, общий интеграл составляется из частных. Линейные уравнения представляют собой наиболее изученный класс дифференциальных уравнений высших порядков. Это объясняется сравнительной простотой нахождения решения. Если при решении каких – либо практических задач требуется решить нелинейное дифференциальное уравнение, то часто применяются приближенные методы, позволяющие заменить такое уравнение “близким” к нему линейным.

Рассмотрим способы интегрирования некоторых типов линейных дифференциальных уравнений высших порядков.

Линейные однородные дифференциальные уравнения с произвольными коэффициентами.

Рассмотрим уравнение вида

Определение. Выражение  называется линейным дифференциальным оператором.

Линейный дифференциальный оператор обладает следующими свойствами:

            1)

            2)

Решения линейного однородного уравнения обладают следующими свойствами:

            1) Если функция у₁ является решением уравнения, то функция Су₁, где С – постоянное число, также является его решением.

            2) Если функции у₁ и у₂ являются решениями уравнения, то у₁ +у₂ также является его решением.

Структура общего решения.

Определение. Фундаментальной системой решений линейного однородного дифференциального уравнения n –го порядка на интервале (a, b) называется всякая система n линейно независимых на этом интервале решений уравнения.

Определение. Если из функций y_i составить определитель n – го порядка

,

то этот определитель называется определителем Вронского.

( Юзеф Вроньский (1776 – 1853) – польский математик и философ - мистик)

Теорема. Если функции  линейно зависимы, то составленный для них определитель Вронского равен нулю.

Теорема. Если функции линейно независимы, то составленный для них определитель Вронского не равен нулю ни в одной точке рассматриваемого интервала.

Теорема. Для того, чтобы система решений линейного однородного дифференциального уравнения  была фундаментальной необходимо и достаточно, чтобы составленный для них определитель Вронского был не равен нулю.

Теорема. Если  - фундаментальная система решений на интервале (a, b), то общее решение линейного однородного дифференциального уравнения является линейной комбинацией этих решений.

, где C_i –постоянные коэффициенты.

Применение приведенных выше свойств и теорем рассмотрим на примере линейных однородных дифференциальных уравнений второго порядка.

Общее решение линейного однородного дифференциального уравнения второго порядка.

Из вышеизложенного видно, что отыскание общего решения линейного однородного дифференциального уравнения сводится к нахождению его фундаментальной системы решений.

Однако, даже для уравнения второго порядка, если коэффициенты р зависят от х, эта задача не может быть решена в общем виде.

Тем не менее, если известно одно ненулевое частное решение, то задача может быть решена.

Теорема. Если задано уравнение вида  и известно одно ненулевое решение у = у₁, то общее решение может быть найдено по формуле:

Таким образом, для получения общего решения надо подобрать какое – либо частное решение дифференциального уравнения, хотя это бывает часто довольно сложно.

Линейные однородные дифференциальные уравнения с постоянными коэффициентами.

Решение дифференциального уравнения вида  или, короче,  будем искать в виде , где k = const.

Т.к.  то

При этом многочлен  называется характеристическим многочленом дифференциального уравнения.

Для того, чтобы функция  являлась решением исходного дифференциального уравнения, необходимо и достаточно, чтобы

 т.е.

Т.к. e^kx ¹ 0, то  - это уравнение называется характеристическим уравнением.

Как и любое алгебраическое уравнение степени n, характеристическое уравнение  имеет n корней. Каждому корню характеристического уравнения k_i соответствует решение дифференциального уравнения.

В зависимости от коэффициентов k характеристическое уравнение может иметь либо n различных действительных корней, либо среди действительных корней могут быть кратные корни, могут быть комплексно – сопряженные корни, как различные, так и кратные.

Не будем подробно рассматривать каждый случай, а сформулируем общее правило нахождения решения линейного однородного дифференциального уравнения с постоянными коэффициентами.

            1) Составляем характеристическое уравнение и находим его корни.

            2) Находим частные решения дифференциального уравнения, причем:

a) каждому действительному корню соответствует решение e^kx;

б) каждому действительному корню кратности m ставится в соответствие m решений:

в) каждой паре комплексно – сопряженных корней  характеристического уравнение ставится в соответствие два решения:

                                             и  .

г) каждой паре m – кратных комплексно – сопряженных корней  характеристического уравнения ставится в соответствие 2m решений:

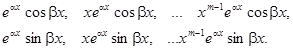
            3) Составляем линейную комбинацию найденных решений.

Эта линейная комбинация и будет являться общим решением исходного линейного однородного дифференциального уравнения с постоянными коэффициентами.

Пример 4. Решить уравнение .

Составим характеристическое уравнение:

Общее решение имеет вид: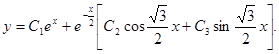

Пример 5. Решить уравнение

Это линейное однородное дифференциальное уравнение с переменными коэффициентами второго порядка. Для нахождения общего решения необходимо отыскать какое - либо частное решение.

Таким частным решением будет являться функция

Исходное дифференциальное уравнение можно преобразовать:

Общее решение имеет вид:

Окончательно:

Пример 6. Решить уравнение

Составим характеристическое уравнение:

Общее решение:

Пример 7. Решить уравнение

Характеристическое уравнение:

Общее решение:

Пример 8. Решить уравнение

Характеристическое уравнение:

Общее решение:

Пример 9. Решить уравнение

Характеристическое уравнение:

Общее решение:

Пример 10. Решить уравнение

Характеристическое уравнение:

Общее решение:

Пример 11. Решить уравнение

Характеристическое уравнение:

Общее решение:

Пример 12. Решить уравнение

Это уравнение не является линейным, следовательно, приведенный выше метод решения к нему неприменим.

Понизим порядок уравнения с помощью подстановки

Тогда

Окончательно получаем:

Это выражение будет общим решением исходного дифференциального уравнения. Полученное выше решение у₁ = С₁ получается из общего решения при С = 0.

Пример 13. Решить уравнение

Производим замену переменной:

Общее решение:

Линейные неоднородные дифференциальные уравнения с произвольными коэффициентами.

Рассмотрим уравнение вида

С учетом обозначения   можно записать:

При этом будем полагать, что коэффициенты и правая часть этого уравнения непрерывны на некотором интервале ( конечном или бесконечном).

Теорема. Общее решение линейного неоднородного дифференциального уравнения в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.

Доказательство.  Пусть Y – некоторое решение неоднородного уравнения.

Тогда при подстановке этого решения в исходное уравнение получаем тождество:

Пусть  - фундаментальная система решений линейного однородного уравнения . Тогда общее решение однородного уравнения можно записать в виде:

Далее покажем, что сумма является общим решением неоднородного уравнения.

Вообще говоря, решение Y может быть получено из общего решения, т.к. является частным решением.

Таким образом, в соответствии с доказанной теоремой, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким- то образом отыскать одно частное решение неоднородного уравнения. Обычно оно находится подбором.

На практике удобно применять метод вариации произвольных постоянных.

Для этого сначала находят общее решение соответствующего однородного уравнения в виде:

Затем, полагая коэффициенты C_i функциями от х, ищется решение неоднородного уравнения:

Можно доказать, что для нахождения функций C_i(x) надо решить систему уравнений:

Пример 14. Решить уравнение

Решаем линейное однородное уравнение

Решение неоднородного уравнения будет иметь вид:

Составляем систему уравнений:

Решим эту систему:

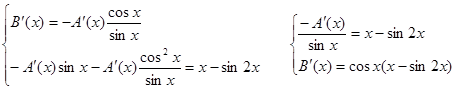
Из соотношения  найдем функцию А(х).

Теперь находим В(х).

Подставляем полученные значения в формулу общего решения неоднородного уравнения:

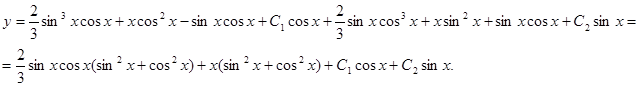
Окончательный ответ:

Таким образом, удалось избежать нахождения частного решения неоднородного уравнения методом подбора.

Вообще говоря, метод вариации произвольных постоянных пригоден для нахождения решений любого линейного неоднородного уравнения. Но т.к. нахождение фундаментальной системы решений соответствующего однородного уравнения может быть достаточно сложной задачей, этот метод в основном применяется для неоднородных уравнений с постоянными коэффициентами.

Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами.

Уравнения с правой частью специального вида.

Представляется возможным представить вид частного решения в зависимости от вида правой части неоднородного уравнения.

            Различают следующие случаи:

I.  Правая часть линейного неоднородного дифференциального уравнения имеет вид:

где - многочлен степени m.

            Тогда частное решение ищется в виде:

Здесь Q(x)- многочлен той же степени, что и P(x), но с неопределенными коэффициентами, а r – число, показывающее сколько раз число a является корнем характеристического уравнения для соответствующего линейного однородного дифференциального уравнения.

Пример 15. Решить уравнение .

Решим соответствующее однородное уравнение:

Теперь найдем частное решение исходного неоднородного уравнения.

Сопоставим правую часть уравнения с видом правой части, рассмотренным выше.

Частное решение ищем в виде: , где

Т.е.  

Теперь определим неизвестные коэффициенты А и В.

            Подставим частное решение в общем виде в исходное неоднородное дифференциальное уравнение.

Итого, частное решение:

Тогда общее решение линейного неоднородного дифференциального уравнения:

II.  Правая часть линейного неоднородного дифференциального уравнения имеет вид:

Здесь Р₁(х) и Р₂(х) – многочлены степени m₁ и m₂ соответственно.

Тогда частное решение неоднородного уравнения будет иметь вид:

где число r показывает сколько раз число  является корнем характеристического уравнения для соответствующего однородного уравнения, а Q₁(x) и Q₂(x) – многочлены степени не выше m, где m- большая из степеней m₁ и m₂.

Заметим, что если правая часть уравнения является комбинацией выражений рассмотренного выше вида, то решение находится как комбинация решений вспомогательных уравнений, каждое из которых имеет правую часть, соответствующую выражению, входящему в комбинацию.

            Т.е. если уравнение имеет вид: , то частное решение этого уравнения будет где  у₁ и у₂ – частные решения вспомогательных уравнений

 и

            Для иллюстрации решим рассмотренный выше пример другим способом.

Пример 16. Решить уравнение

Правую часть дифференциального уравнения представим в виде суммы двух функций f₁(x) + f₂(x) = x + (-sinx).

Составим и решим характеристическое уравнение:

1.      Для функции f₁(x) решение ищем в виде .

Получаем:  Т.е.   

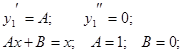
Итого:

2.      Для функции f₂(x) решение ищем в виде: .

Анализируя функцию f₂(x), получаем:

            Таким образом,

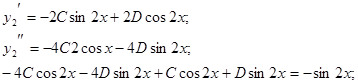
Итого:

            Т.е. искомое частное решение имеет вид:

Общее решение неоднородного дифференциального уравнения:

            Рассмотрим примеры применения описанных методов.

Пример 17. Решить уравнение

Составим характеристическое уравнение для соответствующего линейного однородного дифференциального уравнения:

Общее решение однородного уравнения:

Теперь найдем частное решение неоднородного уравнения в виде:

Воспользуемся методом неопределенных коэффициентов.

Подставляя в исходное уравнение, получаем:

Частное решение имеет вид:

Общее решение линейного неоднородного уравнения:

Пример 18. Решить уравнение 

Характеристическое уравнение:

Общее решение однородного уравнения:

Частное решение неоднородного уравнения: .

Находим производные и подставляем их в исходное неоднородное уравнение:

Получаем общее решение неоднородного дифференциального уравнения:

Вопросы для закрепления:

1      Понятие дифференциального уравнения.

2      Порядок  и степень дифференциального уравнения

3      Общее и частное решение дифференциального уравнения. Задача Коши.

4      Геометрическая интерпретация решения дифференциального уравнения.

5      Виды дифференциальных уравнений.

6      Понятие обыкновенных дифференциальных уравнений и их виды.

7      Дифференциальные уравнения первого порядка виды и методы решения.

8      Дифференциальные уравнения второго порядка виды и методы решения.

9      Дифференциальные уравнения с разделяющимися переменными.

10  Однородные дифференциальные уравнения.

11  Линейные  однородные  дифференциальные уравнения второго порядка с постоянными коэффициентами.

Для подготовки к самостоятельной работе:

1.        Прочитать учебник О₃: п. 12.1 – 12.19, стр. 167.

2.        Выучить лекцию.

3.        Подготовиться к тестированию по пройденному материалу.

Скачано с www.znanio.ru