Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 3. Введение в анализ. Дифференциальные исчисления. Лекция № 6. Производная и дифференциал.

Раздел 3. Введение в анализ. Дифференциальные исчисления.

Лекция № 6. Производная и дифференциал. (2 часа)

План лекции:

1. Производная функции. Первый дифференциал функции, связь с приращением функции. Основные правила дифференцирования. Производные и дифференциалы высших порядков.

2. Возрастание и убывание функций. Экстремумы функций.

3. Частные производные функции нескольких переменных. Полный дифференциал. Частные производные высших порядков.

Литература:

1.    Электронный ресурс. О_2: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 2: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 241 с. — (Профессиональное образование). — ISBN 978-5-534-10173-7. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442439, п. 7.1 – 7.14, 8.1 – 8.15, стр.90.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

З₂.Основные источники информации и ресурсы для решения задач и проблем в профессиональном и/или социальном контексте;

З₅.Структуру плана для решения задач;

З₆.Порядок оценки результатов решения задач профессиональной деятельности.

Основные понятия:

Производной функции  в точке  называется предел отношения приращения функции  к приращению аргумента Dх, когда →0.

Механический смысл производной: скорость прямолинейного движения материальной точки в момент времени t₀ есть производная пути по времени.

Геометрический смысл производной:  тангенс угла наклона касательной к графику функции y=f(x) в точке с абсциссой x₀ равен производной функции f(x) в точке x_0.

Уравнение касательной к кривой:                                            

Нормаль к кривой в точке М₀ – прямая проходящая через точку М₀, перпендикулярно касательной к кривой в этой точке. Из условия перпендикулярности прямых  угловой коэффициент нормали равен .

 Уравнение нормали к кривой: .                                    

 Пусть задана функция , где . Тогда у есть сложная функция от х, т.е. , и переменная и – промежуточный аргумент.

Правило дифференцирования сложной функции: производная сложной функции равна произведению производной функции по промежуточной переменной на производную промежуточной переменной по независимой переменной.

Производная обратной функции обратна по величине производной данной функции.

Производная п-го порядка является производной от производной (п-1) порядка, т.е.   .

Пусть даны две функции  и  одной независимой переменной t, определённые и непрерывные в одном и том же промежутке. Если  строго монотонна, то обратная к ней функция  однозначна, также непрерывна и строго монотонна. Поэтому у можно рассматривать как функцию, зависящую от переменной х, которая в свою очередь зависит от переменной t, называемой параметром:

В этом случае говорят, что функция у от х задана параметрически с помощью уравнений  .

Если функция задана уравнением , разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения , не разрешённого относительно у.

Функция y=f(x) возрастает на интервале X, если для любых  и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Функция y=f(x) убывает на интервале X, если для любых  и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

Точку x₀ называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку x₀ называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

Функция двух переменных обычно записывается как , при этом переменные x, y называются независимыми переменными или аргументами.

Частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.

Полный дифференциал первого порядка функции двух переменных имеет вид:

Полный дифференциал второго порядка: .

1.      Производная функции. Первый дифференциал функции, связь с приращением функции. Основные правила дифференцирования. Производные и дифференциалы высших порядков.

Источником дифференциального исчисления были два вопроса, выдвинутые запросами науки и техники в 17 веке.

1)        Вопрос о вычислении скорости при произвольно заданном законе движения.

2)        Вопрос о нахождении (с помощью вычислений) касательной к кривой произвольно заданной.

Задачу проведения касательной к некоторым кривым решил ещё древнегреческий учёный Архимед (287-212 г.г. до н.э.), пользуясь методом вычерчивания.

Но только в 17 и 18 веках в связи с прогрессом естествознания и техники эти вопросы получили должное развитие.

Одним из важных вопросов при изучении любого физического явления обычно является вопрос о скорости, быстроте происходящего явления.

Скорость с которой движется самолёт или автомобиль, всегда служит важнейшим показателем его работы. Быстрота прироста населения того или иного государства является одной из основных характеристик его общественного развития.

Первоначальная идея скорости ясна каждому. Однако для решения большинства практических задач этой общей идеи недостаточно. Необходимо иметь такое количественное определение этой величины, которую мы называем скоростью. Потребность в таком точном количественном определении исторически послужила одним из основных побудителей к созданию математического анализа. Целый раздел математического анализа посвящен решению этой основной задачи и выводам из этого решения. К изучению этого раздела мы и переходим.

Определение производной, её геометрический смысл.

Пусть задана функция f(x) на интервале (a, b), которая непрерывна в нем. Зафиксируем точку x внутри (a, b), MP секущая.

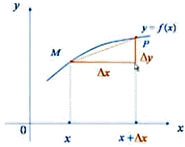
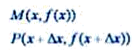
1. Дадим аргументу х приращение Dх, тогда функция получит приращение :          

Df(x)=f(x+Dх)

2. Составим отношение:     .

3. Переходя к пределу в  при  и, предполагая, что предел существует, получим величину , которую называют производной функции  по аргументу х.

Определение. Производной функции  в точке  называется предел отношения приращения функции  к приращению аргумента Dх, когда →0.

Значение производной, очевидно, зависит от точки х, в которой оно найдено, поэтому производная функции  есть в свою очередь некоторая функция от х. Обозначается .

По определению имеем

                      или                                            

Пример. Найти производную функции .

1. ;

2.

3.

4. . Итак .

Механический смысл производной:

 скорость прямолинейного движения материальной точки в момент времени t₀ есть производная пути по времени

Геометрический смысл производной:

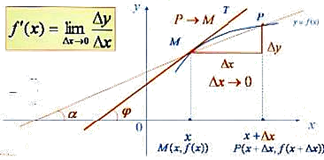
По определению  устремим точку M к точке P , это эквивалентно стремлению .

Предельное положение секущей MP это касательная к кривой в точке M , ее угловой коэффициент равен:

Следовательно, производная в точке х равна тангенсу угла наклона касательной в этой точке.

тангенс угла наклона касательной к графику функции y=f(x) в точке с абсциссой x₀ равен производной функции f(x) в точке x₀

Уравнение касательной к кривой:                                            

Нормаль к кривой в точке М₀ – прямая проходящая через точку М₀, перпендикулярно касательной к кривой в этой точке. Из условия перпендикулярности прямых  угловой коэффициент нормали равен ,

Уравнение нормали к кривой: .                                    

Дифференциал функции

Пусть задана y = f(x) на интервале (a, b). Функция y = f(x) называется дифференцируемой в точке x, если ∆y можно представить с помощью следующего выражения:

∆y = A∆x + α(∆)∆x

где А= const при фиксированном х и  при

Теорема. Для дифференцируемости функции в точке х необходимо и достаточно, чтобы функция имела в этой точке конечную производную.

Дифференциалом функции y = f(x) называется выражение вида dy=A∆x - это главная линейная часть приращения ∆y , на основании предыдущей теоремы, обозначив дифференциал независимой переменной через dx=∆x, получим выражение для дифференциала:

Геометрический смысл дифференциала виден из следующего рисунка

, т.е. дифференциал функции равен отрезку PQ это приращение ординаты касательной, а приращение ∆y это отрезок

Применение дифференциалов в приближенных вычислениях

Вычислить:

Используем приближенное равенство

Основные правила дифференцирования.

Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.

1) (u ± v)¢ = u¢ ± v¢

2) (u×v)¢ = u×v¢ + u¢×v

3), если v ¹ 0

Производные основных элементарных функций.

1)С¢  = 0;                                            9)

2)(x^m)¢ = mx^m-1;                              10)

3)                        11)

4)                         12)

5)                                        13)

6)                                14) 

7)                                        15)

8)                                16) 

Производная сложной функции.

Пусть задана функция , где . Тогда у есть сложная функция от х, т.е. , и переменная и – промежуточный аргумент. Тогда справедлива теорема.

Теорема. Если функция  u = g(x) имеет производную , а функция y = f(и) имеет производную , то сложная функция   имеет производную , или .

Доказательство.  Дадим аргументу х приращение , тогда u = g(x) и  получат соответственно приращения  и . Предположим, что если  и , тогда имеет место тождество

Перейдём к пределу в последнем тождестве, получим:

,

( с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция), то , откуда , что и требовалось доказать.

Из теоремы вытекает правило дифференцирования сложной функции: производная сложной функции равна произведению производной функции по промежуточной переменной на производную промежуточной переменной по независимой переменной.

Производная обратной функции.

Пусть требуется найти производную функции у = f(x) при условии, что обратная ей функция x=φ(y) имеет производную, отличную от нуля в соответствующей точке.

Для решения этой задачи дифференцируем функцию  x = φ(y) по х:

 , следовательно , или , тогда

  или   ч.т.д.

т.е. производная обратной функции обратна по величине производной данной функции.

Пример. Найти формулу для производной функции arctgх.

Функция arctgх является функцией, обратной функции tgх, т.е. ее производная может быть найдена следующим образом:

Известно, что  

По приведенной выше формуле получаем:

Т.к.  то можно записать окончательную формулу для производной арктангенса:

Таким образом получены все формулы для производных арксинуса, арккосинуса и других обратных функций, приведенных в таблице производных.

Производные высших порядков.

Как уже отмечалось, производная  функции  сама является некоторой функцией её аргумента х. Следовательно, по отношению к ней снова можно ставить вопрос о существовании и нахождении производной. Назовём  производной первого порядка функции .

Производная от производной некоторой функции называется производной второго порядка (или второй производной) этой функции. Производная от второй производной называется производной третьего порядка (или третьей производной) и т. д. Производные, начиная со второй, называются производными высших порядков и обозначаются

Производная п-го порядка является производной от производной (п-1) порядка, т.е.   .

Пример.  Найти производную п-го порядка от функции .

Производные высших порядков имеют широкое применение в физике. Если функция  описывает закон движения материальной точки по прямой линии, то первая производная  есть мгновенная скорость точки в момент времени , а вторая производная равна скорости изменения скорости, т.е. ускорению движущейся точки в этот момент, т.е., .

Параметрически заданные функции и неявно.

а) параметрически заданная функция

Пусть даны две функции  и  одной независимой переменной t, определённые и непрерывные в одном и том же промежутке. Если  строго монотонна, то обратная к ней функция  однозначна, также непрерывна и строго монотонна. Поэтому у можно рассматривать как функцию, зависящую от переменной х, которая в свою очередь зависит от переменной t, называемой параметром:

В этом случае говорят, что функция у от х задана параметрически с помощью уравнений  .

Параметрическое задание функции имеет важное значение при изучении движения точки. Если точка движется на плоскости, то её координаты х,у являются функциями времени t. Задав эти функции , , мы полностью определим движение точки. Для каждого промежутка времени в котором функция  строго монотонна, можно определить функцию , графиком которой является кривая, описываемая за этот промежуток времени движущейся точкой, т.е. траектория движения.

б) неявно заданная функция

Если функция задана уравнением , разрешенным относительно у, то функция задана в явном виде (явная функция).

Под неявным заданием функции понимают задание функции в виде уравнения , не разрешённого относительно у.

Всякую явно заданную функцию  можно записать как неявно заданную уравнением , но не наоборот.

Не всегда легко, а иногда и невозможно разрешить уравнение относительно у, например  или .

Дифференцирование функций, заданных параметрически и неявно.

Предположим, что функции  и  имеют производные, причём  на некотором промежутке. Отсюда вытекает строгая монотонность функции  и, следовательно, однозначность обратной функции . По теореме о производной обратной функции, функция  имеет производную , а функция  по теореме о производной сложной функции имеет производную . Следовательно,   или  .

Выведенная формула даёт возможность находить производную  от функции, заданной параметрически, не находя выражения непосредственной зависимости у от х.

Пример.   Пусть     Найти .

Решение: имеем , , следовательно , т.е. .

В этом можно убедиться, найдя непосредственно зависимость у от х. Действительно, . Тогда . Отсюда , т.е. .

Если функция задана в неявном виде , то для нахождения производной от у по х нет необходимости разрешать уравнение относительно у: достаточно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно .

Производная неявной функции выражается через аргумент х и функцию у.

Пример. Найти производную функции, заданную уравнением .

Решение. Функция у задана неявно. Дифференцируем по х равенство . Из полученного соотношения

следует, что , т.е. .

2.      Возрастание и убывание функций. Экстремумы функций.

Определение возрастающей функции.

Функция y=f(x) возрастает на интервале X, если для любых  и выполняется неравенство . Другими словами – большему значению аргумента соответствует большее значение функции.

Определение убывающей функции.

Функция y=f(x) убывает на интервале X, если для любых  и выполняется неравенство . Другими словами – большему значению аргумента соответствует меньшее значение функции.

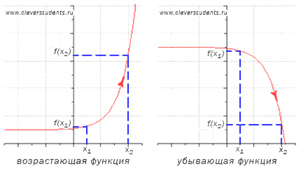
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b), то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.

К примеру, из свойств основных элементарных функций мы знаем, что y=sinx определена и непрерывна для всех действительных значений аргумента. Поэтому, из возрастания функции синуса на интервале  мы можем утверждать о возрастании на отрезке .

Достаточные условия возрастания и убывания функции.

На основании достаточных условий (признаков) возрастания и убывания функции находятся промежутки возрастания и убывания функции.

Вот формулировки признаков возрастания и убывания функции на интервале:

·            если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;

·            если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

·            найти область определения функции;

·            найти производную функции;

·            решить неравенства  и  на области определения;

·            к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Рассмотрим пример нахождения промежутков возрастания и убывания функции для разъяснения алгоритма.

Пример.

Найти промежутки возрастания и убывания функции .

Решение.

На первом шаге нужно найти область определения функции. В нашем примере выражение в знаменателе не должно обращаться в ноль, следовательно, .

Переходим к нахождению производной функции:

Для определения промежутков возрастания и убывания функции по достаточному признаку решаем неравенства  и  на области определения. Воспользуемся обобщением метода интервалов. Единственным действительным корнем числителя является x = 2, а знаменатель обращается в ноль при x=0. Эти точки разбивают область определения на интервалы, в которых производная функции сохраняет знак. Отметим эти точки на числовой прямой. Плюсами и минусами условно обозначим интервалы, на которых производная положительна или отрицательна. Стрелочки снизу схематично показывают возрастание или убывание функции на соответствующем интервале.

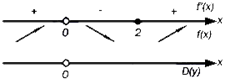
Таким образом, 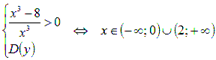 и .

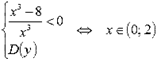В точке x=2 функция определена и непрерывна, поэтому ее следует добавить и к промежутку возрастания и к промежутку убывания. В точке x=0 функция не определена, поэтому эту точку не включаем в искомые интервалы.

Приводим график функции для сопоставления с ним полученных результатов.

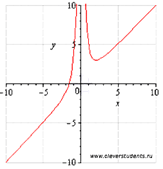
Ответ: функция возрастает при , убывает на интервале (0;2].

Точку x₀ называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке максимума называют максимумом функции и обозначают .

Точку x₀ называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции и обозначают .

Под окрестностью точки x₀ понимают интервал , где  - достаточно малое положительное число.

Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.

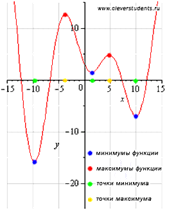
Не путайте экстремумы функции с наибольшим и наименьшим значением функции.

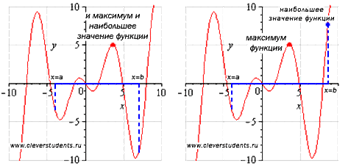
На первом рисунке наибольшее значение функции на отрезке [a; b] достигается в точке максимума и равно максимуму функции, а на втором рисунке – наибольшее значение функции достигается в точке x=b, которая не является точкой максимума.

Достаточные условия экстремума функции.

Для нахождения максимумов и минимумов функции можно пользоваться любым из трех признаков экстремума, конечно, если функция удовлетворяет их условиям. Самым распространенным и удобным является первый из них.

Первое достаточное условие экстремума.

Пусть функция y=f(x) дифференцируема в -окрестности точки x₀, а в самой точке x₀ непрерывна.

Тогда

• если  при  и  при , то x₀ - точка максимума;
• если  при  и  при , то x₀ - точка минимума.

Другими словами:

·        если в точке x₀ функция непрерывна и в ней производная меняет знак с плюса на минус, то x₀ - точка максимума;

·        если в точке x₀ функция непрерывна и в ней производная меняет знак с минуса на плюс, то x₀ - точка минимума.

Алгоритм нахождения точек экстремума по первому признаку экстремума функции.

·        Находим область определения функции.

·        Находим производную функции на области определения.

·        Определяем нули числителя, нули знаменателя производной и точки области определения, в которых производная не существует (все перечисленные точки называют точками возможного экстремума, проходя через эти точки, производная как раз может изменять свой знак).

·        Эти точки разбивают область определения функции на промежутки, в которых производная сохраняет знак. Определяем знаки производной на каждом из интервалов (например, вычисляя значение производной функции в любой точке отдельно взятого интервала).

·        Выбираем точки, в которых функция непрерывна и, проходя через которые, производная меняет знак - они и являются точками экстремума.

Пример.

Найти экстремумы функции .

Решение.

Областью определения функции является все множество действительных чисел, кроме x=2.

Находим производную:

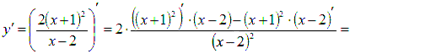
Нулями числителя являются точки x=-1 и x=5, знаменатель обращается в ноль при x=2. Отмечаем эти точки на числовой оси

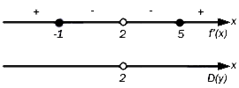
Определяем знаки производной на каждом интервале, для этого вычислим значение производной в любой из точек каждого интервала, например, в точках x=-2, x=0, x=3 и x=6.

, следовательно, на интервале  производная положительна (на рисунке ставим знак плюс над этим интервалом). Аналогично

Поэтому над вторым интервалом ставим минус, над третьим – минус, над четвертым – плюс.

Осталось выбрать точки, в которых функция непрерывна и ее производная меняет знак. Это и есть точки экстремума.

В точке x=-1 функция непрерывна и производная меняет знак с плюса на минус, следовательно, по первому признаку экстремума, x=-1 – точка максимума, ей соответствуем максимум функции .

В точке x=5 функция непрерывна и производная меняет знак с минуса на плюс, следовательно, x=-1 – точка минимума, ей соответствуем минимум функции .

Графическая иллюстрация.

Ответ: .

Второй признак экстремума функции.

Пусть ,

• Если , то  - точка минимума;
• Если , то  - точка максимума.

Как видите, этот признак экстремума функции требует существования производной как минимум до второго порядка в точке .

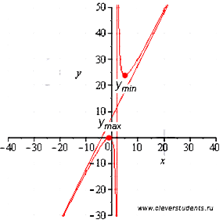
Пример. Найти экстремумы функции .

Решение.

Начнем с области определения:

Продифференцируем исходную функцию:

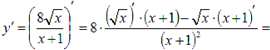
Производная обращается в ноль при x=1, то есть, это точка возможного экстремума.

Находим вторую производную функции и вычисляем ее значение при x = 1:

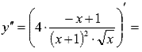
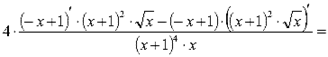
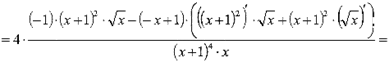
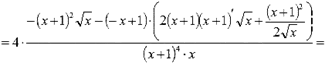
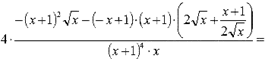
Следовательно, по второму достаточному условию экстремума, x=1 - точка максимума. Тогда  - максимум функции.

Графическая иллюстрация.

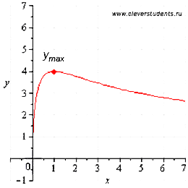
Ответ: .

Третье достаточное условие экстремума функции.

Пусть функция y=f(x) имеет производные до n-ого порядка в -окрестности точки  и производные до n+1-ого порядка в самой точке . Пусть  и .

Тогда,

• если n – четное, то  - точка перегиба;
• если n – нечетное, то  - точка экстремума, причем
• если , то  - точка минимума;
• если , то  - точка максимума.

Пример. Найти точки экстремума функции .

Решение.

Исходная функция является целой рациональной, ее областью определения является все множество действительных чисел.

Продифференцируем функцию:

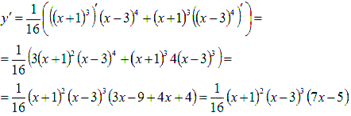
Производная обращается в ноль при , следовательно, это точки возможного экстремума. Воспользуемся третьим достаточным условием экстремума.

Находим вторую производную и вычисляем ее значение в точках возможного экстремума (промежуточные вычисления опустим):

Следовательно,  - точка максимума (для третьего достаточного признака экстремума имеем n=1 и ).

Для выяснения характера точек  находим третью производную и вычисляем ее значение в этих точках:

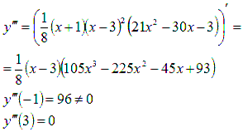
Следовательно,  - точка перегиба функции (n=2 и ).

Осталось разобраться с точкой . Находим четвертую производную и вычисляем ее значение в этой точке:

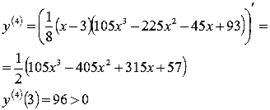
Следовательно,  - точка минимума функции.

Графическая иллюстрация.

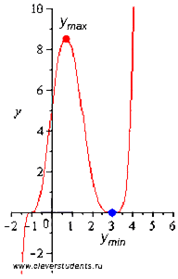
Ответ:  - точка максимума,  - точка минимума функции.

3.      Частные производные функции нескольких переменных. Полный дифференциал. Частные производные высших порядков.

Функция двух переменных обычно записывается как , при этом переменные x, y называются независимыми переменными или аргументами.

Пример:  – функция двух переменных.

Иногда используют запись . Также встречаются задания, где вместо буквы  используется буква .

С геометрической точки зрения функция двух переменных  чаще всего представляет собой поверхность трехмерного пространства (плоскость, цилиндр, шар, параболоид, гиперболоид и т. д.).

Переходим к вопросу нахождения частных производных первого и второго порядков. Частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.

Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций. Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас:

Пример 1. Найти частные производные первого и второго порядка функции

Сначала найдем частные производные первого порядка. Их две.

Обозначения:
 или  – частная производная по «икс»
 или  – частная производная по «игрек»

Начнем с . Когда мы находим частную производную по «икс», то переменная считается константой (постоянным числом).

Решаем:

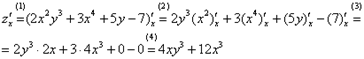
Комментарии к выполненным действиям:

(1) Первое, что мы делаем при нахождении частной производной – заключаем всю функцию в скобки под штрих с подстрочным индексом.

Внимание, важно! Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если вы где-нибудь нарисуете «штрих» без , то преподаватель, как минимум, может поставить рядом с заданием .

(2) Используем правила дифференцирования , . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как  считается константой, а любую константу можно вынести за знак производной, то  мы выносим за скобки. То есть в данной ситуации  ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как  константа, то  – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».

(3) Используем табличные производные  и .

(4) Упрощаем ответ.

Теперь . Когда мы находим частную производную по «игрек», то переменная  считается константой (постоянным числом).

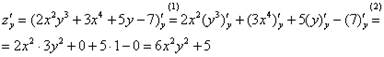
(1) Используем те же правила дифференцирования , . В первом слагаемом выносим константу  за знак производной, во втором слагаемом ничего вынести нельзя поскольку  – уже константа.

(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица равно справедлива и для (да и вообще почти для любой буквы). В частности, используемые нами формулы выглядят так:  и .

В чём смысл частных производных?

По своей сути частные производные 1-го порядка напоминают «обычную» производную:

 – это функции, которые характеризуют скорость изменения функции  в направлении осей  и  соответственно. Так, например, функция  характеризует крутизну «подъёмов» и «склонов» поверхности  в направлении оси абсцисс, а функция  сообщает нам о «рельефе» этой же поверхности в направлении оси ординат.

! Примечание: здесь подразумеваются направления, которые параллельны координатным осям.

В целях лучшего понимания рассмотрим конкретную точку  плоскости  и вычислим в ней значение функции («высоту»):
 – а теперь представьте, что вы здесь находитесь (НА САМОЙ поверхности).

Вычислим частную производную по «икс» в данной точке:

Отрицательный знак «иксовой» производной сообщает нам об убывании функции   в точке  по направлению оси абсцисс. Иными словами, если мы сделаем маленький-маленький (бесконечно малый) шажок в сторону острия оси  (параллельно данной оси), то спустимся вниз по склону поверхности.

Теперь узнаем характер «местности» по направлению оси ординат:

Производная по «игрек» положительна, следовательно, в точке  по направлению оси  функция  возрастает. Если совсем просто, то здесь нас поджидает подъём в гору.

Кроме того, частная производная в точке характеризует скорость изменения функции по соответствующему направлению. Чем полученное значение больше по модулю – тем поверхность круче, и наоборот, чем оно ближе к нулю – тем поверхность более пологая. Так, в нашем примере «склон» по направлению оси абсцисс более крут, чем «гора» в направлении оси ординат.

Но то были два частных пути. Совершенно понятно, что из точки, в которой мы находимся, (и вообще из любой точки данной поверхности) мы можем сдвинуться и в каком-нибудь другом направлении. Таким образом, возникает интерес составить общую «навигационную карту», которая сообщала бы нам о «ландшафте» поверхности  по возможности в каждой точке  области определения данной функции по всем доступным путям.

Систематизируем элементарные прикладные правила:

1) Когда мы дифференцируем по , то переменная  считается константой.

2) Когда же дифференцирование осуществляется по , то константой считается .

3) Правила и таблица производных элементарных функций справедливы и применимы для любой переменной (,  либо какой-нибудь другой), по которой ведется дифференцирование.

Шаг второй. Находим частные производные второго порядка. Их четыре.

Обозначения:
 или  – вторая производная по «икс»
 или  – вторая производная по «игрек»
 или  – смешанная производная «икс по игрек»
 или  – смешанная производная «игрек по икс»

Со второй производной нет никаких проблем. Говоря простым языком, вторая производная – это производная от первой производной.

Для удобства я перепишу уже найденные частные производные первого порядка:

Сначала найдем смешанные производные:

Как видите, всё просто: берем частную производную  и дифференцируем ее еще раз, но в данном случае – уже по «игрек».

Аналогично:

В практических примерах можно ориентироваться на следующее равенство:

Таким образом, через смешанные производные второго порядка очень удобно проверить, а правильно ли мы нашли частные производные первого порядка.

Находим вторую производную по «икс».
Никаких изобретений, берем  и дифференцируем её по «икс» еще раз:

Аналогично:

Следует отметить, что при нахождении ,  нужно проявить повышенное внимание, так как никаких чудесных равенств для их проверки не существует.

Вторые производные также находят широкое практическое применение, в частности, они используются в задаче отыскания экстремумов функции двух переменных. Но всему своё время:

Пример 2. Найти частные производные первого порядка функции . Проверить, что . Записать полный дифференциал первого порядка .

Решение: Находим частные производные первого порядка:

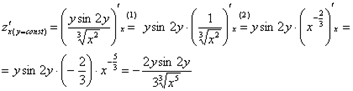
Обратите внимание на подстрочный индекс: , рядом с «иксом» не возбраняется в скобках записывать, что  – константа. Данная пометка может быть очень полезна для начинающих, чтобы легче было ориентироваться в решении.

Дальнейшие комментарии:

(1) Выносим все константы за знак производной. В данном случае  и , а, значит, и их произведение  считается постоянным числом.

(2) Не забываем, как правильно дифференцировать корни.

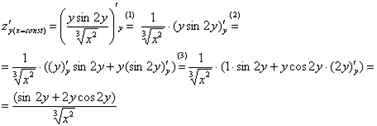
(1) Выносим все константы за знак производной, в данной случае константой является .

(2) Под штрихом у нас осталось произведение двух функций, следовательно, нужно использовать правило дифференцирования произведения .

(3) Не забываем, что  – это сложная функция (хотя и простейшая из сложных). Используем соответствующее правило: .

Теперь находим смешанные производные второго порядка:

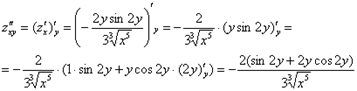
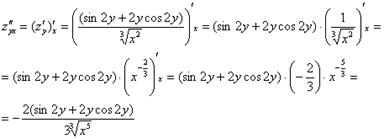
, значит, все вычисления выполнены верно.

Запишем полный дифференциал .

Полный дифференциал первого порядка функции двух переменных имеет вид:

В данном случае:

То есть, в формулу нужно просто подставить уже найденные частные производные первого порядка. Значки дифференциалов  и  в этой и похожих ситуациях по возможности лучше записывать в числителях:

Полный дифференциал второго порядка.

Он выглядит так:

найдём «однобуквенные» производные 2-го порядка:

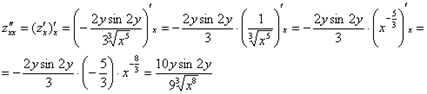
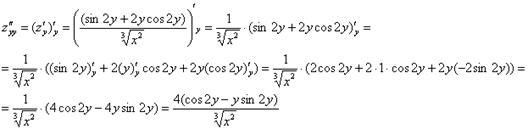
и запишем «монстра», аккуратно «прикрепив» квадраты , произведение  и не забыв удвоить смешанную производную:

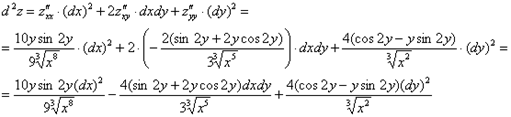
Вопросы для закрепления:

1.        Дать определение функции.

2.        Что такое область определения функции?

3.        Что такое область значений функции?

4.        Как исследовать функцию на четность?

5.        Что называется пределом функции в точке?

6.        Что называется пределом функции на бесконечности?

7.        Каковы основные свойства пределов.

8.        Что такое приращение функции и аргумента?

9.        Что называется производной функции?

10.    В чем состоит физический смысл производной?

11.    В чем состоит геометрический смысл производной?

12.    Чему равен дифференциал функции?

13.    Что называется дифференциалом аргумента?

14.    В чем состоит геометрический смысл дифференциала функции?

15.    Понятие возрастания (убывания) функции. Алгоритм исследования функции на возрастание (убывание).

16.    Понятие максимума (минимума) функции. Алгоритм исследования функции на максимум (минимум).

17.    Общая схема исследования функции с помощью производной.

18.    Понятие функции двух переменных.

19.    Понятие частных производных.

20.    Понятие экстремума функции двух переменных. Алгоритм исследования функции двух переменных на экстремумы.

Для подготовки к самостоятельной работе:

1.        Прочитать учебник О₂: п. 7.1 – 7.14, 8.1 – 8.15, стр.90.

2.        Выучить лекцию.

3.        Подготовится к тестированию по пройденному материалу.

Скачано с www.znanio.ru