Лекции по дисциплине ЕН.01 Математика, СПО. Раздел 4. Интегральное исчисление и дифференциальные уравнения. Лекция № 7. Неопределённый интеграл

Раздел 4. Интегральное исчисление и дифференциальные уравнения.

Лекция № 7. Неопределённый интеграл. (4 часа)

План лекции:

1. Первообразная функция и неопределённый интеграл. (2 часа)

1.      Первообразная функция и неопределённый интеграл.

2.      Геометрический смысл неопределённого интеграла.

3.      Свойства неопределённого интеграла.

4.      Таблица основных неопределённых интегралов. (2 часа)

2. Основные правила неопределённого интегрирования.

1.      Метод замены переменной в неопределённом интеграле.

2.      Интегрирование подведением под знак дифференциала.

3.      Метод интегрирования по частям.

4.      Интегрирование дробей.

5.      Интегрирование рациональных функций и метод неопределённых коэффициентов.

6.      Интегрирование некоторых иррациональных функций.

7.      Интегрирование тригонометрических функций.

Литература:

1.    Электронный ресурс. О_3: Кремер, Н. Ш. Высшая математика для экономистов в 3 ч. Часть 3: учебник и практикум для среднего профессионального образования / под редакцией Н. Ш. Кремера. — 5-е изд., перераб. И доп. — Москва: Издательство Юрайт, 2023. — 417 с. — (Профессиональное образование). — ISBN 978-5-534-10171-3. — Текст: электронный // ЭБС Юрайт [сайт]. — URL: https://urait.ru/bcode/442440, п. 10.1 – 10.14, стр.70.

Формируемые знания, компетенции:

ЛР 4. Проявляющий и демонстрирующий уважение к людям труда, осознающий ценность собственного труда. Стремящийся к формированию в сетевой среде личностно и профессионального конструктивного «цифрового следа».

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.

З₃.Алгоритмы выполнения работ в профессиональной и смежных областях;

З₄.Методы работы в профессиональной и смежных сферах.

Основные понятия:

Интегрирование - действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).

Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство F'(x)=f(x), то есть данная функция f(x) является производной от первообразной функции F(x).

Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись ∫ f(x)dx, где знак ∫ называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.

Неопределённый интеграл геометрически представлен семейством всех интегральных кривых, как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.

Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.

Подведение под знак дифференциала решает возникающую при интегрировании проблему, заключающуюся в том, что в подынтегральном выражении находится сложная функция, например, , ,  и т. п., а под знаком дифференциала d - просто икс. То есть, нет возможности сразу применить таблицу интегралов для нахождения такого интеграла. Цель подведения под знак дифференциала - получить простую функцию, которую можно интегрировать непосредственно, то есть по таблице интегралов.

Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:  Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u, а остальная часть относится ко второму множителю и обозначается через dv. Затем дифференцированием находится du и интегрированием – функция v. При этом за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv - такую часть подынтегрального выражения, которая легко интегрируется.

1. ПЕРВООБРАЗНАЯ ФУНКЦИЯ И НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ.

1.Первообразная функция и неопределённый интеграл

Интегрирование - действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F(x) называется первообразной для функции f(x).

Определение 1. Функция F(x) называется первообразной для функции f(x) на некотором промежутке X, если для всех значений x из этого промежутка выполняется равенство F'(x)=f(x), то есть данная функция f(x) является производной от первообразной функции F(x).

Например, функция F(x) = sinx является первообразной для функции f(x) = cosx на всей числовой прямой, так как при любом значении икса (sinx)' = (cosx).

Определение 2. Неопределённым интегралом функции f(x) называется совокупность всех её первообразных. При этом употребляется запись

∫ f(x)dx,

где знак ∫ называется знаком интеграла, функция f(x) – подынтегральной функцией, а f(x)dx – подынтегральным выражением.

Таким образом, если F(x) – какая-нибудь первообразная для f(x) , то

∫ f(x)dx = F(x) + C, где C - произвольная постоянная (константа).                                              (1)

Замечание. Иногда символом   обозначается не вся совокупность первообразных, а какая-либо одна из них.

Примеры «неберущихся» интегралов

Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция - "быть дверью". А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции "быть дверью", то есть её неопределённым интегралом, является функция "быть деревом + С", где С - константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции "сделана" из первообразной функции при помощи формулы, которую мы узнали, изучая производную.

Тогда таблица функций распространённых предметов и соответствующих им первообразных ("быть дверью" - "быть деревом", "быть ложкой" - "быть металлом" и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых "сделаны" эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых усилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее, подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.

Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C, а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C, например, так: 5x³+С. Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x³+4 или 5x³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.

Поставим задачу интегрирования: для данной функции f(x) найти такую функцию F(x), производная которой равна f(x).

Пример 1.Найти множество первообразных функции .

Решение. Для данной функции первообразной является функция

 так как

Функция F(x) называется первообразной для функции f(x), если производная F(x) равна f(x), или, что одно и то же, дифференциал F(x) равен f(x)dx, т.е.

или                                                                   (2)

Следовательно, функция - первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции: 

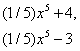
и вообще  где С – произвольная постоянная. В этом можно убедиться дифференцированием.

Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.

Теорема. Если F(x) – первообразная для функции f(x) на некотором промежутке Х, то любая другая первообразная для f(x) на том же промежутке может быть представлена в виде F(x) + C, где С – произвольная постоянная.

В следующем примере уже обращаемся к таблице интегралов, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полноте.

Пример 2. Найти множества первообразных функций:

1)           2)           3) .

Решение. Находим множества первообразных функций, из которых "сделаны" данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.

1) Применяя формулу (7) из таблицы интегралов при n = 3, получим

2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем

3) Так как

 то по формуле (7) при n = -1/4 найдём

Под знаком интеграла пишут не саму функцию f, а её произведение на дифференциал dx. Это делается, прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,

, ;

здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x, а во втором - как функция от z.

Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.

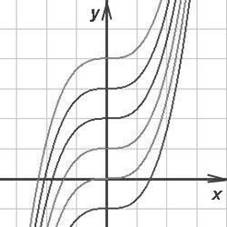
2.Геометрический смысл неопределённого интеграла

Пусть требуется найти кривую y=F(x) и мы уже знаем, что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.

Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F'(x). Значит, нужно найти такую функцию F(x), для которой F'(x)=f(x). Требуемая в задаче функция F(x)является первообразной от f(x). Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) - одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy.

Назовём график первообразной функции от f(x) интегральной кривой. Если F'(x)=f(x), то график функции y=F(x) есть интегральная кривая.

Неопределённый интеграл геометрически представлен семейством всех интегральных кривых, как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C.

3.Свойства неопределённого интеграла

Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.

Теорема 2. Неопределённый интеграл от дифференциала функции f(x) равен функции f(x) с точностью до постоянного слагаемого, т.е.

(3)

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.

Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

(4)

Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

(5)

4.Таблица основных неопределённых интегралов

Пользуясь таблицей неопределённых интегралов, свойствами неопределённого интеграла и методами интегрирования, можно отыскать неопределённый интеграл любой функции.

Из определения неопределённого интеграла вытекают следующие формулы, которые в дальнейшем будем называть табличными интегралами:

Закрепление изученного материала.

Пример 1. Найти неопределённый интеграл: .

Решение. Видим в знаменателе подынтегрального выражения многочлен, в котором икс в квадрате. Это почти верный признак того, что можно применить табличный интеграл (с арктангенсом в результате). Выносим из знаменателя множитель-двойку (есть такое свойство интеграла - постоянный множитель можно выносить за знак интеграла, выше оно было упомянуто как теорема 3). Результат всего этого:

.

Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:

.

Пример 2. Найти неопределённый интеграл: .

Решение. Вновь применяем теорему 3 - свойство интеграла, на основании которого постоянный множитель можно выносить за знак интеграла:

.

Применяем формулу из таблицы интегралов (переменная в степени) к подынтегральной функции:

.

Сокращаем получившиеся дроби и перед нами конечный ответ:

.

Пример 3. Найти неопределённый интеграл:

Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:

Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда

 где

объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования.

Пример 4. Найти неопределённый интеграл: .

Решение. Когда в знаменателе подынтегральной дроби - одночлен, можем почленно разделить числитель на знаменатель. Исходный интеграл превратился в сумму двух интегралов:

.

Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:

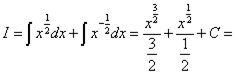
Пример 5. Найти неопределённый интеграл: .

Решение. Видим, что выражение подынтегральной функции содержит постоянный множитель 7, так как это выражение можно разделить на 7. Поэтому применяем правило, которое мы в теоретической части разобрали: выражение первообразной домножается на число, обратное постоянному множителю. Таким образом, выражение первообразной нужно домножить на 1/7. В свою очередь первообразная косинуса - это синус. Получаем:

.

Пример 6. Найти неопределённый интеграл: .

Решение. Видим, что выражение подынтегральной функции содержит постоянный множитель 2, так как это выражение можно разделить на 2. Поэтому применяем правило, которое мы в теоретической части разобрали: выражение первообразной домножается на число, обратное постоянному множителю. Таким образом, выражение первообразной нужно домножить на 1/2. В свою очередь первообразная синуса - это минус косинус. Получаем:

.

Вопросы для закрепления:

1. Понятие первообразной функции и неопределенного интеграла.

2. Таблица первообразных некоторых функций.

3. Основная задача интегрирования.

4. Геометрический смысл первообразной.

5. Свойства неопределенного интеграла.

6. Понятие криволинейной трапеции.

7. Вычисление площади криволинейной трапеции с помощью первообразных.

Для подготовки к самостоятельной работе:

1.        Прочитать учебник О₃: п. 10.1 – 10.2, стр.70.

2.        Выучить лекцию.

2. ОСНОВНЫЕ ПРАВИЛА НЕОПРЕДЕЛЁННОГО ИНТЕГРИРОВАНИЯ.

1. Метод замены переменной в неопределённом интеграле.

Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.

Вводится новая переменная, назовём её t. Например,

• в интеграле  можем ввести новую переменную ;
• в интеграле  можем ввести новую переменную ;
• в интеграле  можем ввести новую переменную .

Далее dx определяем как дифференциал по переменной t. После этого интеграл можно найти по таблице интегралов. Заменив обратно t на функцию от x, находим данный интеграл окончательно.

Прежде чем перейти к подробным решениям примеров, следует привести теорему, в которой обобщаются перечисленные выше действия.

Теорема. Пусть функция определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула

(1)

Формула (1) называется формулой замены переменной в неопределённом интеграле.

Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.

Пример 1. Найти неопределённый интеграл методом замены переменной:

Решение. Производим замену x – 1 = t; тогда x = t + 1. Отсюда dx = dt. По формуле (1)

Возвращаясь к переменной x, окончательно получаем

Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.

Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.

Пример 2. Найти неопределённый интеграл методом замены переменной: .

Решение. Положим . Отсюда

.              

По формуле (1)

Возвращаясь к переменной x, окончательно получаем

Пример 3. Найти неопределённый интеграл методом замены переменной: .

Решение. Положим , откуда  и .

Тогда , в свою очередь .

Заменяем переменную и получаем:

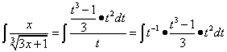, где степени при t складываются. Продолжаем преобразования и получаем:

Приводим дроби к общему знаменателю и возвращаемся к переменной x. Решаем и получаем ответ:

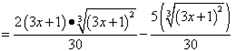
2.      Интегрирование подведением под знак дифференциала.

Подведение под знак дифференциала решает возникающую при интегрировании проблему, заключающуюся в том, что в подынтегральном выражении находится сложная функция, например, , ,  и т. п., а под знаком дифференциала d - просто икс. То есть, нет возможности сразу применить таблицу интегралов для нахождения такого интеграла.

Цель подведения под знак дифференциала - получить простую функцию, которую можно интегрировать непосредственно, то есть по таблице интегралов. Тогда путём преобразований подынтегрального выражения получим простую функцию переменной и эта переменная будет находится, и под знаком дифференциала d.

Решение заключается в том, что аргументом подынтегральной функции становится промежуточный аргумент ("внутренняя" функция исходной сложной функции, например, , ,  и т. п.), который можно обозначить буквой u, и тот же промежуточный аргумент u подводится под знак дифференциала d.

После того, как такой интеграл будет найден, на место буквы u возвращается обозначаемый ею промежуточный аргумент, и таким образом будет окончательно найден интеграл исходной сложной функции.

Формальная общая запись описанных преобразований выглядит так:

,

Где  - "внешняя" функция, а  - "внутренняя" функция или промежуточный аргумент.

В примерах вместо буквы u будем использовать букву t: так наши решения будут близки к наглядно понятному методу замены переменной. Кстати, в некоторых источниках метод подведения под знак дифференциала считается частным случаем метода замены переменной.

Пример 1. Найти подведением под знак дифференциала интеграл:.

Решение. Внесём под знак дифференциала внутреннюю функцию. Это почти то же самое, что найти её производную. Получаем: .

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя - тройки перед дифференциалом. Значит, перед знаком интеграла ставим 1/3 и получаем:

.

Далее для получения простой функции обозначаем  и  и окончательно решаем как табличный интеграл 7:

Пример 2. Найти подведением под знак дифференциала интеграл:.

Решение. Сразу же видим, что дифференциал синуса от икса равен косинусу от икса, а это как раз то, что нам нужно. Внесём под знак дифференциала синус от икса. Получаем

.

Полученное переносим в подынтегральное выражение: .

Далее для получения простой функции обозначаем  и  и окончательно решаем как табличный интеграл 7:

.

Пример 3. Найти подведением под знак дифференциала интеграл:.

Решение. Внесём под знак дифференциала внутреннюю функцию. Получаем

.

Полученное нужно перенести в подынтегральное выражение, но в нём нет множителя - двойки перед дифференциалом. Значит, перед знаком интеграла ставим 1/2 и получаем:

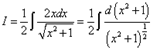
Далее для получения простой функции обозначаем  и  и окончательно решаем как табличный интеграл 7:

.

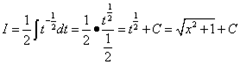3.      Метод интегрирования по частям.

Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:

Для применения формулы интегрирования по частям подынтегральное выражение нужно разбить на два множителя. Один из них обозначается через u, а остальная часть относится ко второму множителю и обозначается через dv. Затем дифференцированием находится du и интегрированием – функция v. При этом за u следует брать такую часть подынтегральной функции, которая при дифференцировании сильно не усложняется, а за dv - такую часть подынтегрального выражения, которая легко интегрируется.

Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит:

1)  - логарифмические функции, а также обратные тригонометрические функции (с приставкой "arc"), тогда на основании продолжительного опыта интегрирования по частям эти функции обозначаются через u;

2) , ,  - синус, косинус и экспоненту, умноженные на P(x) - произвольный многочлен от икса, тогда эти функции обозначают через dv, а многочлен - через u;

3) , , , , в этом случае интегрирование по частям применяется дважды.

Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную в самом начале занятия формулу интегрирования по частям

,

получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма. Интеграл алгебраической функции намного проще интеграла, под знаком которого находятся отдельно или вместе с алгебраическим множителем логарифмическая или обратная тригонометрическая функция.

Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.

Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:

Так как

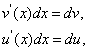  то её можно записать в виде

, который и был приведён в самом начале занятия.

При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С, равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.

Пример 1. Найти неопределённый интеграл методом интегрирования по частям:.

Решение. В подынтегральном выражении - логарифм, который, как мы уже знаем, разумно обозначить через u. Полагаем, что , .

Тогда , .

Находим (как уже говорилось в пояснении к теоретической справке, сразу же получаем в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма):

Пример 2. Найти неопределённый интеграл: .

Решение. Пусть , .

Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим
,  .

Применяя формулу интегрирования по частям, получаем:

Второй интеграл вновь находим по частям и получаем уже упомянутое преимущество (в первом слагаемом (без интеграла) логарифмическую функцию, а во втором слагаемом (под знаком интеграла) - функцию, не содержащую логарифма).

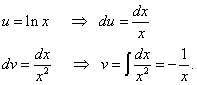
Находим изначальный интеграл:

Пример 3. Найти неопределённый интеграл методом интегрирования по частям:.

Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть , .

Тогда , .

Применяя формулу интегрирования по частям, получаем:

Второй интеграл находим методом замены переменной.

,   ,  

Возвращаясь к переменной x, получаем

.

Находим изначальный интеграл:

.

Пример 4. Найти неопределённый интеграл методом интегрирования по частям: .

Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что   находим 

4.      Интегрирование дробей.

Рациональной дробью называется дробь P(x)/Q(x), числитель P(x) и знаменатель Q(x) которой – многочлены. Рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе.

У любой неправильной дроби можно выделить её целую часть. Для этого следует по правилу деления многочленов разделить числитель на знаменатель. Поэтому любую неправильную дробь можно представить в виде суммы её целой части и некоторой правильной дроби.

Например, неправильную дробь

 можно представить в виде

Таким образом, если необходимо проинтегрировать неправильную дробь, то, представив её в виде суммы многочлена и правильной дроби, с помощью метода разложения сведём решение к интегрированию правильной дроби.

Ограничимся интегрированием лишь правильных рациональных дробей, знаменателями которых являются многочлены первой и второй степени. В общем виде интегралы от таких дробей записываются следующим образом:

(1)

(2)

При интегрировании дробей можно использовать следующую формулу, получаемую с помощью метода замены переменной:

(3)

Пример 1. Найти интеграл дроби

Подынтегральная функция является неправильной рациональной дробью. Используя приведённое выше её представление в виде суммы многочлена и правильной дроби, а также формулу (3), последовательно получим

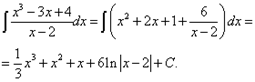
Любой интеграл вида (2) сводится к нахождению одного или двух следующих интегралов:

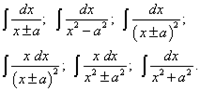(4)

Поэтому рассмотрим эти интегралы. Первый из них находится по формуле (3) при a = 1.

А теперь формулы для вычисления остальных приведённых интегралов.

(5)

(6)

(7)

(8)

(9)

Формулы (5)-(9) можно условно считать табличными интегралами. С их помощью можно найти любой интеграл вида (2). Предварительно такой интеграл приводят к интегралам группы (4). Для этого в знаменателе подынтегральной функции выделяют полный квадрат (это делается при помощи формул сокращённого умножения  и ) и представляют его в одном из следующих видов:

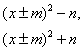
или   где m > 0 и n > 0.

В первых двух случаях замена переменной  в третьем непосредственное применение метода разложения приведёт к одному или двум интегралам группы (4).

Пример 2. Найти интеграл дроби

Решение. Результат применения формулы (5) при a = 8:

Пример 3. Найти интеграл дроби

Решение. Выделим в знаменателе подынтегральной функции полный квадрат:

а затем произведём замену переменной t = x + 3 (тогда dt = dx). В результате этого:

, то есть получили табличный интеграл. Применяем формулу 5):

, откуда, возвращаясь к старой переменной, окончательно получим

.

Пример 4. Найти интеграл дроби

Решение. Выделяя в знаменателе подынтегральной функции полный квадрат, получаем

Произведём теперь замену переменной t = x – 3 (или x = t + 3; тогда dx = dt). Поэтому

Результат применения формул (8) и (5) при a = 1:

Возвращаясь к "старой" переменной, окончательно получим

.

Пример 5. Найти интеграл дроби

Решение. Знаменатель представляет собой полный квадрат разности:

.

Поэтому .

Применяя далее формулы (7) и (6), найдём

5.      Интегрирование рациональных функций и метод неопределённых коэффициентов.

Рациональная функция - это дробь вида , числитель и знаменатель которой - многочлены или произведения многочленов.

Известно, что рациональные дроби бывают неправильные, если степень многочлена в её числителе не меньше степени многочлена в знаменателе, и правильные, если степень многочлена в числителе меньше степени многочлена в знаменателе. Необходимо представить неправильную дробь в виде суммы её целой части и некоторой правильной дроби.

Для интегрирования таких рациональных функции существует метод неопределённых коэффициентов, основанный на теореме, которая гласит, что всякая правильная дробь может быть представлена в виде суммы простых дробей.

Алгоритм интегрирования рациональных функций

·        Шаг 1. Определить вид многочлена в знаменателе дроби (он может иметь действительные, кратные действительные, комплексные и кратные комплексные корни) и в зависимости от вида разложить дробь на простые дроби, в числителях которых - неопределённые коэффициенты, число которых равно степени знаменателя.

·        Шаг 2. Определить значения неопределённых коэффициентов. Для этого потребуется решить систему уравнений, сводящуюся к системе линейных уравнений.

·        Шаг 3. Найти интеграл исходной рациональной функции (дроби) как сумму интегралов полученных простых дробей, к которым применяются табличные интегралы.

Шаг 1: разложение исходной дроби.

Многочлен в знаменателе имеет действительные корни. То есть, в знаменателе имеет место цепочка сомножителей вида , в которой каждый из сомножителей находится в первой степени. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

Пример 1. Шаг 1. Дан интеграл от рациональной функции .

От нас требуется разложить подынтегральное выражение - правильную дробь на простые дроби.

Решение. Дискриминант уравнения  положительный, поэтому многочлен в знаменателе имеет действительные корни. Получаем следующее разложение исходной дроби на сумму простых дробей:

.

Пример 2. Шаг 1.Дан интеграл от рациональной функции

.

Решение. Разложим знаменатель подынтегрального выражения на множители. Сначала можно вынести за скобки x. (На сайте есть урок о вынесении общего множителя за скобки.) Получаем следующую дробь:

.

Для разложения квадратного трёхчлена в скобках решаем квадратное уравнение:

Получаем разложение знаменателя на множители в подынтегральном выражении:

.

Дискриминант решённого выше квадратного уравнения положительный, то есть имеем дело со случаем, когда многочлен в знаменателе имеет действительные корни. Разложение исходной дроби подынтегрального выражения будет следующим:

.

Как и в первом примере, числа, обозначенные большими буквами, пока неизвестны. Отсюда и название - метод неопределённых коэффициентов.

Многочлен в знаменателе имеет кратные действительные корни. Этот случай имеет место, когда в цепочке сомножителей в знаменателе присутствует выражение вида , то есть один из многочленов в степени 2 и больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

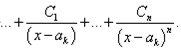
Пример 3. Шаг 1. Дан интеграл от рациональной функции .

Решение. Представляем разность квадратов  в виде произведения суммы и разности .

Тогда подынтегральное выражение запишется в виде

, все уравнения с многочленами которого имеют действительные корни. Это случай кратных действительных корней, так как последний сомножитель находится во второй степени. Получаем следующее разложение исходной дроби на простые дроби:

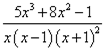
Как видим, в этом случае нужно понижать степень кратного многочлена с исходной до первой и записывать простую дробь с каждой из этих степеней в знаменатель.

Пример 4. Шаг 1. Дан интеграл от рациональной функции .

Решение. Уравнения с многочленами в знаменателе имеют действительные корни, а сами многочлены присутствуют в степенях больше первой. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Многочлен в знаменателе имеет комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля. В этом случае при разложении дроби в простой дроби, соответствующей описанному выше сомножителю, в числителе нужно записывать линейное выражение с переменной x (это выражение - последнее в следующей записи):

Пример 5. Шаг 1. Дан интеграл от рациональной функции .

Решение. Уравнение в скобках имеет комплексные корни, а оба сомножителя присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:

.

Пример 6. Шаг 1. Дан интеграл от рациональной функции .

Решение. Представим знаменатель дроби в подынтегральном выражении в виде следующего произведения сомножителей:

.

Решение. Уравнение с последним сомножителем имеет комплексные корни, а все сомножители присутствуют в знаменателе в первой степени. Поэтому получаем следующее разложение исходной дроби на простые дроби:

Многочлен в знаменателе имеет кратные комплексные корни: дискриминант квадратного уравнения , присутствующего в цепочке сомножителей в знаменателе, меньше нуля и этот сомножитель присутствует в степени 2 или больше. В этом случае разложение дроби с использованием метода неопределённых коэффициентов будет следующим:

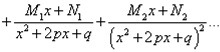
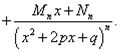
То есть в сумме простых дробей число простых дробей с линейным выражением в числителе должно быть равно степени сомножителя, имеющего комплексные корни.

Пример 7. Шаг 1. Дан интеграл от рациональной функции .

Решение. Квадратный трёхчлен  имеет комплексные корни и присутствует в знаменателе подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:

.

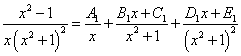Пример 8. Шаг 1. Дан интеграл от рациональной функции .

Решение. Квадратный трёхчлен в знаменателе имеет комплексные корни и присутствует в подынтегральной дроби во второй степени. Поэтому получаем следующее разложение дробного выражения:

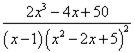
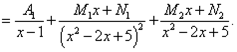
Шаг 2: нахождение неопределённых коэффициентов

На первом шаге мы представили подынтегральные дроби в виде суммы дробей с неопределёнными коэффициентами. В начале этого шага потребуется привести полученную сумму дробей к общему знаменателю. После этого в их числителях будут произведения неопределённых коэффициентов на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях.

Полученное таким образом выражение приравнивается к числителю исходной дроби. Затем составляется система из уравнений, в которых степени икса одинаковы. Путём решения системы и находятся неопределённые коэффициенты. Для решения достаточно знать, как системы уравнений решаются методом подстановки и методом сложения.

Пример 1. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Умножаем неопределённые коэффициенты на многочлены, которых нет в данной отдельной дроби, но которые есть в других полученных дробях:

.

Раскрываем скобки и приравниваем полученное к полученному выражению, числитель исходной подынтегральной дроби:

.

В обеих частях равенства отыскиваем слагаемые с одинаковыми степенями икса и составляем из них систему уравнений:

.

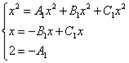Сокращаем все иксы и получаем эквивалентную систему уравнений:

.

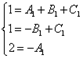Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Таким образом, окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 2. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Теперь начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Теперь требуется составить и решить систему уравнений. Для этого приравниваем коэффициенты при переменной в соответствующей степени в числителе исходного выражения функции и аналогичные коэффициенты в полученном на предыдущем шаге выражения:

Решаем полученную систему:

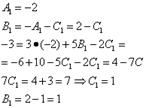
Итак, , отсюда получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 3. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Начинаем искать неопределённые коэффициенты. Для этого числитель исходной дроби в выражении функции приравниваем к числителю выражения, полученного после приведения суммы дробей к общему знаменателю:

Как и в предыдущих примерах составляем систему уравнений:

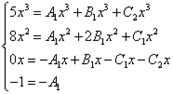
Сокращаем иксы и получаем эквивалентную систему уравнений:

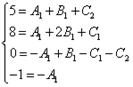
Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 4. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Как приравнивать числитель исходной дроби к выражению в числителе, полученному после разложения дроби на сумму простых дробей и приведения этой суммы к общему знаменателю, мы уже знаем из предыдуших примеров. Поэтому лишь для контроля приведём получившуюся систему уравнений:

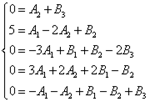
Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

Пример 5. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

Самостоятельно приводим к общему знаменателю эту сумму, приравнивать числитель этого выражения к числителю исходной дроби. В результате должна получиться следующая система уравнений:

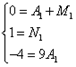
Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

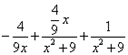Пример 6. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Производим с этой суммой те же действия, что и в предыдущих примерах. В результате должна получиться следующая система уравнений:

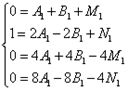
Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Пример 7. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

.

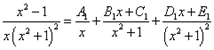После известных действий с полученной суммой должна получиться следующая система уравнений:

Решая систему, получаем следующие значения неопределённых коэффициентов:

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

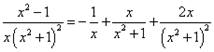Пример 8. Шаг 2. На шаге 1 получили следующее разложение исходной дроби на сумму простых дробей с неопределёнными коэффициентами в числителях:

Внесём некоторые изменения в уже доведённые до автоматизма действия для получения системы уравнений. Есть искусственный приём, который в некоторых случаях помогает избежать лишних вычислений. Приводя сумму дробей к общему знаменателю получаем и приравнивая числитель этого выражения к числителю исходной дроби, получаем:

Можно заметить, что если принять за значение икса единицу, то второе и третье слагаемые в правой части равенства обратятся в нули и нет необходимости их вычислять. Тогда получаем, что . Далее по уже отработанной схеме получаем систему уравнений:

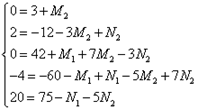
Решая систему, получаем следующие значения неопределённых коэффициентов:

.

Получаем окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Шаг 3: нахождение интеграла исходной функции (дроби)

Полученные простые дроби и интегрировать проще. К исходной сумме дробей применяется правило интеграла суммы (интеграл суммы равен сумме интегралов) и табличные интегралы. Чаще всего требуется применять табличные интегралы, приводящие к натуральному логарифму и арктангенсу.

Пример 1. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Интегрируем изначальную рациональную функцию как сумму дробей и используем табличный интеграл, приводящий к натуральному логарифму:

Последнее действие с натуральным логарифмом - приведение к единому выражению под логарифмом - может требоваться при выполнении работ, но требуется не всегда.

Пример 2. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Вновь применяем табличный интеграл, приводящий к натуральному логарифму:

Пример 3. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

.

В результате интегрирования получаем сумму натуральных логарифмов и одной простой дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:

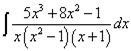
Пример 4. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

В результате интегрирования получаем сумму натуральных логарифмов и одной дроби, на случай, если требуется преобразование к единому логарифму, делаем и это:

Пример 5. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

.

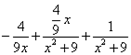Интегрируем и получаем сумму натурального логарифма и арктангенса:

Пример 6. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

.

Опять получаем сумму натурального логарифма и арктангенса:

Пример 7. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

.

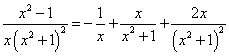Интегрируя, получаем натуральные логарифмы и дробь:

Приведение к единому логарифму попробуйте выполнить самостоятельно.

Пример 8. Шаг 3. На шаге 2 получили окончательное разложение подынтегральной дроби на сумму простых дробей:

.

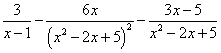Интегрируя, получаем сумму натурального логарифма, арктангенса и дроби:

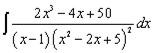
6.      Интегрирование некоторых иррациональных функций.

Рассмотрим интегралы от иррациональных функций, то есть функций, содержащих переменную (обычно икс) под корнем или, что то же самое - в дробной степени. Интегралы от таких функций с помощью подстановок приводятся к интегралам от рациональных функций и могут быть проинтегрированы окончательно.

В подынтегральном выражении - различные дробно-рациональные функции

Разберём интегралы, где в подынтегральном выражении переменная присутствует под корнем. В формально обобщённом виде речь идёт об интегралах вида

,

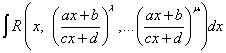где λ, ... μ - рациональные числа (целые или дробные).

В примерах мы увидим, что переменная икс, присутствующая под корнем, присутствует там без степени. В примере 3 икс присутствует также в квадрате, но при этом - не под корнем. То есть корни отдельно, степени - отдельно.

В этом случае важное значение имеет наименьшее общее кратное чисел λ, ... μ (или общий знаменатель, если эти числа дробные). Обозначим это наименьшее общее кратное (общий знаменатель) через n. Рассматриваемые интегралы от иррациональных функций можно найти, используя следующую подстановку:

Тогда каждая дробная степень "икса" выразится через целую степень "тэ" и подынтегральная функция преобразуется в рациональную функцию от "тэ".

Пример 1. Найти интеграл от иррациональной функции .

Решение. Преобразуем все корни икса в степени. Выписываем степени при иксе в подынтегральном выражении - все, которые там находим:

.

Находим наименьшее общее кратное знаменателей этих чисел: 4.

Поэтому используем следующую подстановку:

Подставляем и преобразуем:

Начинаем интегрировать:

Возвращаясь к переменной икс, окончательно находим:

.

Пример 2. Найти интеграл от иррациональной функции .

Решение. Используем следующую подстановку:

, ,  , 

Подставляем и преобразуем:

Интегрируем и получаем:

Возвращаясь к переменной икс, окончательно находим:

.

Корень из квадратного трёхчлена и подстановки Эйлера

Если дан интеграл иррациональной функции вида

,

то есть в подынтегральном выражении - корень из квадратного трёхчлена, то можно воспользоваться подстановками Эйлера.

Начинать нужно с разложения квадратного трёхчлена на множители:

, где x₁, x₂ - корни квадратного уравнения.

В зависимости от характера корней квадратного уравнения используются следующие подстановки Эйлера.

1. Если x₁, x₂ - действительные числа (не комплексные), то используется подстановка

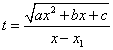 (первая подстановка Эйлера).

2. Если x₁, x₂ - комплексные числа и a > 0, то используется подстановка

(вторая подстановка Эйлера).

3. Если x₁, x₂ - комплексные числа и c > 0, то используется подстановка

(третья подстановка Эйлера).

Пример 5. Найти интеграл от иррациональной функции .

Решение. Разложим квадратный трёхчлен на множители:

Используем первую подстановку Эйлера:

,   ,  , 

,  

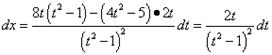
Подставляем:

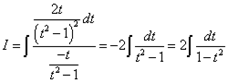
Интегрируем и получаем:

Возвращаясь к переменной икс, сначала долго занимаемся преобразованием выражений, а затем окончательно находим:

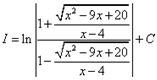
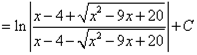
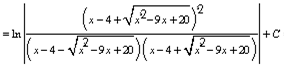
Пример 6. Найти интеграл от иррациональной функции .

Используем вторую подстановку Эйлера:

, , ,

, ,

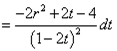Подставляем:

Интегрируем и получаем:

.

Возвращаясь к переменной икс, окончательно находим:

.

7.      Интегрирование тригонометрических функций.

Подынтегральное выражение можно преобразовать из произведения тригонометрических функций в сумму

Рассмотрим интегралы, в которых подынтегральная функция представляет собой произведение синусов и косинусов первой степени от икса, умноженного на разные множители, то есть интегралы вида

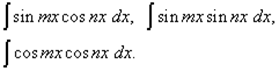(1)

Воспользовавшись известными тригонометрическими формулами

(2)
(3)
(4)
можно преобразовать каждое из произведений в интегралах вида (31) в алгебраическую сумму и проинтегрировать по формулам

(5)    и (6)
Пример 1. Найти интеграл от тригонометрической функции

Решение. По формуле (2) при

имеем

Поэтому

Применяя далее формулу (5), получим

Пример 2. Найти интеграл от тригонометрической функции .

Решение. По формуле (3) при  получаем следующее преобразование подынтегрального выражения:

Поэтому

Применяя далее формулу (6), получим

Пример 3. Найти интеграл от тригонометрической функции .

Решение. По формуле (4) при  получаем следующее преобразование подынтегрального выражения:

Применяя формулу (6), получим

Интеграл произведения степеней синуса и косинуса одного и того же аргумента

Рассмотрим теперь интегралы от функций, представляющих собой произведение степеней синуса и косинуса одного и того же аргумента, т.е.

(7)

В частных случаях один из показателей (m или n) может равняться нулю.

При интегрировании таких функций используется то, что чётную степень косинуса можно выразить через синус, а дифференциал синуса равен cosxdx (или чётную степень синуса можно выразить через косинус, а дифференциал косинуса равен - sinxdx).

Следует различать два случая: 1) хотя бы один из показателей m и n нечётный; 2) оба показателя чётные.

Пусть имеет место первый случай, а именно показатель n = 2k + 1 - нечётный. Тогда, учитывая, что  получим

Подынтегральное выражение представлено в таком виде, что одна его часть – функция только синуса, а другая – дифференциал синуса. Теперь с помощью замены переменной t = sinx решение сводится к интегрированию многочлена относительно t. Если же только степень m нечётна, то поступают аналогично, выделяя множитель sinx, выражая остальную часть подынтегральной функции через cosx и полагая t = cosx. Этот приём можно использовать и при интегрировании частного степеней синуса и косинуса, когда хотя бы один из показателей - нечётный. Всё дело в том, что частное степеней синуса и косинуса - это частный случай их произведения: когда тригонометрическая функция находится в знаменателе подынтегрального выражения, её степень - отрицательная. Но бывают и случаи частного тригонометрических функций, когда их степени - только чётные. О них - следующем абзаце.

Если же оба показателя m и n – чётные, то, используя тригонометрические формулы

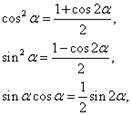
понижают показатели степени синуса и косинуса, после чего получится интеграл того же типа, что и выше. Поэтому интегрирование следует продолжать по той же схеме. Если же один из чётных показателей - отрицательный, то есть рассматривается частное чётных степеней синуса и косинуса, то данная схема не годится. Тогда используется замена переменной в зависимости от того, как можно преобразовать подынтегральное выражение. Такой случай будет рассмотрен в следующем параграфе.

Пример 4. Найти интеграл от тригонометрической функции .

Решение. Показатель степени косинуса – нечётный. Поэтому представим  в виде

и произведём замену переменной t = sinx (тогда dt = cosxdx). Тогда получим

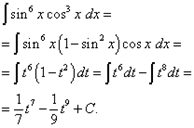
Возвращаясь к старой переменной, окончательно найдём

Пример 5. Найти интеграл от тригонометрической функции .

Решение. Показатель степени косинуса, как и в предыдущем примере – нечётный, но больше. Представим  в виде  и произведём замену переменной t = sinx (тогда dt = cosxdx). Тогда получим

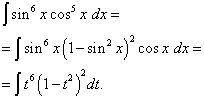
Раскроем скобки

 и получим

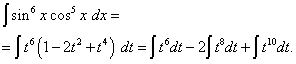
Возвращаясь к старой переменной, получаем решение

Пример 6. Найти интеграл от тригонометрической функции

Решение. Показатели степени синуса и косинуса – чётные. Поэтому преобразуем подынтегральную функцию так:

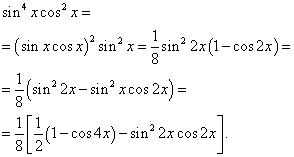
Тогда получим

Во втором интеграле произведём замену переменной, полагая t = sin2x. Тогда(1/2)dt = cos2xdx. Следовательно,

Окончательно получаем

Вопросы для закрепления:

1. Понятие первообразной функции и неопределенного интеграла.

2. Таблица первообразных некоторых функций.

3. Основная задача интегрирования.

4. Геометрический смысл первообразной.

5. Свойства неопределенного интеграла.

6. Понятие криволинейной трапеции.

7. Вычисление площади криволинейной трапеции с помощью первообразных.

8. Методы интегрирования.

Для подготовки к самостоятельной работе:

1.     Прочитать учебник О₃: п. 10.1 – 10.14, стр.70.

2.     Выучить лекцию.

Скачано с www.znanio.ru