BIR NOMA’LUMLI CHIZIQSIZ TENGLAMALARNI TAQRIBIY YECHISH.

MA’RUZA 2. BIR NOMA’LUMLI CHIZIQSIZ TENGLAMALARNI TAQRIBIY  YECHISH.

Reja :

1.     Algebraik va transstendent tenglamalarni taqribiy yechish usullari.

2.     Algebraik tenglama ildizlarini chegarasini aniqlash, ildizlarini ajratish.

3.     Oddiy iterasiya usuli.

4.     Nyuton usuli.

Teorema 1. Algebraik

                          (1)

tenglamaning barcha koeffisientlari haqiqiy va  bo’lsin. U holda (1) tenglamaning barcha ildizlari

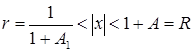
xalqa ichida yotadi. Bu yerda

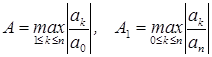.                                (2)

         Shuni eslatish lozimki, (1) tenglamaning barcha musbat ildizlari  oraliqda, barcha manfiy ildizlari esa  oraliqda yotadi. Lekin, ildizlarning chegarasi uchun bu baholar ancha qo’poldir. Quyidagi teoremalar bunga nisbatan yaxshiroq baholarni beradi.

         Lagranj teoremasi. Agar (1) tenglamaning manfiy koeffisientlaridan eng birinchisi (chapdan)  bo’lib,  manfiy koeffisientlarning absolyut qiymatlari bo’yicha eng kattasi bo’lsa, u holda musbat ildizlarning yuqori chegarasi

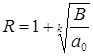                                               (3)

son bilan ifodalanadi.

         Nyuton teoremasi. Agar  uchun  ko’phad va uning ,  hosilalari nomanfiy, ya’ni , bo’lsa u holda  ni (1) tenglamaning musbat ildizlari uchun yuqori chegara deb olish mumkin.

         Quyidagi ko’phadlarni hosil qilaylik

,

,

.

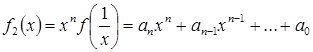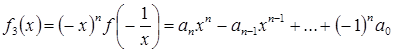           larning musbat ildizlarining yuqori chegaralarini mos ravishda  deb belgilaylik, u holda (1) tenglamaning barcha musbat ildizlari , hamma manfiy ildizlari 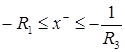 tengsizliklarni qanoatlantirishini ko’rish mumkin.

Misol.   tenglamaning haqiqiy ildizlari chegarasini toping.

         Yechish. Teorema 1 ga asosan . Demak, , ya’ni tenglamaning ildizlari  oraliqda joylashgan.

         Lagranj teoremasini qo’llasak,  Musbat ildizlar uchun yuqori chegara

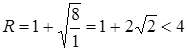
bo’ladi. Berilgan tenglamada  almashtirish qilsak  tenglama hosil bo’ladi. Bu tenglama musbat ildizlari uchun yuqori chegarani Lagranj teoremasiga ko’ra aniqlaymiz:  bo’lib,  ligi kelib chiqadi, ya’ni ildizlar (-4;4) oraliqda yotadi.

         Endi Nyuton teoremasini qo’llab ko’ramiz:

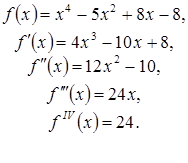
Bundan ko’rinib turibdiki,  uchun , demak,  musbat ildizlarning yuqori chegarasi ekan. Endi  tenglama uchun ildizlarning yuqori chegarasini topamiz

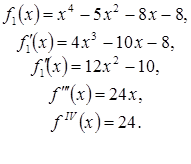
 shartlarda  uchun bajarilishini aniqlash qiyin emas. Demak, berilgan tenglamaning barcha haqiqiy ildizlari (-3;2) oraliqda yotar ekan.

Haqiqiy o’zgaruvchili uzluksiz f(x) funksiya berilgan bo’lsin.

                                           f(x)=0                                                         (1)

tenglamaning ildizlari yoki  y =f(x) funksiyaning nollarini topish talab qilingan bo’lsin. Algebraik ko’phadlar holida tenglamaning,  ildizlari kompleks bo’lishini bilamiz. Shuning uchun masalani yana іam aniqroq qo’yish lozim. (1) - tenglamaning kompleks tekislikning biror-bir sohasidagi ildizlarini toping degan masala qo’yish , yana іam aniqroq bo’ladi. Masalani yechish ikki bosqichdan iboratdir. Birinchi bosqichda ildizlarning joylashish sohasi aniqlanadi va ularni ajratishadi, ya’ni іar birida  birta ildizni o’z ichida saqlovchi sohalar aniqlanadi.Bundan tashqari yana karrali ildizlar va ularning karrali soni aniqlanadi. Shuning bilan birga ildizlarga biror-bir boshlang’ich yaqinlashishi topiladi. Ikkinchi bosqichda boshlang’ich berilganlardan foydalanib qidirilayotgan ildizni aniqlashtiruvchi  iterasion jarayon quriladi.

Ixtiyoriy tenglamaning ildizlari joylashgan sohani aniqlaydigan biror - bir yaxshi usul yo’q.

Algebraik tenglamalar  ildizlarining joylashishini aniqlovchi usullar ancha yaxshi o’rganilgan va bu usullarning bir qanchasi algebra kursidan sizga ma’lum.

Chiziqlimas tenglamalarni yechish usullari asosan iterasion bo’lib, ular qidirilayotgan yechimga (ildizga) yetarlicha yaqin bo’lgan boshlang’ich berilganning ma’lumligini (berilishini) talab qiladilar.

 Oddiy iterasiya usuli.

Bu usul (1)- tenglamani ekvivalent bo’lgan

                                                   x=S(x)                                                  (2)

tenglamaga almashtirilib iterasiyalar

                                          x_k+1=S(x_k), k=0,1,…                                    (3)

qoida bilan tashkil qilinadilar. Bunda x₀ boshlang’ich yaqinlashish beriladi. Iterasion ketma-ketlikning yaqinlashishi uchun S(x) funksiya katta rol o’ynaydi. Bu funksiyani turli usullar bilan aniqlash mumkin.

Odatda bu funksiya

                                          S(x)=x+t(x)f(x)                                           (4)

ko’rinishda aniqlanadi, bunda (x) ildiz qidirilayotgan sohada o’z ishorasini o’zgartirmaydigan funksiya. Bu usulning  bo’lganda yaqinlashishni keyinroq ko’rsatamiz. Xususiy іolda (x)==const bo’lganda

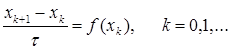                                  (5)

relaksasiya usuli deb aytiladi.

Optimal   parametrni  tanlash uchun relaksasiya tenglamasida

z_k = x_k - x_*

almashtnrish bajarib

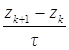=f(x_*+z_k)

xatolik tenglamasini hosil qilamiz.

O’rta qiymat haqidagi teoremaga asosan

(x_*+z_k) =(x_*) + z_k¢ (x_*+z_k) = z_k¢ (x_*+z_k)

tenglikka ega bo’lamiz. Bu yerda (0,1). Shunday qilib relaksasiya usulining xatoligi uchun

= ¢(x_*+z_k)z_k

tenglikka ega bo’lamiz.

Bundan

tengsizlik hosil bo’ladi.

Agar ildizning biror bir atrofida

                              (6)

munosabatlar bajarilsa

tengsizlikka ega bo’lamiz.

Shunday qilib optimal parametrni aniqlash

funksiyaning  bo’yicha minimumini topishga olib kelindi. q() funksiyaning grafigidan uning minimumi

shartdan aniqlanishi lozim ekanligi kelib chiqadi va

bo’ladi. - ning bu qiymatida

Shu sababli xatolik uchun

baho o’rinlidir.

Nyuton usuli.

Faraz qilamiz boshlang’ich yaqinlashish x₀ ma’lum bo’lsin.  f(x) funksiyani Teylor qatorining kesmasi bilan almashtiramiz.

(x)» H₁(x) = (x₀) + ¢(x₀)(x-x₀)

va keyingi yaqinlashish sifatida H₁(x) = 0  tenglama ildizini olamiz, ya’ni

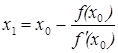
qilib olamiz.

Umuman, agar x_k yaqinlashish ma’lum bo’lsa, Nyuton usuli bo’yicha x_k+1   yaqinlashishi

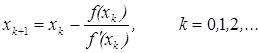                              (7)

kabi aniqlanadi.

Nyuton usuli, boshqacha yana urinmalar usuli іam deb aytiladi, chunki x_k+1 nuqta (x) funksiya grafigining (x_k,(x_k)) nuqtasida o’tkazilgan urinmaning abssissa  o’qi bilan kesishgan nuqtasining abssissa sidir. Bu usulning yaqinlashishi keyinroq ko’rsatiladi. Јozir bu usulning o’ziga xos xususiyatlarini bayon etamiz.

Birinchidan usul kvadratik yaqinlashishga ega, ya’ni keyingi qadamdagi yaqilashish xatoligi oldingi qadamdagi xatolikning kvadratiga proporsional:

x_k+1 - x_* = O((x_k - x_*)²).

Ikkinchidan usulning bunday yaqinlashishiga, boshlang’ich yaqinlashishning ildizga yetarlicha yaqin bo’lgandagina kafolat bersa bo’ladi. Agar boshlang’ich yaqinlashish noqulay tanlangan bo’lsa, usul yo sekin yaqinlashadi, yo umuman yaqinlashmasligi mumkin.

O’zgartirilgan Nyuton usuli.

Agar ¢(x) hosilaning qiymatini ko’p marta hisoblashdan qutilmoqchi bo’lsalar, unda

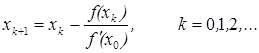
                             (8)

formuladan foydalanadilar.

Bu usul boshlang’ich yaqinlashishga uncha ko’p talab qo’ymaydi, lekin u sekin, faqat birinchi tartibli yaqinlashadi. (10) – usul   bo’lganda nolga bo’lish sodir bo’lmasligiga kafolat beradi.

Kesuvchilar  usuli

Bu usul Nyuton usulidan '(x_k) ni

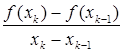
chekli ayirma bilan almashtirishdan hosil bo’ladi.

Natijada

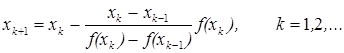                      (9)

ikki qadamli iterasion usul hosil bo’ladi. (9) - usulda oldin ikkita boshlang’ich x₀ , x₁  yaqinlashishlarni berishga to’g’ri  keladi. Bu usulning geometrik talqini quyidagidan iborat: (x_k-1,x_k) oraliqda y=(x) funksiya grafigi (x_k-1 , (x_k-1)) va (x_k, (x_k)) nuqtalardan o’tuvchi to’g’ri   chiziq bilan almashtirilib uning abssissa  o’qi bilan kesishgan nuqtasi keyingi yaqinlashish sifatida olinadi.

Oddiy iterasiya usulining yaqinlashishi.

 (x)=0                                                        (1)

tenglamani ekvivalent

x=(x)                                                       (2)

ko’rinishda yozamiz va x₀ dastlabki yaqinlashishni tanlab olib

x_k+1=(x_k),   k=0,1,…                                   (3)

oddiy iterasiyani qaraymiz. (3)-iterasiya yaqinlashadi deb aytiladi, agar {x_k} ketma-ketlik k®¥, limitga ega bo’lsa. µuyidagi teoremada (2)-tenglamaning yechimi mavjudligi va yagonaligiga kafolat beruvchi shartlar bayon qilinadi.

Agar  to’plamning ixtiyoriy x¢ , x¢¢  nuqtalari uchun

                                                   (4)

tengsizlik bajarilsa (x) funksiya  to’plamda Lipщist shartini qanoatlantiruvchi deb aytiladi (yoki lipщist uzluksiz) kelajakda x lar to’plami sifatida

Ur(a) =                                          (5)

markazi a- da bo’lgan uzunligi 2r ga teng kesma qaraladi.

Teorema. Agar (x) Ur(a) kesmada q(0,1) o’zgarmasli lipщist uzluksiz bo’lib,

                                          (6)

bajarilsa, unda (2)- tenglama Ur(a) da yagona x_*  yechimga ega bo’lib, (3)-iterasion ketma-ketlik ixtiyoriy x₀Ur(a) uchun x_* ga yaqinlashadi.

Xatolik uchun

                          (7)

(tengsizlik) baho o’rinli bo’ladi.

Isbot. Eng avval x_kU_r(a) k=1,2,.. ekanligini isbot qilamiz. Faraz qilamiz x_jUr(a) bo’lsin, x_j+1U_r(a) ekanligini isbot qilamiz.

tenglikdan

ekanligi ma’lum bo’ladi.

Bundan  lipщist - uzluksizlikni, indukstiya farazini va (6)- ni inobatga olib

ya’ni x_j+1U_r(a) ekanligini  hosil qilamiz.

Endi ikki qo’shni x_j+1  va x_j  yaqinlashishlar orasidagi farqni baholaymiz.

va barcha x_j  lar Ur(a) dan bo’lganligi uchun

yoki

                               (8)

tengsizlik hosil bo’ladi.

(8)- baho {x_k} ketma-ketlikni fundamental ekanligini ko’rsatishga imkon beradi. Јaqiqatdan іam  p  ixtiyoriy natural son bo’lsin.

Unda

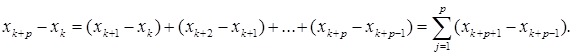
(8)- ga asosan

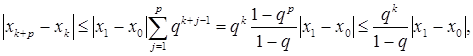
ya’ni

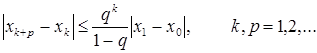                          (9)

bu tengsizlikdan  k®¥ , o’ng tomoni nolga intiladigan bo’lganligi uchun va p- ga bog’liq bo’lmaganligi uchun {x_k} ning fundamentalligi kelib chiqadi.

Demak

(3)- da limitga o’tib va (x) funksiyaning uzluksizligini hisobga olib

x_*=(x_*)

ekanligiga, ya’ni x_* ildiz ekanligiga ishonch hosil qilamiz. Faraz qilamiz x_*¢ (2)- ning Ur(a)- ga tegishli boshqa biror bir ildizi bo’lsin. Unda

|x_*-x_*'|=|(x_*)-(x_*')|

va teoremaning shartiga ko’ra

|x_*-x_*'|£ q|x_*-x_*'|.

Bunda q<1 bo’lganligi uchun, oxirgi tengsizlik  x_* = x_*' bo’lgandagina bajariladi, ya’ni yechim birdan-bir ekanligi kelib chiqadi.

(7)- tengsizlikni isbot qilamiz.

(3)- munosabatdan

x_k+1 - x_* = (x_k) - (x_*)

x_k  va x_*Ur(a)                           bo’lganligi uchun

|x_k+1-x_*|£ q|x_k-x_*|

hosil bo’ladi. Bu tengsizlik barcha  k=0,1,2,... uchun bajariladi.

Shuning uchun

1-Izoh. Agar biror bir iterasion usul uchun  bajarilsa, bunda qM₁  k-ga bog’liqmas bo’lsa, unda iterasion usul chiziqli q maxrajli geometrik progressiya tezligida yaqinlashadi deb aytiladi.

2-Izoh. (9) - da k- ni tanlab olib p- ni cheksizga intiltiramiz,

unda

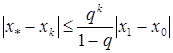
hosil bo’ladi. Bu tengsizlikning o’ng tomonida x₁ va x₀ yaqinlashishlar turadi, q-ma’lum son. Shu sababli bu tengsizlikdan iterasiya jarayonini to’xtatish uchun foydalanish qulaydir.

1-Natija:  Agar barchaxUr(a) uchun

                                                            (12)

bajarilib, (6) -shart o’rinli bo’lsa va x₀Ur(a) bo’lsa, (2)- tenglama birdan bir x_*Ur(a) yechimga ega, (3)- usul yaqinlashadi va (7)- baho o’rinlidir.

Јaqiqatdan іam ,(12)-dan

2- Natija.  Faraz qilamiz (2)- tenglama x_*- yechimga ega bo’lsin, S(x) funksiya

Ur(x_*) = {x : |x-x_*|£ r}                               (13)

kesmada uzluksiz differenstiallanuvchi va |'(x_*)|<1 bo’lsin. Unda shunday   > 0 mavjudki Ur(x_*) kesmada (2)- tenglama boshqa ildizga ega bo’lmaydi  va faqat x₀Ur(x_*) bo’lganda (3)- usul yaqinlashadi.

Nyuton usulining yaqinlashishi.

Oddiy іaqiqiy ildiz. Faraz qilamiz

f(x)=0                                                         (1)

tenglama oddiy іaqiqiy  x_*  ildizga ega bo’lsin,  f(x_*)=0  va  f'(x_*)¹ 0

bo’lsin. Faraz qilamiz f(x) funksiya x_* ildizning yetarlicha yaqin atrofida ikki marta uzluksiz hosilalarga ega bo’lsin.

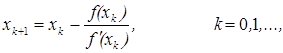
                          (2)

Nyuton usulini  tadqiq  etamiz. Eng avval (2)- ni oddiy iterasiya usulining xususiy іoli sifatida qaraymiz:

                                   (3)

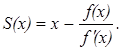                                               (4)

Oldin, biz (3)- usulning yaqinlashishi uchun ildizning yetarlicha yaqin atrofida

                                                     (5)

tengsizlikning bajarilishi etarli ekanligini ko’rsatgan edik.

(4)- funksiya uchun

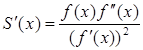
munosabat o’rinli.

Agar x_*,  f(x)  ning ildizi bo’lsa, unda ¢(x_*)=0 bo’ladi. Shu sababli ildizning shunday atrofi borki (5) - tengsizlik bajariladi. Demak x₀ boshlang’ich yaqinlashishni shunday tanlab olish mumkinki Nyuton usuli yaqinlashadi. Bu yaqinlashish oddiy yaqinlashish bo’lmasdan u aslida kvadratik yaqinlashishdir.

µuyidagi teorema Nyuton usulining kvadratik yaqinlashuvchi ekanligini ko’rsatadi.

1-teorema.  Faraz qilamiz x_* (1)-tenglamaning oddiy іaqiqiy ildizi bo’lib

Ur(x_*)={x : |x-x_*|<r}

atrofda  bo’lsin. Faraz qilamiz f¢¢(x) , Ur(x_*) atrofda uzluksiz  va

                           (6)

bo’lib ,

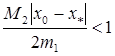
                                                 (7)

bo’lsin. Unda agar x₀Ur(x_*) bo’lsa, (2)- Nyuton usuli yaqinlashadi va xatolik uchun

                                          (8)

baho o’rinli , bunda

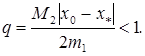
Скачано с www.znanio.ru