
Тема: Логарифмы и их свойства. Десятичные и натуральные логарифмы.
Логарифм числа
Остановимся на решении двух показательных уравнений.
Решение уравнения ![]() не вызывает труда. Так как 32=
не вызывает труда. Так как 32=![]() , то данное уравнение примет вид
, то данное уравнение примет вид ![]() . Поэтому уравнение имеет единственное решение x = 5.
. Поэтому уравнение имеет единственное решение x = 5.
А теперь рассмотрим уравнение ![]() . Обдумывая, ситуацию с таким показательным уравнением
математики ввели новый символ – логарифм. С помощью этого символа корень
уравнения
. Обдумывая, ситуацию с таким показательным уравнением
математики ввели новый символ – логарифм. С помощью этого символа корень
уравнения ![]() записали так:
записали так: ![]() (читается: логарифм числа 5 по основанию 2).
(читается: логарифм числа 5 по основанию 2).
В общем виде: ![]() ,
, ![]() .
.
|
Определение. Логарифмом положительного числа b по
основанию a ( |
Например:
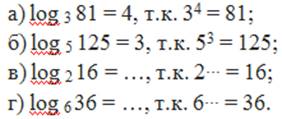
Основное логарифмическое тождество
Если корень ![]() подставить в уравнение
подставить в уравнение![]() , то получим формулу
, то получим формулу ![]() (b > 0, a > 0 и a ¹ 1), которая называется основным логарифмическим
тождеством.
(b > 0, a > 0 и a ¹ 1), которая называется основным логарифмическим
тождеством.
Это равенство является краткой символической записью определения логарифмов.
Операцию нахождения логарифма числа называют ЛОГАРИФМИРОВАНИЕМ.
· Решить примеры согласно тождеству:
![]()
Сравните.

Основные свойства логарифмов
Основные свойства логарифмов вытекают из определения логарифма и свойств показательной функции. При любом a > 0, a ≠ 1 и любых положительных x и y выполнены равенства:

Десятичные и натуральные логарифмы
На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10.
Логарифм положительного числа b по основанию 10 называют десятичным логарифмом числа b и обозначают lg b, т.е.
вместо ![]() пишут lg b.
пишут lg b.
Например,
![]()
Натуральным логарифмом
(обозначается ln) называется логарифм по
основанию e: ![]()
Примеры вычисления десятичных логарифмов
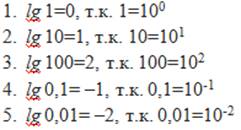

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.