Конспект урока по геометрии в 7 классе "Параллельные прямые"

Урок: Решение задач: «Параллельные прямые»

Цели:

·                    закрепление умений использовать знания признаков, свойств углов, образованных при пересечении параллельных прямых секущей;  научить видеть различные способы при решении одной задачи;

·                    продолжить формирование умений и навыков по решению задач; стимулировать учащихся к овладению решением задач;

·                    совершенствовать, развивать умения и навыки по решению задач на применение признаков и свойств параллельных прямых;

·                    развивать логическое мышление, учить анализировать и обобщать;

·                    продолжить работу по развитию математической речи и памяти;

·                    развитие логического мышления учащихся, внимания, активности, чувство ответственности, самостоятельности, культуры общения;

·                    продолжить формирование навыков эстетического оформления записей в тетради и выполнения чертежей;

·                    приучать к умению общаться и выслушивать других;

·                    развитие творческой самостоятельности и инициативы;

·                    воспитание познавательной активности, чувства ответственности, культуры общения.

Ход урока

I.  Организационный момент.

II. Актуализация знаний. Устно

1.  Расшифруйте анаграммы

·                    ослопктьс               (плоскость)

·                    ярмыеп                    (прямые)

·                    ен сепересяютка     (не пересекаются)

·                    лепаарльеын           (параллельные)

·                    ущексяа                   (секущая)

·                    рентвунтние            (внутренние)

·                    лоуг                          (угол)

Составить фразу по ключевым   словам.  Дайте определение всем известным понятиям.

2 . Закончи предложение

·                    Параллельными называются прямые…

·                    Перпендикулярными называются прямые, которые…

·                    Если прямые перпендикулярны третьей, то они между собой…

·                    Аксиома – это утверждение, которое….

·                    Теорема- это утверждение, справедливость которого…

3. Работа по рисунку:

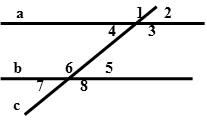
·                    Как называются углы, образованные двумя прямыми и секущей? Дайте им всем определение.

·                    Как называются эти углы: <4 и <5; <1 и <5; <4 и <6; <8 и <3; <1 и <6; <4 и <3; <7 и <5;    <3 и <5; <2 и <5?

4. Индивидуальная работа учащихся (3 учащихся на местах, 1 ученик - за доской выполняют задания одного варианта. Проверку осуществляют совместно всем классом)

 

 

III.  Решение задач

Решите задачи  по готовым чертежам у доски:

 

IV.  Физкульминутка

Рисуй глазами треугольник.

Теперь его переверни

Вершиной вниз.

И вновь глазами

ты по периметру веди.

Рисуй восьмерку вертикально.

Ты головою не крути,

А лишь глазами осторожно

Ты вдоль по линиям води.

И на бочок ее клади.

Теперь следи горизонтально,

И в центре ты остановись.

Зажмурься крепко, не ленись.

Глаза открываем мы, наконец.

Зарядка окончилась.

Ты – молодец!

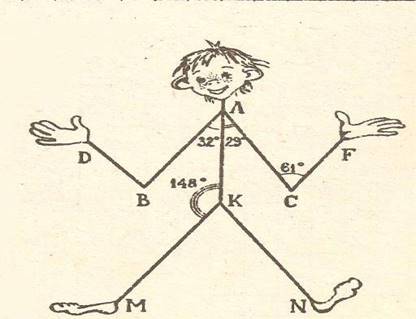
V. Решение занимательной задачи.

1. <ВАК=32,  <КАС=29,  <АСF=61,  <АКМ=148. Параллельны ли КМ  и СF?

 

 

VI. Диктант. (Учащиеся выполняют на листочках). Заполните пропуски в формулировке признаков, свойств углов при пересечении параллельных прямых секущей

1.      Две прямые на плоскости называются параллельными, если они…

2.      Если две параллельные прямые пересечены третьей, то сумма внутренних…

3.      Назовите на данном рисунке углы:

a.                 внутренние накрест лежащие… b.                соответственные… c.                 односторонние… d.                смежные (две пары)… e.                 вертикальные (две пары)…

4.                 Если один из внутренних накрест лежащих углов при параллельных прямых и секущей равен 34°

5.                 Если две параллельные прямые пересечены третьей, то соответственные…

6.                 Если один из односторонних углов при параллельных прямых и секущей равен 150°, то другой равен…

7.                 Будут ли прямые параллельными, если односторонние углы равны по 30° и 120°

                                                                Ответы к диктанту

 

VII.   Тест (выполняется в тетради)

1)Вычеркнуть лишние слова в скобках:

Аксиома – это (очевидные, принятые, исходные) положения геометрии, не требующие  (объяснений,  доказательств, обоснований).

Ответ: очевидно, принятые, объяснений, обоснований.

2) Выбрать окончание формулировки аксиомы параллельных прямых:

Через точку, не лежащую на данной прямой, проходит:

а) только одна прямая, параллельная данной;

б) всегда проходит прямая, параллельная данной;

в) только одна прямая, не пересекающаяся с данной.

Ответ: а.

3) Что может быть следствием аксиомы или теоремы? Указать неверные ответы.

а) Утверждение, не требующее доказательства.

б) Новая теорема, для доказательства которой использована аксиома или теорема.

в)  Утверждение, непосредственно выводимое из аксиомы или теоремы.

Ответ: а, б.

4) Указать следствия аксиомы параллельных прямых.

а) Если отрезок или луч пересекает одну из параллельных прямых, то он пересекает и другую.

б) Если две прямые параллельны третьей прямой, то они параллельны друг другу.

в) Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

г) Если три прямые параллельны, то любые две из них параллельны друг другу.

д) Если две прямые не параллельны третьей прямой, то они не параллельны между собой.

е)  Если прямая пересекает одну из параллельных прямых, то она не может пересекать другую.

ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой.

Ответ: б, в, е, ж.

5) Указать правильный ответ на вопрос.

Если через точку, лежащую вне прямой. Проведено несколько прямых, то сколько из них пересекаются с исходной прямой?

а) Неизвестно, так как не сказано, сколько прямых проведено через точку.

б) Все, кроме параллельной прямой.

в) Все, которые имеют на рисунке точку пересечения с исходной прямой.

Ответ: б.

6) Почему, если одна из прямых, проходящих через точку, лежащую вне заданной прямой, параллельна этой прямой, то другие прямые, проходящие через эту точку, не могут быть ей параллельны? Указать неправильный ответ на этот вопрос.

а) Это противоречит аксиоме параллельных прямых.

б) Любая другая пряма,. если она также параллельна заданной, совпадает с первой.

в) Все другие прямые имеют точку пересечения с заданной прямой, хотя она может находиться на сколь угодно большом расстоянии от исходной точки.

Ответ: в.

7. Сколько  углов образуется при пересечении двух параллельных прямых третьей?

1) 4.

2) 6.

3) 8.                                            Ответ: 3

4) 12.

8. Сколько равных острых углов может образоваться при пересечении двух параллельных прямых третьей?

1) 2.

2) 4. 

3) 6.                                              Ответ: 2.

4) 8.

9. Сколько равных тупых углов может образоваться при пересечении двух параллельных прямых третьей?

1) 2.

2) 4.

3) 8                                                Ответ: 2.

4) 16.

10. Сколько прямых углов может образоваться при пересечении двух параллельных прямых третьей?

1) 0

2) 2.

3) 4.                                                Ответ: 4

4) 8.

11. При пересечении двух параллельных прямых третьей один из углов оказался равным 34°. Найдите наименьший из всех образованных при этом углов.

1) Нельзя определить.

2) 34°.

3) 68°.                                              Ответ: 2.

4) 146°.

12. При пересечении двух параллельных прямых третьей один из углов оказался равным 112°. Найдите наименьший из всех образованных при этом углов.

1) Нельзя определить.

2) 34°.

3) 68°.                                               Ответ: 3.

4) 112°.

13. При пересечении двух параллельных прямых третьей один из углов оказался равным 97°. Найдите наименьший из всех образованных при этом углов.

1) 97°.

2) 83°.

3) 77°.                                             Ответ: 2.

4) 7°.

 

VIII. Итог урока. Рефлексия.

IX. Домашнее задание: ответить на вопросы для повторения; задание на выбор: составить кроссворд по теме "Параллельные прямые" (10-15 слов) или придумать 10-15 анаграмм или составить 5-8 ребусов.