КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВОРОНЕЖСКОЙ ОБЛАСТИ

«ШКОЛА № 1»

ФИЛИАЛ № 4

План-конспект открытого урока математики в 11 «А» классе

«Применение производной к исследованию функций»

Подготовил Федоров С.Н.,

учитель математики  1 КК

Борисоглебск, 2017

Открытый урок в 11 «А» классе

Тема: «Применение производной к исследованию функций»

Цель урока:

закрепление и систематизирование знаний обучающихся по исследованию функций с помощью производной;

развитие устной и письменной речи;

      воспитание нравственности и самостоятельности.

Оборудование: компьютер, доска, мультимедийный проектор, раздаточный материал.

Слайд 1. Тема урока.

  Тема нашего занятия – исследование функции и построение графиков с помощью производной.

Слайд 2. Цель урока

Цель урока – закрепить и систематизировать  знания обучающихся по исследованию функций с помощью производной.

Слайд 3.

1. Повторим, как определяются промежутки убывания и возрастания;

2.  Точки экстремума и значение функции в этих точках;

3.  наибольшее и наименьшее значение функции;

4.  Строится график функции

Слайд 4. Повторение теории.

Вопросы задаются поочерёдно каждой команде.

1) Какая функция называется возрастающей?

2) Какая функция называется убывающей?

3) Как связан “знак” производной с возрастанием и убыванием функции?

4) Что называется точкой максимума?

5) Что называется точкой минимума?

6) Какие точки называются стационарными?

7) Какие точки называются критическими?

8) Каков алгоритм нахождения наибольшего и наименьшего значений     непрерывной на заданном отрезке функции?

Слайд 5-6. «Найди ошибки» Каждой команде по 3 задания, команда решает, кто будет отвечать.

1. Изображён график производной.  Точки х=-1, х=1, х=2 являются точками максимума.

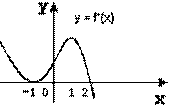
2. Производная функции в точке хо равна 0, значит хо - критическая точка. Верно ли?

3. Производная функции не существует в точке хо, значит хо - критическая точка. Верно ли?

4. Критическая точка является точкой экстремума. Верно ли?

5. Точка экстремума является критической точкой. Верно ли?

6. Функция y(x) непрерывна в точке x=4, причем y' (x)>0 на (1;4) и y'(x)<0 на (4;7). Точка x=4 является точкой минимума?

(см. Приложения)

Слайд 7.  «Бег с препятствиями», «Морской бой»

Повторим, как же нужно вычислять производные функций?

«Бег с препятствиями» - это эстафета, учащиеся идут поочерёдно к доске, на столе берут карточку с заданием, и выполняют его. Зарабатывают баллы по количеству верных заданий.

1 группа

2 группа

(см. Приложения)

Слайд 8. Из истории дифференциального исчисления

1.Он ввёл термин «производная» в 1797 г., что является буквальным переводом на русский язык французского слова deviree, он же ввел современные обозначения y¢, f¢. Такое название отражает смысл понятия: функция f¢(х) происходит из f(х), является производной от f(х).

2. Один из создателей (вместе с И. Ньютоном) дифференциального и интегрального исчислений В 1675 г показал взаимно-обратный характер дифференцирования и интегрирования. По просьбе Петра I разработал проекты развития образования и государственного управления в России. 

Кто эти учёные?

Слайд 9. Задание: Найти экстремумы функции.

 1 команде

1) y = x³ + 6x² - 15x - 3

2) y = 2х - x²

3) y = x/4 + 9/x

4) y = x/4 + 4/x

5) y = x – х⁴/4     

6) y = x³ - 6x² - 15x + 7

7) у = х³-6х²

2 команде

1) y = x³ + 6x² - 15x - 3

2) y = 2х - x²

3) y = x/4 + 9/x

4) y = x/4 + 4/x

5) y = 8x – х⁴/4

6) y = x³ - 6x² - 15x + 7

7) у = х³-6х²

Слайд 10.

                                              Жозеф Луи Лагранж

(1736-1813) французский математик и механик, иностранный почетный член Петербургской АН (1776).

Готфрид Вильгельм Лейбниц

(1646-1716), немецкий философ, математик, физик, языковед.

Слайд 11. Выполним лабораторную работу

З а д а н и я  1 команде: №1,№3     2 команде: №2, №4

  Для функции у = f(х) найдите:

1) область определения;

 2) производную;

3) критические точки;

4) промежутки монотонности и экстремумы.

 По результатам исследования постройте график.

Слайд 12

Слайд 13-14.

Первая  женщина математик С. В. Ковалевская сказала:

« Математик  должен быть поэтом в душе». И, следуя ее словам, мы на нашем уроке откроем литературную страничку «Графики функций – пословицы». Подберите к графикам функций, изображенных на слайдах, пословицы, которые раскрывают суть процессов функции:

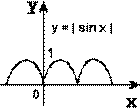
              1)

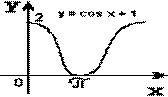
                 2)

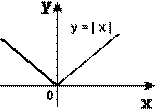
              3)

"Как аукнется, так и откликнется".

"Повторение - мать учения".

"Любишь с горы кататься, люби и саночки возить»

Слайд 15 Итоги игры (выставление оценок, выявление победителя в командном соревновании)

Слайд 16.  Домашнее задание (работа по карточкам)

Приложения

1 команде Задание: Найти экстремумы функции

1) y = x³ + 6x² - 15x - 3

2) y = 2х - x²

3) y = x/4 + 9/x

4) y = x/4 + 4/x

5) y = x – х⁴/4     

6) y = x³ - 6x² - 15x + 7

7) у = х³-6х²

2 команде Задание: Найти экстремумы функции

1) y = x³ + 6x² - 15x - 3

2) y = 2х - x²

3) y = x/4 + 9/x

4) y = x/4 + 4/x

5) y = 8x – х⁴/4

6) y = x³ - 6x² - 15x + 7

7) у = х³-6х²

1 команде Задание: Найти экстремумы функции

1) y = x³ + 6x² - 15x - 3

2) y = 2х - x²

3) y = x/4 + 9/x

4) y = x/4 + 4/x

5) y = x – х⁴/4     

6) y = x³ - 6x² - 15x + 7

7) у = х³-6х²

2 команде Задание: Найти экстремумы функции

1) y = x³ + 6x² - 15x - 3

2) y = 2х - x²

3) y = x/4 + 9/x

4) y = x/4 + 4/x

5) y = 8x – х⁴/4

6) y = x³ - 6x² - 15x + 7

7) у = х³-6х²

«Перестрелка» по таблице как игра в «Морской бой»

	1	2	3	4	5
А	Найти значение производной функции f(x) =  в точке х0= 2	Найти значение производной функции f(x) = 2 sin 3x  в точке х0= 0	Найти значение производной функции f(x) = +2  в точке х0= 1	Найти значение производной функции f(x) = sin x = cos x  в точке х0=p/2	Найти значение производной функции f(x) = cos x +2x  в точке х0= 0
Б	Определить монотонность функции и ее точки экстремумов, если f ,:  -         +       -            ·          ·    -9         -1	Определить монотонность функции и ее точки экстремумов, если f ,: +         -         -            ·          ·    -6          4	Определить монотонность функции и ее точки экстремумов, если f ,: +        -         +            ·          ·    -4           2	Определить монотонность функции и ее точки экстремумов, если f ,:  -         +       -            ·          ·     0           3	Определить монотонность функции и ее точки экстремумов, если f ,:  -     +      -     +        ·    ·      ·    -1     5      9
В	По графику производной определить монотонность функции:          -1  -2   ·          · -2	По графику производной определить монотонность функции:                 1        -1	По графику производной определить монотонность функции:                1                 2	По графику производной определить монотонность функции:             1     -1            1	По графику производной определить монотонность функции:                 1        2
Г	Найти производную функции: f(x) = x4-2x	Найти производную функции: f(x) = x8-x2+8	Найти производную функции: f(x) =2cos x2	Найти производную функции: f(x) =2cos2x	Найти производную функции: f(x) = cos(2x+3)
Д	По графику функции определить критические точки функции:           2 -2     -1	По графику функции определить критические точки функции:           3                   2	По графику функции определить критические точки функции:         4                2,5     -1           2    3      4	По графику функции определить критические точки функции:             2     -2        1         3       4	По графику функции определить критические точки функции:              1               1  2                              3

Скачано с www.znanio.ru