КОНТРОЛЬНАЯ РАБОТА № 8

Контрольная работа № 8

В а р и а н т  1

1. Решите неравенство:

а) x < 5;           б) 1 – 3х ≤ 0;           в) 5(у – 1,2) – 4,6 > 3у + 1.

2. При каких а значение дроби  меньше соответствующего значения дроби ?

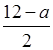3. Решите систему неравенств:

а) 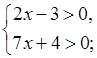           б)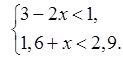

4. Найдите целые решения системы неравенств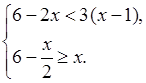

5. При каких значениях х имеет смысл выражение ?

6. При каких значениях а множеством решений неравенства 3x – 7 < является числовой промежуток (–∞; 4)?

В а р и а н т  2

1. Решите неравенство:

а) х ≥ 2;           б) 2 – 7х > 0;           в) 6(у – 1,5) – 3,4 > 4у – 2,4.

2. При каких b значение дроби  больше соответствующего значения дроби ?

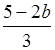3. Решите систему неравенств:

а) 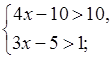           б)

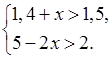
4. Найдите целые решения системы неравенств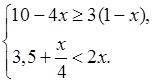

5. При каких значениях а имеет смысл выражение ?

6. При каких значениях b множеством решений неравенства 4х + 6 > является числовой промежуток (3; +∞)?

В а р и а н т  3

1. Решите неравенство:

а) х > 1;           б) 1 – 6х ≥ 0;           в) 5(у – 1,4) – 6 < 4у – 1,5.

2. При каких т значение дроби  меньше соответствующего значения выражения т – 6?

3. Решите систему неравенств:

а) 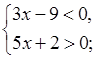           б)

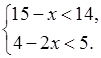
4. Найдите целые решения системы неравенств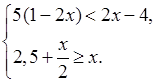

5. При каких значениях а имеет смысл выражение ?

6. При каких значениях а множеством решений неравенства 5х – 1 < является числовой промежуток (–∞; 2)?

В а р и а н т  4

1. Решите неравенство:

а) х ≤ 2;           б) 2 – 5х < 0;           в) 3(х – 1,5) – 4 < 4х + 1,5.

2. При каких а значение выражения а + 6 меньше соответствующего значения дроби ?

3. Решите систему неравенств:

а) 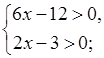           б)

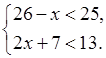
4. Найдите целые решения системы неравенств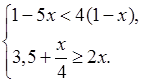

5. При каких значениях т имеет смысл выражение +
+?

6. При каких значениях b множеством решений неравенства 6х + 11 >
>  является числовой промежуток (1; +∞)?

Р е к о м е н д а ц и и   п о   о ц е н и в а н и ю.

Задания 1 и 3 соответствуют уровню обязательной подготовки. Для получения отметки «3» достаточно решить любые 2 задания. Для получения оценки «5» необходимо решить любые 5 заданий.

Решение вариантов контрольной работы

В а р и а н т  1

1. а) x < 5;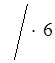

        х < 30;        (–∞; 30).

б) 1 – 3х ≤ 0;

    – 3х ≤ 1;

    х ≥ ;        .

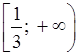в) 5(у – 1,2) – 4,6 > 3у + 1;

    5y – 6 – 4,6 > 3y + 1;

    5y – 3y > 1 + 6 + 4,6;

    2y > 11,6;

    y > 5,8;        (5,8; +∞).

О т в е т: а) (–∞; 30); б) 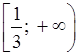; в) (5,8; +∞).

2. < ;

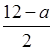
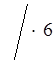    2(7 + a) < 3(12 – a);

    14 + 2a < 36 – 3a;

    2a + 3a < 36 – 14;

    5a < 22;

      a < 4,4.

О т в е т: при a < 4,4.

3. а)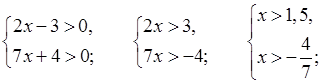

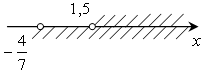         (1,5; +∞).

б)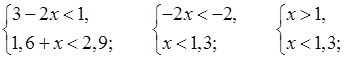

         (1; 1,3).

О т в е т: а) (1,5; +∞); б) (1; 1,3).

4.

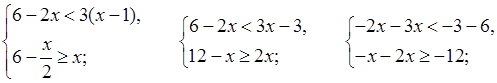
О т в е т: 2; 3; 4.

5. Выражение имеет смысл при х, удовлетворяющих системе:

 ≤ x ≤ 6.

О т в е т: при  ≤ x ≤ 6.

6. 3x – 7 <;

    9х – 21 < a;

    9x < a + 21;

    x < ;        .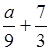

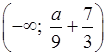Множеством решений является числовой промежуток (–∞; 4), если:

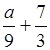 = 4;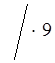

а + 21 = 36;

а = 15.

О т в е т: при а = 15.

В а р и а н т  2

1. а) х ≥ 2;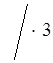

        х ≥ 6;        [6; +∞).

б) 2 – 7х > 0;

    –7x > –2;

    x < ;        .

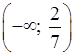в) 6(у – 1,5) – 3,4 > 4у – 2,4;

    6y – 9 – 3,4 > 4y – 2,4;

    6y – 4y > 9 + 3,4 – 2,4;

    2y > 10;

    y > 5;        (5; +∞).

О т в е т: а) [6; +∞); б) 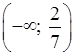; в) (5; +∞).

2.  > ;

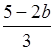
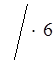    3(b + 4) >2(5 – 2b);

    3b + 12 > 10 – 4b;

    3b + 4b > 10 – 12;

    7b > –2;

    b > .

О т в е т: при b > .

3. а)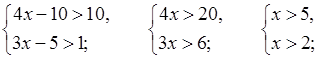

         (5; +∞).

б)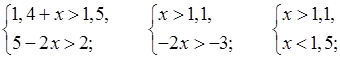

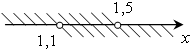         (1,1; 1,5).

О т в е т: а) (5; +∞); б) (1,1; 1,5).

4.

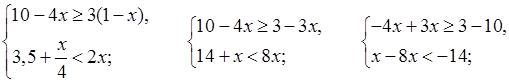
О т в е т: 3; 4; 5; 6; 7.

5. Выражение имеет смысл при х, удовлетворяющих системе:

–8 ≤ а ≤ 5.

О т в е т: при –8 ≤ а ≤ 5.

6. 4х + 6 >;

    20x + 30 > b;

    20x > b – 30;

    x > ;         .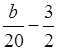

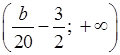Множеством решений является числовой промежуток (3; +∞), если:

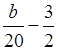 = 3;

b – 30 = 60;

b = 90.

О т в е т: при b = 90.

В а р и а н т  3

1. а) х > 1;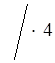

        х > 4;         (4; +∞).

б) 1 – 6х ≥ 0;

    – 6х ≥ –1;

    х ≤ ;         .

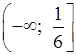в) 5(у – 1,4) – 6 < 4у – 1,5;

    5y – 7 – 6 < 4y – 1,5;

    5y – 4y < 7 + 6 – 1,5;

    y < 11,5;         (–∞; 11,5).

О т в е т: а) (4; +∞); б) 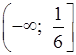; в) (–∞; 11,5).

2.  < т – 6;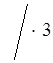

    m + 1 < 3(m – 6);

    m + 1 < 3m – 18;

    m – 3m < –1 – 18;

    –2т < –19;

    т > 9,5.

О т в е т: при т > 9,5.

3. а)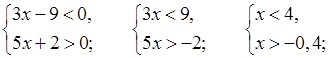

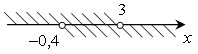         (–0,4; 3).

б)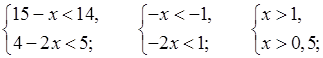

         (1; +∞).

О т в е т: а) (–0,4; 3); б) (1; +∞).

4.

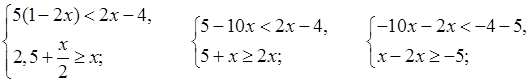
О т в е т: 1; 2; 3; 4; 5.

5. Выражение имеет смысл при a, удовлетворяющих системе:

–2 ≤ а ≤ 4.

О т в е т: при –2 ≤ а ≤ 4.

6. 5х – 1 <;

    20x – 4 < a;

    20x < a + 4;

    x < ;         .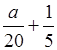

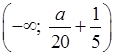Множеством решений является числовой промежуток (–∞; 2), если:

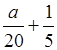 = 2;

а + 4 = 40;

а = 36.

О т в е т: при а = 36.

В а р и а н т  4

1. а) х ≤ 2;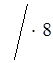

         х  16;         (–∞; 16].

б) 2 – 5х < 0;

    –5х < –2;

    х > 0,4;         (0,4; +∞).

в) 3(х – 1,5) – 4 < 4х + 1,5;

    3x – 4,5 – 4 < 4x + 1,5;

    3x – 4x < 4,5 + 4 + 1,5;

    –x < 10;

    х > –10;         (–10; +∞).

О т в е т: а) (–∞; 16]; б) (0,4; +∞); в) (–10; +∞).

2. а + 6 < ;

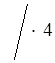    4(а + 6) < а + 2;

    4а + 24 < а + 2;

    4а – а < 2 – 24;

    3а < –22;

    а < –7.

О т в е т: при а < –7.

3. а)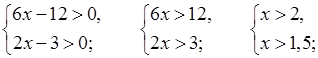

         (2; +∞).

б)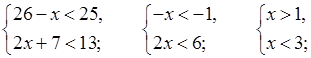

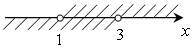         (1; 3).

О т в е т: а) (2; +∞); б) (1; 3).

4.

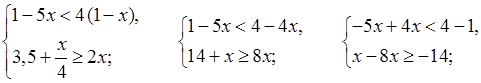
О т в е т: –2; –1; 0; 1; 2.

5. Выражение имеет смысл при m, удовлетворяющих системе:

–4 ≤ т ≤ 3.

О т в е т: при –4 ≤ т ≤ 3.

6. 6х + 11 >;

    24х + 44 > b;

    24x > b – 44;

    x > ;         .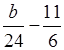

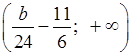Множеством решений является числовой промежуток (1; +∞), если:

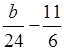 = 1;

b – 44 = 24;

b = 68.

О т в е т: при b = 68.