КОНТРОЛЬНАЯ РАБОТА № 8

Контрольная работа № 8

Вариант 1

1. Упростите выражение.

а) (x – 3) (x – 7) – 2x (3x – 5);                     в) 2 (m + 1)² – 4m.

б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители.

а) х³ – 9х;                                                          б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители.

а) 16х⁴ – 81;                                                     б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

Вариант 2

1. Упростите выражение.

а) 2х (х – 3) – 3х (х + 5);                                в) 3 (y + 5)² – 3y².

б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.

а) с³ – 16с;                                                        б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители.

а) 81а⁴ – 1;                                                       б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

Вариант 3

1. Упростите выражение.

а) 2c (1 + c) – (c – 2) (c + 4);             в) 30х + 3 (х – 5)².

б) (y + 2)² – 2y (y + 2);

2. Разложите на множители.

а) 4а – а³;                                                         б) ax² + 2ax + a.

3. Упростите выражение

4. Разложите на множители.

а) 16 – y⁴;                                                    б) a + a² – b – b².

5. Докажите, что выражение c² – 2c + 12 может принимать лишь положительные значения.

Вариант 4

1. Упростите выражение

а) 5a (2 – a) + 6a (a – 7);                              в) 20x + 5 (x – 2)².

б) (b – 3) (b – 4) – (b + 4)²;

2. Разложите на множители.

а) 25у – у³;                                                        б) –4x² + 8xу – 4у².

3. Упростите выражение

4. Разложите на множители.

а)  – b⁴;                                                        б) a² – x² + 4x – 4.

5. Докажите, что выражение –у² + 2у – 5 при любых значениях у принимает отрицательные значения.

Решение заданий контрольной работы

Вариант 1

1. а)
= –5x² + 21;

    б)

    в)
= 2m² + 2.

2. а) х³ – 9х = х (х² – 9) = х (х – 3) (х + 3);

    б)

3.

4. а) 16х⁴ – 81 =
× (4x² + 9);

    б)
= (x + y) (x – y – 1).

5. Выделим из данного трёхчлена квадрат двучлена:

Выражение (х – 2)² не может быть отрицательным ни при каких значениях х. Значит, выражение (х – 2)² + 5 принимает положительные значения при любых х.

Вариант 2

1. а)

    б)

    в) 75 – 3y² =
= 30y + 75.

2. а) с³ – 16с = с (с² – 16) = с (с – 4) (с + 4);

    б)

3.

4. а) 81а⁴ – 1 =

    б)
= (y – (x + 3)) (y + (x + 3)) = (y – x – 3) (y + x + 3).

5. Выделим из данного трёхчлена квадрат двучлена:

Выражение –(а – 2)² не может принимать положительных значений ни при каком значении а. Значит, выражение –(а – 2)² – 5 может принимать только отрицательные значения.

Вариант 3

1. а)

    б)

    в) 30x + 75 =
= 3x² + 75.

2. а) 4а – а³ = а (4 – а²) = а (2 – а) (2 + а);

    б)

3.

4. а)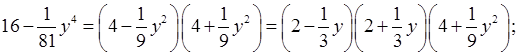

    б)
= (a – b) (a + b + 1).

5. Выделим из данного трёхчлена квадрат двучлена:

Выражение (с – 1)² не может принимать отрицательных значений ни при каком значении с. Значит, выражение (с – 1)² + 11 может принимать только положительные значения.

Вариант 4

1. а)

    б)
= –15b – 4;

    в) 20 =
= 5x² + 20.

2. а) 25у – у³ = у (25 – у²) = у (5 – у) (5 + у);

   б)

3.

4. а)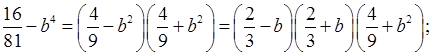

    б)
= (a – (x – 2)) (a + (x – 2)) = (a – x + 2) (a + x – 2).

5. Выделим из данного трёхчлена квадрат двучлена:

Выражение –(у – 1)² не может принимать положительных значений ни при каком значении у. Значит, выражение –(у – 1)² – 4 может принимать только отрицательные значения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5);                       в) 2 (m + 1)² – 4m.    б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители.  а) х³ – 9х;                                                                    б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81;                                                                б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y².    б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.      а) с³ – 16с;                                                                             б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;                                                                  б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5);                       в) 2 (m + 1)² – 4m.    б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители.  а) х³ – 9х;                                                                    б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81;                                                                б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y².    б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.      а) с³ – 16с;                                                                             б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;                                                                  б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5);                       в) 2 (m + 1)² – 4m.    б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители.  а) х³ – 9х;                                                                    б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81;                                                                б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y².    б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.      а) с³ – 16с;                                                                             б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;                                                                  б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5);                       в) 2 (m + 1)² – 4m.    б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители.  а) х³ – 9х;                                                                    б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81;                                                                б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

 

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y².    б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.      а) с³ – 16с;                                                                             б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;                                                                  б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

 

Вариант 1

1. Разложите на множители.

а) 3х² – 12;                                 в) ax² + 4ax + 4a;

б) –3a³ + 3ab²;                                         г) –3x² + 12x – 12.

2. Представьте в виде произведения.

а)                       б)

3*. Какой многочлен надо записать вместо *, чтобы получившееся равенство было тождеством:

(x + 1) ∙  * = x² + 3x + 2?

 

Вариант 2

1. Разложите на множители.

а) 5x² – 45;                                 в) ax² – 2axy + ay²;

б) –2ay² + 2a³;                                          г) –2x² – 8x – 8.

2. Представьте в виде произведения.

а)                      б)

3*. Какой многочлен надо записать вместо *, чтобы получившееся равенство было тождеством:

(x – 1) ∙  * = x² – 4x + 3?

 

Вариант 1

1. Разложите на множители.

а) 3х² – 12;                                 в) ax² + 4ax + 4a;

б) –3a³ + 3ab²;                                         г) –3x² + 12x – 12.

2. Представьте в виде произведения.

а)                       б)

3*. Какой многочлен надо записать вместо *, чтобы получившееся равенство было тождеством:

(x + 1) ∙  * = x² + 3x + 2?

 

Вариант 2

1. Разложите на множители.

а) 5x² – 45;                                 в) ax² – 2axy + ay²;

б) –2ay² + 2a³;                                          г) –2x² – 8x – 8.

2. Представьте в виде произведения.

а)                      б)

3*. Какой многочлен надо записать вместо *, чтобы получившееся равенство было тождеством:

(x – 1) ∙  * = x² – 4x + 3?

 

Вариант 2

1. Разложите на множители.

а) 5x² – 45;                                 в) ax² – 2axy + ay²;

б) –2ay² + 2a³;                                          г) –2x² – 8x – 8.

2. Представьте в виде произведения.

а)                      б)

3*. Какой многочлен надо записать вместо *, чтобы получившееся равенство было тождеством:

(x – 1) ∙  * = x² – 4x + 3?

 

 

 

 

 

Вариант 3

1. Упростите выражение.

а) 2c (1 + c) – (c – 2) (c + 4);                в) 30х + 3 (х – 5)².  б) (y + 2)² – 2y (y + 2);

2. Разложите на множители.  а) 4а – а³;                                                                   б) ax² + 2ax + a.

3. Упростите выражение

4. Разложите на множители.а) 16 – y⁴;                                                                б) a + a² – b – b².

5. Докажите, что выражение c² – 2c + 12 может принимать лишь положительные значения.

 

Вариант 4

1. Упростите выражениеа) 5a (2 – a) + 6a (a – 7);  в) 20x + 5 (x – 2)².   б) (b – 3) (b – 4) – (b + 4)²;

2. Разложите на множители.а) 25у – у³;                                                                    б) –4x² + 8xу – 4у².

3. Упростите выражение

4. Разложите на множители.а)  – b⁴;                                                                     б) a² – x² + 4x – 4.

5. Докажите, что выражение –у² + 2у – 5 при любых значениях у принимает отрицательные значения.

 

 

Вариант 3

1. Упростите выражение.

а) 2c (1 + c) – (c – 2) (c + 4);                в) 30х + 3 (х – 5)².  б) (y + 2)² – 2y (y + 2);

2. Разложите на множители.  а) 4а – а³;                                                                   б) ax² + 2ax + a.

3. Упростите выражение

4. Разложите на множители.а) 16 – y⁴;                                                                б) a + a² – b – b².

5. Докажите, что выражение c² – 2c + 12 может принимать лишь положительные значения.

 

Вариант 4

1. Упростите выражениеа) 5a (2 – a) + 6a (a – 7);  в) 20x + 5 (x – 2)².   б) (b – 3) (b – 4) – (b + 4)²;

2. Разложите на множители.а) 25у – у³;                                                                    б) –4x² + 8xу – 4у².

3. Упростите выражение

4. Разложите на множители.а)  – b⁴;                                                                     б) a² – x² + 4x – 4.

5. Докажите, что выражение –у² + 2у – 5 при любых значениях у принимает отрицательные значения.

 

Вариант 3

1. Упростите выражение.

а) 2c (1 + c) – (c – 2) (c + 4);                в) 30х + 3 (х – 5)².  б) (y + 2)² – 2y (y + 2);

2. Разложите на множители.  а) 4а – а³;                                                                   б) ax² + 2ax + a.

3. Упростите выражение

4. Разложите на множители.а) 16 – y⁴;                                                                б) a + a² – b – b².

5. Докажите, что выражение c² – 2c + 12 может принимать лишь положительные значения.

 

Вариант 4

1. Упростите выражениеа) 5a (2 – a) + 6a (a – 7);  в) 20x + 5 (x – 2)².   б) (b – 3) (b – 4) – (b + 4)²;

2. Разложите на множители.а) 25у – у³;                                                                    б) –4x² + 8xу – 4у².

3. Упростите выражение

4. Разложите на множители.а)  – b⁴;                                                                     б) a² – x² + 4x – 4.

5. Докажите, что выражение –у² + 2у – 5 при любых значениях у принимает отрицательные значения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5); в) 2 (m + 1)² – 4m  б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители  а) х³ – 9х;   б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81; б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y²   б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.  а) с³ – 16с;   б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;   б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5); в) 2 (m + 1)² – 4m  б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители  а) х³ – 9х;   б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81; б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y²   б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.  а) с³ – 16с;   б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;   б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5); в) 2 (m + 1)² – 4m  б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители  а) х³ – 9х;   б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81; б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y²   б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.  а) с³ – 16с;   б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;   б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

Вариант 1

1. Упростите выражение. а) (x – 3) (x – 7) – 2x (3x – 5); в) 2 (m + 1)² – 4m  б) 4a (a – 2) – (a – 4)²;

2. Разложите на множители  а) х³ – 9х;   б) –5a² – 10ab – 5b².

3. Упростите выражение

4. Разложите на множители. а) 16х⁴ – 81; б) х² – х – y² – y.

5. Докажите, что выражение х² – 4х + 9 при любых значениях х принимает положительные значения.

 

 

 

Вариант 2

1. Упростите выражение. а) 2х (х – 3) – 3х (х + 5);  в) 3 (y + 5)² – 3y²   б) (a + 7) (a – 1) + (a – 3)²;

2. Разложите на множители.  а) с³ – 16с;   б) 3a² – 6ab + 3b².

3. Упростите выражение

4. Разложите на множители. а) 81а⁴ – 1;   б) y² – х² – 6х – 9.

5. Докажите, что выражение –а² + 4а – 9 может принимать лишь отрицательные значения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Упростите выражение.

а) 2c (1 + c) – (c – 2) (c + 4);          б) 30х + 3 (х – 5)²              в ) (y + 2)² – 2y (y + 2);

 г) 5a (2 – a) + 6a (a – 7);       д) 20x + 5 (x – 2)²            е) (b – 3) (b – 4) – (b + 4)²;

2. Разложите на множители.

а) 4а – а³;                      б) ax² + 2ax + a.

в) 25у – у³;                    г) –4x² + 8xу – 4у².

3. Упростите выражение

а)    б)

4. Разложите на множители.

а) 16 – y⁴;        б) a + a² – b – b².         в)  – b⁴;                 г) a² – x² + 4x – 4.

 

5. Докажите, что выражение

а) c² – 2c + 12 может принимать лишь положительные значения.

б) –у² + 2у – 5 при любых значениях у принимает отрицательные значения.

 

 

 

1. Упростите выражение.

а) 2c (1 + c) – (c – 2) (c + 4);          б) 30х + 3 (х – 5)²              в ) (y + 2)² – 2y (y + 2);

 г) 5a (2 – a) + 6a (a – 7);       д) 20x + 5 (x – 2)²            е) (b – 3) (b – 4) – (b + 4)²;

2. Разложите на множители.

а) 4а – а³;                      б) ax² + 2ax + a.

в) 25у – у³;                    г) –4x² + 8xу – 4у².

3. Упростите выражение

а)    б)

4. Разложите на множители.

а) 16 – y⁴;        б) a + a² – b – b².         в)  – b⁴;                 г) a² – x² + 4x – 4.

 

5. Докажите, что выражение

а) c² – 2c + 12 может принимать лишь положительные значения.

б) –у² + 2у – 5 при любых значениях у принимает отрицательные значения.