Контрольная работа за 1 полугодие в 11 кл.

А) y =            Б)  y = 5;         В)  y = sin x;         Г) y =.

2. Запишите уравнение касательной к графику функции

y = 3x 2 - 2x -1   в  его точке с абсциссой, равной 1.

3. Если значения производной во всех точках промежутка отрицательны, то функция на этом промежутке:

                    а)  возрастает;                               в)  не изменяется;

                    б)  убывает;                                    г)  другой ответ.

4. Если производная функции при переходе через точку х0 меняет знак с минуса на плюс, то в этой точке данная функция:

                    а)  имеет максимум;                     в)  возрастает;

                    б)  имеет минимум;                       г)   другой ответ.

5. Тело движется по прямой так, что расстояние s до него от некоторой точки А этой прямой изменяется по закону

S(t) = 0,5t 2 + 3t + 8 (м),  где t (с) – время движения. Через какое время после начала движения скорость тела окажется  равной 15 м/с?

6. Точка движется прямолинейно по закону

s(t) = –t³ + 5t² + 4 (м). Найдите:

1.   скорость в момент времени t = 1 с;

2.   ускорение в момент времени t = 1 с;

3.   максимальную скорость движения этой точки.

4.   момент времени, в который скорость точки окажется равной нулю.

7. При каком значении аргумента равны скорости изменения функций                      f (x) = cos 2x   и    g(x) = sin x?

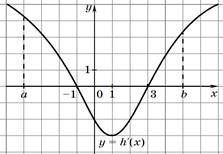
8. По графику производной y = h¢(x)  функции у = h(x),  изображенному на рисунке 1, укажите точки минимума и максимума функции у = h(x) на промежутке (а; b).

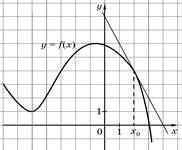
9. На рисунке 2 изображён график функции у = f(x) и касательная к нему в точке с абсциссой х₀. Найдите значение производной в точке х₀.

                                рис. 1                                                   рис. 2

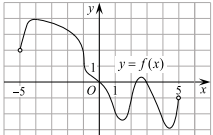10. На рисунке изображён график функции y = f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.

11. Найдите наименьшее значение функции  

у = 9     на отрезке .

12. Найдите первообразную  функции   f(x) = соs4x,  график которой проходит через точку (0;-1).

13.  Вычислить (предварительно сделав рисунок) площадь фигуры, ограниченной линиями:

у = х²  - 2х + 2   и  у = 2 + 4х - х².

14. Периметр осевого сечения цилиндра равен 36 см. Диагональ осевого сечения составляет с образующей цилиндра угол 45⁰. Найдите площадь боковой поверхности цилиндра.

1. Укажите убывающую на всей области определения функцию

        А) y = -x3;        Б) y = 5;         В) y = sin x;         Г) у =   .

2. Запишите уравнение касательной к графику функции

y = x 2 + 3x - 2 в его точке с абсциссой, равной 1.

3. Тело движется по прямой так, что расстояние s до него от некоторой точки А этой прямой изменяется по закону

движения  S(t)= 0,5t 2 + 5t - 2 (м), где t (с) – время

Через какое время после начала движения скорость тела окажется

равной 12 м/с?

4. Точка движется прямолинейно по закону

 s(t) = –t³ + 2t² – 4 (м).

Найдите:

1)   скорость в момент времени t = 3 с;

2)   ускорение в момент времени t = 1 с;

3)   максимальную скорость движения этой точки;

4)   момент времени, в который скорость точки окажется равной нулю.

5. Если значения         производной   во        всех     точках промежутка положительны, то функция на этом промежутке:

                             А) возрастает;         В) не изменяется;

                             Б)  убывает;             Г) другой ответ.

6. Если производная функции при переходе через точку х₀ меняет знак с плюса на минус, то в этой точке данная функция:

                             А)  имеет максимум;           В) убывает;

                             Б)  имеет минимум;              Г) другой ответ.

7. При каком значении аргумента равны скорости изменения функций                      f (x) = cos 2x   и    g(x) = sin x?

8. По графику производной  y = g¢(x),   изображённому на рисунке 1,

 укажите  точки минимума и  максимума функции у = g(x) на промежутке (а; b).

9. На рисунке 2 изображен график функции у = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной в точке х₀.

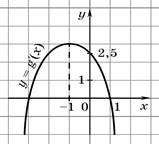
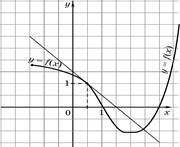
               рис. 1                                                  рис.2

10. На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.

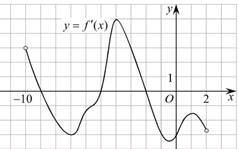11. Найдите наименьшее значение функции  у =  на отрезке  .

12. Найдите первообразную функции           

f(x) = sin2x, график которой проходит через точку (0; - 1).

13.  Вычислить (предварительно сделав рисунок) площадь фигуры, ограниченной линиями:

у = х²  + 1   и  у = - х² + 4х + 1.

14. Площадь осевого сечения цилиндра равна 18√3 см². Отрезок, соединяющий центр верхнего основания цилиндра с точкой окружности нижнего основания образует с осью цилиндра угол 30⁰. Найдите площадь боковой поверхности цилиндра.

Скачано с www.znanio.ru