
МИНОБРНАУКИ РОССИИ
федеральное государственное бюджетное образовательное учреждение высшего образования «Югорский государственный университет» (ЮГУ)
Лянторский нефтяной техникум
(филиал) федерального государственного бюджетного образовательного учреждения высшего образования «Югорский государственный университет»
(ЛНТ (филиал) ФГБОУ ВО «ЮГУ»)
Утверждаю
Заместитель директора по УР
ЛНТ (филиала) ФГБОУ ВО « ЮГУ»
________________/О. В. Кийдан/
«_______»____________20____ г.
Контрольно-оценочные средства
по учебной дисциплине
ЕН 01. Математика
23.02.01 Разработка и эксплуатация нефтяных и газовых месторождений
Лянтор 2020
Разработчик: Гимаметдинова Гульнара Шамилевна, преподаватель математики Лянторского нефтяного техникума (филиала) федерального государственного бюджетного образовательного учреждения высшего образования «Югорский государственный университет»
|
|
|||
|
|
1. Паспорт комплекта контрольно-оценочных средств
Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу дисциплины Математика.
КОС включают контрольные материалы для проведения промежуточной аттестации в форме экзамена.
КОС разработаны в соответствии с:
основной профессиональной образовательной программой по специальности СПО 21.02.01 Разработка и эксплуатация нефтяных и газовых месторождений
программой учебной дисциплины Математика.
2. Результаты освоения учебной дисциплины, подлежащие проверке
2.1. В результате аттестации по учебной дисциплине осуществляется комплексная проверка следующих умений и знаний, а также динамика формирования общих и профессиональных компетенций, если предусмотрено ФГОС:
У 1. Решать прикладные задачи в области профессиональной деятельности;
З 1. Значение математики в профессиональной деятельности и при освоении ППССЗ;
З 2.Основные математические методы решения прикладных задач в области профессиональной деятельности;
З 3. Основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;
З 4. Основы интегрального и дифференциального исчисления.
Таблица 1
|
Результаты обучения: умения, знания и общие компетенции |
Показатели оценки результата |
Форма контроля и оценивания |
|
У 1. Решать прикладные задачи в области профессиональной деятельности; З 1. Значение математики в профессиональной деятельности и при освоении ППССЗ; З 2.Основные математические методы решения прикладных задач в области профессиональной деятельности; З 3. Основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; З 4. основы интегрального и дифференциального исчисления. ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личного развития. ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности. ОК 7. Брать на себя ответственность за работу членов команды, за результат выполнения заданий. ОК 8. Самостоятельно определять задачи профессионального и личного развития, заниматься самообразованием, осознанно планировать повышение квалификации. ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности. повышение квалификации. ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
- применение и знание формулы в расчёте практической задачи - выбор технологии решения задачи. - знание терминологии. - описание процессов и явлений реального мира с помощью математических понятий - применение математических методов для решения содержательных задач из различных областей практики - определение путей формирования себя как специалиста с учетом индивидуальных особенностей личности. - уровень представления о выбранной профессии, ее значимости для общества - способность понимать цель, поставленную преподавателем и самостоятельно определять задачи для реализации цели; - способность выбирать типовые методы решения задач; - способность оценивать свою деятельность. - готовность самостоятельно принимать решения при решении проблем и задач, в учебных и деловых играх. - способность координировать деятельность членов коллектива. |
- устный или письменный опрос - тестовые задания - оценка выполнения практической работы. - |
|
У 1. Решать прикладные задачи в области профессиональной деятельности; З 3. Основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики; ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
- выбор технологии решения задачи. - знание терминологии. - вычисление пределов функции в точке и в бесконечности, выполнять операции над множествами, находить пересечение и объединение множеств, определять рефлексивные, транзитивные, симметричные отношения - решение задачи на нахождение числа размещений, перестановок и сочетаний - воспроизведение основных понятия теории вероятностей; - определение числовых характеристик дискретной случайной величины; - построение функции распределения. - вычисление статистических параметров распределения - уровень представления о выбранной профессии, ее значимости для общества - способность понимать цель, поставленную преподавателем и самостоятельно определять задачи для реализации цели; - способность выбирать типовые методы решения задач; - способность оценивать свою деятельность. - готовность самостоятельно принимать решения при решении проблем и задач, в учебных и деловых играх. - способность координировать деятельность членов коллектива. |
- устный или письменный опрос - тестовые задания - оценка выполнения практической работы. - |
|
У 1. Решать прикладные задачи в области профессиональной деятельности; З 4. основы интегрального и дифференциального исчисления. |
- применение и знание формулы в расчёте практической задачи. - выбор технологии решения задачи. - знание терминологии. - решение прикладных задач. формулировка правил дифференцирования и перечисление производных основных элементарных функций - характеристика понятия производной функции; - - описание правил дифференцирования функции; - исследование функции на непрерывность в точке - нахождение производной функции - нахождение производных высших порядков - исследование функции и построение графика - нахождение частных производных - перечисление табличных интегралов - нахождение неопределенных интегралов - вычисление определенных интегралов - использовать приближенные методы вычисления определенных интегралов - формулировка классического определения вероятности - исследование рядов на сходимость - применение различных методов для решения дифференциальных уравнений первого и второго порядка. - уровень представления о выбранной профессии, ее значимости для общества - способность понимать цель, поставленную преподавателем и самостоятельно определять задачи для реализации цели; - способность выбирать типовые методы решения задач; - способность оценивать свою деятельность. - готовность самостоятельно принимать решения при решении проблем и задач, в учебных и деловых играх. - способность координировать деятельность членов коллектива. |
- устный или письменный опрос - тестовые задания - оценка выполнения практической работы. - |
3. Описание правил оформления результатов оценивания
Предметом оценки служат умения и знания, предусмотренные ФГОС по дисциплине Математика, направленные на формирование общих и профессиональных компетенций. Оценка курса учебной дисциплины предусматривает наличие положительной оценки по всем формам текущего контроля знаний:
- устного или письменного опроса
- тестовых заданий
- оценки выполнения практических работ
Таблица 2.
3.1. Контроль и оценка освоения учебной дисциплины по темам (разделам), видам контроля
|
Элемент учебной дисциплины |
Формы и методы контроля |
|||
|
Текущий контроль |
Промежуточная аттестация |
|||
|
Форма контроля |
Проверяемые ОК, ПК (или ее части), У, З |
Форма контроля |
Проверяемые ОК, ПК (или ее части),У, З |
|
|
Раздел 1. Введение в анализ |
Экзамен
|
У1 З1 З2 З3 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
||
|
Тема 1.1. Дифференциальное и интегральное исчисление |
Самостоятельная работа №1 Самостоятельная работа №2 Письменный опрос№1 Письменный опрос№2 Устный опрос №1 Устный опрос №2 Устный опрос №3 Практическая работа №1 Практическая работа №2 Практическая работа №3 Практическая работа №4 |
У1 З1 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
|
|
|
Тема 1.2. Ряды |
Самостоятельная работа №3 Расчетное задание№3 |
У1 З3 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
|
|
|
Тема 1.3. Дифференциальное исчисление функций нескольких переменных |
Письменный опрос№4 |
У1 З1 З2 З3 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
||
|
Тема 1.4. Обыкновенные Дифференциальные уравнения |
Самостоятельная работа№4 Самостоятельная работа№5 Письменный опрос№5 Письменный опрос№6 Письменный опрос№7 Устный опрос №4 Практическая работа №5 Практическая работа №6 |
У1 З1 З2 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
|
|
|
Тема 1.5. Комплексные числа |
Самостоятельная работа№6 Устный опрос №5 Устный опрос №6 Практическая работа №7 Практическая работа №8 |
У1 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
||
|
Раздел 2. Дискретная математика |
Экзамен
|
У1 З2 З3 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
||
|
Тема 2.1. Основы дискретной математики |
Письменный опрос №8 |
У1 З1 З2 З3 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
|
|
|
Раздел 3. Численные методы |
Экзамен
|
У1 З2 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
||
|
Тема 3.1. Основы численных методов алгебры |
Самостоятельная работа№7 Устный опрос №7
|
У1 З1 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
|
|
|
Раздел 4. Теория вероятностей и математическая статистика |
Экзамен
|
У1 З1 З2 З3 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
||
|
Тема 4.1. Теория вероятностей |
Самостоятельная работа№8 Письменный опрос№9 Письменный опрос №10 Устный опрос №8 Устный опрос №9 Практическая работа №9 Практическая работа №10 |
У1 З1 З2 З3 З4 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
|
|
|
Тема 4.2. Математическая статистика |
Самостоятельная работа№9 Письменный опрос№11 Устный опрос №10 Практическая работа №11 |
У1 З2 З3 ОК 1-5, ОК 7-9 ПК 1.1- 1.4, ПК 2.1, ПК2.5, ПК 3.1, ПК 3.3 |
|
|
4. Комплект оценочных средств
4.1. Задания промежуточной аттестации
Таблица 4
Перечень объектов контроля и оценки
|
Предмет оценивания |
Объекты оценивания |
Показатель оценки |
Критерии оценки |
|
У 1. Решать прикладные задачи в области профессиональной деятельности З1. Значение математики в профессиональной деятельности при освоении ППССЗ; З2. Основные математические методы решения прикладных задач в области профессиональной деятельности; |
Обязательная часть Задание 1. Задание 2. Задание 3. Задание 4. Задание 5. Задание 6. Задание 7. Задание 8. Задание 9. Задание 10.
Дополнительная часть с теоретическим заданием Задание 11 Задан Задание 12 Задание 13 Задание 14 Задание 15 |
- применение и знание формулы в расчёте практической задачи - выбор технологии решения задачи. - знание терминологии. - описание процессов и явлений реального мира с помощью математических понятий - применение математических методов для решения содержательных задач из различных областей практики |
За правильное выполнение любого задания из обязательной части обучающийся получает -1 балл. При выполнении задания из обязательной части, где необходимо привести краткое решение, за неполное решение задания (вычислительная ошибка, описка) можно выставить 0,5 балла. Если обучающийся приводит наверное решение, неверный ответ или не приводит никакого ответа он получает 0 баллов. За выполнение любого задания из дополнительной части с теоретическим заданием можно использовать следующие критерии оценки заданий: Приведено верное обоснованное решение, приведен правильный ответ -2 балла Приведено верное решение, но допущена вычислительная ошибка или описка, при этом может быть получен неверный ответ -1 балл Неверное решение, неверный ответ или отсутствие решения -0 баллов |
|
З 3. Основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятности и математической статистики; |
- вычисление пределов функции в точке и в бесконечности, выполнение операций над множествами, нахождение пересечений и объединений множеств, - решение задачи на нахождение числа размещений, перестановок и сочетаний - воспроизведение основных понятия теории вероятностей; - определение числовых характеристик дискретной случайной величины; - построение функции распределения. - вычисление статистических параметров распределения |
||
|
З4. Основы интегрального и дифференциального исчисления. |
- применение и знание формулы в расчёте практической задачи. - выбор технологии решения задачи. - знание терминологии. - решение прикладных задач. - формулировка правил дифференцирования и перечисление производных основных элементарных функций - характеристика понятия производной функции; - - описание правил дифференцирования функции; - исследование функции на непрерывность в точке - нахождение производной функции - нахождение производных высших порядков - исследование функции и построение графика - нахождение частных производных - перечисление табличных интегралов - нахождение неопределенных интегралов - вычисление определенных интегралов - использовать приближенные методы вычисления определенных интегралов - формулировка классического определения вероятности - исследование рядов на сходимость - применение различных методов для решения дифференциальных уравнений первого и второго порядка. |
4.1.1 Задание 1. Вычислите определенный интеграл
1.
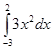
2.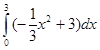
3.![]()
4.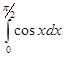
5.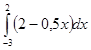
6.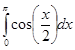
7.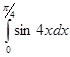
8.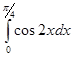
Задание 2. Найти неопределенный интеграл
1.![]()
2.![]()
3.![]()
4.![]()
5.![]() .
.
6.![]()
7.![]() .
.
Задание 3. Найти производную функции
1. ![]()
2.![]()
3. ![]()
4.![]()
5.![]()
6.![]()
7.![]()
8.![]()
Задание 4 Применение производной
1.
Найдите
ускорение в указанные моменты времени для точки, движущейся прямолинейно, если
движение точки задано уравнением ![]() ,
,
2.
Найдите
скорость в указанные моменты времени для точки, движущейся прямолинейно, если
движение точки задано уравнением ![]() ,
, ![]() .
.
3.
Найдите
ускорение в указанные моменты времени для точки, движущейся прямолинейно,
если движение точки задано уравнением ![]() ,
, ![]() .
.
Задание 5 Решите дифференциальное уравнение
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
Задание 6 Вычисление элементов комбинаторики
1. 5! + 6!
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
Задание 7 Исследовать сходимость ряда
1.
Исследовать
сходимость ряда, используя признак Даламбера ![]()
2.
Установить
расходимость ряда ![]() с помощью
достаточного признака расходимости ряда.
с помощью
достаточного признака расходимости ряда.
3.
Используя
признак Даламбера, исследовать на сходимость ряд ![]()
4. Используя признак
Даламбера, исследовать на сходимость ряд ![]()
5.
Используя
признак Коши, исследовать на сходимость ряд ![]() ;
;
6.
Используя
признак Коши, исследовать на сходимость ряд ![]()
7.
Установить
расходимость ряда ![]() с помощью
достаточного признака расходимости ряда.
с помощью
достаточного признака расходимости ряда.
8.
Используя
признак Даламбера, исследовать на сходимость ряд ![]()
9.
Используя
признак Даламбера, исследовать на сходимость ряд ![]()
10.
Используя
признак Коши, исследовать на сходимость ряд ![]() ;
;
11.
Используя
признак Коши, исследовать на сходимость ряд ![]()
Задание 8 Дифференцирование функций двух переменных
1.
Вычислите
полный дифференциал функции ![]() в точке М(1; 2)
в точке М(1; 2)
2. Найти частные производные функций z=x3+3xy2–y3
3.
Найти
частные производные функций z=![]()
4. Найти частные производные функций z=x3–5x2y+y2
5.
Найти
частные производные функций z=![]()
6.
Найти
значения частных производных функций в заданных точках z=![]() в точке М(1;2)
в точке М(1;2)
7.
Найти
значения частных производных функций в заданных точках z=![]() в точке М(2;1)
в точке М(2;1)
8.
Вычислите
полные дифференциалы функций в заданных точках z=![]() при x=1, y=2, dz=0,2; dy=0,1
при x=1, y=2, dz=0,2; dy=0,1
9.
Вычислите
полные дифференциалы функций в заданных точках
z=![]() при x=1, y=2, dz=
при x=1, y=2, dz=![]() ; dy=–
; dy=–![]()
Задание 9 Комплексные числа .Найти модуль комплексного числа и сопряженное.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
Задание 10 Множества и действия над множествами

|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
![]()
|
1 |
|
|
2 |
|
|
3 |
|
|
4 |

|
1 |
|
|
2 |
|
|
3 |
|
|
4 |

|
1 |
|
|
2 |
|
|
3 |
|
|
4 |

|
1 |
|
|
2 |
|
|
3 |
|
|
4 |

|
1 |
|
|
2 |
|
|
3 |
|
|
4 |
Задание 11 Вычисление пределов
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. 
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.