Кривые третьего порядка

 

Выполнила Ахметдинова Виктория Александровна

 

 

Введение

 

Понятие линии возникло в сознании человека в доисторические времена. Траектория брошенного камня, очертания цветов и листьев растений, извилистая линия берега реки и другие явления природы с давних пор привлекали внимания людей. Наблюдаемые многократно, они послужили основой для постепенного установления понятия о линии. Но потребовался значительный промежуток времени для того, чтобы наши предки стали сравнивать между собой формы кривых линий. Первые рисунки на стенах пещер, примитивные орнаменты на домашней утвари показывают, что люди умели не только отличать прямую от кривой, но и различать отдельные кривые. Памятники глубокой древности свидетельствуют о том, что у всех народов на некоторой степени их развития имелись понятия прямой и их окружности. Для построения этих линий использовались простейшие инструменты.

Однако лишь с возникновением математических теорий стало развиваться учение о линиях. Греческие ученые создали теорию линий второго порядка. Эти линии рассматривались как сечение конуса плоскостью, вследствие чего в древности их называли коническими сечениями. Конические сечения впервые рассматривал Менехм, который жил в IV веке до н.э..Первое систематическое изложение теории этих линий дал Аполлоний Пергский (III–II вв до н.э.) у своем сочинении «Конические сечения», которое почти целиком дошло до нас. В поисках решения различных задач греческие ученые рассматривали и некоторые трансцендентные линии.

В средневековую эпоху важное достижение греческих ученых были забыты. Математическая наука снова обратилась к изучению кривых только в VII веке. Для исследования линий первостепенное значение имело открытее Декартом и Ферма метода координат способствовавшего возникновению исчисления бесконечно малых. Метод координат в соединении с анализом бесконечно малых позволил перейти к исследованию линий общим способом. Разнообразные проблемы механики, астрономии, геодэзии, оптики, возникши в VII–VIII века, привели к открытию многих новых линий и изучению их геометрических механических свойств. Этими вопросами с большим энтузиазмом занимались крупнейшие математики эпохи – Декарт, Гюйгенс, Лейбниц, братья Бернулли.

Актуальность данной темы в том, что в разных разделах математики и на разных этапах изучения мы встречаемся с кривыми, как третьего, так и второго порядка. Но, нигде не говорится о замечательных свойствах данных кривых, а тем более об их практическом применении.

Основной целью данной работы является исследование кривых третьего порядка методами дифференциальной геометрии.

 Для реализации поставленной цели были сформулированы следующие задачи:

1)    проанализировать научную и учебную литературу по теме курсового исследования с целью выделения основных понятий и утверждений;

2)    систематизировать и обобщить материал по теме курсового исследования;

3)    доказать необходимые утверждения в теме курсового исследования;

4)    исследовать кривые третьего порядка методами дифференциальной геометрии по их основным уравнениям.

Основным методом исследования стал теоретический анализ литературы в рамках исследования.

Практическая значимость определяется возможностью использования результатов данного исследования в учебном процессе в вузе в курсе дисциплины  «Дифференциальная геометрия».

 

 

Глава 1. Кривые третьего порядка

 

Кубика - плоская кривая 3-го порядка, т. е. множество точек плоскости (проективной, аффинной, евклидовой), однородные координаты х ₀, x₁, x₂ которых удовлетворяют однородному уравнению третьей степени. 

Общее уравнение кривой третьего порядка

При помощи элементарных преобразований Ньютон приводит общее уравнение кривой к одной из четырех форм:

A.

B.

C.

D.

Далее мы берем коэффициенты канонического уравнения и составляем вспомогательное уравнение 4-й (или 3-й) степени:

 или , которое можно назвать характеристическим. В зависимости от различных соотношений между корнями характеристического уравнения Ньютон делит все кривые 3-го порядка на 7 классов, 14 родов, 72 типа.

Кривые, уравнения которых приводятся к канонической форме A, Ньютон делит на четыре класса: гиперболические гиперболы (a>0), дефективные гиперболы (a<0), параболические гиперболы (a=0, b=0), гиперболизмы конических сечений (a=b=0).

Гиперболические гиперболы делятся на четыре рода: адиаметральные – без диаметров (е≠0), монодиаметральные – с одним диаметром (е=0, , тридиаметральные (е=0, , гиперболические гиперболы с асимптотами, пересекающимися в одной точке (b=0).

Классы дефективных и параболических гипербол состоят из двух родов каждый: адиаметральных (е≠0), монодиаметральных (е=0).

Гиперболизмы конических сечений делятся на три рода: гиперболизмы гиперболы (с>0), гиперболизмы эллипса (c<0) и гиперболизмы параболы (с=0).

Классификация Ньютона

 

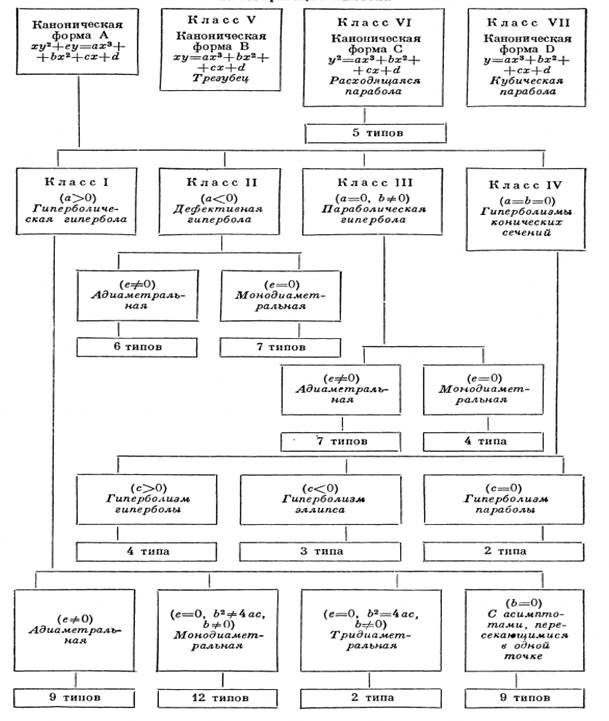
Кривые, уравнения которых приводятся к каноническим формам B, C, D, представляют соответственно по одному классу: трезубец или параболизм гиперболы, расходящаяся парабола (этот класс делится на пять типов) и кубическая парабола.

 

 

Глава 2. Частные случаи линий третьего порядка

 

2. 1. Декартов лист

 

1. Историческая справка. Впервые в истории математики кривая, названная впоследствии декартовым листом, определяется в письме Декарта к Ферма в 1638 г. как кривая, для которой сумма объемов кубов, построенных на абсциссе и ординате каждой точки, равняется объему параллелепипеда, построенного на абсциссе, ординате и некоторой константе. Первым Роберваль устанавливает форму кривой, который находит узловую точку кривой, однако в его представлении кривая состоит лишь из петли. Повторяя эту петлю в четырех квадрантах, он получает фигуру, напоминающую ему цветок с четырьмя лепестками. Поэтическое название кривой “лепесток жасмина”, не прижилось. Гюйгенс и И. Бернулли в 1692 году определили полную форма кривой с наличием асимптоты. И лишь с начала 18 века установилось название “декартов лист”, которое мы и употребляем до сих пор.

2. Особенности формы. Декартовым листом называется кривая 3-го порядка, уравнение которой в прямоугольной системе имеет вид

                 (1)

В некоторых случаях удобно пользоваться параметрическими уравнениями декартова листа, которые можно получить присоединяя к y=tx равенству равенство (1) и решая полученную систему относительно х и у, в результате получим систему вида:

                                  (2)

Из нее сделаем вывод о том, что декартов лист является рациональной кривой.

Отметим, что       полярное уравнение декартова листа имеет вид

                      (3)

Координаты х и у входят в уравнение декартова листа симметрично, отсюда следует, что кривая симметрична относительно биссектрисы у=х. Если исследовать на особые точки, то при­дем к заключению, что начало координат является узловой точкой декартова листа. Уравнения касательных к алгебраической кривой в ее особой точке, совпадающей с началом координат, можно получить, приравнивая нулю группу членов низшей степени из уравнения этой кривой. Итак, имеем 3ху = 0, откуда получим        х = 0 и у = 0 – искомые уравнения касательных в узловой точке. Эти касательные совпадают с координатными осями, следовательно, в начале координат кривая пересекает сама себя под прямым углом. В первом координатном угле кривая делает петлю, которая пересекается с прямой у = х в точке

Точки этой петли, в которых касательные параллельны координатным осям, имеют координаты

 и  ( рис. 1)

Для окончательного заключения о форме кривой нужно найти асимптоту Если заменить в уравнении кривой у на  и приравнять к нулю в полученном уравнении коэффициенты двух членов с высшими степенями х, получим  и , откуда  и b = - а. Таким образом, декартов  лист имеет асимптоту у = - х - а; а это значит, что во 2-м и 4-м координатных углах ветви декартова листа уходят в бесконечность.

 

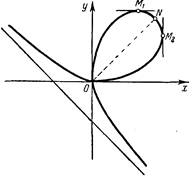
Рис. 1

3. Свойства. По теореме Маклорена, если в трех точках алгебраической кривой 3-го порядка, лежащих на одной прямой, провести касательные к этой кривой, то точки их пересечения с кривой будут лежать также на прямой линии. Применим к декартову листу и докажем.

Предварительно выведем с этой целью условие пребывания трех точек декартова листа, соответствующих значениям t₁ , t₂ и t₃ параметра, на одной прямой. Если уравнение прямой имеет вид y=kx+b, то значения параметра, соответствующие точкам пересечения этой прямой с кривой, должны удовлетворять системе

, ,

Система эта приводит к уравнению

, корни которого и будут искомыми значениями t₁ , t₂ и t₃ параметра, откуда следует, что

t₁t₂t₃=-1                         (4)

Это равенство и является условием пребывания трех точек M₁(t₁ ), M₂(t₂), М₃ (t₃) декартова листа на одной прямой.

Теперь покажем справедливость теоремы Маклорена для декартово листа. Действительно, касательную в точке M₁ (t₁) можно рассматривать как прямую, которая пересекает декартов лист в двух совпадающих между собой точках, для которых t₂=t₁, и в третьей точке, для которой соответствующее значение параметра обозначим через T₁. Условие (4) примет вид t₁² T₁= -1. Для касательных в точках М₂ и M₃ получим соотношения t₂² T₂ = -1 и            t₃² T₃ = -1. Перемножая эти три равен­ства, получим (t₁t₂t₃)²T₁T₂T₃ = -1. На основании (4) заключаем, что и T₁T₂T₃ = -1, т. е. точки N₁(T₁), N₂(T₂) и N₃(T₃) лежат на одной прямой.

Определяя площадь, ограниченную петлей декартова листа, получим:

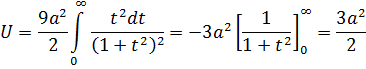
4. Способ построения. Необходимо уесть, что если ось симметрии декартова листа принять за ось абсцисс, то уравнение его примет вид

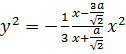             (5)

Пусть имеется окружность с радиусом r и центром в точке и прямая х= -h. Возьмем произвольную точку Q этой окружности и проведем прямую QA и прямую QN, перпендикулярную к оси абсцисс (рис. 2). Из точки пересечения R прямой QA с прямой  х= -h проводим прямую RO до пересечения ее в точке Q₁ с прямой QN. Таким образом, точке Q на окруж­ности поставлена в соответствие точка Q₁. Геометрическое место точек Q₁ представляет собой декартов лист.

Рис 2.

Для того, чтобы доказать, заметим, что координаты точки Q можно записать в виде

, где  – угол, составляемый радиусом круга, проведенным в точку Q, с положительным направлением оси абсцисс. С учетом этого уравнение прямой QA может быть записано в виде

Представим в этом уравнении х= -h, находим ординату

точки R. Отсюда следует, что уравнение прямой RQ₁  запишется в виде

                    (6)

Но также уравнение прямой Q₁N имеет вид

               (7)

Исключая из уравнений (6) и (7) параметр w, находим уравнение гео­метрического места точек Q₁ в виде

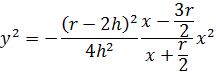
А сопоставляя его с уравнением (5), делаем вывод, что найденное геомет­рическое место точек является декартовым листом.

Преобразование точек окружности в точки декартова листа, осу­ществляемое при таком его построении, называется преобразованием Маклорена.

 

2. 2. Циссоида Диоклеса

 

1. Особенности формы. Среди многих способов образования циссоиды—кривой, открытой древними в поисках решения знаменитой задачи об удвоении куба, мы остановимся для начала на более простейшем. Возьмем окружность (называемую производящей) с диаметром ОА=2а и касательную АВ к ней. Через точку О проведем луч ОВ и на нем отложим отрезок ОМ=ВС. Тогда точка М принадлежит циссоиде. Повернув луч 0В на некоторый угол и проделав указанное построение, мы найдем вторую точку

циссоиды, и т. д. (Рис. 3).

Если точку О принять за полюс, то , но  и  откуда получаем полярное уравнение циссоиды

                    (1)

Воспользуемся формулами перехода от полярных координат к декартовым, и найдем уравнение циссоиды в прямоугольной системе:

             (2)

Параметрические уравнения циссоиды можно получить, заменив x=ty, тогда, из уравнения (2), придем к системе:

,     (3)

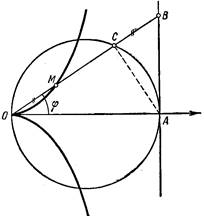
Рис. 3

Уравнение (2) показывает, что циссоида является алгебраической кривой 3-го порядка, а из уравнений (3) следует, что она является рациональной кривой.

Циссоида симметрична относительно оси абсцисс и имеет бесконечные ветви; касательная к производящей окружности, т. е. прямая х = 2а, служит для нее асимптотой; начало координат является точкой возврата 1-го рода.

2. Свойства. Кинематически циссоида может быть получена как траектория середины М катета ВС треугольника АВС, передвигающегося в плоскости чертежа так, что его вершина В скользит по оси ординат, а другой катет АС всегда проходит через неподвижную точку Е на оси абсцисс.
 (Рис. 4)

Действительно, если мы обозначим середину отрезка ОЕ через D, то заметим, что поскольку ВС=ЕО, ê ВСЕ=ê ВЕО, откуда ВЕО = СВЕ, тогда, ê NBE— равнобедренный, а так как  ЕD=ЕО/2=ВС/2=ВМ, то отрезок DM параллелен отрезку BE. Теперь пусть точка К есть точка пересечения с продолжением отрезка DM прямой, проходящей через точку В параллельно оси абсцисс. Опишем окружность с центром в начале координат и радиусом, равным OD, и проведем к ней касательную во второй точке пересечения с прямой ЕО. Она пройдет через точку К. Если обозначить точку пересечения прямой DMK с окружностью через F, получим, что треугольники DOF и МВК равны между собой. Из равенства их следует, что DF=MK, а значит, и DM=FK. Из последнего равенства видно, что геометрическое место точек М будет циссоидой.

Рис. 4.

Есть и другие способы образования циссоиды, которые основаны на ее соотношениях с параболой. Покажем в первую очередь, что циссоида является подэрой параболы относительно ее вершины.

Пусть   – уравнение данной параболы. Уравнение касательной в произвольной точке М (x, h) этой параболы можно записать в виде
   уравнение перпендикуляра, опущенного из начала координат на эту касательную, будет  координаты точки N пересечения его с касательной определятся по формулам

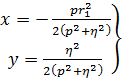             (4)

Исключая из этих равенств параметр h, мы получим уравнение
  выражающее циссоиду.

Также заметим, что координаты точки, симметричной началу коор­динат относительно касательной к параболе у² = 2рх, получатся, если правые части формул (4) удвоить, и, следовательно, определятся формулами

 и

Исключая из этих равенств параметр h, мы снова получим циссоиду с уравнением . Тогда циссоида является геометрическим местом точек, симметричных вершине параболы относительно ее касательных.

Нужно отметить, что геометрическое место точек, симметричных началу координат относительно касательной к параболе, можно рас­сматривать как траекторию вершины другой параболы, одинаковой с данной, которая катится по данной параболе. Отсюда возникает новый способ кинематического образования циссоиды как траектории вершины параболы, которая без скольжения катится по другой такой же параболе.

Остановимся на метрических свойствах циссоиды; при этом нам будет удобно пользоваться параметрическими уравнениями циссоиды в виде

,

Площадь, ограниченная циссоидой и ее асимптотой, равняется утроенной площади производящего круга; действительно,

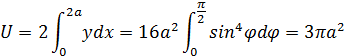
Это соотношение получено было Гюйгенсом и независимо от него Ферма.

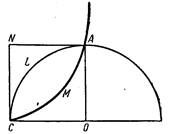
Рис. 5.

Определяя площадь криволинейного треугольника ОАМС (рис.5), найдем, интегрируя в границах от  до   что она равна . Если теперь провести касательные в точках А и С к производящему кругу, то площадь криволинейного треугольника CMANC будет равна
 

 Выражение, стоящее в правой части, определяет утроенную площадь криволинейного треугольника CLANC. Итак, площадь CMANC =3 площади CLANC. Это соотношение было открыто также Гюйгенсом.

Объем тела, образованного вращением части плоскости, ограниченной циссоидой и ее асимптотой, вокруг оси ординат определится по формуле

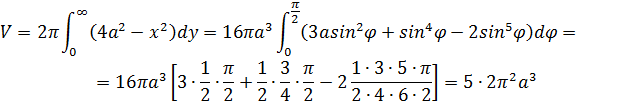
Если учесть, что объем тора, получаемого от вращения производя­щего круга вокруг оси ординат, равняется то из полученного результата следует, что объем тела, получаемого вращением части плоскости, ограниченной циссоидой и ее асимптотой, вокруг оси ординат, в пять раз больше объема тора, полученного от вра­щения производящего круга вокруг той же оси. Это соотношение было получено также Гюйгенсом.

Пусть теперь х_с — абсцисса центра тяжести части плоскости, ограниченной циссоидой и ее асимптотой; тогда по теореме Гюльдена будем иметь V = U  2pх_с, где V и U—соответственно объем и площадь, которые были определены выше. Подставляя их значения в соотношение Гюльдена, получим  или  

Тогда, центр тяжести части плоскости, ограни­чиваемой циссоидой и ее асимптотой, делит отрезок между вершиной и асимптотой на две части, отношение которых равно 5.

Это соотношение позволяет в свою очередь определить объем тела, полученного вращением циссоиды вокруг ее асимптоты. По теореме Гюльдена будем иметь

Данный результат можно истолковать также как объем тора, полученного от вращения производящего круга вокруг асимптоты. Тогда, объем тела, полученного вращением циссоиды вокруг ее асимптоты, будет равен объему тора, полученного от вращения производящего круга. Слюз впервые установил данное соотношение.

Длина дуги циссоиды от ее вершины до точки с абсциссой х определится по формуле

,

где

3. Применение циссоиды к решению делосской задачи. Циссоида была открыта древними в поисках решения делосской задачи об удвоении куба. История возникновения этой задачи, согласно легенде, передаваемой Эратосфеном, такова: на острове Делосе жители страдали от мора, посланного им богами; по предсказанию оракула богов можно было умиротворить, удвоив объем жертвенника, имевшего форму куба. Суть задачи сводилась к определению ребра куба, объем которого был бы в два раза больше объема данного куба. Что касается самого повода постановки задачи, то справедливо полагать, что “пифия находилась скорее под внушением математиков, нежели вдохновлялась самим богом” (Цейтен), так как задача об удвоении куба являлась естественным перенесением в пространство планиметрической задачи о построении квадрата с площадью, в два раза большей площади данного квадрата, и, следовательно, могла скорее возникнуть в сознании математика, нежели в сознании оракула.

Открытие циссоиды для целей решения делосской задачи при­писывается Диоклесу, жившему в 3 веке до нашей эры. Возможность найти графическим путем ребро куба с объемом, в два раза большим объема данного куба, усматривается из следующих соображений. Пусть b – ребро данного куба, а В – ребро искомого; тогда  и, следовательно,  Отсюда ясно, что графическое решение задачи должно свестись к построению  

Перепишем для этой цели уравнение циссоиды в виде  Заметим далее, что прямая   отсекает от касательной отрезок (рис. 6)

   (5)

и пересекает циссоиду в точке М, координаты которой удовлетворяют уравнению

Это уравнение можно рассматривать как уравнение прямой, проходящей через точку А (2а, 0) и отсекающей на оси ординат отрезок

          (6)

Если теперь принять  и на оси ординат отложить отрезок ОС= 2, соединить затем точку С с точкой А(1, 0), а точку пересечения прямой СА с циссоидой соединить с точкой О и продолжить полученный отрезок до пересечения с касательной, то, как это следует из формул (5) и (6), отрезок AD и будет равен  

Древние рассматривали только ту часть циссоиды, которая нахо­дится внутри производящего круга. Вместе с дугой окружности производящего круга эта часть образует фигуру, напоминающую лист плюща, откуда проистекает название кривой. Наличие бесконечных ветвей у циссоиды было установлено в 17 веке Робервалем и независимо от него Слюзом. Кинематический способ образования циссоиды с помощью треугольника приписывается Ньютону, который выполнил также спрямление циссоиды не только аналитическим путем, но и графическим.

 

2. 3. Локон Аньези

 

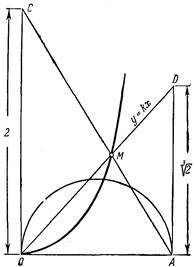
Пусть имеется круг с диаметром OC = -а и отрезок BDM, построенный так, что ОВ : BD = OC : ВМ; геометрическое место точек М представляет собой локон Аньези (или верзиеру). уравнение в прямоугольных координатах: у = a³/(a² + x²). Исследование этой кривой связано с именем итальянской женщины-математика Марии Аньези (1748).

Аньéзи Мария Гаэтана (Agnesi Maria Gaetana), родилась 16.05.1718, Милан - умерла 09.01.1799, там же. Сочинение Аньези "Основания анализа для употребления итальянского юношества" содержит изложение аналитической геометрии, в частности там рассмотрена кривая третьего порядка, названная "локоном Аньези" (или верзиера), уравнение которой y=a³ / (x² +a²) .

Для построения данной линии нужно нарисовать окружность радиусом a с центром в точке (0,a). Затем из начала координат провести прямые и отметить две точки. Точка А(x1, y1) - точка пересечения прямой и окружности, точка B(x2,2a) точка пересечения прямой и верхней горизонтальной касательной к окружности. Затем нужно построить точку кривой (x2,y1).

 

2. 4. Строфоида

 

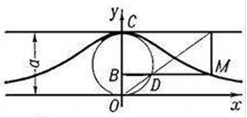
Строфоида (от греч. stróphos — кручёная лента и éidos — вид)

Пусть имеется неподвижная прямая АВ и точка С вне её на расстоянии CO = а; вокруг С вращается прямая, пересекающая АВ в переменной точке N. Если от точки N отложить по обе стороны прямой АВ отрезки NM = NM' = NO, то геометрическое место точек М и М' для всех положений вращающегося луча CN и есть строфоида. Уравнение в прямоугольных координатах:

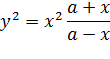
в полярных координатах:

r = —a cos 2j/cosj.

Уравнение строфоиды в полярной системе координат:

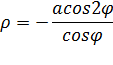
Параметрическое уравнение строфоиды:

,

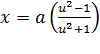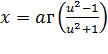
где .

Площадь петли строфоиды слева от оси ординат

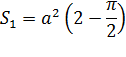
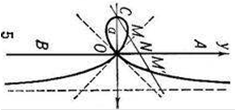
Площадь между строфоидой и асимптотой справа от оси ординат

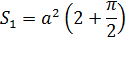
Считается, что строфоида впервые была рассмотрена французским математиком Жилем Робервалем в 1645 году. Роберваль называл эту кривую — «птероида» (от греч. πτερον— крыло). Название «строфоида» было введено в 1849 году.

 

 

Глава 3. Исследование линий третьего порядка методами дифференциальной геометрии

 

Исследовать линию – значит выявить совокупность важнейших свойств линии, позволяющих достаточно точно простроить ее. К важнейшим свойствам можно отнести наличие или отсутствие особых точек, точек перегиба, асимптот, точек самопересечения, точек, в которых касательные параллельны координатным осям и в которых линия пересекает эти оси.

Задание 1.

Исследуйте и постройте линий (с особыми точками), заданные уравнениями.

1. Ось симметрии ОХ.

2. Найдем особые точки. То есть те точки, в которых определяющие функции либо не удовлетворяют условиям регулярности, либо вообще не дифференцируемы.

Точка М(0, 0) не принадлежит линии. Значит особых точек нет.

3. Линия пересекает ось ОХ в точке .

Линия пересекает ось OY в точке .

4. Найдем асимптоты линии.

Исследуем сначала наклонные асимптоты.

Подставляя уравнение асимптоты , получаем

Приравнивая коэффициенты при двух старших членах нулю, находим параметры асимптоты. Получаем, наклонных асимптот нет.

Рассмотрим вертикальную асимптоту. Подставляем в исходное уравнение , получаем:

Вертикальных асимптот нет.

5. Уравнение касательной к линии.

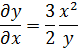
В т.  касательная параллельна оси ОY.

В т. . касательная параллельна оси ОХ.

Построим линию.

 

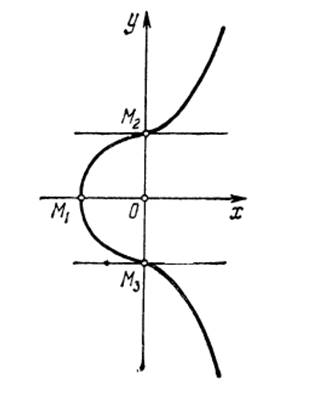
Задание 2.

Найти асимптоты линии:

Исследуем сначала наклонные асимптоты.

Подставляя уравнение асимптоты , получаем

Приравнивая коэффициенты при двух старших членах нулю, получим:

, тогда , . Уравнение .

, тогда , . Уравнение .

Получим наклонные асимптоты:

Рассмотрим вертикальную асимптоту. Подставляем в исходное уравнение , получаем:

Получаем .

Уравнение вертикальной асимптоты .

 

Задание 3.

Найти особые точки линии

 

Найдем производные первого порядка.

 

Получаем

 и  особые точки.

Найдем производные второго порядка.

Рассмотрим точку

Но точка  не принадлежит линии.

Рассмотрим точку . Точка принадлежит линии.

Найдем производные.

Значит точка  является точкой самопересечения. То есть так называемой узло- узловой точкой.

 

Задание 4.

Найти асимптоты декартова листа, заданного уравнением

 

Исследуем сначала наклонные асимптоты данной кривой. Запишем неявное уравнение в виде

Подставляя уравнение асимптоты  получаем:

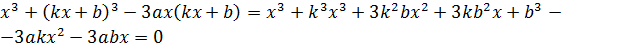
Приравнивая коэффициенты при двух старших членах нулю, находим параметры асимптоты k и b:

    

Таким образом, декартов лист имеет наклонную асимптоту, которая описывается уравнением. Проверим возможность существования вертикальной асимптоты. Пусть ее уравнение записывается как

Подставим это в исходное неявное уравнение кривой:

 

     

Заметим, что в последнем равенстве присутствует слагаемое в старшей степени y3. Это означает, что необходимое условие существования вертикальной асимптоты не выполняется. Следовательно, декартов лист имеет лишь наклонную асимптоту, найденную выше.

 

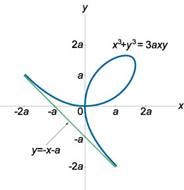
Задание 5. Циссоида Диоклеса.

1.     Определим параметризацию.

.

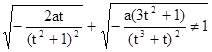Линия задана в произвольной параметризации.

2.     Найдем производные до третьего порядка.

   

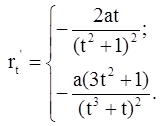
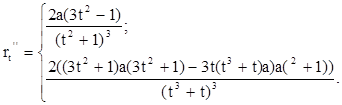
3.      Уравнение касательной:

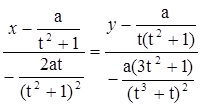
4.     Уравнение нормали:

 

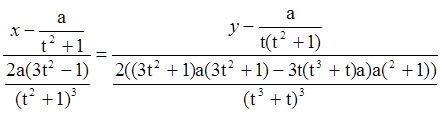
5.      Уравнение бинормали:

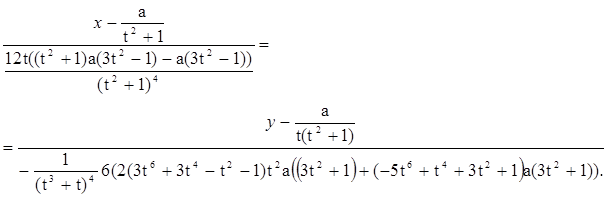
6.     Уравнение соприкасающейся плоскости:

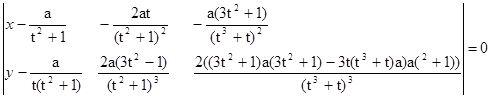
7.     Спрямляющая плоскость:

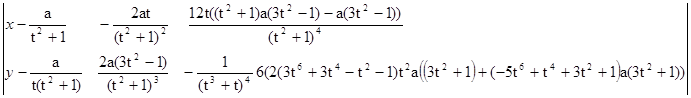
8.     Кривизна:

 

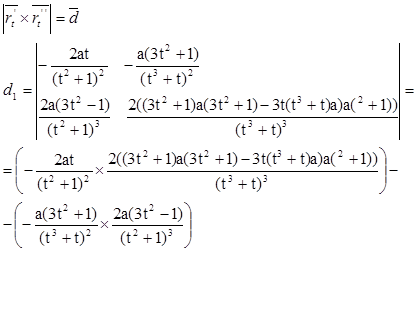
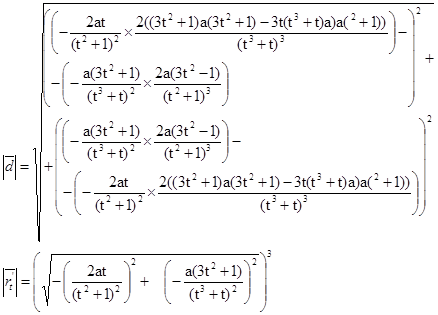
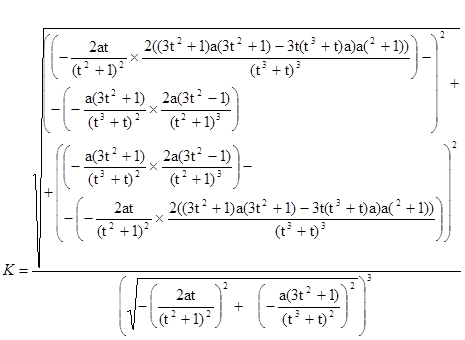
Задание 6. Декартов лист.

1.     Определим параметризацию.

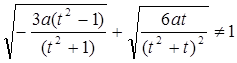
Линия задана в произвольной параметризации.

2.     Найдем производные до третьего порядка включительно:

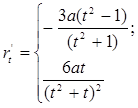
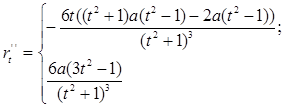
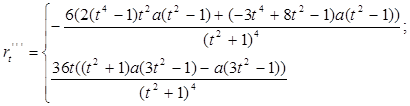
3.     Уравнение касательной:

                                       

 

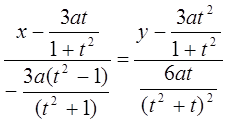
4.     Уравнение нормали:

5.     Уравнение бинормали:

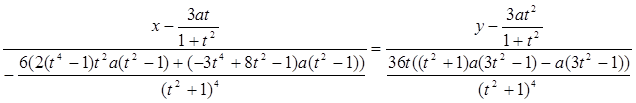
6.     Уравнение соприкасающейся плоскости:

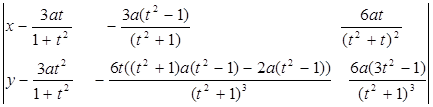
7.     Спрямляющая плоскость:

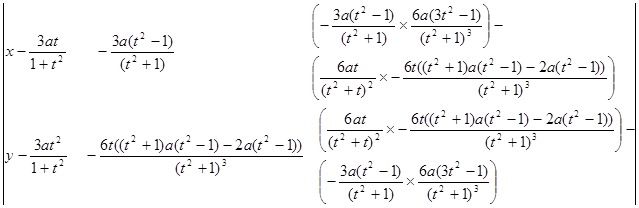
8.     Кривизна:

 

 

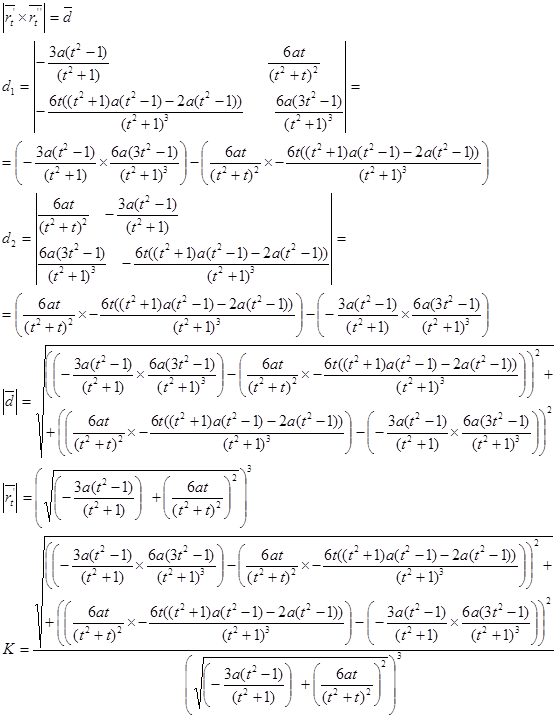
Задание 7. Локон Аньези.

1.     Определим параметризацию:

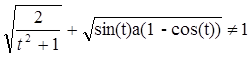
Линия задана в произвольной параметризации.

2.     Найдем производные до третьего порядка включительно:

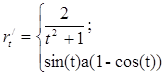
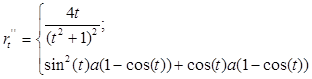
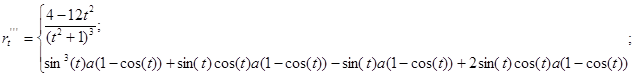
3.     Уравнение касательной:

4.     Уравнение нормали:

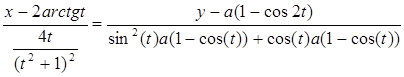
5.     Уравнение бинормали:

6.     Уравнение соприкасающейся плоскости:

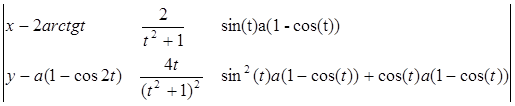
7.     Спрямляющая плоскость:

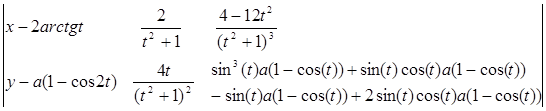
8.     Кривизна:

 

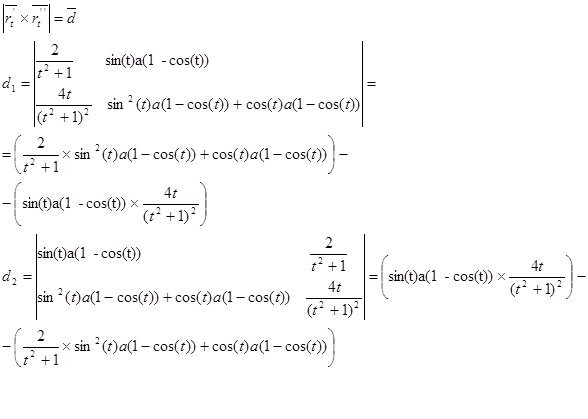
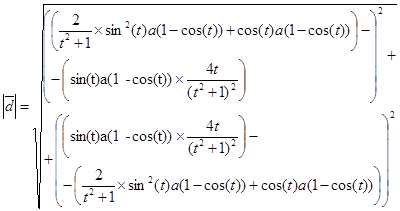
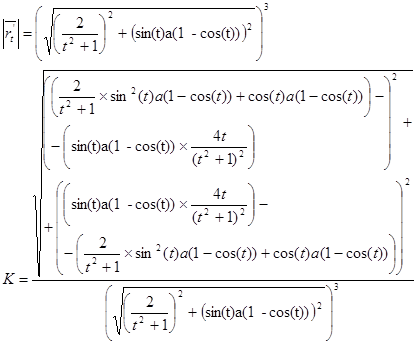
Задание 8. Строфоида.

1.     Определим параметризацию:

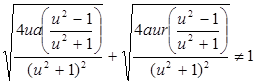
Линия задана в произвольной параметризации.

2.     Найдем производные до третьего порядка включительно:

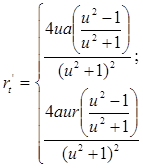
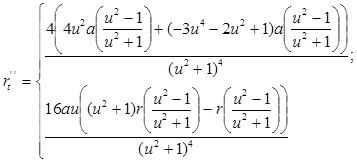
3.     Уравнение касательной:

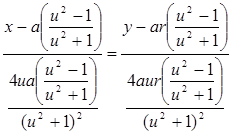
4.     Уравнение нормали:

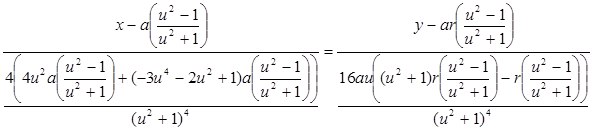
5.     Уравнение бинормали:

6.     Уравнение соприкасающейся плоскости:

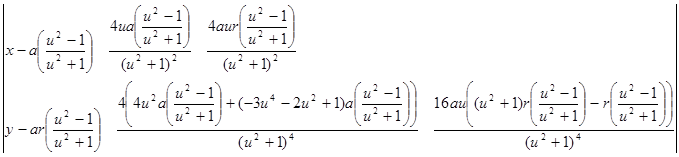
7.     Спрямляющая плоскость:

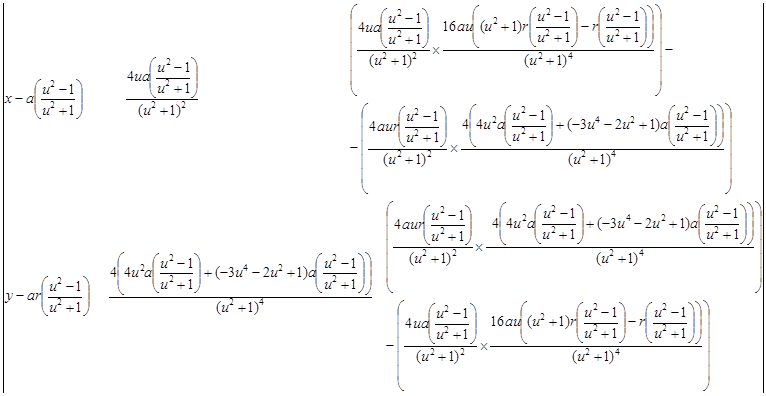
8.     Кривизна:

 

 

 

 

Заключение

 

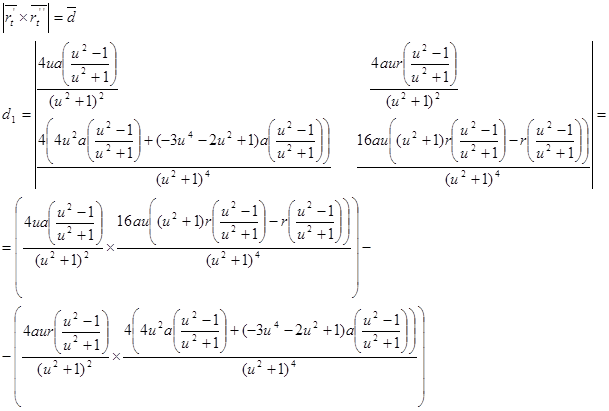
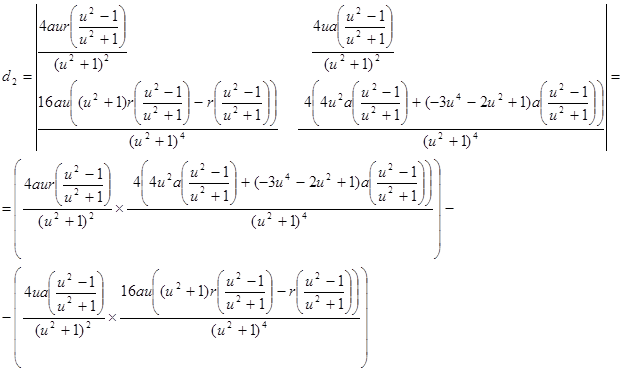
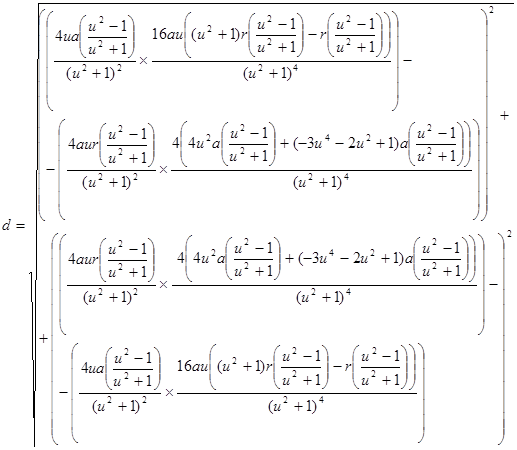
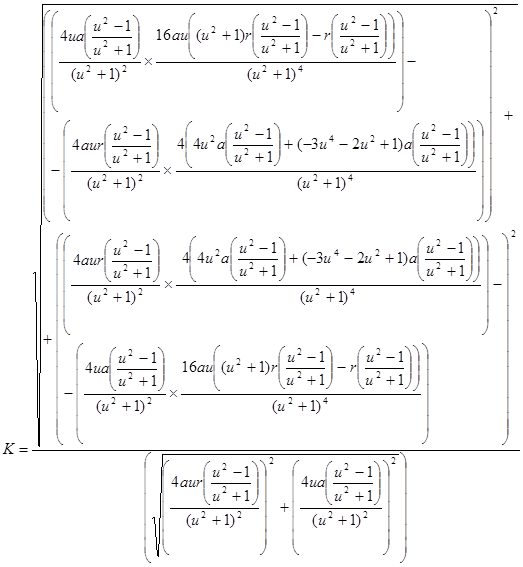
В данной работе мы рассмотрели некоторые замечательные кривые третьего порядка, изучили их способы построения, особенности формы и задачи, связанные с этими кривыми.

В главе 1 было рассмотрено понятие кривой третьего порядка, свойства кубик и классификация Ньютона кривых третьего порядка. Ньютон делит все кривые 3-го порядка на 7 классов, 14 родов, 72 типа.

Во 2-й главе мы изучили частные случаи кривых третьего порядка:

·                   Декартов лист

·                   Циссоида Диоклеса

·                   Локон Аньези

·                   Строфоида

В главе 3 рассмотрели задачи на использование методов дифференциальной геометрии для исследования линий третьего порядка.

Были определены особые точки, асимптоты и построены линии третьего порядка.

В ходе рассматривания кривых третьего порядка мы познакомились с некоторыми поистине замечательными кривыми, населяющими удивительный мир аналитической геометрии, которые встречаются в нашей жизни гораздо чаще, чем кажется. В данной работе собрали материал с уклоном на практическое построение кривых.

 

 

Список литературы

 

1.                 Атанасян Л.С. и Атанасян В.А., Сборник задач по геометрии. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. Ч. I, М., "Просвещение", 1973, 256 с.

2.                 Выгодский М.Я., Справочник по высшей математике, М.: АСТ: Астрель, 2008, 991 с. с ил.

3.                 Гурова А.Э. Замечательные кривые вокруг нас. М, 1989

4.                 Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1971. – 232 с.

5.                 История математики с древнейших времен до начала XIX столетия/ Под ред. А.П. Юшкевича. – М.: Наука, 1970, т. 1. – 352 с.; 1970,
т. 2. – 300 с.; 1972, т. 3 – 496 с.

6.                 Коротецкая В.А. Полярная система координат. Магнитогорск, МГМА, 1996.

7.                 Кривые // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб.: 1890—1907.

8.                 Маркушевич А.И. Замечательные кривые. - М, 1978

9.                 Никифоровский В. А., Фрейман Л. С. Рождение новой математики. – М.: Наука, 1976. – 198 с.

10.            Погорелов А. В. Дифференциальная геометрия. - 6-е изд., стереотип. - М., Наука, 1974. - 176 с.

11.                      Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия: первое знакомство. - М.: Изд-во МГУ, 1990. 384 с.

12.            Савелов А. А. Плоские кривые. М., 1960.

13.            Тайманов И. А. Лекции по дифференциальной геометрии. — Ижевск: Институт компьютерных исследований, 2002. - 176 стр.

14.            Тышкевич Р.И., Феденко А.С. Линейная алгебра и аналитическая геометрия. – 2-е изд. – Минск: Выш. Шк., 1976. 544с.

 

15.            Скачано с www.znanio.ru