Круглый стол. Разработка проекта: Рекомендации по оформлению решений заданий по математике

 

Администрация  города Нижнего Новгорода

Департамент образования

Муниципальное  бюджетное общеобразовательное  учреждение

«Школа № 130»

ул. Краснодонцев 1а, г. Нижний Новгород, 603101, тел/факс (831) 293-42-30, e-mail: school130@inbox.ru

 

 

Круглый стол

  учителей математики МБОУ «Школы № 130»

 

Проект «Рекомендации по оформлению решений заданий по математике»

 

Цель: разработать проект «Рекомендации по оформлению решений заданий по математике».

Задачи:

·        обсудить проблематику обозначенного вопроса;

·        рассмотреть предлагаемый проект;

·        принять проект для дальнейших разработок.

Участники: директор ОУ,  заместители директора  ОУ, руководитель ШМО, учителя математики.

Условия и оборудование: кабинет, стулья и столы, компьютер, медиа проектор, компьютерная презентация, доска,  рабочие карточки.

Форма проведения: круглый стол.

 Предварительная подготовка:  участникам заранее сообщается тема, цель, задачи круглого стола, выдаются рабочие карточки с заданиями.

 

Этап 1. Постановка проблемного вопроса

Этап 2. Представление проекта  

Выступление учителя математики Кондаковой Т.Н.

Этап 3. Обсуждение проекта

Директор ОУ,  заместители директора  ОУ, руководитель ШМО, учителя математики

Этап 4. Утверждение проекта «Рекомендации по оформлению решений заданий по математике».

Этап 5. Рефлексия

Этап 6. Подведение итогов.

 

 

 

 

Выступление на заседании ШМО учителя математики Кондаковой Т.Н.

11.01.2019г.

 

Мы сталкиваемся с такой проблемой как не всегда правильное, логически верное оформление  заданий по математике. Ребятам трудно ориентироваться в этом вопросе, так как на разных этапах обучения, начиная с Начальной школы и заканчивая выпускными классами,  происходит смена учительского состава, происходит  замена учебников математики. Каждый учитель считает, что только так,  как он говорит, стоит оформлять задания. Да и с учетом той информации, которую ученики черпают из «просторов» Интернета, например различные сайты, предлагающие доступные решения (ГДЗ), происходят такие разногласия! Поэтому  необходимо выработать единую систему по отработке навыков оформления письменных решений.

Данный проект ориентирован на молодых специалистов, а  также может быть включен в Положение об орфографическом режиме школы.

 

На сегодняшний день нормативных требований к оформлению письменных работ учащихся по математике нет, поэтому я предлагаю обсудить проект «Рекомендации по оформлению письменных работ учащихся по математике».

При составлении данных рекомендаций я учитывала:

а) отсутствие нормативной базы по данному вопросу;
б) рекомендации методистов;
в)  «Единый орфографический режим»;
г) рекомендации по оформлению заданий профильного ЕГЭ по математике.

По данному вопросу я также учла положительные исторические позиции преподавания: письмо Министерства просвещения РСФСР от 16.07.1973 г. № 334-М «О порядке проверки ученических работ в 1–3-х классах общеобразовательных школ»; письмо Министерства просвещения РСФСР от 19.07.1977 г. № 308-М «О письменных работах учащихся общеобразовательных школ»; письмо Министерства просвещения РСФСР от 27.03.1979 г. № 135-М «Об оформлении записей в тетрадях для учащихся начальных классов», методическое письмо Министерства просвещения РСФСР от 01.09.1980 г. № 364-М, Методические рекомендации по оцениванию заданий по математике (ФИПИ).

Воспитание культуры оформления письменных работ является необходимыми, так как:

а) это часть воспитания внутренней культуры учащихся;
б) организация и самоорганизация учащихся для  выполнения письменных работ по математике.

Итак, проект «Рекомендации по оформлению решений заданий по математике» включает в себя следующие пункты:

Общие рекомендации по оформлению решений
Оформление

ü текстовых задач

ü математических выражений

ü решения уравнения

ü решения неравенства

ü решения систем уравнений

ü решения систем неравенств

ü геометрической задачи

 

С общими положениями в проекте, а также с  рекомендациями по оформлению решений текстовых задач, математических выражений и геометрических задач вы можете самостоятельно ознакомиться в Приложении.

Со своей стороны  я хочу остановиться на обосновании  рекомендаций по оформлению уравнений, неравенств и их систем.

 

Согласно ГОСТ 7.32-2001, уравнения, формулы из текста,  выделять необходимо в отдельно взятую строку. Пустая строка ставится как над, так и под каждой из приведённых формул. Когда уравнение не помещается в одну строчку, его нужно перенести после любого математического знака (знак равенства, плюс, минус, умножение, деление и другие) с повторением в начале последующей строки этого знака. Нужно знать, что перенос формулы на знаке умножения сопровождается знаком «х».

УРАВНЕНИЕ — в первоначальном понимании — есть равенство, содержащее одну или несколько переменных (неизвестных).

Считаю, что в школьном курсе математики необходимо избегать употребления в записях таких математических символов, как «стрелки». С осторожностью применять знаки принадлежности и включения.

Для уточнения значений символов предлагаю вашему вниманию следующую таблицу:

Символ	Название	Значение	Пример
	Импликация, следование	А  В обозначает «если {\displaystyle A}А верно, то {\displaystyle B}В также верно».	х=2 х²=4, но х²=4 х=2 - неверно
→	«влечёт» или «если…, то»	может использоваться вместо ⇒ или для обозначения функции,
⇔	Равносильность «если и только если» или «равносильно»	А ⇔ В означает «{\displaystyle A} верно А тогда и только тогда, когда В {\displaystyle B}верно».	Х+5=у+2 ⇔ х+3 = у
	Принадлежность/непринад-лежность к множеству	означает «х{\displaystyle a} является элементом множества {\displaystyle S} А»
⊂	«является подмножеством», «включено в»	обычно означает, что и {\displaystyle A\subseteq B} «каждый элемент из {\displaystyle A}А  также является элементом из {\displaystyle B}В».	N⊂Z

Вам заранее выдавалось задание (Приложение 1). Со своей стороны я вам предлагаю свой взгляд на оформление уравнений, неравенств и их систем.

УРАВНЕНИЯ

1. Употребление символов

   Я считаю, что употребление различных символов - «стрелок» крайне нежелательно. Так как в школьном курсе недостаточно четко объяснено их значение.

2. Второй знак равенства

Второй знак равенства в уравнении – недопустим, так как согласно определению понятия «уравнение»  уравнение – это равенство, состоящее из левой и правой части. Если же ученику необходимо выполнить арифметические расчеты, то вычисления должны быть записаны с правой стороны от уравнения в виде действий или же выполнены устно.

3. Необходимость постановки знака после каждой строчки в уравнении

Я считаю, что постановка орфографического знака «, »  вполне уместна, так как,  

·        во-первых, иногда можно видеть в некоторых изданиях решение уравнения в «строчку», соответственно каждое равенство отделяется «, »,

·        во-вторых, подразумевается, что далее будут продолжаться преобразования данного равенства, т.е. уравнения

·        в-третьих, при постановке «, » учащиеся автоматически не смогут поставить второй знак равенств (см. выше п. 2).

После нахождения  корня  уравнения, перед записью слова «Ответ» необходимо поставить знак «. »  для  того, чтобы показать окончание преобразований. Также  учитывая  правила  русского языка,  новое предложение начинается с большой буквы. Тем более,  слово «Ответ» записывается с большой буквы.

4. Форма записи ответа.

Обратимся к определению корня уравнения. «Корнем уравнения называется значение переменной, при котором уравнение обращается в верное равенство» (Алгебра, 7 класс: учеб. для общеобраз. учреждений [Ю.Н. Макарычев, Н.Г. Миндюк и др.]). Таким образом, решением уравнения является либо число, либо числа, либо устанавливается бесконечное множество корней или их отсутствие..

Соответственно, в «Ответе» должно быть записано число/числа или «бесконечно много корней»/ «корней нет». Поэтому запись в ответе  х= 2 не сочетается с определением «корня уравнения».

Примеры на рисунках:

 

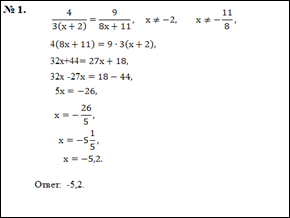
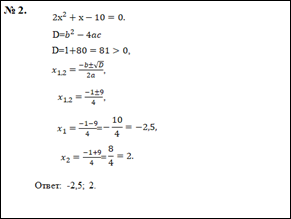
НЕРАВЕНСТВА

При оформлении неравенств,   следует учитывать, что в решении обязательно так называемые, окончательные неравенства, только на основании их записывается ответ в виде промежутка. Еще один довод в обоснование выше сказанного -  так как в дальнейшем с помощью линейных и квадратных неравенств решаются тригонометрические, показательные и логарифмические неравенства путем замены переменной, то возникает необходимость вернуться к замене переменных, а это можно сделать только в случае,  если решение неравенства в новых переменных  записано в виде неравенства.

    Запись ответа неравенства предпочтительна в виде промежутка или  

    объединения промежутков, но допустима  и в виде неравенства или объединения   

    неравенств. Причем запись «» не допустима, так как присутствует логическая ошибка.

В качестве примера рассмотрю методы решения квадратного неравенства

Возможно три способа:

I. Метод интервалов.

II. Метод через параболу.

III. Метод по правилу.

 

Стоит объяснить ученикам преимущества и недостатки каждого метода.

Рассмотрим

1. Метод интервалов.

Его стоит применять, если в левой части неравенства – произведение скобок, в которых переменная в первой степени, а в правой части – ноль. Пример оформления представлен на рисунке:

2. Метод через параболу.

В левой части - квадратный трёхчлен, в правой – ноль. Пример оформления представлен на рисунке:

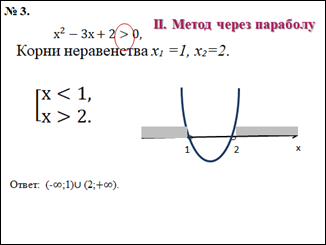
3. Метод по правилу.

Чаще всего этот метод применяется при произведении двух функций. При решении квадратных неравенств ученики допускают ошибки при оформлении, которые приводят к логическим ошибкам, а,  следовательно,  к неправильному ответу. Пример правильного оформления представлен на рисунке:

СИСТЕМЫ УРАВНЕНИЙ

Система уравнений оформляется  как и уравнения, но после записи последнего уравнения стоит поставить «;» . При записи последней системы в конце ставить «.». Тем самым, мы понимаем, что решение закончено и далее следует «Ответ».

Ответ системы двух уравнений записывается в виде координат точки, если переменные «х» и «у». Это следует из графического представления системы двух уравнений с двумя неизвестными – пересечения графиков двух функций. Если же переменные записаны другими буквами, то оформление в виде круглых скобок и буквы в алфавитном порядке. Но допускается запись в ответе и равенств через запятую. Но я хочу остановиться на моменте, когда необходимо выйти из системы и решить отдельно одно из уравнений. Я считаю, что надо обязательно сделать запись «решим/решу первое/второе уравнение системы», а затем обязательно вернуться к системе. Примеры на рисунках:

 

СИСТЕМЫ  НЕРАВЕНС ТВ

Оформление аналогично системе уравнений, но стоит обратить внимание на последнюю систему. Если стоит фигурная скобка, то считается, что система не решена, обязательно надо найти пересечение решений неравенств из системы и записать «окончательное» неравенство или совокупность неравенств. Повторюсь, что это необходимо, так как в дальнейшем с помощью линейных и квадратных неравенств решаются тригонометрические, показательные и логарифмические неравенства путем замены переменной. Пример на рисунке:

 

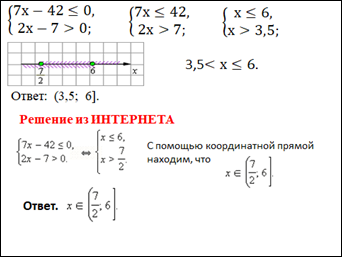
Думаю, что я дала наиболее полное обоснование для рекомендаций по оформлению уравнений, неравенств и их систем. Принять к сведению информацию или нет – это ваше право. Но мы все убеждены, что учитель математики не только дает знания по своему предмету, но и воспитывает  детей, учит быть грамотными и точными, как сама наша любимая наука – МАТЕМАТИКА. Спасибо за внимание.

 

Интернет-ресурсы

1.      http://fipi.ru/documents?field_yesar_tid=20602&term_node_tid_depth=18&field_discipline_tid=24

2.      http://fipi.ru/documents?field_yesar_tid=20602&term_node_tid_depth=20606&field_discipline_tid=24

3.      https://megaresheba.ru/publ/reshebnik/algebra/9_klass_alimov/34-1-0-1965#task?t=20-nomer

4.      https://alleng.org/d/math/math2237.htm

5.      http://www.xn-----8kcodrdcygecwgg0byh.xn--p1ai/pravila-oformleniia-diplomnoi-raboty#formuly

6.      https://ru.wikipedia.org/wiki/%D0%A2%D0%B0%D0%B1%D0%BB%D0%B8%D1%86%D0%B0_%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D1%85_%D1%81%D0%B8%D0%BC%D0%B2%D0%BE%D0%BB%D0%BE%D0%B2

7.      http://edu.sernam.ru/book_kiber1.php?id=99

8.      http://su-school4.ucoz.ru/Documentation/Pamatki/oformlenie_pismennykh_rabot_uchashhikhsja.pdf

9.      https://www.google.com/search?q=%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8+%D0%BC%D0%BE%D0%BB%D0%BE%D0%B4%D0%BE%D0%B3%D0%BE+%D1%83%D1%87%D0%B8%D1%82%D0%B5%D0%BB%D1%8F&tbm=isch&tbo=u&source=univ&sa=X&ved=2ahUKEwi13JfbmeTfAhWOxYsKHXkfD0wQsAR6BAgGEAE&biw=1350&bih=638#imgrc=VGEVfnKjFmck2M:

10.  https://www.google.com/search?q=%D0%BA%D0%B0%D1%80%D1%82%D0%B8%D0%BD%D0%BA%D0%B8+%D0%BC%D0%BE%D0%BB%D0%BE%D0%B4%D0%BE%D0%B3%D0%BE+%D1%83%D1%87%D0%B8%D1%82%D0%B5%D0%BB%D1%8F&tbm=isch&tbo=u&source=univ&sa=X&ved=2ahUKEwi13JfbmeTfAhWOxYsKHXkfD0wQsAR6BAgGEAE&biw=1350&bih=638#imgdii=TykAoIMoHKDRAM:&imgrc=VGEVfnKjFmck2M:

11.  https://mathematics.ru/courses/algebra/content/chapter3/section3/paragraph5/theory.html#.XDfIAVUzbIU

12.  https://www.google.com/search?q=gif+%D0%B0%D0%BD%D0%B8%D0%BC%D0%B0%D1%86%D0%B8%D1%8F+%D0%BC%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D0%BA%D0%B0&tbm=isch&tbo=u&source=univ&sa=X&ved=2ahUKEwj-vNC5peTfAhVF_ywKHfjxCyIQsAR6BAgFEAE&biw=1350&bih=638#imgdii=tkVT_eBZj6GLQM:&imgrc=vH5qLjHT0ho0mM:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 1.

Уважаемые коллеги! Для проведения  круглого стола  учителей математики ШМО, обсуждения  проекта  «Рекомендации по оформлению решений заданий по математике» выполните, пожалуйста, задания с  полным оформлением. СПАСИБО

 

№ 1. Решите уравнение  .

№ 2. Решите уравнение  

№ 3. Решите неравенство: .

 

№ 4. Решите систему уравнений:

№ 5. Решите систему уравнений:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Приложение 2.

Проект

«Рекомендации

по оформлению решений заданий по математике»

Общие положения

- после записи номера задания  вниз отступается одна клетка;
- выполняется краткая запись в виде рисунка, таблицы, чертежа и т.д.;
- запись слов, числовых значений, стрелки, фигурные скобки производится синей пастой, чертежи  выполняются только простым карандашом;
- решение задачи записывается ниже с отступом одной клетки от краткой записи; 
- каждое действие задачи записывается с отступом одной клетки с указанием порядка действия;
- запись наименований полученного результата обязательна в скобках после каждого действия;

- запись наименования производится сокращенно;

- запись сокращается по последней согласной букве; 
- к каждому действию, кроме последнего, записывается пояснение;

- ответ записывается полный с отступом одной клетки от решения;

- принятые международные сокращения,  такие как: кг, дм, см, га, м, дм, мм и т.д.  в ответе записываются кратко, после сокращений точка не ставится.

Оформление текстовых задач:

·              Краткая запись задачи выполняется по усмотрению учителя в любой удобной для этого форме: таблица, схема, словесная краткая запись и пр.

·              Решение задачи записывается по действиям или выражением с пропуском одной клетки между действиями.

·              Запись наименований обязательна, запись пояснений делается кратко, по усмотрению учителя.

·              Ответ к задаче записывается, начиная с числительного.

·              Принятые сокращения, такие как: см, кг, м и т.д. в ответе записываются кратко.

 

Оформление математических выражений и равенств:

·              Расстояние между выражениями вниз составляет 2 клетки.

·              Между столбиками выражений, неравенств, уравнений делаем отступ вправо на 4 клетки (пишем на пятой).

·              При вычислении выражений с несколькими математическими действиями их порядок фиксируется над знаком простым карандашом. Затем решение расписывается полностью под выражением с фиксацией конечного результата в записи выражения.

 

Оформление решения уравнения:

·              Решение уравнения записывается в столбик.

·              Вычисления проводятся справа на свободных клетках.

·              Знак равенства записывается в каждой строчке только один раз.

·              После каждой строчки ставить знак «,».

·              В последней строчке ставить знак «.».

·              Проверка найденного значения неизвестного проводится письменно или устно.

·              Обязательна запись слова «Ответ» с заглавной буквы.

·              В ответе записывается число/числа/ или вывод бесконечно много решений/решений нет.

 

Оформление систем уравнений

·              Решение систем уравнений записывается в столбик или в строчку.

·              Знак равенства записывается в каждой строчке только один раз.

·              После первой строчки системы ставить знак «,», после последнего уравнения в системе ставить знак «;».

·              В последней строчке в последнем уравнении ставить знак «.».

·              Проверка найденного значения неизвестного проводится письменно или устно.

·              Обязательна запись слова «Ответ» с заглавной буквы.

·              Ответ записывается в виде координат точки (в круглых скобках) или делается вывод «бесконечно много решений/решений нет».

·              При необходимости отдельного решения уравнения системы следует сделать запись «Решим первое/второе уравнение системы». Далее приводится решение уравнения, затем делается запись «Вернемся к системе уравнений».

 

Оформление решения неравенства:

·              Решение неравенства записывается в столбик.

·              Вычисления проводятся справа на свободных клетках.

·              Знак неравенства (кроме двойного неравенства) записывается в каждой строчке только один раз.

·              После каждой строчки ставить знак «,».

·              В последней строчке ставить знак «.».

·              На основании последнего неравенства записывается ответ.

·              Обязательна запись слова «Ответ» с заглавной буквы.

·              Ответ записывается в виде промежутка или вывод «бесконечно много решений/решений нет».  Допускается в ответе запись последнего неравенства.

 

Оформление решения систем неравенств:

·              Решение систем неравенств записывается в столбик или в строчку.

·              Вычисления проводятся справа на свободных клетках.

·              Знак неравенства (кроме двойных неравенств) записывается в каждой строчке только один раз.

·              После первой строчки системы ставить знак «,», после последнего неравенства в системе ставить знак «;».

·              В последней строчке ставить знак «.».

·              Система неравенств является решенной, если записано последнее неравенство/совокупность неравенств.

·              На основании последнего неравенства/совокупности неравенств записывается ответ.

·              Обязательна запись слова «Ответ» с заглавной буквы.

·              Ответ записывается в виде промежутка/объединения промежутков или вывод «бесконечно много решений/решений нет». Допускается в ответе запись последних неравенств.

 

Оформление геометрической задачи:

·               Краткая запись делается исходя из  условия задачи  (Дано:… ).

·              Чертёж при необходимости выполняется справа простым карандашом при помощи геометрических инструментов по имеющимся данным или в пропорции. Буквенное «имя» фигуры записывается заглавными буквами латинского алфавита, начиная с левого нижнего угла по часовой стрелке.

·           Запись вопроса задачи начинать со слова  «Найти: Р.», причем далее вопросительный знак не ставиться.

·              Далее записывается слово «Решение». В решении сначала записывается формула, затем в неё подставляются числовые данные. Если в ходе необходимо провести предварительные вычисления, то запись выполняется по действиям, как в текстовой задаче. Текстовые пояснения к действиям не выполняются - они содержатся в начале записи.

·              Ответ в геометрической задаче записывается кратко с помощью символов.

 

 

 

 

 

 

 

 

«Образованный человек тем и                                  отличается от   необразованного,                                  что продолжает считать свое                                  образование незаконченным».                                                                        К. Симонов

Администрация  города Нижнего Новгорода Департамент образования Муниципальное  бюджетное общеобразовательное  учреждение «Школа № 130» ул. Краснодонцев 1а, г. Нижний Новгород, 603101, тел/факс (831) 293-42-30, e-mail: school130@inbox.ru                                         Нижний Новгород, 11 января 2019 г.       Круглый стол  учителей математики МБОУ «Школы № 130»   Проект         Цель: разработать проект «Рекомендации по оформлению решений заданий по математике». Задачи: ·        обсудить проблематику обозначенного вопроса; ·        рассмотреть предлагаемый проект; ·        принять проект.   Этап 1. Постановка проблемного вопроса Этап 2. Представление проекта  Выступление учителя математики Кондаковой Т.Н. Этап 3. Обсуждение проекта Директор ОУ,  заместители директора ОУ, руководитель ШМО, учителя математики Этап 4. Утверждение проекта «Рекомендации по оформлению решений заданий по математике» Этап 5. Рефлексия Этап 6. Подведение итогов

 

 

Скачано с www.znanio.ru