ЛАБОРАТОРНАЯ РАБОТА № 2. «РЕШЕНИЕ ДВУХИНДЕКСНЫХ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

ЛАБОРАТОРНАЯ РАБОТА № 2. «РЕШЕНИЕ ДВУХИНДЕКСНЫХ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

С ИСПОЛЬЗОВАНИЕМ Microsoft Excel. ТРАНСПОРТНАЯ ЗАДАЧА»

 

2.1 ЦЕЛЬ РАБОТЫ

 

Приобретение навыков построения математических моделей стандартных транспортных задач ЛП и решения их в Microsoft Excel.

 

2.2 ОСНОВНЫЕ ПОЛОЖЕНИЯ

 

Задача о размещении (транспортная задача) – это распределительная задача, в которой работы и ресурсы измеряются в одних и тех же единицах. В таких задачах ресурсы могут быть разделены между работами, и отдельные работы могут быть выполнены с помощью различных комбинаций ресурсов. Примером типичной транспортной задачи является распределение (транспортировка) продукции, находящейся на складах, по предприятиям-потребителям.

Стандартная ТЗ определяется как задача разработки наиболее экономичного плана перевозки продукции одного вида из нескольких пунктов отправления в пункты назначения. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

 

Исходные параметры модели ТЗ

 

a) n – количество пунктов отправления, m – количество пунктов назначения;

b)  – запас продукции в пункте отправления  () (ед. тов.);

c)  – спрос на продукцию в пункте назначения  () (ед. тов.);

d)  – тариф (стоимость) перевозки единицы продукции из пункта отправления  в пункт назначения  (руб./ед. тов.).

 

Искомые параметры модели ТЗ

 

1  – количество продукции, перевозимой из пункта отправления  в пункт назначения  (ед. тов.).

2  – транспортные расходы на перевозку всей продукции (руб.).

 

Этапы построения модели

Определение переменных.

Проверка сбалансированности задачи.

Построение сбалансированной транспортной матрицы.

Задание ЦФ.

Задание ограничений.

 

Транспортная модель

 

 

Целевая функция представляет собой транспортные расходы на осуществление всех перевозок в целом. Первая группа ограничений указывает, что запас продукции в любом пункте отправления должен быть равен суммарному объему перевозок продукции из этого пункта. Вторая группа ограничений указывает, что суммарные перевозки продукции в некоторый пункт потребления должны полностью удовлетворить спрос на продукцию в этом пункте. Наглядной формой представления модели ТЗ является транспортная матрица (табл. 2.1).

 

Таблица 2.1

 

Общий вид транспортной матрицы

 

 

Из модели (2.1) следует, что сумма запасов продукции во всех пунктах отправления должна равняться суммарной потребности во всех пунктах потребления, то есть

 

 

Если (2.2) выполняется, то ТЗ называется сбалансированной, в противном случае – несбалансированной. Поскольку ограничения модели (2.1) могут быть выполнены только при сбалансированной ТЗ, то при построении транспортной модели необходимо проверять условие баланса (2.2). В случае, когда суммарные запасы превышают суммарные потребности, необходим дополнительный фиктивный пункт потребления, который будет формально потреблять существующий излишек запасов, то есть

 

 

Если суммарные потребности превышают суммарные запасы, то необходим дополнительный фиктивный пункт отправления, формально восполняющий существующий недостаток продукции в пунктах отправления:

 

 

Введение фиктивного потребителя или отправителя повлечет необходимость формального задания фиктивных тарифов  (реально не существующих) для фиктивных перевозок.

Поскольку нас интересует определение наиболее выгодных реальных перевозок, то необходимо предусмотреть, чтобы при решении задачи (при нахождении опорных планов) фиктивные перевозки не рассматривались до тех пор, пока не будут определены все реальные перевозки. Для этого надо фиктивные перевозки сделать невыгодными, то есть дорогими, чтобы при поиске решения задачи их рассматривали в самую последнюю очередь. Таким образом, величина фиктивных тарифов должна превышать максимальный из реальных тарифов, используемых в модели, то есть

 

.

 

На практике возможны ситуации, когда в определенных направлениях перевозки продукции невозможны, например, по причине ремонта транспортных магистралей. Такие ситуации моделируются с помощью введения так называемых запрещающих тарифов . Запрещающие тарифы должны сделать невозможными, то есть совершенно невыгодными, перевозки в соответствующих направлениях. Для этого величина запрещающих тарифов должна превышать максимальный из реальных тарифов, используемых в модели:

 

.

 

2.3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

 

1 Согласно номеру своего варианта выберите условие задачи.

2 Постройте модель задачи, включая транспортную таблицу.

3 Найдите оптимальное решение задачи в Excel и продемонстрируйте его преподавателю.

4 Оформите отчет по лабораторной работе.

Двухиндексные задачи ЛП вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.

Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара от поставщиков потребителям (табл. 2.2).

 

Таблица 2.2

 

Исходные данные транспортной задачи

 

 

Целевая функция и ограничения данной задачи имеют вид

 

 

Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (2.5) и ее решение представлены на рис. 2.1, 2.2, 2.3 и в табл. 2.3.

 

 

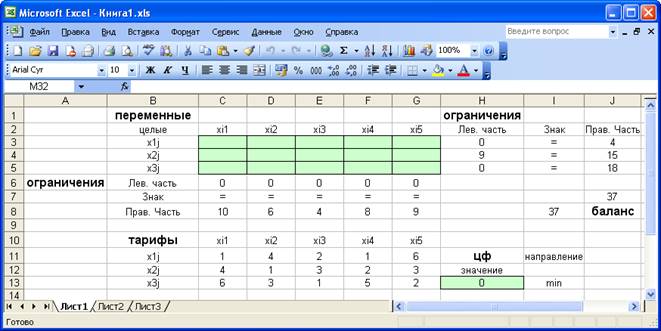
Рис. 2.1. Экранная форма двухиндексной задачи (2.5)

(курсор в целевой ячейке Н13)

 

Таблица 2.3

 

Формулы экранной формы задачи (2.5)

 

 

 

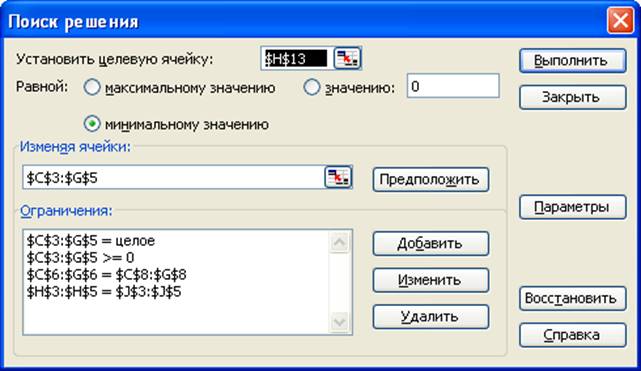
Рис. 2.2. Ограничения и граничные условия задачи (2.5)

 

 

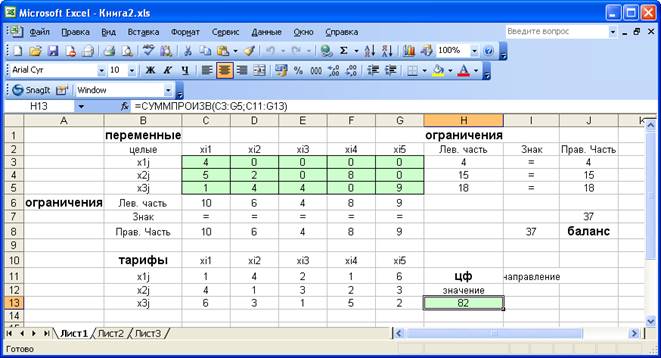
Рис. 2.3. Экранная форма после получения решения задачи (2.5)

(курсор в целевой ячейке H13)

 

2.4 СОДЕРЖАНИЕ ОТЧЕТА

 

Отчет должен содержать:

·                                           титульный лист (см. рис. 2.1);

·                                           номер варианта

·                                           транспортную таблицу и модель задачи в Microsoft Excel с указанием всех единиц измерения;

·                                           результаты решения задачи с указанием единиц измерения.

Обязательно наличие выводов по проделанной работе. В случае несвоевременного выполнения задания к отчету прилагается дискета с выполненным заданием.

 

2.5 КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1 Что такое задача о размещении?

2 Какова постановка стандартной ТЗ?

3 Запишите математическую модель ТЗ.

4 Перечислите исходные и искомые параметры модели ТЗ.

5 Какова суть каждого из этапов построения модели ТЗ?

6 Раскройте понятие сбалансированности ТЗ.

7 Что такое фиктивные тарифы?

 

2.6 ЗАДАНИЯ

 

Используя MS Excel, найти решение ТЗ, соответствующей заданному варианту (табл. 2.4).

Таблица 2.4

 

 

Скачано с www.znanio.ru