Лабораторная работа

ОПРЕДЕЛЕНИЕ МОДУЛЯ ЮНГА

Цель работы: определить модуль Юнга стали, оценить погрешность измерений.

Приборы и материалы: резиновый шнур, закрепленный на кронштейне; грузы для растяжения, микрометр или штангенциркуль, линейка.

Краткая теория

Все твердые тела под действием сил деформируются, т.е. изменяют объем и форму. Различаются деформации растяжения (сжатия), сдвига, изгиба, кручения.

Если деформации исчезают после прекращения действия приложенных сил, то они называются упругими. Деформации, частично сохраняющиеся после снятия нагрузки, называются пластическими. Разделение деформаций на упругие и пластические условно. Строго говоря, после любой нагрузки, сохраняются остаточные деформации. Но если они пренебрежимо малы, то деформации считаются упругими.

Рассмотрим деформацию растяжения на примере одного изотропного образца, например, проволоки. Пусть верхний конец проволоки закреплен, а к нижнему подвешиваются различные грузы . В качестве меры деформации растяжения используют абсолютное удлинение  или относительное удлинение , где  – начальная длина проволоки, а  – ее длина при нагрузке. Относительное удлинение  рассчитывается на единицу начальной длины и поэтому, в отличие от абсолютного удлинения , от длины проволоки не зависит.

Величина

                                                                                                    (1)

определяет упругую силу, действующую на единицу площадки, перпендикулярной направлению силы. Она называется напряжением.

В пределах упругих деформаций напряжение прямо пропорционально относительному удлинению (закон Гука для деформации растяжения):

                                                     ,                                                (2)

где  - коэффициент пропорциональности, называемый модулем упругости (модулем Юнга) материала образца. Модуль упругости численно равен напряжению, которое возникло бы в теле при его относительном удлинении, равном единице, если бы деформация оставалась упругой.

Зависимость напряжения  от относительного удлинения  изображена на рисунке 1. При малых деформациях (от 0 до ) выполняется закон Гука; это практически линейный участок 0a . Максимальное напряжение , соответствующее этому участку, называется пределом пропорциональности. Предел упругости  - это максимальное напряжение, при котором еще сохраняются упругие свойства тела. На участке ab деформация нелинейная, но еще упругая (обычно этот участок очень малый:  больше  на доли процента.) При напряжениях, больших , деформация становится пластической: в теле после снятия нагрузки наблюдается остаточная деформация . При напряжениях  удлинение нарастает практически без увеличения нагрузки. Это область текучести материала (участок cd). На участке de происходит некоторое упрочение образца. После достижения максимального значения  – предела прочности – напряжение резко уменьшается, и образец разрушается (точка f на графике).

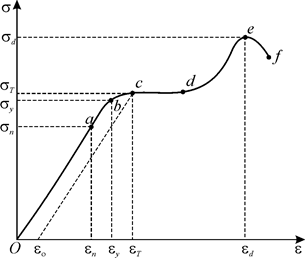
Рис. 1. Зависимость нормального напряжения  
от относительного удлинения

Описание установки

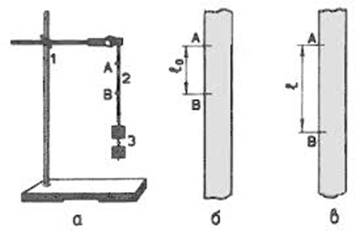
Рис.2. Описание установки по определению модуля Юнга

Модуль Юнга вычисляется по формуле полученной из закона Гука:

                                          (3)

где Е - модуль Юнга; F - сила упругости, возникающая в растянутом шнуре и равная весу прикрепленных к шнуру грузов F = P = m*g; S - площадь поперечного сечения деформированного шнура; l₀ - расстояние между метками А и В на не растянутом шнуре (рис. б); l - расстояние между этими же метками на растянутом шнуре (рис. в). Если поперечное сечение имеет форму круга, то площадь сечения выражается через диаметр шнура:

                                          (4)

Окончательная формула для определения модуля Юнга имеет

вид:

                                      (5)

Выполнение работы

1.     Прикрепите отрезок резинового шнура к штативу одним из концов. Измерьте его диаметр и запишите в таблицу.

2.     Поставьте на нем произвольно две отметки А и В на расстоянии не менее 10 см друг от друга. Измерьте и занесите измеренное значение в таблицу.

3.     Подвесьте на свободный конец шнура груз известной массы m и измерьте новое расстояние между точками А и В.

4.     Результаты измерений занесите в таблицу 1.

5.     Вычислите модуль упругости резины по формуле (5).

6.     Определите абсолютные погрешности измеряемых величин.

7.     Вычислите относительную погрешность модуля упругости по формуле

8.     Рассчитайте абсолютную погрешность: .

9.     Запишите ответ в виде:

10. Сравните полученные данные с табличными и сделайте вывод, ответив на контрольные вопросы.

Таблица 1.

Результаты измерений и расчетов для определения модуля упругости.

Контрольные вопросы

1.     Сформулируйте закон Гука для изучаемых деформаций. Исходя из каких соображений подбираются внешние нагрузки для проверки закона Гука?

2.     Каков физический смысл модуля Юнга? От чего зависит эта величина?

3.     Опишите зависимость  от  при растяжении стержня.