Поделиться
ск-17 1 лаб тт (2).docx
Лабораторная работа №1
Тема: Исследование характеристик потоков вызовов
Задачи:
1) Рассчитать время доставки пакетов в сети с установлением соединения и без установления соединения.
2) Построить кривые распределения вероятностей Pi и произвести сравнение полученных результатов.
Цель работы:
1) Расчёт времени доставки пакетов в сети с установлением соединения и без установления соединения. Моделирование самоподобных случайных процессов. Анализ систем с самоподобным характером времени обслуживания.
На коммутационную систему поступает поток
вызовов, создающий нагрузку Y
Эрл. Определить вероятности поступления i
вызовов
при примитивном потоке
от N источников
и 
при простейшем потоке
вызовов. Построить кривые распределения вероятностей 
и произвести сравнение полученных
результатов.
Дано:
Y = 2,3 Эрл
N = 6
Решение:
Поток примитивный– это поток от ограниченного числа источников.
Математической моделью простейшего потока является формула Пуассона:
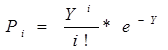
Pi– вероятность поступления i-вызовов
Pi– число вызовов i = (0,…….6)
Остальные значения вычисляем по рекуррентным формулам:
P1 =P0 * Y = 0,1*2,3 =0,23
P2= P1* Y/2 = 0,23 * 2,3/2 = 0.2645
P3 = P2 * Y/3 = 0,2645 * 2,3/3 = 0,2028
P4 = P3 * Y/4 = 0,2028 * 2,3/4 = 0,117
P5 = P4 * Y/5 = 0,117 * 2,3/5 = 0,054
P6 = P5 * Y/6 = 0,054 * 2,3/6 = 0,02
При определении вероятности поступления
вызовов примитивного потока используем распределения Бернулли.
- удельная нагрузка, поступающая от одного
источника:
a = Y/N = 2,3/7 = 0,32 Эрл
P0 = 
Остальные вероятности определяются по рекурентным формулам:
К=0 
К=1 
К=2 
К=3 
К=4 
К=5 
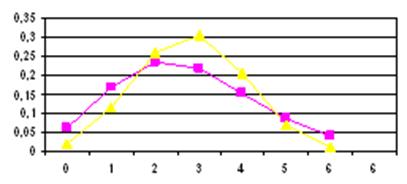
Построим
график
Вывод: Чем меньше число источников вызовов, тем выше вероятность поступления среднего числа вызовов.
Приложение
Таблица вариантов на лабораторную работу №1
|
№ |
Y |
|
1 |
1,3 |
|
2 |
1,5 |
|
3 |
1,7 |
|
4 |
1,9 |
|
5 |
2,1 |
|
6 |
2,3 |
|
7 |
2,5 |
|
8 |
2,7 |
|
9 |
2,9 |
|
10 |
3,1 |
|
11 |
3,2 |
|
12 |
3,3 |
|
13 |
3,4 |
|
14 |
3,5 |
|
15 |
3,6 |
|
16 |
3,7 |
|
17 |
3,8 |
|
18 |
3,9 |
|
19 |
4,0 |
|
20 |
4,1 |
|
21 |
4,2 |
|
22 |
4,3 |
|
23 |
4,4 |
|
24 |
4,5 |
|
25 |
4,6 |
|
26 |
4,7 |
|
27 |
4,8 |
|
28 |
4,9 |
|
29 |
5,0 |
|
30 |
5,1 |
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
