Лабораторная работа №2. Линейный алгоритм вычисление по математическим и физическим формулам

Лабораторная работа №2. Линейный алгоритм вычисление по математическим и физическим формулам

Пример:

Рассчитать площадь прямоугольника по известным его сторонам.

Выполнение:

1 Требования к заголовку пользовательской формы аналогичны требованиям предыдущего задания.

2 Сама форма должна содержать надпись Label1 и кнопку CommandButton1 с соответствующим заголовком (рис. 12). Ввод чисел будет производиться в окне ввода InputBox, вызываемом в теле процедуры.

Рис. 12. Окно формы для примера лабораторной работы № 2

3 Подпрограмма расчета площади прямоугольника имеет следующий вид:

Private Sub CommandButton1_Click()

Dim A As Single, B As Single, S As Single

A = InputBox("Введите одну сторону прямоугольника")

B = InputBox("Введите вторую сторону прямоугольника")

S = A * B

MsgBox "Площадь равна" & S

End Sub

4 Выполните задание своего варианта (номер варианта совпадает с номером студента в журнале).

5 В окне документа Microsoft Office Word оформите лист отчета, соответствующий второму заданию («Линейный алгоритм: вычисление по математическим и физическим формулам») по образцу, приведенному в Приложении 1.

Варианты

1 Даны действительные числа А, В, С. По трем сторонам с длинами А, В, С можно построить треугольник. Найти пеpиметp треугольника.

2 Найти площадь сектора, радиус которого равен R, а дуга содержит заданное число радиан F.

.

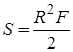3 Первый член возрастающей геометрической прогрессии a₁ = 3, ее знаменатель  q = 2. Найти сумму членов этой прогрессии с 20-го по 25-й.

.

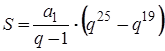4 Дана длина ребра куба. Найти объем куба и площадь его поверхности.

.

5 Даны два действительных положительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел.

.

6 Дан радиус шара. Найти его объем.

.

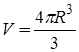7 Определить периметр правильного шестиугольника, описанного окружностью радиуса R.

.

8 Три сопротивления R1, R2, R3 соединены параллельно. Найти сопротивление соединения.

.

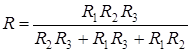9 Определить время падения камня с высоты H.

 ;  .

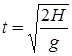10 Дана сторона равностороннего треугольника. Найти площадь этого треугольника.

.

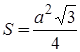11 Рассчитать, какую массу соли и воды надо взять для приготовления раствора массой m грамм с массовой долей соли w %.

соль: ;                      вода: .

12 Опредeлить высоту треугольника, если его площадь равна S, а основание больше высоты на величину А.

.

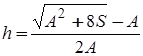13 Три сопротивления R1, R2, R3 соединены последовательно. Найти сопротивление соединения.

.

14 Определить силу притяжения F между телами массы М1 и М2, находящимися на расстоянии Р друг от друга.

.

15 Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус oписанной окружности.

.

16 Даны два действительных числа. Найти среднее арифметическое и среднее геометрическое их модулей.

.

17 Известна длина окружности. Найти площадь круга, ограниченного этой  окружностью.

.

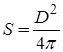18 Найти площадь кольца, внутренний радиус которого равен 20, а внешний – заданному числу R (R > 20).

.

19 Треугольник является pавностоpонним. Известен радиус описанной окружности. Найти стороны треугольника.

.

20 Определить периметр правильного четырехугольника, описанного окружностью радиуса R.

.

21 Даны действительные числа А и В. Получить z = arctg(ab)+cos(b).

22 Вычислить координаты центра тяжести трех материальных точек с массами М1, М2, М3 и координатами (х1, y1), (x2, y2), (x3, y3).

  ;      .

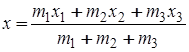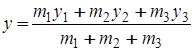23 Квадpат задан длиной стороны. Найти радиусы вписанной и описанной окружностей.

вписанная окружность:  ;  описанная окружность: .

24 Вычислить расстояние между двумя точками с координатами x1, y1 и x2, y2.

.

25 Даны действительные числа А, В, С. По трем сторонам с длинами А, В, С можно построить треугольник. Найти площадь треугольника.

 ,   - полупериметр.

26 Найти длину сектора, радиус которого равен R, а дуга содержит заданное число радиан F.

.

27 Составьте программу, вычисляющую, сколько процентов от (А+В+С) приходится на А, В, С соответственно.

28 Даны действительные числа А и В. Получить z = arcsin (|ab|)+10 sin(b).

.

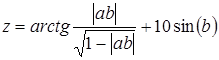29 Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.

30 Даны два целых числа А и В. Получить их частное, остаток от целочисленного деления А на В, а также значение степени числа А^В.