Лабораторная работа №3 Тема: Исследование характеристик потоков вызовов

Лабораторная работа №3

Тема: Исследование характеристик потоков вызовов

Задачи:

1) Расчёт параметров симметричного, примитивного потоков, потоков с повторными вызовами и с ограниченными последействиями. Нахождение характеристик потоков Пальма и Эрланга. Расчёт нагрузок на входах и выходах ступеней искания коммутационных узлов. Расчёт нагрузок, поступающих на регистры и маркеры.

2) Расчёт параметров системы с отказами, с ожиданием, смешанного типа при примитивном потоке вызовов. Расчет потерь для многозвенных схем. Вычисление потерь методом вероятностных графов.

Цели работы:

1) Для заданного блока ГИ методом Якобеуса рассчитать число линий в НПД пучке для направления от АТСК-3 к проектируемой АТСЭ-4 при величине q=1 и качестве обслуживания P=0.005

Тип многозвенной коммутационной системы (МКС)— 20х20х3.

Параметры блока ГИ — 80х120х400.

Нагрузка на выходы блока ГИ — Y_бл=45 Эрл. вызовов маркером при заданных условиях.

P(γ>2)=0.005=P_норм – норма качества обслуживания;

h_МГИ=0.5 с – время обслуживания одного вызова маркером ГИ;

t_д=1 с – допустимое время ожидания;

t_вх=75,9505 90.8257 с — время занятия входа коммутационного поля;

Y_бл=42.5 Эрл – допустимая нагрузка на входы блока ГИ.

2) Для заданного блока ГИ методом эффективной доступности рассчитать число линий в НПД пучке для направления от АТСК-3 к проектируемой АТСЭ-4 при величине q=1 и качестве обслуживания P=0.005.

Тип многозвенной коммутационной системы прежний (см. выше).

Прочие параметры прежние (см. выше).

Решение:

1) Приступим к решению первой задачи.

а) Нагрузка на один блок ГИ:

б) Для σ>1 необходимо воспользоваться формулой:

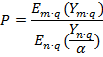
в) Требуется подобрать такое , чтобы потери были равны 0.005. Методом подбора определим, что данное условие выполняется при значении :

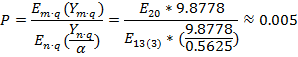
 Г) Далее необходимо найти такое , чтобы нижерасположенное выражение равнялось норме потерь:

Д) Берется  и рассчитывается дляq=1, m=20 и n=13.(3):

Полученная величина меньше, чем требуемая, поэтому надо брать другие значения. Условие P=0.005 выполняется при

Е) Далее считается число линий в НПД пучке:

2) Перейдем к решению задачи 2.

A) Минимальная доступность:

Б) Математическое ожидание доступности при связности f=1

Тогда:

В) Эффективная доступность при коэффициенте связности θ=0.75 будет равняться:

 Г) Далее требуется воспользоваться таблицей значений коэффициентов α и β для расчёта числа линий V по формуле О Делла. Однако, по причине присутствия там только целочисленных значений α и β нам потребуется провести 2 интерполяции.

Величина α задана при P=0.005 - (для =11 : α=1.62 и =12 : α=1.55 ) и следовательно при =11.292 после проведения интерполяции будет равняться:

Д) Величина β задана для P=0.005 - при =11 ( β=3.6 ), а также при значении =12 ( β=3.9 ), следовательно после интерполяции:

Е) Подставим полученные после интерполяции параметры в формулу для нахождения числа линий:

=1.5996⋅80.3682+3.6875≈ 133

Приложение

Таблица вариантов на лабораторную работу №3

Скачано с www.znanio.ru