Лабораторная работа по информатике и ИКТ

ЛАБОРАТОРНАЯ РАБОТА №5 РАБОТА С ПАКЕТОМ MATHCAD. ЧИСЛЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ОБРАБОТКА ДАННЫХ

ЦЕЛЬ РАБОТЫ

Познакомится с возможностями пакета MathCAD.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Для поиска функции, удовлетворяющей обыкновенному дифференциальному уравнению (ОДУ) в заданном диапазоне значений, можно использовать блоки решения.

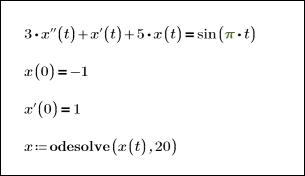
Здесь выходная функция рассчитана в диапазоне 0 ≤ x ≤ 20:

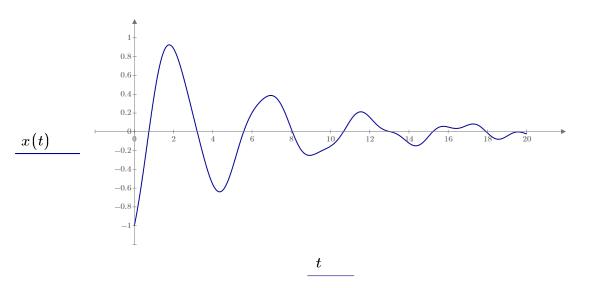
При использовании ОДУ в блоках решения необходимо учитывать следующие ограничения.

·        Для решения ОДУ в блоках решения используйте оператор "равно". Не используйте операторы сравнения или неравенства. Для определения

производных используйте оператор производной или оператор штриха.

·        Начальные и граничные условия. Для одного ОДУ n-го порядка должно быть задано n независимых ограничений в форме равенства: Конечные точки, используемые в граничных условиях, должны

соответствовать конечным точкам, указанным в команде odesolve. PTC Mathcad проверяет правильность типа и количества условий и возвращает ошибку при обнаружении несоответствия.

Результат. Результат вычислений функции odesolve необходимо назначить либо имени функции, либо вектору имен функций, без аргументов.

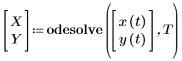
Неявным аргументом для этих функций является переменная интегрирования:

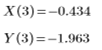
С   помощью встроенных функций анализа данных PTC Mathcad можно получать и анализировать данные, а также управлять ими.

Интерполяция — это процесс поиска промежуточных значений в данных путем подгонки подходящих функций (обычно полиномов) кусочно через соседние точки данных. Данный метод отличается от регрессии, при которой одна функция подгоняется методом наименьших квадратов через все точки данных.

Поскольку функции интерполяции должны проходить через все точки данных, они очень чувствительны к ложным данным. Если данные содержат шумы, следует рассмотреть вариант использования функции регрессии.

·        interp — интерполяция в заданной точке выходных данных функций cspline, lspline, pspline, bspline или loess.

·        bspline, Spline2, Binterp, DWS — интерполяция B-сплайном с заданными пользователем узлами.

·        cspline, pspline, lspline, Bicubic2D — интерполяция кубическим сплайном в одном и двух измерениях с кубическими, параболическими и линейными условиями на концах.

·        linterp — линейная интерполяция.

·        predict — линейный прогноз.

·        polyint, polycoeff, polyinter — полиномиальная интерполяция.

·        rationalint — интерполяция рациональной функцией.

·        Thielecoeff, Thiele — непрерывная дробная интерполяция Тиле. linterp(vx, vy, x): возвращает полученное линейной интерполяцией

значение в точке x для векторов данных vx и vy.

Функция linterp выполняет линейную интерполяцию в запрошенной точке x, рассчитывая промежуточные значения между соседними точками данных линии наилучшего приближения. Для значений x вне диапазона данных функция linterp экстраполирует прямую линию между двумя первыми или последними точками.

Аргументы

·        vx является вектором значений вещественных данных в порядке возрастания.

·        vy является вектором значений вещественных или комплексных данных, имеющих то же количество элементов, что и vx.

·        x является значением независимой переменной, для которого интерполируется результат. Для получения наилучших результатов переменная x должна располагаться в интервале между значениями vx.

Пример использования функции linterp, чтобы выполнить линейную интерполяцию.

Определяется набор значений y.

Определяется согласующийся набор значений x. Эти значения должны располагаться в возрастающем порядке.

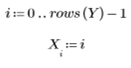
Определяется вектор значений x, для которых нужно интерполировать кривую.

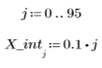
Вызывается функция linterp, чтобы выполнить линейную интерполяцию между точками данных.

График для точек данных и интерполированной кривой.

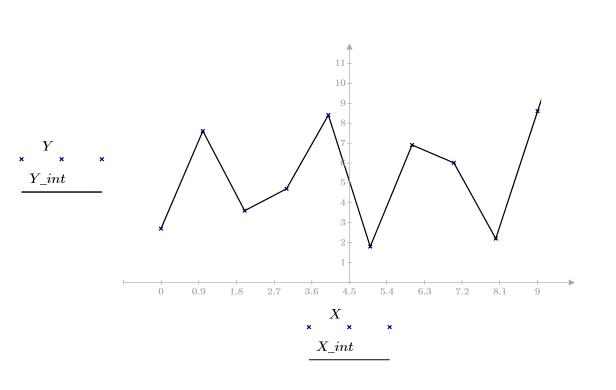
Функция linterp выглядит как прямая линия между наборами точек данных. Интерполяция подразумевает, что функция последней аппроксимации, рассчитанная между последними двумя точками, остается истинной для всех других точек на этом конце диапазона. Допущения редко бывают приемлемы. Существуют различные методы прогнозирования значений за пределами диапазона данных.

Функция interp в интерполяции и регрессии используется для интерполяции в данной точке выходных данных одной из следующих функций: cspline, lspline, pspline, bspline или loess. interp(vs, vx, vy, x) или interp(vs, Mxy, Mz, X): возвращает интерполированное значение в точке x из коэффициентов вектора vs и исходные данные в vx и vy. При подгонке поверхности X является двухэлементным вектором, для которого рассчитываются интерполированные значения z.

Аргументы

·        vs является вектором, созданным одной из следующих функций: cspline(vx, vy), lspline(vx, vy), pspline(vx, vy) и др.

·        vx и vy являются векторами одинаковой длины, состоящими из вещественных значений.

·        x является вещественным значением независимой переменной, для которого требуется рассчитать кривую интерполяции. Для получения наилучших результатов это значение должно быть в диапазоне значений vx.

·        Mxy — массив n x 2 независимых вещественных данных, задающих координаты x и y относительно диагональной или прямоугольной сетки. Поэтому необходимо иметь одинаковое число значений x и y в точках независимых данных.

·        Mz — массив n x n вещественных данных. Это значения z, соответствующие значениям x и y в Mxy.

·        X является вещественным двухэлементным вектором значений, для которого требуется рассчитать поверхность интерполяции.

При  осуществлении  аппроксимации  кривой  проводится  подгонка

одиночной функции по всем точкам данных методом наименьших квадратов. Этот метод отличается от интерполяции, при которой кусочные функции подгоняются по смежным точкам данных.

Для дальнейшего анализа данных или определения приемлемости выбранной регрессии может понадобиться применить другие статистические функции, предназначенные для анализа данных.

Линейная и медиан-медианная регрессия

·        line, slope, intercept, stderr — линейная регрессия по методу наименьших квадратов для данных и среднеквадратическая ошибка, связанная с линейной регрессией.

·        medfit — медиан-медианная линейная регрессия для данных. Полиномиальная регрессия и регрессия рациональной функции

·        loess — локализованная полиномиальная регрессия.

·        rationalfit, rationalfitnp — регрессия рациональной функции по методу наименьших квадратов.

·        polyfit, polyfitc, polyfitstat — многомерная полиномиальная регрессия. Нелинейная регрессия

·        genfit — нелинейная регрессия по методу наименьших квадратов для произвольных функций подгонки.

·        expfit — экспоненциальная регрессия по методу наименьших квадратов.

·        lnfit, logfit — логарифмическая регрессия по методу наименьших квадратов.

·        lgsfit — регрессия логистической кривой по методу наименьших квадратов.

·        pwrfit — регрессия кривой мощности по методу наименьших квадратов.

·        sinfit — синусоидальная регрессия по методу наименьших квадратов.

Довольно часто используется линейная регрессия, при которой аппроксимирующая функция y(x) имеет вид y(x) = a + bx , для определения коэффициентов которой в MathCAD служат следующие встроенные функции:

·        intercept(VX, VY) – возвращает значение параметра a (величины отрезка, отсекаемого линией регрессии на оси OY);

·        slope (VX, VY) – возвращает значение параметра b (тангенса угла наклона линии регрессии).

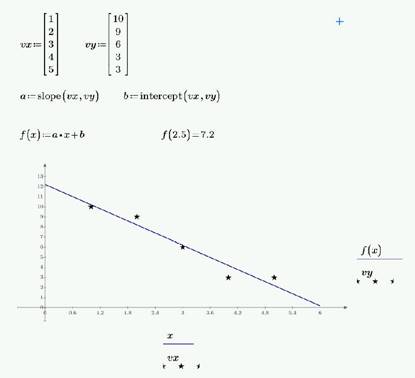
polyfit(X, Y, n) определяет функцию, описывающую поверхность многомерной полиномиальной регрессии, которая подгоняет результаты, записанные в матрице Y, к данным, найденным в матрице X. Уравнение полиномиальной регрессии можно определить, задав степень полинома n.

Например, функция полиномиальной регрессии p:

p := polyfit(X, Y ,1)

p(v) = 1.075

Функция p берет векторный аргумент v, указывающий значение для каждой независимой переменной p, как описывается матрицей X. Каждая переменная вектора v должна иметь единицы, совместимые с соответствующим столбцом матрицы X. Единицы измерения, возвращаемые аппроксимирующей функцией p, совместимы с единицами измерения матрицы Y.

Аргументы

·        X — матрица плана или матрица, в которой каждый столбец представляет независимую переменную. Каждый столбец X должен иметь совместимые единицы измерения.

·        Y — вектор или матрица с результатами измерений или моделирования, где каждая строка содержит результаты отдельного выполнения или точку данных, определенную в X. Если строки содержат неодинаковое число реплик, необходимо заполнить пустые элементы Y значениями NaN. Элементы матрицы Y должны иметь совместимые единицы измерения.

·        n — целое число, задающее степень полинома. Оно должно быть меньше общего числа точек данных: 1 ≤ n ≤ length(Y) − 1. В противном случае задача недостаточно ограничена и не имеет уникального решения.

ЗАДАНИЕ

Упражнение     1.      Найти     численное    решение    дифференциального

уравнения в MathCAD на интервале x∈[0, 20]. Построить график решения.

Упражнение 2. Выполнить в MathCAD заданного вида интерполяцию табличных данных y = f (x). Построить графики.

Аппроксимировать таблично заданную зависимость y = f (x) указанной функцией с помощью регрессионного анализа. Построить графики.

Упражнение 3. Определить количество тепла необходимое чтобы нагреть 2 литра воды на 50 °С. Решить задачу используя встроенные размерности.

Упражнение 4. Мяч бросается со скоростью 100 м/с под углом к горизонту 45 градусов. На мяч действует только сила тяжести. Необходимо построить траекторию полета мяча и определить координаты максимально высокой точки. Решить задачу используя встроенные размерности.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.     Назовите способы решения дифференциальных уравнений в MathCAD.

2.     Назовите методы интерполяции и регрессионного анализа, используемые в MathCAD.