Лабораторная работа по информатике и ИКТ

ЛАБОРАТОРНАЯ РАБОТА №9 РАБОТА С ПАКЕТОМ MICROSOFT EXCEL. ДИАГРАММЫ

ЦЕЛЬ РАБОТЫ

Привить у студентов навыки построения и редактирования диаграмм в

Microsoft Excel и печати рабочих листов.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Типы диаграмм (основные)

·        Круговая – используется для отображения относительного соотношения между частями целого.

·        Линейчатая – для сравнения значений между частями целого.

·        Гистограмма – похожа на линейчатую. Используется для показа соотношения между частями целого.

·        График – для отображения тенденций изменения данных за равные промежутки времени.

·        Точечная – для отображения различий между значениями в двух рядах.

·        С областями – для подчеркивания величины изменения в течении определенного промежутка времени.

Большинство из этих диаграмм могут быть объемными, что помогает подчеркнуть различия между разными наборами данных. Excel поддерживает много других типов диаграмм.

Термины, используемые при построении диаграмм:

Ряды данных – это графические элементы диаграмм: полосы, сектора, линии и т.п. Обычно ряды данных располагаются в строках на рабочем листе.

Категории – отображают количество элементов в ряду. (Например, 2 ряда для сравнения объемов продаж в 2-х разных магазинах и 4-х категориях по кварталам.) Обычно категории располагаются в солбцах на рабочем листе, а названия категорий - в заголовках столбцов.

Ось – одна из сторон диаграммы. По оси X отображаются все категории

и   ряды данных в диаграмме. Если в диаграмме есть несколько категорий, то на оси X обычно отображаются подписи к категориям.

На оси Y отображаются все значения полос, линий или точек графика. В объемных диаграммах ось Z направлена вертикально.

Легенда – описание отдельных элементов диаграммы.

Сетка – продолжение деления осей, улучшает восприятие и анализ данных.

Для построения диаграммы прежде всего необходимо выделить ячейки, содержащие данные, которые должны быть отражены на диаграмме.

Если необходимо, чтобы в диаграмме были отражены названия строк или столбцов, надо выделить также содержащие их ячейки.

После этого следует нажать кнопку «Мастер диаграмм» на стандартной панели инструментов. Мастер диаграмм работает в 4 шага:

На 1-м шаге необходимо выбрать тип диаграммы в списке слева. (Заметим, что типы диаграмм делятся еще на стандартные и нестандартные. Для выбора соответствующего списка надо щелкнуть вкладку в верхней части окна.) Внешний вид диаграммы мы выбираем, щелкнув соответствующий рисунок в правой части окна. Для перехода ко 2-му шагу следует нажать кнопку «Далее».

На 2-м шаге в средней части окна можно увидеть приблизительно внешний вид будущей диаграммы и, если он не будет соответствовать ожидаемому результату, то в этот момент можно изменить диапазон исходных данных для построения диаграммы. Для перехода ко 3-му шагу следует нажать кнопку «Далее».

На 3-м шаге, если необходимо, можно изменить или установить параметры целого ряда элементов диаграммы: заголовков, осей, линий сетки, легенды, подписей данных и т.п. Для этого надо щелкать соответствующие вкладки в верхней части окна. Для перехода ко 4-му шагу следует нажать кнопку «Далее».

На 4-м шаге мы определяем, где будет располагаться построенная нами диаграмма - на отдельном или на имеющемся листе рабочей книги. После этого следует нажать кнопку «Готово».

Заметим, что существует очень быстрый способ построения одного из типов диаграмм - гистограммы на отдельном листе. Необходимо только выделить нужный диапазон и нажать клавишу F11.

После того, как диаграмма построена, можно изменить ее внешний вид. Для этого можно использовать либо панель инструментов «Диаграммы», либо отмечать щелчком мыши различные элементы диаграммы и затем, нажав правую кнопку мыши, выбирать необходимую команду из списка.

ЗАДАНИЕ

Качество работы ТЭС оценивается, прежде всего, ее коэффициентом полезного действия, удельными расходами условного топлива на выработку тепловой и электрической энергии.

Расход топлива на выработку отпускаемой потребителю тепловой энергии условно считают таким же, как и при ее выработке непосредственно в паровом котле. Тогда

,

коэффициент полезного действия котла.

Расход топлива на выработку электроэнергии определяется формуле:

ка  –

по

В э

год

=

В  -

Вт год

,

где В – общий расход топлива на ТЭС (т/ч, кг/с).

При  таком  методе  расчета  вся  выгода  от  совместной выработки

теплоты и электроэнергии приходится на долю электроэнергии.

Основой для выполнения расчета показателей режима работы ТЭС по вышеизложенным формулам является правильное определение количества вырабатываемой электроэнергии Э_год и теплоты Q_год , вычисляемые через значения определенных интегралов в зависимости от вида функций соответственно N (t) и Q(t) .

Для обеспечения надежной и эффективной работы электростанции необходимо знать изменение потребления энергии по времени. Изменение потребления энергии по времени обычно изображается диаграммой, которая называется графиком нагрузки. Графики нагрузки могут быть суточными, месячными и годовыми. Площадь, ограниченная кривой годового графика, представляет собой в масштабе количество выработанной станцией за год энергии, т.е. - годовая выработка электроэнергии:

8760

Э_год  = ò N (t)dt

0                 ,

-  годовая выработка тепловой энергии:

.

Аналогично годовому строятся

В     прикладных исследованиях часто значения определенного интеграла:

суточные и месячные графики нагрузок. возникает необходимость вычисления

непрерывная функция на отрезке [a, b].

Этот интеграл можно трактовать как площадь фигуры, объем, работу переменной силы и т.д., ограниченной ординатами a и b , осью абсцисс X и графиком подынтегральной функции f (x) .

Способы задания или получения зависимостей N (t) и Q(t) могут быть

различны (таблично, аналитически и т.д.), но та и другая функции могут быть интерпретированы как непрерывные функции f (x) .

Если функция f (x) непрерывна на отрезке [a, b] и ее первообразную удается выразить через известные функции, то для вычисления интеграла можно воспользоваться формулой Ньютона-Лейбница:

I

=  F(b) -

F (a)

.

Однако в большинстве случаев аналитическое выражение для первообразной найти не удается, даже если подынтегральная функция содержит элементарные функции, а во многих решениях под интегралом содержатся специальные функции (например, функция Бесселя). В этих случаях приходится прибегать к численному интегрированию.

Сущность большинства методов вычисления определенных интегралов

состоит    в    замене    подынтегральной    функции     f (x)     аппроксимирующей

функцией j(x) , для которой можно легко записать первообразную в элементарных функциях, т.е.:

применяется соответствующая простая формула. Таким образом, получают составные формулы численного интегрирования. Используемые на практике методы численного интегрирования можно классифицировать в зависимости от способа аппроксимации подынтегральной функции на следующие группы:

1.     методы Ньютона-Котеса, основанные на полиномиальной аппроксимации (метод прямоугольников, трапеций, метод Симпсона и т. д.);

2.     сплайновые методы, базирующиеся на аппроксимации подынтегральной функции сплайнами, представляющими собой кусочный полином;

3.     методы наивысшей алгебраической точности (методы Гаусса – Кристоффеля и др.), использующие неравноценные узлы, расположенные по алгоритму, обеспечивающему минимальную

погрешность интегрирования при заданном количестве узлов.

Метод прямоугольников – простейший прием численного интегрирования, при котором функция y = f (x) заменяется интерполяционным многочленом нулевого порядка. Для повышения точности интегрирования отрезок [a, b] разбивается на m частей и формула прямоугольника применяется к каждому отрезку. При реализации метода прямоугольников возможно три варианта его модификации: метод левых, правых и средних прямоугольников.

Обобщенная формула прямоугольников выглядит следующим образом:

_{I   »} b - a _å^m-1 _yi ^m i =0 _.

Алгоритм численного интегрирования по методу средних прямоугольников представлен на рис.

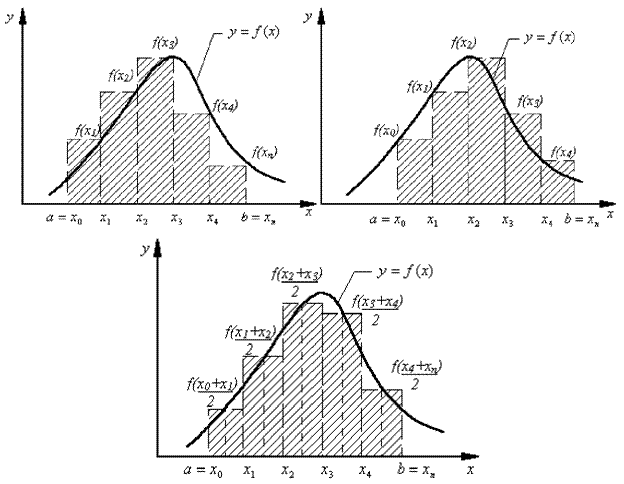
Численное интегрирование методом прямоугольников:

a.     метод левых прямоугольников;

b.     правых прямоугольников;

c.      средних прямоугольников

Вследствие  низкой  точности  метод  прямоугольников  широкого

распространения не получил.

Согласно методу трапеций подынтегральную функцию заменяют на

участке

+

h]

,    где

полиномом первой степени. Как и в методах

прямоугольников, такая аппроксимация неоднозначна. Одним из возможных способов является проведение прямой через значения функции на границах интервала интегрирования.

В        этом случае приближенное значение интеграла определяется суммой площадей трапеций:

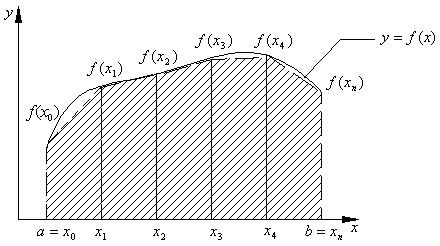
Эта формула соответствует приближенной замене площади некоторой криволинейной трапеции площадью фигуры, ограниченной ломаной линией, проходящей через точки f (x0 ) , f (x1 ) , f (x2 ) , … , f (xm ) :

f  (x0 ) + 2

.

Графическая иллюстрация метода трапеций

По исходным данным, приведенным в таблице разработать алгоритм определения показателей режима работы ТЭС (коэффициент полезного действия и удельные расходы условного топлива по выработке тепловой и электрической энергии).

Исходные данные к лабораторной работе

Вариант

01, 21,41, 61,

81

02, 22, 42, 62,

82

03, 23, 43, 63,

83

04, 24, 44, 64,

84

05, 25, 45, 65,

85

06, 26, 46, 66,

86

07, 27, 47, 67,

87

08, 28, 48, 68,

88

09, 29, 49, 69,

89

Часы года, ч

Нагрузка, МВт,

МДж                 0 1220250037805010620075008760

h_ка ,

%

93.5

90.8

91.3

92.6

93.7

91.2

94.4

91.9

92.1

Q р ,

н

МДж∙кг

19.8

15.6

17.5

21.5

24.2

16.7

23.1

19.6

20.9

Вэ

год

В т

год

0.55

0.63

0.74

0.91

0.88

0.83

0.97

0.49

0.75

Вариант

10, 30, 50, 70,

90

11, 31, 51, 71,

91

12, 32, 52, 72,

92

13, 33, 53, 73,

93

14, 34, 54, 74,

94

15, 35, 55, 75,

95

16, 36, 56, 76,

96

17, 37, 57, 77,

97

18, 38, 58, 78,

98

19, 39, 59, 79,

99

20, 40, 60, 80,

00

Нагрузка, МВт,

МДж

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

N (t)

Q(t)

Часы года, ч

0 1220250037805010620075008760

75       85  110 160 225 285 350 380

100 550 750 800 805 780 625 300

400 390 375 340 280 215 150 100

500 425 345 300 295 300 450 600

275 335 340 375 350 260 185 125

100 105 150 350 575 725 790 815

50       65  160 360 375 275 175 140

700 675 640 600 570 530 500 460

175 250 285 320 380 345 340 335

120 125 130 175 250 450 600 750

200 205 225 235 260 280 300 305

500 550 650 700 650 560 480 420

195 270 300 335 360 355 350 345

145 155 160 175 250 450 400 350

600 550 425 235 260 280 310 325

345 510 550 600 620 570 510 490

325 350 385 320 280 295 310 315

225 250 330 375 450 480 420 400

405 365 325 335 360 380 400 405

250 350 450 500 450 360 280 220

75     150 185 220 280 245 230 220

25     100 130 175 250 300 320 310

hка ,

%

93.6

94.2

92.4

90.6

89.9

91.8

93.9

92.5

88.8

90.0

89.3

Q р ,

н

МДж∙кг

24.7

18.1

17.0

22.3

15.4

19.2

12.4

19.8

14.6

21.9

19.4

Вэ

год

В т

год

0.62

0.95

0.77

0.81

0.96

0.79

0.83

0.69

0.94

0.77

0.90

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.                 Сколько шагов содержит Мастер диаграмм?

2.                 Как удалить из диаграммы столбец данных?

3.                 Как в диаграмме изменить порядок рядов данных?

4.                 Для какого количества данных можно построить круговую диаграмму?

5.                 Как добавить данные в уже имеющуюся диаграмму?