Добавить материал

и получить 10 документов
и свидетельство автора

Егорова Альбина Григорьевна

Лабораторная работа по информатике и ИКТ

docx
29.05.2021

Публикация педагогических разработок

Бесплатное участие. Свидетельство автора сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

ЛАБОРАТОРНАЯ РАБОТА №2 РАЗРАБОТКА БЛОК-СХЕМ.docx

ЛАБОРАТОРНАЯ РАБОТА №2 РАЗРАБОТКА БЛОК-СХЕМ АЛГОРИТМОВ.

ОЗНАКОМЛЕНИЕ С MICROSOFT VISIO.

ЦЕЛЬ РАБОТЫ

Научить составлять блок-схемы для различных типов алгоритмов.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Понятие алгоритма так же фундаментально для информатики, как и понятие информации. Решение задач на компьютере основано на понятии алгоритма. Алгоритм – это точное предписание, определяющее вычислительный процесс, ведущий от варьируемых начальных данных к исходному результату.

Применительно к ЭВМ алгоритм определяет вычислительный процесс, начинающийся с обработки некоторой совокупности возможных исходных данных и направленный на получение определенных этими исходными данными результатов.

Если вычислительный процесс заканчивается получением результатов, то говорят, что соответствующий алгоритм применим к рассматриваемой совокупности исходных данных. В противном случае говорят, что алгоритм неприменим к совокупности исходных данных. Любой применимый алгоритм обладает следующими основными свойствами:

Результативность означает возможность получения результата после выполнения конечного количества операций.

Определенность состоит в совпадении получаемых результатов независимо от пользователя и применяемых технических средств.

Массовость заключается в возможности применения алгоритма к целому классу однотипных задач, различающихся конкретными значениями исходных данных.

Дискретность означает разбиение алгоритма на конечную последовательность действий или шагов при его выполнении.

Конечность означает то, что алгоритм должен выполняться за конечное время.

Для задания алгоритма необходимо описать следующие его элементы:

· набор объектов, составляющих совокупность возможных исходных данных, промежуточных и конечных результатов;

· правило начала;

· правило непосредственной переработки информации (описание последовательности действий);

· правило окончания;

· правило извлечения результатов.

Линейным называется алгоритм, в котором выполняются все этапы решения задачи строго последовательно. Это означает, что он не содержит проверок условий и повторений. Блок схема алгоритма выглядит, как последовательность действий.

Графический способ описания алгоритма (блок - схема) получил самое широкое распространение. Для графического описания алгоритмов используются схемы алгоритмов или блочные символы (блоки), которые соединяются между собой линиями связи.

Каждый этап вычислительного процесса представляется геометрическими фигурами (блоками). Они делятся на арифметические или вычислительные (прямоугольник), логические (ромб) и блоки ввода-вывода данных (параллелограмм).

Таблица. Основные символы для схем алгоритмов

Название символа	Обозначение и	Пояснение
Название символа	пример заполнения	Пояснение
	пример заполнения
Процесс		Вычислительное действие или
Процесс		последовательность действий
		последовательность действий

Предопределенный		Вычисления по
Предопределенный		подпрограмме, стандартной
процесс		подпрограмме, стандартной
процесс		подпрограмме
		подпрограмме

Решение		Проверка условий

Ввод-вывод		Ввод-вывод в общем виде

Пуск-останов		Начало, конец алгоритма,
Пуск-останов		вход и выход в подпрограмму
		вход и выход в подпрограмму

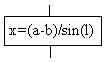
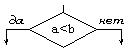
Порядок выполнения этапов указывается стрелками, соединяющими блоки. Геометрические фигуры размещаются сверху вниз и слева на право. Нумерация блоков производится в порядке их размещения в схеме.

По структуре выполнения алгоритмы и программы делятся на три вида:

линейные, ветвящиеся, циклические.

Линейный алгоритм (линейная структура) – это такой алгоритм, в котором все действия выполняются последовательно друг за другом и только один раз. Схема представляет собой последовательность блоков, которые располагаются сверху вниз в порядке их выполнения. Первичные и промежуточные данные не оказывают влияния на направление процесса вычисления.

На практике часто встречаются задачи, в которых в зависимости от первоначальных условий или промежуточных результатов необходимо выполнить вычисления по одним или другим формулам.

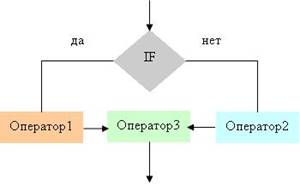
Такие задачи можно описать с помощью алгоритмов разветвляющейся структуры. В таких алгоритмах выбор направления продолжения вычисления осуществляется по итогам проверки заданного условия. Ветвящиеся процессы описываются оператором IF (условие ЕСЛИ).

Для решения многих задач характерно многократное повторение отдельных участков вычислений. Для решения таких задач применяются алгоритмы циклической структуры (циклические алгоритмы).

Цикл – последовательность команд, которая повторяется до тех пор, пока не будет выполнено заданное условие. Циклическое описание многократно повторяемых процессов значительно снижает трудоемкость написания программ.

Существуют две схемы циклических вычислительных процессов.

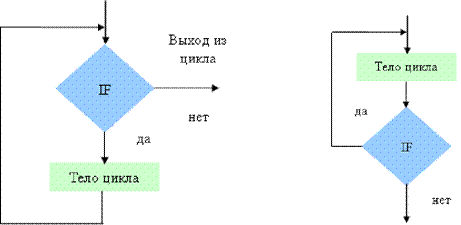
Особенностью первой схемы является то, что проверка условия выхода из цикла проводится до выполнения тела цикла. В том случае, если условие выхода из цикла выполняется, то тело цикла не выполняется ни разу.

Особенностью второй схемы является то, что цикл выполняется хоты бы один раз, так как первая проверка условия выхода из цикла осуществляется после того, как тело цикла выполнено.

СОЗДАНИЕ БЛОК-СХЕМ В MICROSOFT VISIO

Графический редактор Visio обладает множеством особенностей. К одной из таких особенностей относится наличие встроенных мастеров, позволяющих создавать блок-схемы различных уровней сложности. В Visio имеется несколько стандартных типов блок-схем, с помощью которых можно быстро строить схемы в тех областях, где они используются наиболее часто:

· Audit Diagram (аудиторская диаграмма) – блок-схема ревизии – включает фигуры, используемые в схемах контроля, учета и управления финансовыми или информационными потоками;

· Basic Flowchart (основная блок-схема) – блок-схема общего назначения – применяется для создания пользовательских блок-схем произвольного назначения или добавления необходимых элементов в стандартные схемы;

· Cause and Effect Diagram (причинно-следственная диаграмма) –

блок-схема, позволяющая проиллюстрировать причинную зависимость событий;

· Cross-Functional Flowchart (перекрестно-функциональная блок-

схема) – надстройка блок-схемы, которая предназначена для иллюстрации отношений между изменением процесса выполнения задачи и его организацией;

· Data Flow Diagram (диаграмма временного потока) – блок-схема,

содержащая элементы, которые зависят от времени или условия;

· IDEFO Diagram (IDEFO-диаграмма) – блок-схема, позволяющая создавать зависимые или многоуровневые диаграммы;

· Mind Mapping Diagram (отображающая диаграмма) – блок-схема,

предназначенная для представления проектов, находящихся в стадии разработки или усовершенствования;

· SDL Diagram (SDL-диаграмма) – блок-схема, в которой используются графические элементы языка SDL (Specification and Description Language, язык спецификации и описаний). Эта блок-схема содержит фигуры стандартных элементов языка SDL, с помощью которых можно создавать профессиональные блок-схемы, например блок-схемы программ;

· TQM Diagram (TQM-диаграмма) – блок-схема, предназначенная для представления управления и автоматизации процесса;

· Work Flow Diagram (диаграмма распределения рабочего потока) –

блок-схема для представления процесса управления, учета и

изменения человеческих ресурсов.

Перечисленных типов достаточно для создания блок-схем любой сложности. Каждый тип имеет свой трафарет, в котором содержатся соответствующие мастера.

Для соединения элементов схемы можно использовать соединители (connectors) из текущего трафарета или выбрать понравившийся соединитель

в специальном трафарете. Использование нестандартных соединителей позволяет украсить создаваемую схему и сделать ее более понятной и привлекательной. После завершения создания блок-схемы ее можно украсить: выполнить заливку элементов схемы.

ЗАДАНИЕ

Составьте блок-схему для решения следующей задачи, используя

простые операторы:

Вариант	Задание
	Дана функция = ∙ ² + ∙ + . Коэффициенты , , являются
01, 26,	константами, а находится в интервале [– 10, 18] и изменяется с
51, 76	шагом ℎ, значение которого вводится с клавиатуры. Найти все
	значения функции для заданных .
02, 27,	Дана функция = 2⁻¹ + 3. Найти значение переменной , при

52, 77

котором значение функции превысит = 1000.

Найти значение функции. В

данной функции , ,

–

const, –

03, 28,

вводится с клавиатуры.

при

≥ 3

53, 78

∙ − ,

при

∈ (−5.5, 3)

{

³,

при

≤ −5.5

04, 29,

Найти число натуральных чисел таких,

что ² + ³ ≤ , где

54, 79

– заданное натуральное число.

05, 30,

Найти число

натуральных

чисел

= 1 …

сумму

S = ∑₌₁

так,

чтобы выполнялось

условие £ ,

где –

55, 80

заданное натуральное число.

06, 31,

Найти число натуральных чисел = 1 … таких,

что и ² <

и вычислить сумму S = ∑₌₁

( − )²

, а – заданные числа, –

56, 81

, где

натуральное число.

07, 32,

Найти число натуральных чисел

= 1 … таких, что и ³ <

и вычислить сумму S = ∑₌₁

( − )²

, а – заданные числа, –

57, 82

, где

натуральное число.

Пользуясь

тем,

что

cos( ) = 1 −

⁴

−⋯+(−1)

(2 )!

08, 33,

вычислить значение ( ) для указанного значения , заданного

радианах,

точностью

= 0.001 .

Точность

вычисления

58, 83

считается выполненной, если последний по модулю член в сумме

меньше e.

Пользуясь тем,

что = 1 + 1 +

+ ⋯ +

вычислить значение

09, 34,

e = 0.0001 .

точностью

Точность

вычисления

считается

59, 84

выполненной, если последний член в сумме меньше e.

Для

числовой

последовательности

( – 1)/ ² ,

1,2,…

где e –

10, 35,

Найти первый член и его номер такой,

чтобы

60, 85

заданное

число,

например,

e = 0.001

вычислить

сумму

S =

_∑

Для числовой последовательности = √

− √

, = 1,2,…

+ 1

11, 36,

найти первый член и его номер такой,

чтобы

где e –

61, 86

заданное

число,

например,

e = 0.001

вычислить

сумму

S =

_∑

Для числовой последовательности

∙ ( )

1, 2, … , найти

12, 37,

²+1

e , где e –

первый член и его номер такой,

чтобы | |

62, 87

заданное

число,

например,

e = 0.001

вычислить

сумму

S =

_∑

13, 38,

Для

числовой

последовательности

₂ +1₊₄ +1

, =

1,2,…

63, 88

2 +4

найти первый член и его номер такой, чтобы | – 4| < e, где e

– заданное число, например, e = 0.01 и вычислить сумму

S =

_∑

Найти наименьшее натуральное число , кратное 5, для которого

14, 39,

√1+| |

< e,

где e = 0,01, –

заданное число и вычислить сумму

64, 89

S =

∑₌₁

Найти наименьшее натуральное число , кратное 3, для которого

15, 40,

√ +| |

< e,

где e

= 0.01, – заданное число и вычислить сумму

65, 90

∑₌₁

S =

Найти наименьшее натуральное число , кратное 4, для которого

16, 41,

+| |

< e, где e = 0.01, –

заданное

число и

вычислить

сумму

66, 91

S =

∑₌₁

₂

Найти наименьшее натуральное число , кратное 6, для которого

17, 42,

| |

67, 92

< e, где e = 0.01, –

заданное число и

вычислить

сумму

S =

∑₌₁

+| |

18, 43,

Найти

наименьшее

натуральное

число такое, для

которого

= 0.01 и вычислить сумму S = ∑₌₁

₍₋₁₎ −1

68, 93

−

| < e, где e

2 +4

2 −1

Найти

наименьшее

натуральное

число такое, для

которого

19, 44,

−

²− +1

| < e

где

e = 0.01

вычислить

сумму

69, 94

2 ²+2

S =

∑₌₁

₍₋₁₎ −1

√

Найти

наименьшее

натуральное

число такое, для

которого

20, 45,

−

1− ( )

| < e , где e = 0.01 ,

= 1/ и

вычислить

сумму

70, 95

S =

∑₌₁

2 −1

Найти

наименьшее

натуральное

число такое, для

которого

21, 46,

|1 −

( )

|<e,

где e = 0.01 , = 1/

вычислить

сумму

71, 96

(−1)⁻¹

S =

∑₌₁

Для указанного значения найти наименьшее натуральное число

22, 47,

такое,

что

|<e ,

где e

= 0.01

вычислить

сумму

72, 97

S =

∑₌₁

Найти

корень уравнения 5 ³ + 10 ² + 5 − 1 = 0 с точностью

23, 48,

e = 0.001,

пользуясь формулой ₊₁

, где = 0, 1, …,

5( +1)

73, 98

₀=0.

Точность

вычисления

считается

достигнутой,

если

| ₊₁ − | < e.

24, 49,	Найти	корень уравнения ³ + 12 − 2 = 0							с	точностью e =
24, 49,						2− ³
	0.001,	пользуясь формулой		=			,	где = 0,1, …, = 0.1.
	0.001,	пользуясь формулой		=			,	где = 0,1, …, = 0.1.
74, 99		+1				12				0
	Точность вычисления считается достигнутой, если \| ₊₁ − \| < e.
	Найти	корень уравнения 2 ³ + 4 − 1 = 0							с	точностью e =
25, 50,	0.001, пользуясь формулой		=			1		, где = 0,1, …, = 0.2.
25, 50,	0.001, пользуясь формулой		=		2(2+ ³)			, где = 0,1, …, = 0.2.
75, 00		+1			2(2+ ³)					0
75, 00
	Точность вычисления считается достигнутой, если \| ₊₁ − \| < e.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Отличительные особенности алгоритмов с предусловием и постусловием.

2. Какие условные обозначения блоков схем алгоритмов существуют?

3. Какие элементарные алгоритмические структуры существуют?

Линейным называется алгоритм, в котором выполняются все этапы решения задачи строго последовательно

Порядок выполнения этапов указывается стрелками, соединяющими блоки

Особенностью первой схемы является то, что проверка условия выхода из цикла проводится до выполнения тела цикла

Data Flow Diagram (диаграмма временного потока) – блок-схема, содержащая элементы, которые зависят от времени или условия; ·

Найти значение функции. В данной функции , , – const, – 03, 28, вводится с клавиатуры

Найти корень уравнения 3 + 12 − 2 = 0 с точностью e = 2− 3 0

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также