Лекции на повторение школьного курса математики

Глава 1. Тригонометрические функции

Урок 7.  Числовая окружность

Цели урока:  ввести понятие числовой окружности; сформулировать умения записывать множество чисел, соответствующих на числовой окружности  точке; закрепить умение находить на числовой окружности точку, соответствующую данному числу.

Ход урока

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                 II.  Проверка домашнего задания.

Опрос по теории:

1. Какая окружность называется числовой?

2. Где на числовой окружности находятся числа

     ?

3. Как записать множество чисел, соответствующих на числовой окружности  точке?

4. Опишите первый макет числовой окружности.

5. Опишите второй макет числовой окружности.

III.  Закрепление нового материала.

Выходят к доске сразу 4 учащихся и решают №1 одновременно, а остальные учащиеся, решая в тетрадях, проверяют работу у доски. Необходимо создать атмосферу творческого поиска, если будет спор, то умело его поддерживать, и находить верное решение совместно.  Затем по той же схеме решается №3.

На доске изображаются 4 числовые окружности, на которых учащиеся будут показывать точки, которые соответствуют числам из №9-16. Учитель вызывает учащихся к доске без определенного порядка.

IV.  Решение заданий у доски.

Решение заданий из №20, 24, 25 проходит так: учитель решает с полным объяснением у доски в каждом номере букву  (а), а остальные буквы в заданиях решают у доски учащиеся.

Подведение итогов.

Домашнее задание:  №2, 4; теория в учебнике, стр. 8-18; разобрать

пример 7 из теории.

Урок 8. Числовая окружность на  координатной плоскости

Цели урока:   рассмотреть числовую окружность на координатной плоскости; составить таблицу значений; закрепить умение нахождение на числовой окружности точки с конкретным значением абсциссы и ординаты, а также умением определить каким числам они соответствуют.

Ход урока

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                 II.  Проверка домашнего задания.

Проверить домашнюю работу можно проверочной работой в четырех вариантах:

III.  Объяснение нового материала.

Объяснение нового материала (стр. 18-26):

1. Рассмотреть числовую окружность в декартовой системе координат.

2. Составить таблицу координат чисел числовой окружности для первого макета.

3. Составить таблицу координат чисел числовой окружности для второго  макета.

IV.  Закрепление нового материала.

На доске изображаются 4 числовые окружности на координатной плоскости, на которых выполняются задания из №29-34(а, б, в). 

Подведение итогов.

Домашнее задание: №29-34 (г); теория в учебнике, стр. 18-26;

разобрать пример из теории.

Урок 9. Синус и косинус

Цели урока:  ввести понятие синуса и косинуса; рассмотреть их свойства; составить таблицу их значений.

Ход урока 

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                 II.  Проверочная работа.

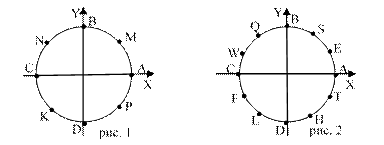
На доске изображаются первый и второй макет числовой окружности на координатной плоскости (смотри рисунок 1 и 2). Работа поводится в четырех вариантах. Все задания приведены в таблице.

III.  Объяснение нового материала.

Объяснение нового материала (стр. 26-28):

1. Ввести понятия синуса и косинуса, как координаты точки единичной окружности.

2. Вывести основное тождество тригонометрии.

IV.  Закрепление нового материала.

Решение заданий из №50-54 (а, г), №55 (а, б), №60, 62. на единичной окружности.

Подведение итогов.

Домашнее задание: №57, 61; теория в учебнике, стр. 26-28;

разобрать пример из теории.

Урок 10.  Синус и косинус

Цели урока:  закрепить понятие синуса и косинуса; рассмотреть решение уравнений вида  и ; вывести формулы  и

Ход урока 

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                 II.  Математический диктант.

Вычислить  и , если  t может принимать значения

, , , , , , , .

III. Объяснение нового материала.

Объяснение нового материала (стр. 28-34):

1. Рассмотреть решение уравнения  на окружности, где принимает одно из значений  (примеры 2 и 6).

2. Рассмотреть решение уравнения на окружности, где принимает одно из значений   (примеры 3 и7)

3. Доказать справедливость равенств  и .

IV.   Решение заданий у доски.

После рассмотрения примера 2 решают №63 (б, г), №64 (а), после примера 6 решают №67 (а, в), после примера 3 решают №63 (а, в),  №64 (б, в, г), после примера 7 решают №67 (б, г).

Подведение итогов.

Домашнее задание: №55 (в, г), №65, 66, 68; теория в учебнике,

стр. 30-34.

Урок 11. Тангенс и котангенс

Цели урока:  ввести определение тангенса и котангенса; рассмотреть их свойства; составить таблицу их значений; закрепить понятие синуса, косинуса, тангенса и котангенса; закрепить умение использовать свойства тригонометрических функций.

Ход урока 

I . Организационный момент.

Приветствие, сообщение темы и задач урока.

II.  Работа с учебником.

Учащиеся читают теоретический материал на стр. 34-37. Учитель по мере прочтения задает вопросы учащимся:

1. Почему тангенсом считается отношение синуса к косинусу?

2. При каких условиях существует тангенс? Почему?

3. При каких условиях существует котангенс? Почему?

4. Как вычисляется тангенс числа?

5. Вычислите , , , .

6. Объясните формулы  и  .

7. Вычислите , , , .

Затем вызываются к доске два учащихся для обобщения прочитанного.

III.  Решение заданий у доски.

Решение заданий из №94 – 96 у доски учащимися из группы А.

Решение заданий из №97, 100 у доски учащимися из группы Б. 

Подведение итогов.

Домашнее задание: №98, 99; теория в учебнике, стр. 34-37.

Урок 12.  Тригонометрические функции числового аргумента

Цели урока:  ввести понятие тригонометрической функции числового аргумента; вывести основные формулы одного аргумента тригонометрических функций; формировать умение упрощать выражения с применением основных формул одного аргумента тригонометрических.

Ход урока  

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                 II. Объяснение нового материала.

Объяснение нового материала (стр. 37-39):

1. Вспомните соотношения, связывающие различные тригонометрические функции одного и того же угла.

2. Решить задачу: «Найти соответствующее значение , , , если известно, что  и .»

III.  Закрепление нового материала.

Решение заданий из №110, 111 устно с места, уточняя какую формулу применяли.

К доске работать выходят по одному 4 учащихся, объясняя подробно, решать задания из №112 (а), №116 (а); №112 (б), №117 (а); №112 (в), №118 (а); №112 (г), №119 (а).

IV.  Решение заданий у доски.

К доске выходят сразу 4 учащихся решать три задания:

V.  Проверочная работа.

Остальные учащиеся решают на месте по вариантам:

Подведение итогов.

Домашнее задание: №115, №116-119 (г); теория в учебнике, стр. 37-39.

Урок 13.  Тригонометрические функции числового аргумента

Цели урока:  закреплять умение упрощать выражения с применением основных формул одного аргумента тригонометрических функций; развить навыки упрощение выражений с применением основных формул одного аргумента тригонометрических функций.

Ход урока

I.  Организационный момент.

Приветствие, сообщение темы и задач урока.

                 II.  Проверочная работа.

Проверить знание теоретического материала можно проверочной работой в четырех вариантах:

III.  Проверка домашнего задания.

Пока 4 учащихся решают у доски №115 остальные устно комментируют промежуточные действия в заданиях №116-119 (г).

             IV. Самостоятельная работа.

Подведение итогов.

Домашнее задание: №120; теория в учебнике, стр. 40-43.