Лекция № 22 МОДЕЛИРОВАНИЕ ЗАВИСИМОСТЕЙ МЕЖДУ ВЕЛИЧИНАМИ

Лекция № 22 МОДЕЛИРОВАНИЕ ЗАВИСИМОСТЕЙ МЕЖДУ ВЕЛИЧИНАМИ

ПЛАН

1.     Величины и зависимости между ними.

2.      Математические модели.

3.     Табличные и графические модели.

1 Величины и зависимости между ними

Содержание данного раздела учебника связано с компьютер­ным математическим моделированием. Применение математичес­кого моделирования постоянно требует учета зависимостей одних величин от других. Приведем примеры таких зависимостей:

1) время падения тела на землю зависит от его первоначальной высоты;

2) давление газа в баллоне зависит от его температуры;

3) уровень заболеваемости жителей города бронхиальной аст­мой зависит от концентрации вредных примесей в городском воздухе.

Реализация математической модели на компьютере (компью­терная математическая модель) требует владения приемами представления зависимостей между величинами.

Рассмотрим различные методы представления зависимостей.

Всякое исследование нужно начинать с выделения количест­венных характеристик исследуемого объекта. Такие характерис­тики называются величинами.

С понятием величины вы уже встречались в курсе информати­ки 7-9 классов. Напомним, что со всякой величиной связаны три основных свойства: имя, значение, тип.

Имя величины может быть смысловым и символическим. Примером смыслового имени является « давление газа », а симво­лическое имя для этой же величины - Р. В базах данных вели­чинами являются поля записей. Для них, как правило, использу­ются смысловые имена, например: ФАМИЛИЯ, ВЕС, ОЦЕНКА и т. п. В физике и других науках, использующих математический аппарат, применяются символические имена для обозначения ве­личин. Чтобы не терялся смысл, для определенных величин ис­пользуются стандартные имена. Например, время обозначают буквой t, скорость - V, силу - F и пр.

Если значение величины не изменяется, то она называется по­стоянной величиной или константой. Пример константы - число Пифагора  = 3,14159  .. Величина, значение которой может меняться, называется переменной. Например, в описании процесса падения тела переменными величинами являются высота Н и время падения t.

Третьим свойством величины является ее тип. С понятием типа величины вы также встречались, знакомясь с программиро­ванием и базами данных. Тип определяет множество значений, которые может принимать величина. Основные типы величин: числовой, символьный, логический . Поскольку в данном разделе мы будем говорить лишь о количественных характеристиках, и рассматриваться будут только величины числового типа.

А теперь вернемся к примерам 1-3 (см. начало параграфа) и обозначим (поименуем) все переменные величины, зависимости между которыми нас будут интересовать. Кроме имен укажем размерности величин. Размерности определяют единицы, в кото­рых представляются значения величин.

1) t (с) - время падения; Н (м) - высота падения. Зависи­мость будем представлять, пренебрегая учетом сопротивле­ния воздуха; ускорение свободного падения g (м/с² ) будем считать константой.

2) Р (н/м2 ) - давление газа (в единицах СИ давление измеряет­ ся в ньютонах на квадратный метр); t (⁰С) - температура газа. Давление при нуле градусов Р₀ будем считать констан­той для данного газа.

3) Загрязненность воздуха будем характеризовать концентра­цией примесей (каких именно, будет сказано позже) - С (мг/м³ ). Единица измерения - масса примесей, содержа­щихся в 1 кубическом метре воздуха, выраженная в милли­граммах. Уровень заболеваемости будем характеризовать числом хронических больных астмой, приходящихся на 1000 жителей данного города - Р (бол. /тыс.).

Отметим важное качественное различие между зависимостя­ми, описанными в примерах 1 и 2 , с одной стороны, и в приме­ ре 3, с другой . В первом случае зависимость между величинами является полностью определенной: значение Н однозначно опре­деляет значение t (пример 1), значение t однозначно определяет значение Р (пример 2). Но в третьем примере зависимость между значением загрязненности воздуха и уровнем заболеваемости но­сит существенно более сложный характер; при одном и том же уровне загрязненности в разные месяцы в одном и том же городе (или в разных городах в один и тот же месяц) уровень заболевае­мости может быть разным, поскольку на него влияют и многие другие факторы. Отложим более детальное обсуждение этого при­ мера до следующего параграфа, а пока лишь отметим, что на ма­тематическом языке зависимости в примерах 1 и 2 являются функциональными, а в примере 3 - нет.

2 Математические модели

Если зависимость между величинами удается представить в математической форме, то мы имеем математическую модель.

Математическая модель - это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики.

Хорошо известны математические модели для первых двух примеров. Они отражают физические законы и представляются в виде формул:

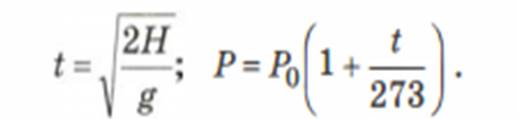
Это примеры зависимостей, представленных в функциональ­ной форме. Первую зависимость называют корневой (время про­порционально квадратному корню высоты), вторую - линейной.

В более сложных задачах математические модели представля­ются в виде уравнений или систем уравнений. В конце данной главы будет рассмотрен пример математической модели, которая выражается системой неравенств.

В еще более сложных задачах (пример 3 - одна из них) зависимости тоже можно представить в математической форме, но не функциональной , а иной.

3 Табличные и графические модели

Рассмотрим примеры двух других, не формульных, способов представления зависимостей между величинами: табличного и графического. Представьте себе, что мы решили проверить закон свободного падения тела экспериментальным путем. Эксперимент организуем следующим образом: будем бросать стальной шарик с 6-метровой высоты, 9-метровой и т. д. (через 3 метра), замеряя высоту начального положения шарика и время падения. По ре­зультатам эксперимента составим таблицу и нарисуем график (рис.3.2).

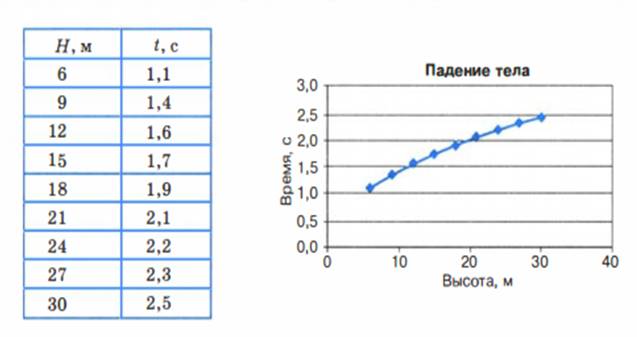
Рис. 3.2. Табличное и графическое представление зависимости времени падения тела от высоты

 Если каждую пару значений Н и t из данной таблицы подста­вить в приведенную выше формулу зависимости времени от высо­ты, то формула превратится в равенство (с точностью до погреш­ности измерений). Значит, модель работает хорошо. (Однако если сбрасывать не стальной шарик, а большой легкий мяч, то равен­ство не будет достигаться, а если надувной шарик, то значения левой и правой частей формулы будут различаться очень сильно . Как вы думаете почему?)

В этом примере мы рассмотрели три способа моделирования зависимости величин: функциональный (формула), табличный и графический. Однако математической моделью процесса падения тела на землю можно назвать только формулу. Формула бо­лее универсальна, она позволяет определить время падения тела с любой высоты, а не только для того экспериментального набора значений Н, который отображен на рис.3.2. Имея формулу, мож­но легко создать таблицу и построить график, а наоборот - весь­ма проблематично.

Точно так же тремя способами можно отобразить зависимость давления от температуры. Оба примера связаны с известными фи­зическими законами - законами природы. Знания физических законов позволяют производить точные расчеты, они лежат в основе современной техники.

Информационные модели, которые описывают развитие сис­тем во времени, имеют специальное название : динамические мо­дели. В примере 1 приведена именно такая модель. В физике ди­намические информационные модели описывают движение тел, в биологии - развитие организмов или популяций животных, в химии - протекание химических реакций и т. д.

Система основных понятий

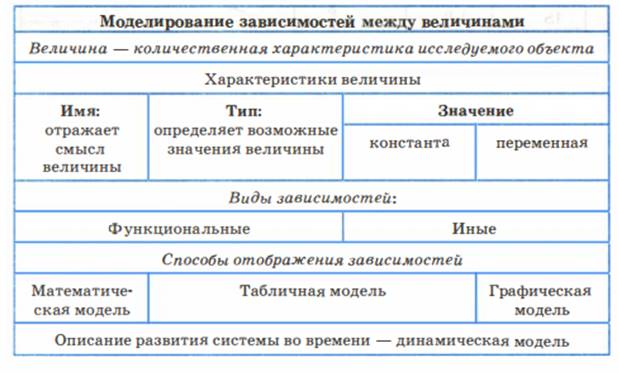
ВОПРОСЫ И ЗАДАНИЯ

1. а) Какие вам известны формы представления зависимостей между величинами?

б) Что такое математическая модель?

в) Может ли математическая модель включать в себя только константы?

2. Приведите пример известной вам функциональной зависимости (фор­мулы) между характеристиками какого-то объекта или процесса.

3. Обоснуйте  преимущества и недостатки каждой из трех форм представления зависимостей.