Лекция № 5 Представление чисел в памяти ЭВМ

Лекция № 5

Представление чисел в памяти ЭВМ

В компьютере для представления числовой информации используется двоичная система счисления. Компьютер использует две цифры, так как до сих пор не удается создать надежно работающие технические устройства, которые могли бы со стопроцентной надежностью сохранять и распознавать большее, чем два, количество различных состояний (цифр). Для двух состояний такие устройства существуют:

• электромагнитные реле (замкнуто / разомкнуто), они широко использовались в конструкциях первых ЭВМ;

• участок поверхности магнитного носителя информации (намагничен / размагничен);

• участок поверхности лазерного диска (отражает / не отражает);

• триггер может устойчиво находиться в одном из двух состояний, широко используется в оперативной памяти компьютера.

Основание в системе счисления определяет перенос в старший разряд числа. Чем меньше основание, тем быстрее растет разрядность числа. Например, одноразрядное десятичное число 5₁₀ в двоичной системе записывается с помощью трех двоичных разрядов 101₂.

Человеку очень трудно воспринимать многоразрядные числа, и поэтому он с трудом воспринимает числа, записанные в двоичном коде. Для компьютера разрядность числа не имеет большого значения, так как современные компьютеры обрабатывают за один такт работы процессора до 64 двоичных разрядов.

В процессе обработки информации на компьютере широкое распространение получили также восьмеричная и шестнадцатеричная системы счисления. Программисты часто используют эти системы на этапах отладки программ или просмотра содержимого файлов, т.к. информация представляется в этом случае в более удобной для просмотра сжатой форме (используется меньшее количество разрядов).

Целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от  00000000₂ до 11111111₂, а в двухбайтовом формате – от 00000000 00000000₂ до 11111111 11111111₂.

Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «+» кодируется нулём, а «–» - единицей.

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.

Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путём замены разнообразных арифметических операций операцией сложения. Положительные числа в прямом, обратном и дополнительных кодах изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде.

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный  или дополнительный двоичный код и в таком виде  хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.

Естественная и экспоненциальная запись числа

Числа в компьютере могут быть записаны в естественной или экспоненциальной форме. Естественной формой называется привычная нам, обычная запись чисел, например, 3,14; 2001 и т.д.

Экспоненциальная форма чисел обычно используется для записи либо очень больших, либо очень маленьких чисел, которые в обычной естественной форме содержат большое количество незначащих нулей (например, 1000000 = 1*10⁶, 0,000001 = 1*10^-5)

В языках программирования и компьютерных приложениях при записи чисел в экспоненциальной форме вместо основания системы счисления 10 пишут букву Е, вместо запятой – точку, знак умножения не ставится (например, 1000000 = 1Е6, 0,000001 = 0.1Е–5).

Число А в любой системе счисления в экспоненциальной форме записывается следующим образом:

A = m*qⁿ?

m – мантисса числа,

q – основание системы счисления

n – порядок числа.

Примеры записи целых и дробных чисел в естественной и экспоненциальной формах в десятичной и двоичной системах счисления приведены в таблице.

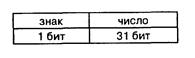
В естественной форме в компьютере хранятся в памяти и обрабатываются в процессоре целые числа. Для хранения целых положительных чисел отводится одна ячейка памяти (8 бит), для хранения целых чисел — две ячейки (16 бит), а для хранения больших целых чисел — четыре ячейки (32 бита). С учетом выделения одного разряда для знака числа для хранения больших целых чисел используется 31 двоичный разряд.

Таким образом, максимальное двоичное число равно:

Следовательно, абсолютная величина больших целых чисел не может превышать 2³¹–1, а диапазон их изменения составляет от -2 147 483 647 до 2 147 483 647.

Числа, записанные в экспоненциальной форме, являются числами с плавающей точкой. В числах с плавающей точкой арифметические операции производятся отдельно над мантиссой и порядком, например, при умножении таких чисел их мантиссы перемножаются, а порядки складываются.

Если числа обрабатываются компьютером в экспоненциальной форме, диапазон изменения величины чисел может быть гораздо больше, чем у чисел, записанных в естественной форме. Числа одинарной точности занимают четыре ячейки памяти (32 бита), а числа двойной точности — восемь ячеек (64 бита).

В случае чисел двойной точности для хранения порядка числа отводится 11 бит (из них 1 бит для знака порядка) и для хранения мантиссы числа 53 бита (из них 1 бит для знака мантиссы).

В этом случае максимальное значение порядка числа составит 1111111111₂ (1024₁₀). С учетом того, что и порядок числа, и мантисса могут принимать как положительные, так и отрицательные значения, максимальное значение числа составит 2¹⁰²⁴, а минимальное – 2^-1024.

Если перевести эти двоичные числа в десятичные (например, с использованием стандартного приложения Windows Калькулятор), то в качестве максимального числа мы получим 1,79769313486232*10³⁰⁸ а в качестве минимального - 0,556268464626800*10^-308 (количество значащих цифр десятичного числа в компьютерном представлении ограничено 15 разрядами). Мы видим, что в экспоненциальном представлении чисел в компьютере их диапазон существенно больше, чем в естественном представлении.