Лекция по математике на тему:"Равносильность уравнений, неравенств, систем"

Лекция

Тема: Равносильность уравнений, неравенств, систем

Количество часов: 2 часа

Цель: расширение понятийной базы по теме «Уравнения, неравенства, системы» за счет включения в нее новых элементов; систематизация учебного материала и выявление логики

План:

1.       Понятие о равносильности уравнений и неравенств.

2.       Понятие о равносильности систем уравнений.

Вопрос 1. Понятие о равносильности уравнений и неравенств.

Определение. Равенство с переменной называется уравнением.

В общем виде уравнение понимается как аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны.

Общий вид уравнения с одной переменной х

f(x) = g(x)

Корнем (или решением) уравнения называется значение переменной, превращающее уравнение в верное числовое равенство.

Определение. Если два выражения с переменной соединить одним из знаков: > (больше), < (меньше), >= (больше или равно), <= (меньше или равно), то получим неравенство с переменной.

Общий вид неравенства с одной переменной х (например, для случая «больше»):

f(x) >g(x)

Решением неравенства называется значение переменной, превращающее это неравенство в верное числовое неравенство.

Таким образом, решить уравнение (неравенство) – значит найти все его корни (решения) или показать, что их нет.

Определение. Областью допустимых значений (ОДЗ, или областью определения) уравнения или неравенства называется общая область определения для функций f(x) иg(x), стоящих в левой и правой частях уравнения или неравенства.

Определение. Два уравнения (неравенства) называются равносильными (или эквивалентными) на некотором множестве (обычно на ОДЗ исходного уравнения или неравенства), если на этом множестве они имеют одни и те же решения, т.е. каждое решение первого уравнения (неравенства) является решением второго и, наоборот, каждое решение второго – является решением первого.

Некоторые теоремы о равносильности

Вопрос 2. Понятие о равносильности систем уравнений.

Если ставится задача найти все общие решения двух (или больше) уравнений или неравенств с одной или несколькими переменными, то говорят, что надо решить систему уравнений или неравенств.

Определение. Решением системы называется такое значение переменной или такой упорядоченный набор значений переменных (если переменных несколько), которые удовлетворяют сразу всем уравнениям (неравенствам) системы, т.е. решением системы двух или больше уравнений (или неравенств) с n неизвестными называется такое упорядоченное множество из n чисел, при подстановке которых в систему вместо неизвестных все уравнения (или неравенства) превращаются в верные числовые равенства (или неравенства).

Решить систему уравнений или неравенств – значит найти все ее решения или доказать, что решений нет.

Если система не имеет решения, то ее называют несовместной.

Определение. Две системы уравнений (или неравенств) называются равносильными на некотором множестве, если они на этом множестве имеют одинаковые решения, т.е. каждое решение первой системы на этом множестве является решением второй и обратно, каждое решение второй является решением первой.

Как и для уравнений, все равносильные преобразования систем выполняются на ОДЗ исходной системы.

ОДЗ (областью допустимых значений) системы называется общая область определения для всех функций, которые входят в запись этой системы.

Основные утверждения о равносильности систем

(свойства равносильности систем)

1.     Если изменить порядок уравнений (или неравенств) заданной системы, то получим систему, равносильную заданной.

2.     Если одно из уравнений (или неравенств) системы заменить на равносильное ему уравнение (или неравенство), то получим систему, равносильную заданной.

3.     Если первое уравнение некоторой системы, например 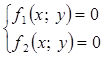, равносильно совокупности, состоящей из k уравнений то заданная система равносильна совокупности kсистем

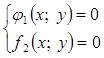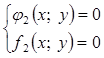 или   или …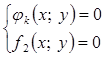

      (аналогично для систем неравенств).

4.     Если в системе уравнений из одного уравнения выразить одну переменную, например х через другие и полученное выражение подставить вместо х во все остальные уравнения системы, то получим систем, равносильную заданной.

5.     Если первое уравнение системы заменить суммой первого уравнения, умноженного на число , и второго уравнения, умноженного на число  (а все остальные уравнения оставить без изменения), то получим систему, равносильную заданной.

Вопросы для самопроверки:

1.     Дайте понятие уравнению (неравенству).

2.     Какие уравнения (неравенства) называются равносильными?

3.     Что означает понятие «система несовместна»?

4.     Когда две системы уравнений (неравенств) считаются равносильными?

Список литературы и ссылки на Интернет-ресурсы, содержащие информацию по теме:

1.        Башмаков М.И., Математика: учебник для студ. учреждений сред. проф. образования / М.И. Башмаков. –7-е изд., стер. – М с.: Издательский центр «Академия», 2020. – 256с.

2.        Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. организаций: базовый и углубл. уровни  – М.: Просвещение, 2018. – 431 с.: ил.