Лекция 2. МНОЖЕСТВА И ОТНОШЕНИЯ

Цель лекции: изучить основы теории множеств, необходимые для введения фундаментального понятия "отношение", на котором строится дальнейшее изучение реляционной модели данных. Показать связь между понятиями "отношение" и "таблица".

План лекции:

1  Основные понятия теории множеств

2  Операции над множествами

3  Декартово произведение множеств

4  Отношения

1  Основные понятия теории множеств

Понятие "множество" является первичным и неопределяемым. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Объекты любой природы (числа, люди, вещи и т. д.), составляющие множество, называют его элементами. Например, студент Иванов является элементом множества студентов IV курса, март – элементом множества месяцев в году и т.д.

Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия: 

-  должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности;

-  должно существовать правило, позволяющее отличать элементы друг от друга (это означает, что множество не может содержать двух одинаковых элементов). 

Тот факт, что элемент a принадлежит множеству А записывается так: a A, в противном случае пишем a A. Для однозначного описания некоторого множества мы будем пользоваться следующими способами:

–               перечислением всех его элементов. Например, множество A, состоящее из объектов:

a, b, c, d записывают так: A = {a, b, c, d}. Данный способ применим только для конечных множеств, число элементов которых невелико;

–               указанием общего свойства элементов, принадлежащих множеству. В этом случае в фигурных скобках записывают обозначение произвольного элемента множества, ставят вертикальную черту, а затем свойство, характеризующее в точности все элементы множества. Например, множество K натуральных чисел, меньших 5 можно записать: K= {1, 2, 3, 4} или K={х | х N  и  х < 5}.   

Множества могут быть конечными или бесконечными. Например, множество работников предприятия – конечно, а множество точек прямой – бесконечно. 

Пустым множеством называют единственное множество, не содержащее ни одного элемента (обозначается символом ). Например, это множество транзисторов, изготовленных в 1930 году.

Множества A и B считают равными, если они состоят из одних и тех же элементов (записывают A = B). Например, равны следующие множества: А={>, $, @, !} и B={!, >, @, $}. Множество B называют подмножеством множества A тогда и только тогда, когда каждый элемент B принадлежит множеству A (записывается: В А). Например, А – множество студентов вуза, В – подмножество первокурсников этого вуза.

Свойство подмножеств: если В А и А В, то А=В.

Достаточно часто для наглядного изображения множеств и операций над ними используют так называемые круги Эйлера (диаграммы Венна). На следующем рисунке показаны множества А и B такие, что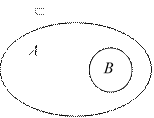 В А.

Часто бывает, что рассматриваются только подмножества одного и того же множества. Такое множество называют универсальным множеством, по предположению содержит все используемые нами множества (обозначают U и изображают на кругах Эйлера в виде прямоугольника).

2  Операции над множествами

Основными операциями над множествами являются объединение, пересечение, разность и дополнение. 

Определение 1. Объединением двух множеств называется новое множество, состоящее из элементов, принадлежащих хотя бы одному из этих множеств (обозначается: А       В ), т.е.  А      В = {х | х  А или х      В}.

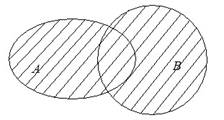
На кругах Эйлера объединение множеств А и В изображается в виде заштрихованной области.

Например, пусть заданы три множества: А = {1, 2, 3, 4}, В = {1, 3, 5}, C = {5, 6}.  Тогда А    В = {1, 2, 3, 4, 5}, А            С = {1, 2, 3, 4, 5, 6}.

Определение 2. Пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам (обозначается: А       В), т.е.  А        В = {х | х  А и х  В}.

             Например, для заданных множеств А, B и С: А     В = {1, 3}, В     С = {5}, А     С =    .

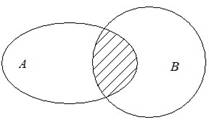
На кругах Эйлера пересечение множеств А и В изображается в виде заштрихованной области. 

Свойства операций объединения и пересечения.

а) Коммутативность: для любых множеств A и B верны равенства:

А          В=В     А; А В=В     А.

б) Ассоциативность: для любых множеств А, В, С верны равенства:

(А        В)        С=A     (В        С); (A        B)        С=A     (В        С).

в) Дистрибутивность: для любых множеств А, B и С справедливы равенства:

A          (B        C)=(A  B)        (A C); A   (B        C)=(A  B)        (A C).

В частности, для любого множества A имеем: 

A   A=A,   A   A=A;

A      =A,  A      =   ;

A   U=U,  A   U=A.

Определение 3. Разностью двух множеств А и B называется новое множество, элементы которого принадлежат A, но не принадлежат B (обозначают: А \ В), т.е. 

                                                                                А\ В = {х | х  А  и  х      В}.

На кругах Эйлера разность множеств А и В изображается в виде заштрихованной области.

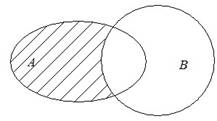
Например, для заданных множеств А, B и С: А \ В = {2, 4}, В \ С = {1, 3}, А \ С = {1, 2, 3, 4} = A.

Вопрос: каким операциям соответствует следующая диаграмма?

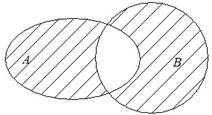
Ответ: (А \ B)    (B \ A), операция называется симметричной разностью множеств. Причем (А \ B)  (B \ A) = (А     B) \ (B             A). Доказательство этого соотношения, как и любых других утверждений о равенстве множеств, состоит в том, чтобы предположив принадлежность некоторого элемента х множеству из левой части равенства, необходимо доказать, что этот же самый элемент принадлежит множеству, стоящему в правой части равенства и наоборот.

             Задание: доказать равенство (А \ B)     (B \ A) = (А     B) \ (B     A).

Определение 4. Если А – подмножество множества U, то дополнением множества А до

множества U есть множество A, состоящее из тех и только тех элементов U, которые не принадлежат А, т.е.

                                                                          A = U \ A = {x | х  U  и  х      A}.

На кругах Эйлера дополнение изображается в виде заштрихованной области.

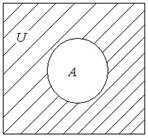
Свойства операции дополнения: для любых подмножеств А и B универсального множества U имеют место следующие равенства:

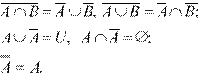
Задача. За время отпуска 12 дней шел дождь, 8 дней дул сильный ветер, а 4 дня было холодно. Сколько дней была плохая погода, если:

-  дождливых и ветреных дней было 5;

-  дождливых и холодных – 3 дня;

-  ветреных и холодных – 2 дня;

-  дождливых, ветреных и холодных – 1 день.

Ответ: 15 дней.

Задача сводится к нахождению числа элементов в объединении нескольких множеств, зная число элементов в каждом из них, а также число элементов в каждом пересечении этих множеств.

Определение 5. Количество элементов конечного множества называется его мощностью. Мощность множества А обозначается как |A|.

Мощность объединения трех множеств А, В и С равна:

             |A     B    C| = |A| + |B| 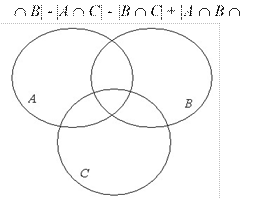+ |C| - |A        C|.

Вопрос: почему перед значением мощности пересечения трех множеств |A  B  C| стоит знак "+"?

3  Декартово произведение множеств

Пусть А и В – множества. Выражение вида (а, b), где a  A и b  B, называется упорядоченной парой. Равенство вида (a, b) = (c, d) означает, что a = c и b = d. В общем случае, можно рассматривать упорядоченную n-ку (a₁, a₂, …, a_n) из элементов a₁  A₁, a₂  A₂,

…, a_n  A_n. Упорядоченные n-ки иначе называют наборами или кортежами. 

Определение 6. Декартовым (прямым) произведением множеств A₁, A₂, …, A_n называется множество упорядоченных n-ок (наборов, кортежей) вида 

                                                         A₁  A₂  …  A_n = {(a₁, a₂, …, a_n) | a_i  A_i, i          1,n }.

Определение 7. Степенью декартового произведения A₁  A₂  …  A_n называется число множеств n, входящих в это декартово произведение. 

Если все множества A₁, A₂, …, A_n одинаковы, то используют обозначение  Aⁿ = A  A  …  A.

Примеры декартовых произведений.

а) Если А = {a, b, c, d, e, f, g, h}, а В = {1, 2, 3, 4, 5, 6, 7, 8}, то A  В = {a1, a2, a3, …, h7,

h8} – множество, содержащее обозначения всех 64 клеток шахматной доски.

б) Пусть А – конечное множество, элементами которого являются символы (буквы,

цифры, знаки препинания и т.д.). Такие множества называются алфавитами, а элементы множества Aⁿ называются словами длины n в алфавите А.

Например, множество A² = A  A содержит все возможные двухэлементные сочетания символов (слова из 2-х символов). Множество всех слов в алфавите А – это множество

Теорема. Мощность декартового произведения A₁  A₂  …  A_n равна произведению мощностей множеств A₁, A₂, …, A_n:

|A₁  A₂  …  A_n| = |A₁|  |A₂|  …  |A_n|.

Следствие: |Aⁿ| = |A|ⁿ.

4  Отношения

Пусть дано декартово произведение множеств A₁  A₂  …  A_n.

Определение 8.  Подмножество R декартового произведения множеств A₁  A₂  …  A_n называется отношением степени n (n-арным отношением) на множествах A₁, A₂, …, A_n. 

Говорят, что элементы a₁, a₂, ..., a_n находятся в отношении R, если (a₁, a₂, ..., a_n) R.

Наиболее изучены и часто используются в математике бинарные отношения. Для них, наряду с записью (a₁, a₂) R, пишут также a₁R a₂.

Например, отношение  выполняется для пар (7, 9) и (7, 7), но не выполняется для пары (9, 7). Отношение "иметь общий делитель, отличный от единицы" выполняется для пар (6, 9), (2, 4), (4, 4), но не выполняется для пар (7, 9) и (7, 7). 

Задание: для каких пар выполняются отношения "родиться в одном городе", "быть моложе", заданные на множестве S², где S – множество студентов Вашей группы?

Определение 9. Степень отношения – это количество элементов в каждом кортеже отношения.

Определение 10. Мощность отношения – это количество кортежей отношения.

Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей реляционной теории баз данных. Как будет показано ниже, отношения являются математическим аналогом таблиц. Сам термин "реляционное представление данных", впервые введенный Эдгаром Коддом в начале 1970-х, происходит от термина relation, понимаемом именно в смысле этого определения. 

Т.к. любое множество можно рассматривать как декартовое произведение степени 1, то любое подмножество можно считать отношением степени 1. Это не очень интересный пример, свидетельствующий лишь о том, что термины "отношение степени 1" и

"подмножество" являются синонимами. Нетривиальность понятия отношения проявляется, когда степень отношения больше 1. Ключевыми здесь являются два момента: 

Во-первых, все элементы отношения есть однотипные кортежи. Однотипность кортежей позволяет считать их аналогами строк в простой таблице, т.е. в такой таблице, в которой все строки состоят из одинакового числа ячеек и в соответствующих ячейках содержатся одинаковые типы данных. Например, отношение, состоящее из трех следующих кортежей {(1, "Иванов", 3), (2, "Петров", 4), (3, "Сидоров", 5)} можно считать таблицей, содержащей данные о студентах и их оценках за экзамен. Такая таблица будет иметь три строки и три колонки, причем в каждой колонке содержатся данные одного типа. Степень отношения является аналогом количества столбцов в таблице, мощность отношения – аналогом количества строк в таблице.  

Во-вторых. За исключением крайнего случая, когда отношение есть само декартово произведение, отношение включает в себя не все возможные кортежи из декартового произведения. Это значит, что для каждого отношения имеется критерий, позволяющий определить, какие кортежи входят в отношение, а какие - нет. Этот критерий, по существу, определяет для нас смысл (семантику) отношения. 

Действительно, каждому отношению можно поставить в соответствие некоторое логическое выражение P(x₁, x₂, …, x_n), зависящее от n параметров (n-местный предикат) и определяющее, будет ли кортеж (x₁, x₂, …, x_n) принадлежать отношению R. Это логическое выражение называют предикатом отношения R. Более точно, кортеж (x₁, x₂, …, x_n) принадлежит отношению R тогда и только тогда, когда предикат этого отношения P(x₁, x₂, …, x_n) принимает значение "истина". 

В математике чаще всего используют бинарные отношения (отношения степени 2). В теории баз данных основными являются отношения степени n. В математике, как правило, отношения заданы на бесконечных множествах и имеют бесконечную мощность. В базах данных напротив, мощности отношений конечны (число хранимых строк в таблицах всегда конечно). 

На следующем занятии мы рассмотрим свойства отношений и некоторые примеры отношений как бинарных, так и n-арных.