Лекция по теме "Операции над множествами "

Лекция 5-6

1.                      Универсальные множества.

2.                      Отношение множества

3.                      Дополнение множества.

4.                      Разбиения множества

5.                      Тождества алгебры множеств.

6.                      Диаграммы Эйлера-Венна.

7.                      Характеристические векторы множеств

1.Универсальные множества.

В теории множеств отдельно вводится множество, которое не содержит ни одного элемента. Такое множество называется пустым и обозначается символом

В любой конкретной задаче приходится иметь дело только с подмножествами некоторого, фиксированного для данной задачи, множества. Его принято называть универсальным (универсумом) и обозначать символом U. Например, при сборке некоторого изделия универсальным множеством естественно назвать множество всех деталей и сборочных элементов, из которых это изделие состоит. Если мы рассматриваем множества, связанные с какими-нибудь фигурами на плоскости, то в качестве универсального множества можно выбрать множество всех точек плоскости.

2.Отношения множества.

Декартово произведение множеств Пусть А и В – множества. Выражение вида (а, b), где a A и b B, называется упорядоченной парой. Равенство вида (a, b) = (c, d) означает, что a = c и b = d. В общем случае, можно рассматривать упорядоченную n-ку (a1, a2, …, an) из элементов a1 A1, a2 A2, …, an An. Упорядоченные n-ки иначе называют наборами или кортежами. Определение 6. Декартовым (прямым) произведением множеств A1, A2, …, An называется множество упорядоченных n-ок (наборов, кортежей) вида A1 A2 … An = {(a1, a2, …, an) | ai Ai , i 1,n }. Определение 7. Степенью декартового произведения A1 A2 … An называется число множеств n, входящих в это декартово произведение. Если все множества A1, A2, …, An одинаковы, то используют обозначение A n = A A … A. Примеры декартовых произведений. а) Если А = {a, b, c, d, e, f, g, h}, а В = {1, 2, 3, 4, 5, 6, 7, 8}, то A В = {a1, a2, a3, …, h7, h8} – множество, содержащее обозначения всех 64 клеток шахматной доски. б) Пусть А – конечное множество, элементами которого являются символы (буквы, цифры, знаки препинания и т.д.). Такие множества называются алфавитами, а элементы множества A n называются словами длины n в алфавите А. 6 Например, множество A 2 = A A содержит все возможные двухэлементные сочетания символов (слова из 2-х символов). Множество всех слов в алфавите А – это множество ... 1 2 A A A i i N . Теорема. Мощность декартового произведения A1 A2 … An равна произведению мощностей множеств A1, A2, …, An: |A1 A2 … An| = |A1| |A2| … |An|. Следствие: |A n | = |A| n . 4 Отношения Пусть дано декартово произведение множеств A1 A2 … An. Определение 8. Подмножество R декартового произведения множеств A1 A2 … An называется отношением степени n (n-арным отношением) на множествах A1, A2, …, An. Говорят, что элементы a1, a2, ..., an находятся в отношении R, если (a1, a2, ..., an) R. Наиболее изучены и часто используются в математике бинарные отношения. Для них, наряду с записью (a1, a2) R, пишут также a1R a2. Например, отношение выполняется для пар (7, 9) и (7, 7), но не выполняется для пары (9, 7). Отношение "иметь общий делитель, отличный от единицы" выполняется для пар (6, 9), (2, 4), (4, 4), но не выполняется для пар (7, 9) и (7, 7). Задание: для каких пар выполняются отношения "родиться в одном городе", "быть моложе", заданные на множестве S 2 , где S – множество студентов Вашей группы? Определение 9. Степень отношения – это количество элементов в каждом кортеже отношения. Определение 10. Мощность отношения – это количество кортежей отношения. Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей реляционной теории баз данных. Как будет показано ниже, отношения являются математическим аналогом таблиц. Сам термин "реляционное представление данных", впервые введенный Эдгаром Коддом в начале 1970-х, происходит от термина relation, понимаемом именно в смысле этого определения. Т.к. любое множество можно рассматривать как декартовое произведение степени 1, то любое подмножество можно считать отношением степени 1. Это не очень интересный пример, свидетельствующий лишь о том, что термины "отношение степени 1" и "подмножество" являются синонимами. Нетривиальность понятия отношения проявляется, когда степень отношения больше 1. Ключевыми здесь являются два момента: Во-первых, все элементы отношения есть однотипные кортежи. Однотипность кортежей позволяет считать их аналогами строк в простой таблице, т.е. в такой таблице, в которой все строки состоят из одинакового числа ячеек и в соответствующих ячейках содержатся одинаковые типы данных. Например, отношение, состоящее из трех следующих кортежей {(1, "Иванов", 3), (2, "Петров", 4), (3, "Сидоров", 5)} можно считать таблицей, 7 содержащей данные о студентах и их оценках за экзамен. Такая таблица будет иметь три строки и три колонки, причем в каждой колонке содержатся данные одного типа. Степень отношения является аналогом количества столбцов в таблице, мощность отношения – аналогом количества строк в таблице. Во-вторых. За исключением крайнего случая, когда отношение есть само декартово произведение, отношение включает в себя не все возможные кортежи из декартового произведения. Это значит, что для каждого отношения имеется критерий, позволяющий определить, какие кортежи входят в отношение, а какие - нет. Этот критерий, по существу, определяет для нас смысл (семантику) отношения. Действительно, каждому отношению можно поставить в соответствие некоторое логическое выражение P(x1, x2, …, xn), зависящее от n параметров (n-местный предикат) и определяющее, будет ли кортеж (x1, x2, …, xn) принадлежать отношению R. Это логическое выражение называют предикатом отношения R. Более точно, кортеж (x1, x2, …, xn) принадлежит отношению R тогда и только тогда, когда предикат этого отношения P(x1, x2, …, xn) принимает значение "истина". В математике чаще всего используют бинарные отношения (отношения степени 2). В теории баз данных основными являются отношения степени n. В математике, как правило, отношения заданы на бесконечных множествах и имеют бесконечную мощность. В базах данных напротив, мощности отношений конечны (число хранимых строк в таблицах всегда конечно)

3.Дополнение множества.

Еще одна операция, которую обычно используют при работе со множествами, это дополнение. Дополнением множестваобычно называется множество, чьи элементы не принадлежат исходному множеству. Обозначается дополнение множества A черезA. В математических обозначениях это выглядит следующим образом:  . Обычно имеет смысл говорить одополнении только в ситуации, когда имеется некоторое универсальное множество, т.е. множество, которому принадлежат все рассматриваемые элементы. Оно может зависеть от решаемой задачи. Например, в качестве такого множества может выступатьмножество натуральных чисел, множество русских букв, множество символов, обозначающих арифметические действия и т.д.

Давайте, для определенности, возьмем в качестве универсального множества множество цифр ( {0,1,2,3,4,5,6,7,8,9} ). Напишем дополнение над этим универсальным множеством.

Воспользуемся при этом очередным тождеством, которое известно в математике. А именно, тем, что A=U\A, где символ Uобозначает универсальное множество. Операция разности двух множеств у нас уже реализована.

Закодируем вышеприведенную формулу на Прологе.

supp(A,D):–

      U=[0,1,2,3,4,5,6,7,8,9],

      minus(U,A,D). /* D — это разность 

                универсального множества U

                и множества A */

Проверяем, что дополнение множества [1,2,3,4] равно множеству [0,5,6,7,8,9].

Имея дополнение, можно выразить операцию объединения через пересечение и дополнение, или, наоборот, операцию пересечениячерез объединение и дополнение, используя законы де Моргана (  и  ).

Запишем эти соотношения на Прологе.

unionI(A,B,AB):–

        supp(A,A_), /* A_ — это дополнение

                    множества A */

        supp(B,B_), /* B_ — это дополнение

                    множества B */

        intersection(A_,B_,A_B),

                 /* A_B — это пересечение

                 множеств A_ и B_ */

        supp(A_B,AB). /* AB — это дополнение

                     множества A_B */

intersectionU(A,B,AB):–

        supp(A,A_), /* A_ — это дополнение

                   множества A */

        supp(B,B_), /* B_ — это дополнение

                    множества B */

        union(A_,B_,A_B), /* A_B — это объединение

                        множеств A_ и B_ */

        supp(A_B,AB). /* AB — это дополнение

                     множества A_B */

Проверка на примерах показывает, что оба предиката работают на множествах, являющихся подмножествами универсальногомножества (в нашем примере это множество {0,1,2,3,4,5,6,7,8,9} ), как и ранее созданные предикаты union иintersection.

Мощность множества

Мощностью конечного множества называется число его элементов.

Мощность множества  X обозначается:  | X |

ПРИМЕР

  X ={1,3,6}, 

 | X | = 3

Принцип включения и исключения

Принципом включения и исключения называется формула, позволяющая вычислить мощность объединения множеств, если известны их мощности и мощности всех пересечений.

Рассмотрим частные случаи этой формулы для двух и трех множеств:

Справедливы аналогичные формулы и для пересечения множеств:

4. разбиение множества

1. Множества множеств. Мы можем рассматривать множества, состоящие из самых различных элементов. В частности, можем рассматривать множества множеств, т. е. множества, элементы которых сами суть множества. Таково, например, множество всех пар весел, имеющихся на данной лодочной станции. Множеством множеств является также множество всех спортивных команд Москвы (каждая спортивная команда есть множество составляющих ее спортсменов).

Множество всех профессиональных союзов, а также множество всех воинских частей (дивизий, полков, батальонов, рот, взводов и т. д.) данной армии являются множествами множеств. Эти примеры показывают, что множества, являющиеся элементами данного множества множеств, могут в одних случаях пересекаться, в других случаях, наоборот, не име ак, например, множество всех профессиональных союзов СССР есть множество попарно не пересекающихся множеств, так как гражданин СССР не может быть одновременно членом двух профессиональных союзов. С другой стороны, множество всех воинских частей какой-либо армии есть пример множества множеств, некоторые элементы которого являются подмножествами других элементов: так, каждый взвод естьподмножество некоторого полка, полк есть подмножество дивизии и т. д.

Множество спортивных команд данного города состоит, вообще говоря, из пересекающихся множеств, так как одно и то же лицо может входить в несколько спортивных команд (например, в команду пловцов и в команду волейболистов или лыжников).

Замечание. Для облегчения речи иногда вместо выражения «множество множеств» употребляются как совершенно равнозначащие выражения «система множеств» или «совокупность множеств».

2. Разбиение на классы. Очень важный класс систем множеств получаем, если рассматриваем всевозможные разбиения какого-нибудь множества на попарно не пересекающиеся множества. Дано множество X, представленное в виде суммы попарно не пересекающихся подмножеств; множества, слагаемые нашей суммы, и являются элементами данного разбиения множества X.

Пример 1. М есть множество всех учащихся в средних школах Москвы. Множество М можно разбить на попарно не пересекающиеся подмножества, например, следующими двумя способами:

1) мы объединяем в одно слагаемое всех учащихся одной и той же школы (т. е. разбиваем множество всех учащихся по школам);

2) мы объединяем в одно слагаемое всех учащихся одного и того же класса (хотя бы и разных школ).

Пример 2. Пусть X есть множество всех точек плоскости; возьмем на этой плоскости какую-нибудь прямую g и разобьем всю плоскость на прямые, параллельные прямой g. Множества точек каждой такой прямой и являются теми подмножествами, на которые мы разбиваем множество X.

Если данное множество X разбито на попарно не пересекающиеся подмножества, дающие в сумме множество М, то для краткости говорят просто о разбиении множества М на классы.

Теорема 3. Пусть дано отображение f множества А на множество В. Полные прообразы  всевозможных точек b множества В образуют разбиение множества А на классы. Множество этих классов находится во взаимно однозначном соответствии с множеством В.

Эта теорема, в сущности, очевидна: каждому элементу а множества А соответствует, в силу отображения, один и только один элемент  множества В, так что а входит в один полный прообраз . А это и значит, что полные прообразы точек  во-первых, дают в сумме все множество А, во-вторых, попарно  пересекаются.

Множество классов находится во взаимно однозначном соответствии с множеством В: каждому элементу b множества В соответствует класс  и каждому классу  соответствует элемент b множества В.

Теорема 4. Пусть дано разбиение множества А на классы. Это разбиение порождает отображение множества А на некоторое множество В, а именно на множество В всех классов данного разбиения. Это отображение получается, если заставить соответствовать каждому элементу множества А тот класс, к которому он принадлежит.

Доказательство теоремы уже заключено в самой ее формулировке.

Пример. Тем самым, что учащиеся Москвы распределены но школам, уже установлено отображение множества А всех учащихся на множество В всех школ: каждому учащемуся соответствует та школа, в которой он учится.

При всей самоочевидности наших двух теорем факты, устанавливаемые ими, не сразу получили в математике отчетливую формулировку; получив же эту формулировку, они приобрели очень важное значение в логическом построении различных математических дисциплин и прежде всего алгебры.

Теорема 5. Каждое разбиение на классы какого-нибудь множества X определяет между элементами множества некоторое отношение эквивалентности, обладающее свойствами симметрии, транзитивности и рефлексивности. Обратно: каждое отношение эквивалентности, установленное между элементами множества X и обладающее свойствами симметрии, транзитивности и рефлексивности, определяет разбиение множества X на классы попарно эквивалентных между собой элементов.

5.Характеристические векторы множеств

Пусть задано некоторое конечное упорядоченное множество мощности n, например, U = {1, 2, 3, 4, 5, 6, 7}, n = 7, будем считать что это универсум. Конечное множество и все его подмножества в памяти ЭВМ удобно представлять двоичным кодом (характеристическим вектором или, что то же самое, «словом» заданной длины.). Множеству U поставим в соответствие характеристический вектор «1111111», пустому множеству  Ø поставим в соответствие «0000000», множеству {2,3,5,7} – характеристический вектор «0110101». Таким образом между множеством всех подмножеств и множеством «слов» длины 7 записанных двумя символами «0» и единица установлено взаимно однозначное соответствие. Следовательно, множество всех подмножеств множества из 7 элементов равно 2⁷.

Утверждение: Если мощность конечного множества I равна | I | , то мощность множества всех его подмножеств равна 2^| I |.

Пример. А = {a, b, c}. Подмножества будут иметь вид: { Ø }, {a}, {b}, {c}, {ab}, {ac}, {bc}, {abc}, т. е. 2^|A| =2³=8.

Задачи с множествами, особенно на компьютере, удобно решать, используя характеристические векторы.

· Операция объединения подмножеств  может быть выполнена логическим сложением соответствующих элементов характеристических векторов этих подмножеств.

При объединении множеств  соответствующие элементы характеристических векторов складывают по правилу:

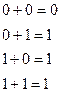
· Операция пересечения подмножеств  может быть выполнена логическим умножением соответствующих элементов характеристических векторов этих подмножеств.

При пересечении множеств  соответствующие элементы характеристических векторов считают по правилу:

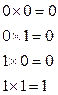
· При нахождении отрицания  нули меняют на единицы, единицы – на нули;

4) При нахождении разности  , используют формулу: 

Пример Пусть I = {1, 2, 3, 4, 5, 6}, А={1, 2, 4, 5} и В={3, 5} Характеристическим вектором множества А является вектор а : = (1, 1, 0, 1, 1, 0). Характеристический вектор множества В равен b := (0, 0, 1, 0, 1, 0).

Тогда:

Вычислим характеристический вектор множества A U  . Он равен

а или (не b) = (1, 1, 0, 1, 1, 0) или (1, 1, 0 1, 0, 1) = (1,1,0,1,1,1).

Следовательно, A U  = {1, 2, 4, 5, 6}.

· При нахождении симметричной разности А + В используют формулу: A+B=(A\B)È(B\A)

Пример Пусть I = {1, 2, 3, 4, 5, 6}, А={1, 2, 4, 5} и В={3, 5} Характеристическим вектором множества А является век­тор а : = (1, 1, 0, 1, 1, 0). Характеристический вектор множе­ства В равен b := (0, 0, 1, 0, 1, 0).

Тогда:

· Вычислим характеристический вектор множества A U В  .

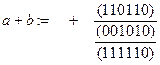 . Откуда A U В = {1, 2, 3, 4, 5}

· Вычислим характеристический вектор множества  .

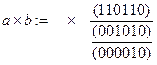 . Откуда  ={5}.

· Вычислим характеристический вектор множества  .

Век­тор а : = (1, 1, 0, 1, 1, 0).  . Тогда множество  ={ 3, 6}.

· Вычислим разность  , используем формулу:  .

Характеристический вектор множества А: а : = (1, 1, 0, 1, 1,0).

Характеристический вектор множества 

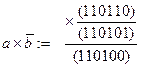 . Откуда A\ B= {1, 2, 4 }

Скачано с www.znanio.ru