Лекция. Средние арифметические показатели

Тема: Средние арифметические и их свойства.

 

1. Понятие среднего показателя

2. Виды средних величин

3. Структурные средние величины. Мода и медиана

4. Коэффициенты дифференциации и концентрации

 

 

1. Понятие среднего показателя

 

Наиболее распространённой формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина, представляющая собой обобщённую количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Средняя величина приобретает особую значимость в условиях рыночной экономики. Она помогает определить необходимое и общее, тенденцию закономерности экономического развития непосредственно через единичное и случайное. Показатель в форме средней величины выражает типичные черты однотипных явлений и дает их обобщающую характеристику по одному из варьирующих признаков. Важнейшее свойство средней величины заключается в том, что она отражает общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных единиц совокупности могут колебаться под влиянием множества факторов, среди которых могут быть как основные, так и случайные.

Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные деятельностью случайных факторов, и учитываются изменения, вызванные действием основных факторов. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Типичность средней непосредственно связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.

Английский экономист В. Петти (1623-1687 гг.) широко использовал средние величины. В. Петти хотел использовать средние величины в качестве меры стоимости расходов на среднее дневное пропитание одного работника. Устойчивость средней величины — это отражение закономерности изучаемых процессов. Он считал, что информацию можно преобразовать, даже если нет достаточного объема исходных данных.

Применял средние и относительные величины английский ученый Г. Кинг (1648-1712) при анализе данных о населении Англии.

Теоретические разработки бельгийского статистика А. Кетле (1796-1874 гг.) основаны на противоречивости природы социальных явлений — высокоустойчивых в массе, но сугубо индивидуальных. Согласно А. Кетле постоянные причины действуют одинаково на каждое изучаемое явление и делают эти явления похожими друг на друга, создают общие для всех них закономерности.

Следствием учения А. Кетле явилось выделение средних величин в качестве основного приема статистического анализа. Он говорил, что статистические средние величины представляют собой не категорию объективной действительности.

А. Кетле выразил взгляды на среднюю величину в своей теории среднего человека. Средний человек — это человек, обладающий всеми качествами в среднем размере (средняя смертность или рождаемость, средний рост и вес, средняя быстрота бега, средняя наклонность к браку и самоубийству, к добрым делам и т. д.). Для А. Кетле средний человек — это идеал человека. Несостоятельность теории среднего человека А. Кетле была доказана в русской статистической литературе в конце XIX–XX вв.

Известный русский статистик Ю. Э. Янсон (1835-1893 гг.) писал, что А. Кетле предполагает существование в природе типа среднего человека как чего-то данного, от которого жизнь отклонила средних людей данного общества и данного времени, а это приводит его к совершенно механическому взгляду и на законы движения социальной жизни: движение — это постепенное возрастание средних свойств человека, постепенное восстановление типа; следовательно, такое нивелирование всех проявлений жизни социального тела, за которым всякое поступательное движение прекращается.

Сущность данной теории нашла свое дальнейшее развитие в работах ряда теоретиков статистики как теория истинных величин. У А. Кетле были последователи — немецкий экономист и статистик В. Лексис (1837-1914 гг.), перенесший теорию истинных величин на экономические явления общественной жизни.

Его теория известна под названием теория устойчивости. Другая разновидность идеалистической теории средних величин основана на философии.

Ее основатель — английский статистик А. Боули (1869-1957 гг.) — один из самых видных теоретиков новейшего времени в области теории средних величин. Его концепция средних величин изложена в книге «Элементы статистики».

А. Боули рассматривает средние величины лишь с количественной стороны, тем самым отрывает количество от качества. Определяя значение средних величин (или «их функцию»), А. Боули выдвигает махистский принцип мышления. А. Боули писал, что функция средних величин должна выражать сложную группу с помощью немногих простых чисел. Статистические данные должны быть упрощены, сгруппированы и приведены к средним.

Эти взгляды разделяли Р. Фишер (1890-1968 гг.), Дж. Юл (1871-1951 гг.), Фредерик С. Миллс (1892 г.) и др.

В 30-е гг. XX в. и последующие годы средняя величина рассматривается как социально значимая характеристика, информативность которой зависит от однородности данных.

Виднейшие представители итальянской школы Р. Бенини (1862-1956 гг.) и К. Джини (1884-1965 гг.), считая статистику отраслью логики, расширили область применения статистической индукции, но познавательные принципы логики и статистики они связывали с природой изучаемых явлений, следуя традициям социологической трактовки статистики.

В работах К. Маркса и В. И. Ленина средним величинам отводится особая роль. К. Маркс утверждал, что в средней величине погашаются индивидуальные отклонения от общего уровня и средний уровень становится обобщающей характеристикой массового явления. Такой характеристикой массового явления средняя величина становится лишь при условии, если взято значительное число единиц и эти единицы качественно однородны. Маркс писал, чтобы находимая средняя величина была средней «…многих различных индивидуальных величин одного и того же вида».

Средние величины являются обобщающими показателями, в которых находят выражение действие общих условий, закономерность изучаемого явления.

Статистические средние величины рассчитываются на основе массовых данных статистически правильно организованного массового наблюдения. Если статистическая средняя рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений), то она будет объективной. Средняя отображает что-то общее, которое складывается в определенном единичном объекте.

Задачей средних величин является характеристика этих уровней и их изменений во времени и пространстве. Отклонение индивидуального от общего — проявление процесса развития.

 Средний показатель — это сводная характеристика, потому что формируется в нормальных, естественных, общих условиях существования конкретного массового явления, рассматриваемого в целом.

Средняя величина рассчитывается по качественно однородной совокупности, значения которой примерно одного порядка. Это - основное условие применения средней величины. Средние величины позволяют сравнивать показатели, относящиеся к совокупностям с различной численностью единиц.

Отметим, что средние величины в статистике являются величинами именованными и выражаются в тех же единицах, в которых выражен признак.

Индивидуальные значения исследуемого статистического признака у каждой единицы совокупности различны. Средняя величина индивидуальных значений одного вида — продукт необходимости, который является результатом совокупного действия всех единиц совокупности, проявляющийся в массе повторяющихся случайностей.

Одни индивидуальные явления имеют признаки, которые существуют во всех явлениях, но в разных количествах — это рост или возраст человека. Другие признаки индивидуального явления, качественно различные в различных явлениях, т. е. имеются у одних и не наблюдаются у других (мужчина не станет женщиной). Средняя величина вычисляется для признаков качественно однородных и различных только количественно, которые присущи всем явлениям в данной совокупности.

Средняя величина является отражением значений изучаемого признака и измеряется в той же размерности, что и этот признак.

Понятие средней можно раскрыть через понятие её определяющего свойства. Согласно этому понятию средняя, будучи обобщающей характеристикой всей совокупности, должна ориентироваться на определённую величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции: f(х₁, х₂, х₃ … х_n).

Данная величина в большинстве случаев отражает реальную экономическую категорию, понятие определяющего свойства средней иногда заменяют понятием определяющего показателя.

Если в приведённой выше функции все величины х₁, х₂, х₃ … х_n заменить их средней величиной  , то значение этой функции должно остаться прежним:

f(х₁, х₂, х₃ … х_n) = f().

Из данного равенства и определяется средняя величина через исходное соотношение средней (ИСС), через формулу:

ИСС =                                    (6.1)

Числитель исходного соотношения средней представляет собой её определяющий показатель. Для каждого показателя при анализе можно составить только одно истинное исходное соотношение для расчёта средней.

 

 

2. Виды средних величин

 

Метод средних используется в сочетании с методом группировок: если совокупность неоднородна, то общие средние должны быть заменены или дополнены групповыми средними, т.е. средними, рассчитанными по качественно однородным группам.

В статистической обработке материала возникают различные задачи, которые необходимо решать, и поэтому в статистической практике используются различные средние величины. В статистической практике чаще всего используются следующие виды средних величин:

• средняя арифметическая;

• средняя гармоническая;

• средняя геометрическая;

• средняя степенная (квадратическая, кубическая и т.п.).

Для того чтобы применить одну из вышеперечисленных видов средней, необходимо проанализировать изучаемую совокупность, определить материальное содержание изучаемого явления, все это делается на основе выводов, полученных из принципа осмысленности результатов при взвешивании или суммировании.

В изучении средних величин применяются следующие показатели и обозначения.

Признак, по которому находится средняя, называется осредняемым признаком и обозначается х; величина осредняемого признака у любой единицы статистической совокупности называют индивидуальным его значением, или вариантами, и обозначают как x1, х2, x3,... хп; частота — это повторяемость индивидуальных значений признака, обозначается буквой f.

 

Средняя арифметическая

Один из наиболее распространенных видов средней — средняя арифметическая простая (невзвешенная), которая исчисляется тогда, когда расчёт осуществляется по несгруппированным данным; объем осредняемого признака образуется как сумма его значений у отдельных единиц изучаемой статистической совокупности.

Для вычисления средней арифметической величины сумму всех уровней признака делят на их число.

 =                                                  (6.2)

Важно подчеркнуть, что использовать среднюю арифметическую невзвешенную можно только тогда, когда точно установлено отсутствие весов или их равенство.

Если некоторые варианты встречаются несколько раз, то сумму уровней признака можно получить умножением каждого уровня на соответствующее число единиц совокупности с последующим сложением полученных произведений, исчисленная таким образом средняя арифметическая называется средней арифметической взвешенной.

Формула средней арифметической взвешенной выглядит следующим образом:

 =                                                                (6.3)

где х_i — варианты,

f_i — частоты или веса.

Взвешенная средняя величина должна употребляться во всех случаях, когда варианты имеют различную численность.

В отдельных случаях веса могут быть представлены не абсолютными величинами, а относительными (в процентах или долях единицы). Поэтому после небольшого преобразования приведённой выше формула получим новую:

 =                                                         (6.4)

где х_i – i-й вариант рассматриваемого признака; f_i – удельный вес i-го варианта.

Арифметическая средняя как бы распределяет поровну между отдельными объектами общую величину признака, в действительности варьирующуюся у каждого из них.

При расчёте средней по интервальному вариационному ряду для выполнения необходимых вычислений используют центры интервалов. При этом величины открытых интервалов (первого и последнего) условно приравниваются к величинам, примыкавших к ним интервалов (второго и предпоследнего).

Свойства средней арифметической. Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими её сущность и в ряде случаев используемыми при её расчётах. К ним относятся следующие свойства.

1) Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие частоты (i-ой группы):

 .                                                      (6.5)

Данное свойство показывает, в каких случаях можно суммировать средние величины.

2) Сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую сторону:

Σ(х - ) = 0 = Σ(х - ) = Σх - Σ = Σх - Σn = Σх – n                                (6.6)

Это правило демонстрирует, что средняя является равнодействующей.

3) Если все варианты ряда увеличить или уменьшить на одно и тоже число α, то средняя увеличится или уменьшится на это же число α:

 = .                                                                            (6.7)

4) Если все варианты ряда увеличить или уменьшить в А раз, то средняя также увеличится или уменьшится в А раз:

 =                                                                           (6.8)

5) Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

                                                             (6.9)

Данное свойство средней показывает нам, что она не зависит от размеров весов, но зависит от соотношения между ними. В качестве весов могут быть взяты не только относительные, но и абсолютные величины.

Если все частоты ряда разделить или умножить на одно и тоже число d, то средняя не изменится.

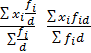 =                                                                              (6.10)

Следовательно, сумма квадратов отклонений индивидуальных значений признака от произвольной величины С больше суммы квадратов их отклонений от своей средней на величину:

Рассмотренные выше свойства средней арифметической дают возможность вывести следующие упрощенные формулы ее расчета:

а)                                                                                           (6.11)

где а – постоянная величина (условный ноль);

б)  =  • b + a                                                                             (6.12)

где b – постоянная величина.

Например, имеются три группы студентов разного роста:

Таблица 6.1. - Группы студентов

Рост (см)	160	170	180
Число студентов (чел.)	3	12	5

Тогда средний рост студента будет равен:

1) по формуле (а) условный, но равен 150:

 =  + 150 = 21 + 150 = 171;

2) по формуле (б) – условный ноль равен 150, b = 10:

 =  * 10 + 150 =171.

Средняя гармоническая. Для того чтобы определить среднюю арифметическую, необходимо иметь ряд вариантов и частот, т. е. значения х и f.

Допустим, известны индивидуальные значения признака х и произведения хf, а частоты f неизвестны, тогда, чтобы рассчитать среднюю, обозначим произведение = хf; откуда: f = m / x.

Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней.

Далее преобразуем формулу средней арифметической так, чтобы по существующим данным х и m исчислить среднюю. Выразив в формуле средней арифметической f через х и m, получим:

_{гарм.взв.} =                                                              (6.13)

Средняя в этой форме называется средней гармонической взвешенной и обозначается х гарм. взв.

Соответственно, средняя гармоническая тождественна средней арифметической. Она применима, когда неизвестны действительные веса f, а известно произведение:

fх = z                                                                    (6.14)

Когда произведения fх одинаковы или равны единицы (m = 1) применяется средняя гармоническая простая, вычисляемая по формуле:

_гарм =                                                               (6.15)

где х — отдельные варианты;

n — число.

Средняя геометрическая

Если имеется n коэффициентов роста, то формула среднего коэффициента предстает в виде формулы средней геометрической:

                              (6.16)

Средняя геометрическая равна корню степени n из произведения коэффициентов роста, характеризующих отношение величины каждого последующего периода к величине предыдущего.

Средняя квадратическая простая определяется путем извлечения квадратного корня из частного от деления суммы квадратов отдельных значений признака на их число.

                                           (6.17)

Средняя квадратическая взвешенная равна:

                                                      (6.18)

Средние объединяются в общей формуле средней степенной (при различной величине х):

                                                        (6.19)

где,  – средняя величина исследуемого явления;

х_i – i-й вариант осредняемого признака (i = 1, 2, … n);

f_i – вес i-го варианта;

k – показатель степени.

Помимо степенных средних в статистической практике используются также средние структурные, среди которых наиболее распространены мода и медиана. При осреднении уровней динамических рядов применяются различные виды средней хронологической.

Если осреднению подлежат величины, выраженные в виде квадратных функций, применяется средняя квадратическая. Например, с помощью средней квадратической можно определить диаметры труб, колес и т. д.

Что касается средней хронологической, то она рассчитывается в том случае, если имеются данные на определенные даты (обычно на начало месяца, квартала, года). Простая средняя хронологическая определяется по формуле:

                                           (6.20)

Эта формула применяется в случае наличия одинаковых интервалов между данными. Если интервалы не равны, то используется взвешенная средняя хронологическая:

 =                                                       (6.21)

где,  - средняя i-го интервала;

 – величина i-го интервала.

 

Методология расчета средней арифметической, средней геометрической, средней квадратической и средней гармонической приводятся в следующей таблице.

Таблица 6.2. – Формулы средней

Вид средней	Простые (невзвешенные) средние	Взвешенные средние
Средняя арифметическая ()
Средняя гармоническая (h) (Xгарм)
Средняя квадратическая (gn)
Средняя геометрическая (g)

В этих формулах  – значение осредняемого признака;  – соответствующие им частоты.

 

Для иллюстрации расчета средней хронологической возьмём следующие данные о численности работников предприятия и ее изменении в течение года.

Таблица 6.3. - Численности работников предприятия

Дата	Численность работников	Длительность интервала	Средняя численность в интервале	Взвешенная численность в интервале
1.01.2000	125	2 мес.	121,0	242,0
1.03.2000	117	4 мес.	123,5	530,0
1.07.2000	148	3 мес.	144,5	433,5
1.10.2000	141	3 мес.	139,0	417,0
1.01.2001	137	-	-	-

 

Поскольку интервалы не равны, расчет средней хронологической проводится по взвешенной формуле:

 =  =  =  = 135,2

 

При расчете средних величин необходимо принимать во внимание правило мажорантности средних величин. Оно заключается в том, что существуют следующие обязательные соотношения между средними величинами:

_g ≥  ≥ _g ≥ _h                                                 (6.22)

Это правило дает возможность контролировать расчеты средних величин.

 

 

 

 

 

3. Структурные средние величины. Мода и медиана

 

Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана.

Мода (Мо) — значение признаков наиболее часто встречающихся в совокупности (вариант, имеющий наибольшую частоту) или типичное значение.

Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений.

В дискретном ряду мода — это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность).

В пределах интервала надо найти то значение признака, которое является модой:

М₀ = Х₀ + h •                                        (6.23)

где хо — нижняя граница модального интервала;

h — величина модального интервала;

fm — частота модального интервала;

fm–1 — частота интервала, предшествующего модальному;

fm+1 — частота интервала, следующего за модальным.

Мода зависит от величины групп, от точного положения границ групп.

Мода применяется для решения ряда практических задач. Так, мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен, при изучении товарооборота рынка берется модальная цена, для изучения спроса на обувь, одежду используют модальные размеры обуви и одежды и др.

Медиана (Me) — это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая — большие.

Медиана — это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Или медиана – величина признака единицы совокупности находящиеся в середине ранжированного ряда.

К медиане примыкают аналогичные показатели - квартили, квинтили, десили, персили. Квартили делят совокупность на четыре равные части по 25%; квинтили – на пять равных частей по 20%; десили – на десять равных частей по 10%; персили – на 100 равных частей по 1% каждая.

Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины.

Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних.

Медиана таким образом делит ряд на две равные (по числу единиц) части — со значениями признака меньше медианы и со значениями признака больше медианы.

В ранжированных рядах несгруппированных данных нахождение медианы сводится к отысканию порядкового номера медианы, который для нечетного объема вычисляется как:

N_Ме =                                                          (6.24)

где n – число членов ряда.

 

Для четного числа единиц ряда медиана находится как средняя арифметическая двух значений, находящихся в середине ряда.

Порядок нахождения медианы, в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал. Значение медианы вычисляется линейной интерполяцией по формуле:

М_е =                                                        (6.25)

где х_ме — нижняя граница медианного интервала;

i_ме — величина медианного интервала;

f/2 — полусумма частот ряда;

S_ме – 1 — сумма накопленных частот, предшествующих медианному интервалу;

f_ме — частота медианного интервала.

или

                                     (6.26)

где х₀ – нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); i – ширина медианного интервала;  – накопленная частота интервала, предшествующего медианному;  -  частота i-го интервала, i = 1, 2, … k;  – частота медианного интервала.

Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности.

При определение моду и медианы дискретного (прерывного) признака их значения определяются либо визуальным путем для моды (выбирается значением признака, имеющее наибольшую частоту), либо отысканием значения признака, который имеет центральный член совокупности. Например, имеются следующие данные о численности работников предприятий.

Таблица 6.4. - Численности работников предприятий

Число работников	5	7	10	12	15	20
Число хозяйств	6	8	14	23	17	32

В этом случае мода равна 20 (с частотой 32), а медиана 12 (так как номера 50 и 51 совокупности имеют значение признака, равное 12). Соответственно первая квартиль равна 10 (это значение  имеют номера 25 и 26); четвертая квентиль равна 20 (это значение имеют номера 80 и 81); десиль равна 10 (поскольку номера 15 и 16 совокупности равны 10); 73-я персиль равна 20 (так как номера 73 и 74 равны 20).

Что касается медианы, квартилей, квитилей, десилей и персентилей, то они определяются по однородным формулам следующего вида:

х₀ + i                                                    (6.27)

где х₀ - нижняя граница интервала, в котором находится определяемый показатель;

i – величина этого интервала (х₁ – х₀);

f_i – частота этого интервала;

m – доля единиц совокупности, отделяемая искомым показателем (05 для медианы; 04 для второй квантили; 08 для восьмой десили и т.п.);

∑ – общее число единиц совокупности;

 – накопленные частоты всех интервалов, предыдущих по отношению к данному интервалу.

 

Например.

Таблица 6.5. - Данные об урожайности зерновых (ц/га).

Урожайность	12-14	14-16	16-18	18-20	20-22	22-24	24-26
Уборочная площадь	7	15	23	25	12	10	8

В этом случае:

1) М₀ = 18 + (20 – 18) •  = 18,2667 ц/га.

2) М_е = 18 + (20 – 18) •  = 18,4 ц/га;

3) первая квартиль = 16 + (18 – 16) •  = 16,26 ц/га;

4) третья квартиль = 18 + (20 – 18) •  = 19,2 ц/га

5) седьмая десиль = 20 (общая точка двух интервалов);

6) 43-й персентиль = 16 + (18 – 16) •  = 17,83 ц/га.

Экономический смысл полученный результатов заключается в следующем:

1) наибольшая часть уборочных площадей имеет урожайность 19,27 ц/га.

2) половина посевных площадей имеет урожайность свыше 18,4 ц/га, а другая половина – меньше 18,4 ц/га;

3) 25% посевных площадей имеет урожайность ниже 16,26 ц/га и 75% посевных площадей – свыше 16,26 ц/га;

4) 60% площадей имеют урожайность менее 19,2 ц/га и 40% площадей – свыше 19,2 ц/га;

5) 70% площадей имеют урожайность менее 20 ц/га и 30% площадей – свыше 20 ц/га;

6) 43% площадей имеют урожайность менее 17,83 ц/га и 57% площадей – свыше 17,83 ц/га.

В заключении необходимо отметить, что если средняя арифметическая совпадает по величине с модой и медианой, то такое распределение называется идеальным. В экономике такое распределение встречается крайне редко.

 

Пример расчета моды.

 

Таблица 6.6. - Распределение населения Российской Федерации по уровню среднедушевых номинальных денежных доходов в I полугодии 2007 г.

 

1. Определяем модальный интервал, это 400 – 600 тыс. руб.

2. Определяем нижнюю границу модельного интервала х₀ она равна 400 тыс. руб.

3. Определяем величину модального интервала i она равна 200 тыс. руб.

4. По зависимости (12) рассчитываем моду.

М_о = 400 + 200 ((30,6 – 29,6) / (30,6 – 25,1)) = 430,8 тыс. руб.

 

Пример расчета медианы.

1. Определяем медианный интервал, для чего рассчитываем накопленную частоту каждого последующего интервала до тех пор, пока она не превысит половину суммы накопленных частот (для нашего примера это 147,5 / 273,75 млн. чел.).

Таблица 6.7. - Определение медианного интервала

Интервал, тыс. руб.	Накопленная частота, млн. чел.
До 400	29,6
400 - 600	60,2
600 - 800	85,3

Тогда медианный интервал равен 600 – 800 тыс. руб.

2. Определяем нижнюю границу медианного интервала х₀, она равна 600 тыс. руб.

3. Определяем величину медианного интервала i, она равна 200 руб.

4. По зависимости (13) рассчитываем медиану: М_е = 600 + 200((73,75 – 60,2) / 25,1) = 708,0 тыс. руб.

 

 

4. Коэффициенты дифференциации и концентрации

 

Когда возникает потребность проанализировать структуру статистического ряда более подробно, вычисляют квартили, квинтили, децили.

Квартили делят распределение признака на четыре части. Обозначим значения x_i, делящие вариационный ряд на четыре равные части, через Q₁,Q₂, Q₃. Ниже первой квартили лежат ¼ значений x_i, ¾ элементов совокупности имеют значения x_i превышающее Q₁ (нижнюю квартиль). Вторая квартиль делит распределение пополам и совпадает с медианой, которую называют центральной квартилью. Между медианой и третьей квартилью Q₃ (верхней квартилью) располагается ¼ всей совокупности и ¼ значений лежит выше Q₃.

Квинтили делят распределение на пять равных частей. Дециль делит распределение на десять равных частей.

Первая дециль определяется по формуле:

d_i = x_k-1 + i_k                                              (8.28)

где хк-1 – нижняя граница интервала, содержащего первую дециль; ik – величина интервала, содержащего первую дециль; Fk-1 – накопленные частоты до первого децильного интервала.

Аналогично определяют девятую дециль. При изучении дифференциации широко используют децильный коэффициент – отношение девятой децили к первой. Так сравнивая девятую и первую дециль в распределении населения по уровню доходов, измеряют соотношение уровней доходов 10% наиболее обеспеченного населения и 10% наименее обеспеченного населения (в разах).

Более точно уровень дифференциации можно измерить, используя фондовый коэффициент:

K_F =                                                            (6.29)

где  - сумма значений девятой децили;  - сумма значений первой децили.

К показателям дифференциации близки по значению показатели концентрации: коэффициент концентрации Джини, коэффициент Герфиндаля, коэффициент Розенблюта.

Коэффициент концентрации Джини:

G =                                      (6.30)

где p_i – накопленная доля (частость) численности единиц совокупности; q_i – накопленная доля значений изучаемого признака.

Коэффициент Джини принимает значение от 0 до 1, при этом, чем ниже показатель, тем более равномерно распределение.

Индекс Герфиндаля-Гиршмана (HHI) рассчитывается как сумма квадратов рыночных долей конкурентов, действующих на определенном сек- торе рынка:

HHI =                                                (6.31)

где S_i – доля i-той фирмы на рынке одноименных товаров (ее доля в общем объеме реализации названных товаров); n – общее число предпринимательских фирм на данном секторе рынка.

Чем меньше коэффициент HHI, тем, соответственно, слабее конкурентная позиция отдельных субъектов предпринимательского бизнеса на рассматриваемом секторе рынка. Основное достоинство коэффициента Герфиндаля-Гиршмана – его высокая чувствительность к изменению в суммарном обороте долей крупнейших участников, что позволяет отслеживать концентрацию рыночного оборота. Низко концентрированным является рынок при HHI < 800, умеренно концентрированным является рынок при HHI > 800, высококонцентрированным является рынок при HHI > 1800.

Важно и то, что коэффициент реагирует на число участников рынка. Однако его крупнейшим участникам придается наибольший вес, вследствие этого существует опасность преувеличений уровня концентрации. Поэтому наряду с коэффициентом HHI целесообразно применять коэффициент Розенблюта, который рассчитывается на основе сопоставления рангов предпринимательских фирм на рынке одноименных товаров и долей этих фирм на рассматриваемых рынках, при этом наибольший ранг имеют фирмы с наименьшими долями:

K_R =                                                      (6.32)

где R_i – ранг i–той фирмы на рынке одноименных товаров (по убывающей, самая крупная фирма имеет ранг 1); j_i – доля продаж i-той фирмы на рынке одноименных товаров; n – количество участников рынка.

Коэффициент Розенблюта принимает значение от 0 до 1. Чем меньшим в результате вычислений оказывается значение этого индекса, тем менее монополизированным выглядит искомый сектор. Максимальное значение равно 1; в этом случае есть все основания сделать вывод о том, что один из субъектов бизнеса, представленный на рассматриваемом секторе рынка, приобрел монопольную позицию. В целом коэффициент Розенблюта имеет тенденцию преуменьшать концентрацию в совокупности.