Лекция Статистические таблиц и графики

Тема 4. Статистические таблицы и графики

 

1. Статистические таблицы

2. Статистические графики

 

 

4. Статистические таблицы

 

Статистическая таблица – это цифровое выражение итоговой характеристики всей наблюдаемой совокупности или ее составных частей по одному или нескольким существенным признакам, взаимосвязанным логикой экономического анализа.

Таким образом, статистическая таблица является средством наглядного выражения результатов исследования. Значение таблицы определяется тем, что они позволяют исследовательские статистические данные рассматривать совместно, достаточно полно и точно охватывая сложную природу явления. Любая статистическая таблица представляет собой форму рационального, наглядного изложения статистических данных о явлениях и процессах, изучаемых статистикой.

Прежде чем переходить к рассмотрению видов и правил построения статистических таблиц, необходимо иметь представление об основных элементах, её формирующих.

Если из статистической таблицы изъять все слова и цифры, то получится графленая сетка. Вертикальные столбца ее называют графами, а горизонтальные строками. Следовательно, внешне таблица представляет собой перечень граф и строк. Если записать заголовки графи и строк – это будет макет таблицы (рис. 4.1.)

Составление макета таблицы – важное направление обработки статистических материалов. Для того чтобы получилась полная таблица, достаточно внести данные статистической сводки в пересечение каждой строки и граф.

 

Подлежащее ↓ Содержание строк	Сказуемое Наименования граф (верхние заголовки)
А	1	2	3	4
Наименования строк (нижние заголовки)
……………………
……………………
Итоговая строка

Рисунок 4.1. Макет статистической таблицы

 

Статистическая таблица, является экономическим предложением, в котором существуют: подлежащее и сказуемое. Подлежащее таблицы – это перечень единиц совокупности или группы, составляющих исследуемую совокупность единиц наблюдения (т.е. объект изучения). Сказуемым таблицы являются числовые показатели, данные, характеризующие изучаемый объект (подлежащее). Обычно, подлежащее располагается в виде названия строк, сказуемое – сверху в виде названия граф. Однако в случае необходимости для более полного и удобного способа прочтения и анализа исходной информации расположение подлежащего и сказуемого может меняться местами.

По построению подлежащего таблицы могут быть:

- простыми;

- групповыми;

- комбинационными.

Простой называется такая статистическая таблица, в подлежащем которой содержится перечень рассматриваемых объектов. При этом части подлежащего не являются группами одинакового качества, отсутствует систематизация изучаемых единиц.

Таблица 4.1. Типология поведения потребителей новых товаров

Категории потребителей	%, к итогу
Новаторы (модники)	3
Ранние последователи	14
Раннее большинство	32
Отсталое большинство	36
Консерваторы	15
Всего	100

 

Простые таблицы бывают:

- перечневые – подлежащее – перечень едини, составляющих объект изучения;

- территориальные – дается перечень территорий, стран, областей, городов и др.;

- хронологические – в подлежащем приводятся периоды времени и даты.

Групповыми называются таблицы, в подлежащем которых изучаемый объект разделен на группы по какому-либо признаку, при этом каждая группа характеризуется рядом показателей (таблица 4.2). Иначе говоря, групповые таблицы возникают в результате применения метода группировок при сводке статистических данных.

 

Таблица 4.2. Распределение трудоустроенных по полу и длительностью перерыва в работе

Пол	Длительность перерыва в работе, мес.
	1	2	3	4	5
Мужчины	4	6	4	-	4
Женщины	-	3	4	3	0
Всего	4	9	8	3	3

 

Часто в сказуемом групповых таблиц показатели располагаются по периодам, т.к. в изменении соотношения групп во времени проявляется определённая закономерность.

 

Комбинационной таблицей называется такая, где в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации (таблица 4.3). Познавательная сторона комбинационных таблиц заключается в том, что появляется возможность проследить влияние на признаки сказуемого не одного, а двух и более факторов, т. е. признаков, которые легли в основу комбинационной группировки.

 

Таблица 4.3. Влияние качества почв и удельного веса сортовых посевов на урожайность зерновых культур.

Группы хозяйств по качеству почв	Подгруппы хозяйств по удельному весу сортовых посевов, пшеницы %	Число хозяйств	Посевная урожайность, ц/га площадь зерновых, тыс. га		Валовой сбор зерна, т	Урожайность, ц/га
I – лучшие	До 70 70 и более	1 4	3,6 2,8		7200	20,0
	Итого по I гр.	5	3,4
II – средние	До 70 70 и более	4 10		2,6 2,7	4500	15,0
	Итого по II гр.	14		2,2
III – худшие*	До 70 70 и более	9 2		2,1 2,8	2900	22,0
	Итого по III гр.	11		2,0
Всего		30

 

Наряду с подлежащим важным элементом статистической таблицы является сказуемое.

Виды таблиц по характеру сказуемого. Система показателей, которыми характеризуется подлежащее как объект изучения, образуют статистические таблицы.

Таблицы по структуре сказуемого различают с простой и сложной разработкой.

Простыми называются такие статистические таблицы, в подлежащем которых нет группировки, а дается перечисление территориальных единиц, единиц времени или какой-либо другой перечень, показатели, характеризующие подлежащее таблицы располагаются параллельно друг другу (таблица 4.4).

Таблица 4.4. Динамика зависимости стран от импорта первичных энергоресурсов.

Страна	Потребление энергоресурсов		Производство энергоресурсов
	1980	1995	1980	1995
А	188	374	176	160
В	254	302	228	199
С	117	231	73	45
D	52	156	26	31

 

Простые таблицы имеют самое широкое распространение. Статистический анализ простой таблицы ограничивается параллельным сравнением приведенных показателей сказуемого. Более глубокий анализ простой таблицы невозможен в силу отсутствия причинной связи между показателями подлежащего и сказуемого. Комбинация признаков сказуемого не дает основания для отнесения простых таблиц к комбинированным, так как такая комбинация все равно не позволяет исследовать зависимость между признаками.

Простая разработка сказуемого предусматривает параллельное расположение показателей, а сложная – комбинированное. Например, при простой разработке сказуемого могут быть сначала приведены графов, содержащие данные о распределении населения по полу или по уровню образования. При сложной разработке сказуемого – в каждой графе по уровню образования приводятся данные о численности мужчин, женщин и итоговые в виде отдельных граф (в макете таблицы это графы 3, 4, 5) (таблица 4.5).

 

Таблица 4.5. - Статистическая таблица со сложной комбинированной разработкой сказуемого

№ рынка	Средняя цена, руб.	Продано, тыс. кг		Удельный вес продажи, %
		Март	Май	Март	Май
1	3,5	35	28	25	20
2	3,0	42	42	30	30
3	2,5	63	70	45	50

 

Практикой выработаны определённые требования к составлению и оформлению таблиц.

1. Таблица по возможности должна быть компактной, краткой и небольшой по размеру. Не следует загружать ее излишними подробностями, затрудняющими анализ исследуемых явлений. Иногда целесообразнее построить две-три небольших таблицы, чем одну большую. Краткую таблицу легче анализировать. Цифровой материал необходимо располагать так, чтобы при анализе таблицы сущность явления раскрывалась чтением строк слева направо и сверху вниз.

2. Каждая таблица должна иметь подробное название, из которого становится известно: а) какой круг вопросов излагает и иллюстрирует таблица; б) каковы географические границы статистической совокупности, представленные таблицей; в) каков период времени, за который приведены данные, или момент времени, к которому они относятся; г) каковы единицы измерения (если они одинаковы для всех табличных клеток). Если единицы измерения неодинаковы, то в верхних или боковых заголовках обязательно следует указывать, в каких единицах приводятся статистические данные (тонн, штук, рублей и пр.)

3. Заголовки таблицы, названия граф и строк должны быть чёткими, краткими, лаконичными, представлять собой законченное целое, вписываться в содержание текста, избегать большого количества запятых, токи только при сокращениях.

4. В таблице желательно давать нумерацию граф. Это облегчает пользование таблицей, дает возможность лучше ориентироваться, показывает способ расчета цифр в графах. Первые графы, содержащие подлежащее, обозначаются заглавными буквами алфавита; графы, содержащие сказуемое, нумеруются арабскими цифрами. Заглавия срок подлежащего и граф сказуемого должны быть сформулированы, кратко, точно и ясно. Все слова в заголовках подлежащего и сказуемого таблицы записываются по возможности полностью. Заголовки граф следует сформулировать так, чтобы были ясны смысл данной величины и порядок ее расчета.

5. Приводимые в подлежащем и сказуемом признаки должны быть расположены в логическом порядке с учетом необходимости рассматривать их совместно. Обычный принцип размещения – от частного к общему, т.е. сначала показывают слагаемые, а в конце подводят итоги (если это необходимо). Когда приводятся не все слагаемые, а лишь наиболее важные из них, применяется противоположный принцип – сначала показывают общие итоги, а затем выделяют наиболее важные части («В том числе», «Из них»). Следует различать «Итого» и «Всего». «Итого» является итогом для определенной части совокупности, а «Всего» - итог для совокупности в целом.

6. Информация, располагаемая в графах таблицы, обычно завершается итоговой строкой «Итого» или «Всего», «В том числе».

7. Если названия отдельных граф повторяются между собой, содержат повторяющиеся термины или несут единую смысловую нагрузку, то им необходимо присвоить общий объединяющий заголовок. Данный приём используется как для подлежащего, так и для сказуемого таблиц.

8. Взаимосвязанные и взаимозависимые данные, характеризующие одну из сторон анализируемого явления, необходимо располагать в соседних друг с другом графах.

9. Графы и строки должны содержать единицы измерения, соответствующие поставленным в подлежащем и сказуемом показателям. Используются общепринятые сокращения. Если все графы имеют единую единицу измерения, то она выносится в заголовок таблицы.

10. Для удобной работы с цифровым материалом в таблицах числа следует расставлять в середине граф, одно под другим: единицы под единицами, запятые под запятыми. Чётко соблюдая разрядность.

11. Числа по возможности целесообразно округлять с одинаковой степенью точности (до 0,2; до 0,01 и т.п.). Если в таблице приводятся проценты роста, то во многих случаях целесообразно проценты от 300 и более заменять отношениями в разах. Например, писать не 1000%, а «в 10,0 раз».

12. Таблица может сопровождаться примечаниями, в которых указываются источники данных, более подробно раскрывается содержание показателей, даются и другие пояснения, а также оговорки в случае, если в таблице содержит данные, полученные в результате вычислений.

13. При оформлении таблиц обычно применяются такие условные обозначения:

знак тире (-) – когда явление отсутствует;

х – если явление не имеет осмысленного содержания;

многоточие (…) – когда отсутствуют сведения о его размере (иди делается запись «Нет сведений»). Если сведения имеются, но числовое значение меньше принятой в таблице точности, оно выражается дробным числом (0,0).

Прежде чем приступить к анализу её данных, необходимо ознакомиться с названием таблицы, заголовками граф и строк, установить, к какому периоду или на какую дату, к какой территории относятся данные, обратить внимание на единицы измерения, понять, какие процессы характеризуются средними и относительными величинами.

Анализ статистической таблицы следует начинать с итогов. Ознакомление с ними даёт общее представление о содержании таблицы. Далее переходим к изучению отдельных строк и граф. Но читать их нужно не подряд, а выбирать сначала частные итоги и наиболее характерные данные, затем анализировать все остальное.

 

 

2. Статистические графики

 

Современную науку невозможно представить себе без применения графических методов, настолько прочно вошли они в арсенал средств научного общения и в методику научного исследования. Графические методы помогают прежде всего описанию, а затем и анализу этих данных. С помощью графиков легко выявить и наглядно представить закономерности, которые часто трудно бывает уловить в сложных статистически таблицах.

Ряды распределения удобно анализировать при помощи их графического изображения, позволяющего судить и о форме распределения. При этом используются различные графики, многообразие видов которых обусловлено различиями в их статистическом содержании, способах построения и широтой круга изображаемых ими общественных явлений и процессов. Графическое представление статистических данных помогает легко выявить пики и спады, явно не соответствующие изображаемым статистическим данным, аномалии и отклонения.

Графическое представление статистических данных является не только средством иллюстрации статистических данных и контроля их правильности, но и их достоверности. Графики незаменимы при одновременном изучении нескольких взаимосвязанных экономических явлений, так как позволяет с первого взгляда установить существующие между ними соотношения и связи, различие и подобие, выявить особенности их изменений во времени.

Для наглядного предоставления статистической информации широко используют графики различных видов.

Статистический график – это чертёж, на котором статистические совокупности, характеризуемые определёнными показателями, описываются с помощью условных геометрических образов или знаков. Или, условные изображения числовых величин и их соотношений в виде различных геометрических фигур в системе прямоугольных координат.

С помощью графического изображения возможны изучения закономерностей развития, установление существующих взаимосвязей, выявление причинных связей.

Применение графиков позволяет облегчить их восприятие, а во многих случаях помогает уяснить сущность изучаемого явления, его закономерности и особенности, увидеть тенденции его развития, взаимосвязь характеризующих его показатели

Каждый график состоит из графического образа и вспомогательных элементов.

Графический образ – это совокупность точек, линий и фигур, с помощью которых изображаются статистические данные. Эти знаки образуют собственно языковую ткань графика, его основу.

Вспомогательными элементами графика являются:

1) поле графика то пространство, в котором размещаются образующие график геометрические знаки. Поле графика характеризуется его форматом, т.е. размером и пропорциями (соотношением сторон);

2) пространственные ориентиры, определяющие расположение геометрических знаков в поле графика. Пространственные ориентиры задаются системой координатных сеток или контурных линий, которые делят это поле на части. В большинстве случаев в статистических графиках применяется система прямоугольных (декартовых) координат, но нередко встречаются и круговые графики, построенные по принципу полярных координат;

3) масштабные ориентиры, придающие геометрическим знакам количественную определенность. Масштабные ориентиры определяются системой масштабных шкал или специальными масштабными знаками. Масштабные шкалы применяются в координатных статистических графиках. Эти шкалы представляют собой геометрическое место помеченных точек, а носителями их являются оси координат, на которых эти отметки располагаются. Масштабные знаки используются преимущественно для статистических карт;

Масштаб статистического графика – это мера перевода числовой величины в графическую. Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике и включает три элемента: линию (или носитель шкалы); определенное число точек, расположенных на носителе шкалы в определенном порядке; цифровое обозначение чисел, соответствующих отдельным точкам. Числовое значение необходимо помещать строго против соответствующих точек (рис 4.2).

Предел шкалы                                                             Предел шкалы

                →          5      10      15      20       25     ←

                              |         |         |          |          |

 

                               графические интервалы

                                 длина шкалы

Рисунок 4.2. - Числовые интервалы

 

Масштаб шкалы – это длина отрезка (графический интервал), принятого за единицу и измеренного в каких-либо мерах. Построить шкалы – значит, на заданном носителе шкалы разместить точки их соответствующими числами согласно по изображённым данным.

4) экспликация графика состоит из объяснения: название графика, которое в краткой форме передаёт его содержание; подписи вдоль масштабных шкал и пояснения к отдельным частям графика; легенду графика, которая даётся вне поля графика и содержит пояснения графических образов.

Без экспликации график трудно прочитать и понять. Название графика должно кратко и точно раскрывать его содержание. Пояснительные тексты могут располагаться в пределах графического образа или рядом с ним (ярлыки). А также выноситься за его пределы (ключ).

Статистические графики классифицируют по ряду признаков: назначению (содержанию), способу построения и характеру графического образа.

По способу построения графики делятся на диаграммы и статистические карты (картограммы картодиаграммы). Диаграммы используются для наглядного изображения количественных величин в различных аспектах (во времени и пространстве). Они делятся на диаграммы сравнения, диаграммы динамики и структурные диаграммы.

Диаграммы сравнения служат для сопоставления количественной величины однородных явлений в пространстве (например, диаграммы численности населения России, США и Китая).

Диаграммы динамики отражают изменение изучаемого показателя во времени (например, диаграмма численности населения России с 1980 по 2000 гг.).

Структурные диаграммы характеризуют изменение структуры изучаемого явления (т.е. доли отдельных компонентов в изучаемом явлении и их динамику).

По форме графического изображения статистические графики делятся на линейные, плоскостные и объемные. В линейных диаграммах средством наглядного изображения изучаемого явления служат прямые, ломанные и кривые линии. Прямые линии в статистической практике встречаются очень редко – в тех случаях, когда изучаемое явление за равные промежутки времени уменьшаются на одну и ту же постоянную величину.

В подавляющем большинстве случаев в линейных графиках используются ломаные линии, т.к. обычно явления развиваются не равномерно.

По содержанию или назначению можно выделить графики сравнения в пространстве, графики различных относительных величин (структуры, динамики и т.п.), графики вариационных рядов, графики размещения по территории, графики взаимосвязанных показателей. возможны и комбинации этих графиков, например графическое изображение вариации в динамике или динамики взаимосвязанных показателей и т.п.

По способу построения графики можно разделить на диаграммы, картодиаграммы и картограммы.

По характеру графического образа различают графики точечные, линейные, плоскостные (столбиковые, почасовые, квадратные, круговые, секторные, фигурные) и объемные.

Линейные диаграммы – широко используются для характеристики изменения явлений во времени, изучения рядов распределения связи между явлениями, выполнения плановых заданий. Линейные диаграммы строятся на координатной сетке. Геометрическими знаками в линейных диаграммах служат точки и последовательно соединяющие их отрезки прямой, которые складываются в ломанные кривые.

Ось абсцисс является осью времени с равномерно размещенными отметками, а ось ординат – осью значений, которые принимает с течением времени изучаемый показатель. По отметкам обеих шкал определяют местоположение точек в координатном поле диаграммы, а последовательно их, соединяя, находят кривую динамики изображаемого на диаграмме показателя. Конфигурация каждой кривой на динамической диаграмме отражает процесс изменения во времени описываемого на диаграмме показателя, а именно: движение кривой с ходом времени вправо и вверх означает рост показателя, а движение ее вправо вниз – его падение.

На одной линейной диаграмме могут строиться несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя для различных территорий. Пример построения таких кривых представлен на рис.

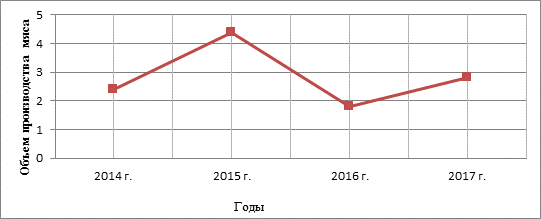
Рисунок 4.2. Объём производства мяса

Таким образом, кривая, проведенная в координатном поле динамической диаграммы, в большей мере, чем другие знаки-символы статистических диаграмм, обусловлена содержательным смыслом отражаемого явления.

Для изображения вариационных рядов применяются линейные и плоскостные диаграммы, построенные в прямоугольной системе координат. При дисконтной вариации признака графика вариационного ряда служит полигон распределения. При его построении на оси абсцисс откладываются значения варьирующего признака, а на оси ординат – абсолютные численности (частоты)

Полигон распределения представляет собой замкнутый многоугольник, абсциссами вершин которого являются значения варьирующего признака, а ординатами – соответствующие им частотами (рис. 4.3).

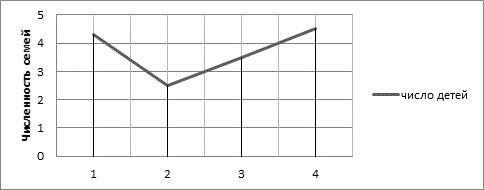
Рисунок 4.3. – Распределение семей по числу детей

 

При непрерывной вариации используют интервальные вариационные ряды, графическим изображением которых служит гистограмма. Гистограмма распределения применяется чаще всего для изображения интервальных рядов.

Для построения гистограммы по оси абсцисс в соответствии с принятым масштабом откладывают интервалы признака, а по оси ординат – численность единиц совокупности. на отрезках изображающих интервалы, стоят прямоугольники, площади которых пропорциональны численностям единиц Эти интервалы являются основаниями прямоугольников, площади которых равны либо пропорциональны частотам или частностям распределения в соответствующих интервалах (рис. 4.4).

 

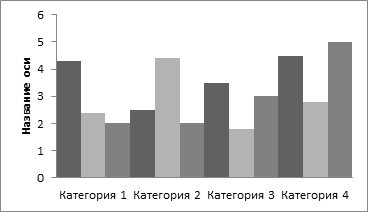
Рисунок 4.4. - Гистограмма

Как известно, плотность распределения – это число единиц совокупности, приходящееся на единицу ширины интервала. При равных интервалах плотность распределения прямо пропорциональна частотам или частностям, которые и используются для построения прямоугольников. При неравных интервалах гистограмма строится только по плотности распределения.

Для иллюстрации рядов распределения используются также кумуляты и огивы. Для их построения на оси абсцисс отмечаются значения дискретного признака (или концы интервалов), а на оси ординат – нарастающие итоги частот (кумулята) или частностей (огива), соответствующих этим значениям признака.

Ордината кумулятивного графика показывает, сколько единиц или какая часть совокупности имеет значение признака, не превосходящие указанного на оси абсцисс (рис.)

При помощи кумуляты изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.

При построении кумуляты интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а по оси ординат накопленные частоты которые наносят на поле графика в виде перпендикулярных линий на поле графика к оси абсцисс в верхних границах интервалов. Затем эти линии соединяют прямыми и получают ломаную линию – кумуляту (рис. 4.5).

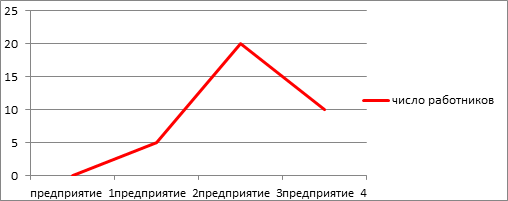
Рисунок 4.5. – Кумулята распределения работников на предприятиях отрасли

 

Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву.

Разновидностями линейной диаграммы являются: столбиковые диаграммы, полосовая (ленточная) диаграммы, кольцевые диаграммы, радиальные и круговые диаграммы и другие.

Рассмотрим правила построения столбиковой диаграммы, которая используется чаще всего для сравнения одноимённых показателей, характеризующих различные объекты или территории. Значения сравниваемых показателей изображаются при этом в виде вытянутых по вертикали прямоугольников.

При построении столбиковых диаграмм необходимо выполнять определенные требования: 1) шкала, по которой устанавливается высота столбиков, должна начинаться с нуля; 2) шкала должна быть, как правило, непрерывной; 3) основания столбиков должны быть равны между собой; 4) столбики могут быть размещены на одинаковом расстоянии друг от друга, вплотную один к другому или наплывом, при котором один столбик частично накладывается на другой; 5) наряду с разметкой шкалы соответствующими цифровыми надписями следует снабжать и сами столбцы.

Примером такой диаграммы служит рис 4.6.

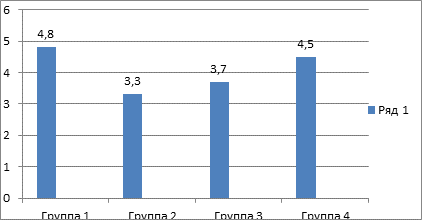
Рисунок. 4.6. Средняя оценка, полученная на экзамене по дисциплине «Статистика».

 

Разновидностью столбиковой диаграммы является полосовая (ленточная) диаграмма, для которой характерны горизонтальная ориентация столбиков (полос) и вертикальное расположение базовой линии. Полосовая диаграмма особенно удобна в тех случаях, когда отдельные объекты сравнения характеризуются противоположными по знаку показателями (рис. 4.7).

Рисунок. 4.7. Ленточная диаграмма

 

Иногда сравниваемые объекты характеризуются резко разнящимися значениями показателями. Например, численность населения Китая в 1986 г. составляла 1057, млн. чел, а Канады, имеющей немного большую площадь – 25,7 млн. чел. Представить эти данные с помощью столбиковой диаграммы практически невозможно, так как высота одного столбика должна в 41 раз превышать высоту другого (1057,2 = 25,7 + 41,1). В подобных случаях используют особые виды плоскостных диаграмм – квадратные или круговые. Их построение основано на том, что величины изображаемых показателей должны быть пропорциональны площадям квадратов или кругов, а корни квадратные из сравниваемых величин – линейным размерам этих фигур (сторонам квадратов или радиусам кругов), а затем построить квадраты со сторонами, пропорциональными полученным результатов.

Квадратные и круговые диаграммы, которые строятся аналогично. Данные виды диаграмм менее наглядны, чем столбиковые и полосовые, что связано с трудностью визуальной оценки соотношения площадей. Потому внутри квадратов и кругов следует поставить величины изображаемых показателей. Еще меньшей наглядностью отличаются объемные диаграммы (например, в виде кубов), в которых лимитные размеры графического образа пропорциональны корням кубическим из сравниваемых величин.

Диаграммы фигур-знаков представляют графические изображения в виде рисунков, силуэтов, фигур, соответствующих содержанию статистических данных. Они отличаются от других видов диаграмм тем, что отдельные величины на них изображаются отдельным количеством одинаковых по размеру и типу фигур.

Знак Варзара представляет собой прямоугольник, у которого один сомножитель принят за основание, другой – за высоту, а вся площадь равна их произведению.

Например, произведение площади торгового зала магазина и объема продаж. В прямоугольнике одну сторону брать пропорционально площади торгового зала, а другую объема продаж магазинов, то площадь прямоугольника и будет представлять знак Варзара, т. е. объем продаж магазина.

К формам структурных диаграмм относятся кольцевые диаграммы (рис. 4.8) и круговые диаграммы (рис. 4.9 и рис. 4.10). «Работающим» геометрическим параметром в секторной диаграмме удельных весов служит величина угла между радиусами: 1% принимается на диаграмме равным 3,6%, а сумма всех углов, составляющая 360˚, приравнивается к 100%. Поэтому круг разбивается на сектора пропорционально частям изображаемого целого.

Рисунок 4.8. Выручка российских оборонных комплексов в ТОП -100 за 2017 год (млрд. долл.)

Источник: Военно-промышленный курьер ВПК №49 (762)т 18-24 декабря 2018 года.

Или

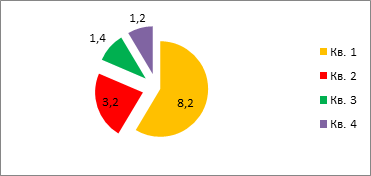
Рисунок 4.9. – Изменение ставки банковского кредита по кварталам года

 

Возможность применения секторных диаграмм ограничены двумя обстоятельствами. Первое заключается в том, что они сохраняют свою выразительность при делении совокупностей на небольшое число частей – не более 4-5, а за этими пределами их применение становится малоэффективным. Второе – секторная диаграмма выглядит убедительно лишь при существенных различиях сравниваемых структур, в противном случае она оказывается недостаточно выразительной.

Или круговая диаграмма (рис. 4.10).

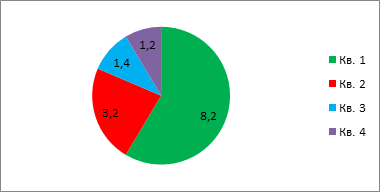
Рисунок 4.10. – Изменение ставки банковского кредита по кварталам года

 

Разновидностью линейной диаграммы является радиальная диаграмма, которая применяется для изображения рядов динамики при наличии в них сезонных колебаний. В качестве примера построения радиальной диаграммы возьмём следующее распределение:

месяцы	I	II	III	IV	V	VI	VII	VIII	ХIХ	Х	ХI	ХII
Уголь, т	50	62	64	74	63	90	61	63	69	57	57	54

Определим среднемесячную добычу угля, которая составляет 63,3. Рисуем круг радиусом среднемесячному показателю (R = 63,3 т в масштабе). На горизонтальном диаметре строим шкалу, взяв масштабную длину. Затем весь круг разделим на 12 радиусов (в соответствии с числом месяце в году). На радиусе делаем отметку согласно масштаба исходных данных за каждый месяц. Данные, которые превысили среднемесячную добычу отмечаются за пределами окружности на продолжении радиуса. Отметки различных месяцев соединяют между собой. Строится подобно лепестковые диаграммы рис. 4.11.

Другой формой структурных статистических диаграмм являются полосовые диаграммы удельных весов.

Эта диаграмма получена путем преобразования простой полосовой диаграммы с подразделенными полосами. Преобразование заключается в том, что ряды абсолютных показателей превращены в ряды относительных чисел – удельных весов.

Фигурные диаграммы сравнения предназначены в основном для целей популяризации. Показатели в них вычерчивают в виде определенного количества стандартных фигур, представляющих собой упрощенные изображения объектов характерных для соответствующих явлений. Недостатком их следует считать некоторую неточность, связанную с необходимостью округления изображаемых показателей.

Для изображения экономических явлений, протекающих во времени применяют динамические диаграммы. В отличие от диаграмм, отображающих сравнительные величины отдельных объектов или их структуры, в динамических диаграммах объектом отображения служат процессы.

К особым видам статистических графиков можно отнести следующие виды.

Номограммы, при помощи которых с достаточной для практики точностью получают решение уравнений, вычисляют значения функций нескольких аргументов и т.п. Номограммы удобны для графического изображения и применения уравнений множественной линейной регрессии.

Графическое изображение рядов распределения позволяет наглядно представить распределение данных статистического наблюдения.

Для отражения сезонных или циклических процессов, а также для наглядного отражения структурных сдвигов в изучаемых явлениях используются лепестковые диаграммы (диаграммы в системе полярных координат) (рисунок 4.11).

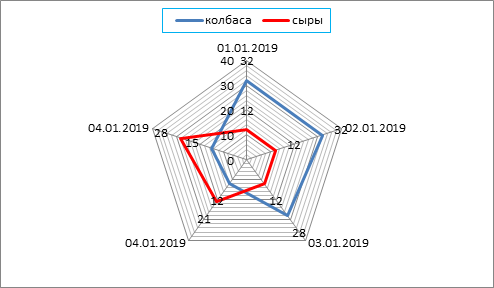
Рисунок 4.11. Изменение объема продаж в магазине №1 за первую неделю 2019 г.

 

Картограммы представляют собой географические карты, на которых при помощи графических образов нанесены показатели, характеризующие изучаемое явление. Они делятся на точечные и фоновые. При построении точечной картограммы графическим изображением статистических данных являются точки, размещенные в пределах территориальных единиц. На точечных картограммах величина изучаемого явления (например, поголовье скота) отражается при помощи точек, размер которых пропорционален величине данного явления. Точечные кардиограммы обычно служат для отражения количественных абсолютных показателей (численность сельского населения, поголовье скота валовой сбор урожая и т.д.).

Фоновая картограмма – это вид картограммы, на которой величина изучаемого показателя характеризуется либо штриховкой различного рода, либо окраской определенной степени насыщенности по отельной степени насыщенности по отдельным территориальным единицам. Фоновые картограммы обычно применяются для отображения средних или относительных показателей (средняя плотность населения, средний доход на душу населения и т.д.).

Картодиаграмма представляет собой сочетание диаграммы с географической картой. При этом элементы диаграммы (полосы, точки, круги, столбики, квадраты) располагаются на контуре географической карты, что дает возможность отражать территориальное размещение исследуемых показателей и их величину.

При построении графиков (диаграмм) в системе прямоугольных координат необходимо придерживаться следующих правил:

1. Каждый график должен иметь название, которое располагают под ним. В названии в краткой форме следует отразить содержание, место и время явления. Все графики нумеруются.

2. Оси координат должны быть названы и иметь единицы измерения.

3. На числовой оси следует откладывать только целые числа и в равном масштабе (например: 2; 4; 6 и т.д., или 10; 20; 30 и т.д.). Заканчиваться числовая ось должна той величиной, которая немногим больше максимальной величины в исходной совокупности.

4. Если на одной числовой оси необходимо расположить величины, относящиеся к одному и тому же явлению, но резко отличающиеся друг от друга по абсолютному значению, числовую ось можно разорвать знаком (≈), что означает разрыв масштаба.

5. Если необходимо отразить на одном графике (в одной системе прямоугольных координат) два-три явления, то вводят столько же дополнительных числовых осей (осей ординат). Каждая числовая ось должна иметь свою размерность и свой масштаб.

6. Если на графике характеризуется несколько явления, то обязательно должны быть представлены условные обозначения, располагаемые ниже поля графика.